Slide 1
... • If we do it classically we have to calculate f(x) many times. – It isn’t how easy it is to calculate f(x), it is how many times. – Need to go from 0 to N2 , this is a huge number of calculations for a 128 bit number! This could be 2(2*128) or ~1.16 x 1077 – The results have to be stored somewhere ...
... • If we do it classically we have to calculate f(x) many times. – It isn’t how easy it is to calculate f(x), it is how many times. – Need to go from 0 to N2 , this is a huge number of calculations for a 128 bit number! This could be 2(2*128) or ~1.16 x 1077 – The results have to be stored somewhere ...
Quantum computing with nanoscale infrastructure
... to try to beat nature on its home ground |01> or |10> or |11>. But the two-qubit register can be written as a|00>+b|01>+c|10>+d|11>. This means that the register is in all 22 =4 classical bit configurations at the same time! If we consider a register with 10 qubits, the number of possible simultaneo ...
... to try to beat nature on its home ground |01> or |10> or |11>. But the two-qubit register can be written as a|00>+b|01>+c|10>+d|11>. This means that the register is in all 22 =4 classical bit configurations at the same time! If we consider a register with 10 qubits, the number of possible simultaneo ...
Implementations of Quantum Information
... The Hamiltonian generates unitary evolution, which corresponds to dynamics in a closed system, but the system must be open for preparation and readout. The openness is the coupling of the system to the environment; e.g. a puck sliding on ice is slowed by frictional coupling to ice and air resist ...
... The Hamiltonian generates unitary evolution, which corresponds to dynamics in a closed system, but the system must be open for preparation and readout. The openness is the coupling of the system to the environment; e.g. a puck sliding on ice is slowed by frictional coupling to ice and air resist ...
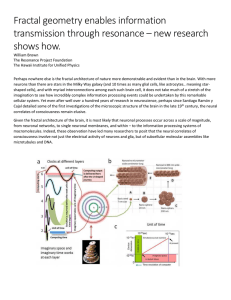
Fractal geometry enables information transmission through resonance
... extremely sensitive to even small changes, because of the nonlinear interactions that result from feedback operations and high global coherency within the system. As such, there is an indeterminate nature to fractal / chaotic systems, much like trying to predict the weather. So that in contrast to t ...
... extremely sensitive to even small changes, because of the nonlinear interactions that result from feedback operations and high global coherency within the system. As such, there is an indeterminate nature to fractal / chaotic systems, much like trying to predict the weather. So that in contrast to t ...
INTRODUCTION TO MECHANICS Introduction On the face of it
... the action allows us to describe the dynamics of a classical particle in a different manner in which the above example becomes very easy. 1.2. States, Observables, Measurement, and Dynamics. We begin with a question: given a path x(t) in Rn , how much information do we need to specify the motion of ...
... the action allows us to describe the dynamics of a classical particle in a different manner in which the above example becomes very easy. 1.2. States, Observables, Measurement, and Dynamics. We begin with a question: given a path x(t) in Rn , how much information do we need to specify the motion of ...
The Computer Science Picture of Reality
... Quantum algorithms and complexity theory explore fundamental questions with profound implications: • Quantum resistant cryptography. • Probabilistic method <--> quantum method Quantum complexity <--> classical complexity • quantum complexity theory <--> condensed matter physics • Verifying quantum c ...
... Quantum algorithms and complexity theory explore fundamental questions with profound implications: • Quantum resistant cryptography. • Probabilistic method <--> quantum method Quantum complexity <--> classical complexity • quantum complexity theory <--> condensed matter physics • Verifying quantum c ...
Questions for learning Quantum Mechanics of FYSA21
... 2. Solve the time independent Schrödinger equation in an infinitely deep one dimensional potential well located at 0 < x < a. Sketch the wavefunctions of the lowest-in-energy bound states. How do the bound state energies change when the width a is changed? (4p) 3. When there is a change in the poten ...
... 2. Solve the time independent Schrödinger equation in an infinitely deep one dimensional potential well located at 0 < x < a. Sketch the wavefunctions of the lowest-in-energy bound states. How do the bound state energies change when the width a is changed? (4p) 3. When there is a change in the poten ...
Ramsay_20_01_09
... Self-assembled quantum dots are nanoscale volumes of InGaAs embedded in a GaAs matrix. The dot provides electronic confinement in all three spatial dimensions, resulting in a set of discrete energy levels energetically isolated from their solid-state environment. This results in an atom-like coheren ...
... Self-assembled quantum dots are nanoscale volumes of InGaAs embedded in a GaAs matrix. The dot provides electronic confinement in all three spatial dimensions, resulting in a set of discrete energy levels energetically isolated from their solid-state environment. This results in an atom-like coheren ...