Ligand to Ligand Charge Transfer in
... transitions metals, the energies of metal d orbitals often lie between the highest occupied and lowest unoccupied ligand orbitals giving rise to ligand field, LMCT, and/or MLCT transitions lower in energy than LLCT. Further complicating the interpretation is metal-ligand covalency. Molecular orbital ...
... transitions metals, the energies of metal d orbitals often lie between the highest occupied and lowest unoccupied ligand orbitals giving rise to ligand field, LMCT, and/or MLCT transitions lower in energy than LLCT. Further complicating the interpretation is metal-ligand covalency. Molecular orbital ...
Quantum algorithms - People @ EECS at UC Berkeley
... Now let us look more closely at the quantum part of the algorithm. Some of the key quantum operations (which we will soon discuss) can be thought of as looking for certain kinds of patterns in a superposition of states. Because of this, it is helpful to think of the algorithm as having two stages. I ...
... Now let us look more closely at the quantum part of the algorithm. Some of the key quantum operations (which we will soon discuss) can be thought of as looking for certain kinds of patterns in a superposition of states. Because of this, it is helpful to think of the algorithm as having two stages. I ...
Experimental Test of Wave-Particle Duality by Single Neutral Atoms
... ticle behaviors. So far, all the experimental tests of BCP with single photons, as well as experiments with atoms [19], have suffered from limited detection efficiency, which implies that only some of the photons were registered and used to eventually evaluate the results. This makes the results les ...
... ticle behaviors. So far, all the experimental tests of BCP with single photons, as well as experiments with atoms [19], have suffered from limited detection efficiency, which implies that only some of the photons were registered and used to eventually evaluate the results. This makes the results les ...
Outline of section 5
... The integer m is known as the magnetic quantum number. It determines the z-component of angular momentum. For each value of l there are 2l+1 possible values of m. The simultaneous eigenfunctions of L2 and Lz do not correspond to definite values of Lx and Ly, because these operators do not commute wi ...
... The integer m is known as the magnetic quantum number. It determines the z-component of angular momentum. For each value of l there are 2l+1 possible values of m. The simultaneous eigenfunctions of L2 and Lz do not correspond to definite values of Lx and Ly, because these operators do not commute wi ...
L z
... The integer m is known as the magnetic quantum number. It determines the z-component of angular momentum. For each value of l there are 2l+1 possible values of m. The simultaneous eigenfunctions of L2 and Lz do not correspond to definite values of Lx and Ly, because these operators do not commute wi ...
... The integer m is known as the magnetic quantum number. It determines the z-component of angular momentum. For each value of l there are 2l+1 possible values of m. The simultaneous eigenfunctions of L2 and Lz do not correspond to definite values of Lx and Ly, because these operators do not commute wi ...
Anyons and the quantum Hall effect— A pedagogical
... satisfy Schroedinger’s wave equation. And second, these wave functions should satisfy certain symmetry properties with respect to the exchange of identical particles. For fermions the wave function should be anti-symmetric, for bosons it should be symmetric. It is impossible to overrate the importan ...
... satisfy Schroedinger’s wave equation. And second, these wave functions should satisfy certain symmetry properties with respect to the exchange of identical particles. For fermions the wave function should be anti-symmetric, for bosons it should be symmetric. It is impossible to overrate the importan ...
QUANTUM MONTE CARLO SIMULATION OF TUNNELLING DEVICES USING WAVEPACKETS AND BOHM TRAJECTORIES
... I have read somewhere that science has to be considered as a type of culture at the same level as painting, playing music or writing poetry. It indicates the human development of the society. However, science is also an economical motor of our society because its has a direct impact on our everyday ...
... I have read somewhere that science has to be considered as a type of culture at the same level as painting, playing music or writing poetry. It indicates the human development of the society. However, science is also an economical motor of our society because its has a direct impact on our everyday ...
Quantum Monte Carlo simulations of solids W. M. C. Foulkes
... provide are often difficult or impossible to obtain in any other way. In studying the quantum-mechanical properties of solids, we are fortunate that the underlying physical laws have been known for over 70 years. The difficulty arises from the complexity of the equations that, as Dirac (1929) famous ...
... provide are often difficult or impossible to obtain in any other way. In studying the quantum-mechanical properties of solids, we are fortunate that the underlying physical laws have been known for over 70 years. The difficulty arises from the complexity of the equations that, as Dirac (1929) famous ...
Chapter 28: Quantum Physics
... orbit the nucleus. Quantum mechanics can be used to determine the allowed energy levels and wave functions for the electrons. ...
... orbit the nucleus. Quantum mechanics can be used to determine the allowed energy levels and wave functions for the electrons. ...
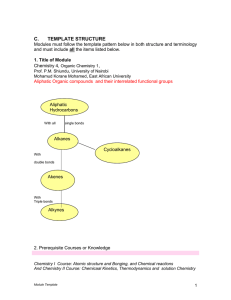
2.6 M - Thierry Karsenti
... atoms in the cyclic structure is other than carbon. Heterocyclic componds may be aliphatic or aromatic 15. Isomers: These are different compounds that have the same molecular formula. Isomers are further subdivided into: (a) structural isomers, (b) geometrical isomers and (c) stereoisomers(optical i ...
... atoms in the cyclic structure is other than carbon. Heterocyclic componds may be aliphatic or aromatic 15. Isomers: These are different compounds that have the same molecular formula. Isomers are further subdivided into: (a) structural isomers, (b) geometrical isomers and (c) stereoisomers(optical i ...
Power Point over chemistry
... retaining heat is important to our climate. It means that our climate stays much more stable than it would if there were less water on Earth. TAKS Need to Know ...
... retaining heat is important to our climate. It means that our climate stays much more stable than it would if there were less water on Earth. TAKS Need to Know ...
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term may also refer to the physical region or space where the electron can be calculated to be present, as defined by the particular mathematical form of the orbital.Each orbital in an atom is characterized by a unique set of values of the three quantum numbers n, ℓ, and m, which respectively correspond to the electron's energy, angular momentum, and an angular momentum vector component (the magnetic quantum number). Any orbital can be occupied by a maximum of two electrons, each with its own spin quantum number. The simple names s orbital, p orbital, d orbital and f orbital refer to orbitals with angular momentum quantum number ℓ = 0, 1, 2 and 3 respectively. These names, together with the value of n, are used to describe the electron configurations of atoms. They are derived from the description by early spectroscopists of certain series of alkali metal spectroscopic lines as sharp, principal, diffuse, and fundamental. Orbitals for ℓ > 3 continue alphabetically, omitting j (g, h, i, k, …).Atomic orbitals are the basic building blocks of the atomic orbital model (alternatively known as the electron cloud or wave mechanics model), a modern framework for visualizing the submicroscopic behavior of electrons in matter. In this model the electron cloud of a multi-electron atom may be seen as being built up (in approximation) in an electron configuration that is a product of simpler hydrogen-like atomic orbitals. The repeating periodicity of the blocks of 2, 6, 10, and 14 elements within sections of the periodic table arises naturally from the total number of electrons that occupy a complete set of s, p, d and f atomic orbitals, respectively.