Quantum Condensed Matter Field Theory
... formal exact solution is at hand. Such misconceptions are often reinforced by the allure of sophisticated analytical machinery developed in courses devoted to mathematical methods. However, the limitations of a ‘first-principles’ or ‘microscopic approach’ is nowhere more exposed than in the study of ...
... formal exact solution is at hand. Such misconceptions are often reinforced by the allure of sophisticated analytical machinery developed in courses devoted to mathematical methods. However, the limitations of a ‘first-principles’ or ‘microscopic approach’ is nowhere more exposed than in the study of ...
Quantum Mechanics
... ULTIMATE REALITY? Quantum fields fill all space; one field for each kind of particle. Particles are just localized bunches of energy carried by the fields. Particles can appear and disappear spontaneously from the fields. Perhaps the universe appeared in just this way. ...
... ULTIMATE REALITY? Quantum fields fill all space; one field for each kind of particle. Particles are just localized bunches of energy carried by the fields. Particles can appear and disappear spontaneously from the fields. Perhaps the universe appeared in just this way. ...
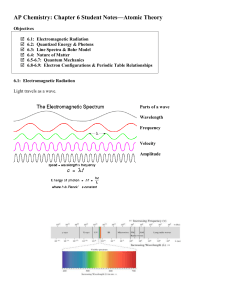
Ch. 6 notes
... 6.5-6.7: Quantum Mechanics Developed by Werner Heisenberg (1901-1976), Louis De Broglie (1892-1987), Erwin Schrodinger (1887-1961) This answers the question: Where is the _____________ in the atom? The answer is complex. We can’t say exactly where the atom is. We can only say where we think it _____ ...
... 6.5-6.7: Quantum Mechanics Developed by Werner Heisenberg (1901-1976), Louis De Broglie (1892-1987), Erwin Schrodinger (1887-1961) This answers the question: Where is the _____________ in the atom? The answer is complex. We can’t say exactly where the atom is. We can only say where we think it _____ ...
Lectuer 15
... - The third quantum number m is called the magnetic quantum number - It takes on the 2 Ɩ + 1 values m = 0, ±1, ±2, ……, ± Ɩ. - The z component of the angular momentum is determined completely by m through L z = m ħ. - The quantum number m is called the magnetic quantum number because the energy of a ...
... - The third quantum number m is called the magnetic quantum number - It takes on the 2 Ɩ + 1 values m = 0, ±1, ±2, ……, ± Ɩ. - The z component of the angular momentum is determined completely by m through L z = m ħ. - The quantum number m is called the magnetic quantum number because the energy of a ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 12. Derive the time-independent Schroedinger equation from the time-dependent equation. 13. What is a hermitian operator? Show that the wave functions corresponding to two different eigen values of a Hermitian operator are orthogonal. 14. Write the Schroedinger equation for 1-D harmonic oscillator. ...
... 12. Derive the time-independent Schroedinger equation from the time-dependent equation. 13. What is a hermitian operator? Show that the wave functions corresponding to two different eigen values of a Hermitian operator are orthogonal. 14. Write the Schroedinger equation for 1-D harmonic oscillator. ...
Homework 8
... 1) A particle of mass m can slide freely along a wire AB whose perpendicular distance to the origin O is h. The line OC rotates about the origin at constant angular velocity . The position of the particle can be described in terms of the angle and distance q to the point C. If the particle i ...
... 1) A particle of mass m can slide freely along a wire AB whose perpendicular distance to the origin O is h. The line OC rotates about the origin at constant angular velocity . The position of the particle can be described in terms of the angle and distance q to the point C. If the particle i ...
Lecture 14
... The energy level diagram starts at -13.6 eV, which is the binding energy of the ground state n = 1, and continues with -3.4 eV, which is the binding energy of the first excited state, and so on. [[DIAGRAM]] There are also states at positive energies. They correspond to wavefunctions that are not bou ...
... The energy level diagram starts at -13.6 eV, which is the binding energy of the ground state n = 1, and continues with -3.4 eV, which is the binding energy of the first excited state, and so on. [[DIAGRAM]] There are also states at positive energies. They correspond to wavefunctions that are not bou ...
preprint
... has spectrum bounded from below. In other words, we assume that there is a lower bound on energy. Suppose now for reductio ad absurdum that for any interval (a, b) of real numbers, there is a subspace s(a, b) of states that come about during that interval. Let e(a, b) to represent the projection on ...
... has spectrum bounded from below. In other words, we assume that there is a lower bound on energy. Suppose now for reductio ad absurdum that for any interval (a, b) of real numbers, there is a subspace s(a, b) of states that come about during that interval. Let e(a, b) to represent the projection on ...
Notes on - Paradigm Shift Now
... geometry (10). At the same time it must be pointed out that the supposedly unsatisfactory non local features of the Quantum potential Q become meaningful in the above context at the Compton scale, within which indeed we have exactly such non local effects [13]. It may be pointed out that more recent ...
... geometry (10). At the same time it must be pointed out that the supposedly unsatisfactory non local features of the Quantum potential Q become meaningful in the above context at the Compton scale, within which indeed we have exactly such non local effects [13]. It may be pointed out that more recent ...
Document
... the parameter that gives the infinitesimal change is a vector field. Hence these constraints must multiply a vector field, without using a metric. Thus these constraints are the components of a one form. It should also be invariant under ordinary gauge transformations, as they commute with differomo ...
... the parameter that gives the infinitesimal change is a vector field. Hence these constraints must multiply a vector field, without using a metric. Thus these constraints are the components of a one form. It should also be invariant under ordinary gauge transformations, as they commute with differomo ...
Link between the hierarchy of fractional quantum Hall states and
... Link between the hierarchy of fractional quantum Hall states and Haldane’s conjecture for quantum spin chains Masaaki Nakamura Department of Physics, Tokyo Institute of Technology, Tokyo 152-8551, Japan ...
... Link between the hierarchy of fractional quantum Hall states and Haldane’s conjecture for quantum spin chains Masaaki Nakamura Department of Physics, Tokyo Institute of Technology, Tokyo 152-8551, Japan ...