Download Convection Principles

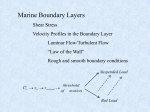
1
7. PRINCIPLES OF CONVECTION
Objective is to determine h values for the combinations of:
› Different geometric configurations
» internal flow
» external flow (flat plates, cylindrical & spherical bundles)
› Types of fluid flow
» laminar flow
» turbulent flow
› Types of convection
» forced convection
» natural convection
1. Introduction
- Definitions
q"  h(Ts  T )
where, h = LOCAL heat transfer coefficient
› Again, we have used an average h defined as:
h  1  h dAs
As A
s
› Thus, the heat flux varies locally and the total heat flux is:
q   q" dAs   h(Ts  T ) dAs h As (Ts  T )
As
As
2. Boundary Layer Concept
2
- Velocity Boundary Layer
› Shear stress  causes the retardation of flow from the wall to
some point where velocity is almost that of free stream (u)
   du
dy
At the plate surface, us = 0 (i.e., nonslip surface)
› Velocity BL thickness, 
The distance from the wall to a point where u( y)  0.99u
- Thermal Boundary Layer
› The thermal BL develops because of the temperature
difference between the free stream and the plate wall
› Thermal BL thickness, t
The distance from the wall to a point where T ( y)  0.99T
› At the surface, heat flux must obey Fourier’s Law:
q"s  k dT
dy
y 0
Coupling with convection rate equation q"s  h(Ts  T ) , h
can be calculated by:
k
dT
h
(Ts  T ) dy y  0
3
- Laminar vs Turbulent Flow
› For a flat plate:
u  x

u x
Critical Reynold Number: Re c   c ~ 5 x105

› For a tube:
Reynold Number:
Re 
u D
 2000 to 4000

3. Boundary Layer Equations
- Continuity Equation (Mass Conservation)
Re c 
4
Mass conservation:  m
 in   m
 out  m
 st
Then,




(u )dy  (v)dx  u   (u )dx dy  v   (v)dy  dx   (dxdy)
x
y
t


After simplification,
 (u )   (v)   
x
y
t
- Momentum Equation
Goal is to apply Newton’s second law:
 Fx 
d (mV ) x
dt
Need to consider:
› Body forces:
gravitational, magnetic, electrical, etc.
› Surface forces: normal and shear
Basic Assumptions
› Steady-state, incompressible fluid
›  = const.
› P  0 and   0
y
x
5
Inflow of momentum =
(udy)u  (vdx)u
Outflow of momentum =
[(u )u ] 
[(v)u ] 


(u )u  x dxdy  (v)u  y dy dx




Net pressure force =

Pdy  Pdy  P dxdy
x

Net viscous force =
 


 u dx   u    u dy  dx
y
 y y x 
Substitute into Newton’s law and simplify
2


 u u  v u    dP    u2
y 
dx
 x
y
Net momentum
normal force
- Energy Equation
Basic Assumptions
› Steady-state, incompressible fluid
› Constant , k, cp
shear force
6
Energy balance equation is
E k , x  E k , x  dx  E k , y  E k , y  dy  E h, x  E h, x  dx  E h, y  E h, y  dy  W  E g
Note that the work done by viscous force, W
› At the bottom:
› At the top:
 u 
  dx u
 y 
 (u  u / ydy)   u 
dx  u  dy 

y
y 

Substitute into the energy balance equation and simplify after
neglecting the second-order differentials:
2
2
2

T

T
k
d
T
k
d
T    u   q
u
v


 
x
y c p dy 2 c p dx 2 c p  y 
2
2
k
d
T
d
T

Note that  
and
c p
dy 2
dx 2
The above equation becomes
2
u T  v T   d T2  q
x
y
dy
For the cases with no heat generation
2
u T  v T   d T2
x
y
dy
- Mass Equation
Assumptions:
› SS
› No reactions
By analogy, we can write:
C A
C A
d 2C A
u
v
 D AB
x
y
dy 2
7
4. Solutions to BL Equations
Mass:
Momentum:
u  v  0
x y
2
p


 u u  v u       u
y 
x
 x
y 2
2
u T  v T   d T
x
y
dy 2
Energy:
- Analytical Solution
› Assumptions
» Laminar flow over a flat plate
» Steady-state, incompressible fluid
» Constant fluid properties
» Negligible viscous dissipation
› Blasius Solution to Momentum Equation
» Noting the momentum equation is independent of
temperature, we can define a stream velocity function :
and
v   
u  
y
x
to satisfy the continuity equation.
» Boundary layer similarity gives:
u  ( y )
u

» Order-of-magnitude analysis leads to:
~

x
u x
8
» Define the similarity variable
  y u  / x
Holding x constant,
   udy   u ()
dy
d  u x  ()d  u x f ()
d
» Write u, v and their derivatives
f u
f

u    
 u x
 u
y  y
 x

2
Similarly, we can write v, u , u ,  u
x y y 2
» Substitute
equation:
these
d2 f
2 3  f  2
d
 d
d3 f
expressions
into

0


with boundary conditions:
u ( x,0)  v( x,0)  0 , and
in terms of :
f
and
 f (0)  0
 0
» Velocity BL solution
f
f’

u( x, )  u
f
1
 
f”
0
0.4
0
0.027
0
0.133
0.332
0.331
4.8
5.2
3.085
3.482
0.988
0.994
0.039
0.022
» BL thickness
At f '  u / u   0.99 ,   5.0
   yu  0.99u  5.0  5.0 x

u / x
Re x
(Eqs. 7.13 to 16)
the
momentum
9
» Shear stress at the surface
 s   u
y
y 0
 u
u  2 f
x 2
 0.332u
 0
u
x
The local friction coefficient is
C f ,x 
s
0.664

Re x
u 2 / 2
› Pohlhausen Solution to Energy Equation
» Define the dimensionless parameters

T  Ts
T  Ts
» Assume the similarity function as
  ()
» Substitute into the energy equation and simplify
d 2   Pr f d  0
d 2 2 d
with boundary conditions:
and
(0)  0
()  1
where: Pr   /  (control the relation between the velocity
and temperature distribution)
Solve numerically (Pr  0.6)
 /    0  0.332(Pr)1 / 3
» Local heat transfer coefficient, hx
hx 
k
dT
(Ts  T ) dy

y 0
 k (T  Ts ) dθ dη
u
 k  dθ
(Ts  T ) dη dy   0
x dη   0
 Nu x  hx x  0.332(Re)1/ 2 (Pr)1/ 3
k
where:
Nux = Nusselt No.
Pr  0.6
10
› Average friction and heat transfer coefficients, ( C f , L , hL )
» Average friction coefficient
C f , L  1 0L C f , x dx  1.328
L
Re L
» Average friction coefficient
hx L L 1 L
1/ 2
1/ 3

0 hx dx  0.664(Re L ) (Pr)
k
kL
Pr  0.6
- Mass Convection in Laminar Flow
› Local Mass Transfer Coefficient
By analogy
Shx 
where:
hm x
 0.332(Re)1 / 2 ( Sc)1 / 3
D AB
Shx = Sherwood No.
Sc = Schmidt No. (   )
D AB
› Average Mass Transfer Coefficient
ShL 
hm L
 0.664(Re L )1 / 2 ( Sc)1 / 3
D AB
- Dimensional Analysis
Assume the dimensionless variables:
y
L
x*  x
L
y* 
u*  u
V
T  Ts
T* 
T  Ts
v*  v
V
C *A 
C A  C A, s
C A,   C A, s
p* 
p
V 2
11
Substitute into the BL equations and simplify (see Table 6.1):
u *  v *  0
Mass:
x *
y *
Momentum:
*
*
2 *
p *
* u

u
1

u
u
v
 * 
*
*
Re L *2
x
y
x
y
Energy:
*
*
2 *
u * T *  v * T *  1 d T2
Re L Pr *
x
y
dy
*
Concentration:
u
*
C *A
x *
v
*
C *A
y *

1
d 2 C *A
Re L Sc
dy *
2
› Velocity
From the above dimensionless momentum equation
 * *
p * 

u  f1  x , y , Re L , * 
x 

*
The shear stress at the surface:
 s   u
y
y 0
 V  u *


 L  y *
y* 0
From the coefficient of friction, we can write:
s
 2  u *
Cf 



V 2 / 2  Re L  y *
y* 0
 *
p * 

 f 2 x , Re L , *

x 

Since p*(x*) is related to the surface geometry, it can be
written as:

C f  f 2 x * , Re L

Integrating over the length L, x*/L = 1. Thus,
C f  f 2 Re L 
 Friction coefficient is only a function of Reynolds
Number in laminar flow conditions!
12
› Heat and Mass Transfer Coefficients (See Table 6.3)
- Reynolds Analogy
› dp*/dx* = 0 and Pr = Sc = 1
Basic BL equations along with their boundary conditions
are of exactly same form. So are their solutions.
Re L
 Cf
 Nu  Sh
2
Define the Stanton Numbers are:

k  Nu
Heat transfer: St  h  hL
u c p
k u L c p  Re Pr
hm hm L  DAB

 Sh
u DAB u L 
Re Sc
The above equation can be written as:
Mass transfer: Stm 
13
Cf
 St  St m
2
› dp*/dx* = 0 only
Use the laminar flow on a flat plate as an example & recall:
C f  0.664 Re 1 / 2
Nu  0.332(Re)1 / 2 (Pr)1 / 3
Combine these two equations:
Cf
(Pr)2 / 3
1
1 / 3
 2(Re) (Pr)
2
Nu
Re Pr
Cf
 St Pr 2 / 3  jH

2
By analogy, the Reynolds analogy for mass transfer is:
Cf
 Stm Sc 2 / 3  jm
2
where: jH and jm = Colburn j factors for heat and mass
5. Turbulent Flow
- Turbulent Boundary Layer
P  P  P'
where:
P  u, v, T , C A
› Steady-state is defined as P is independent of time
› Due to their random fluctuating nature, it is impossible to
predict the exact variation with time
14
- Turbulent Equations
Due to the fluctuating nature, BL equations must be modified!
Momentum:




 u u  v u    dP     u  u 'v' 
y 
dx y  y
 x

Energy:


u T  v T  1 d  k T  c p v'T ' 
x
y c p dy  y

Concentration:
u
C A
C
C A


 v A  d  D AB
 v' C A ' 
x
y
dy 
y

- Definition of Eddy Diffusivity
Momentum:
 u ' v'   M u
Energy:
Concentration:
y
 v'T '   H T
y
C A
 v' C A '   m
y
Thus,
Total shear stress:
Total heat transfer:
Total mass transfer:
tot  (v   M ) u
y
q"tot  c p (   H ) T
y
C
N "A, tot  ( D AB   m ) A
y
Note: Eddy diffusivities in turbulent core as much as 100 times
larger than molecular counterparts