Download Sec. 4.2 Congruent Triangles

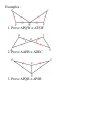
Sec. 4.1 Triangles and Angles
Triangle – a figure formed by three segments joining
three non-collinear points.
vertex – each of the three points joining the sides
adjacent sides – two sides sharing a common vertex
legs – sides that form the right angle in a right triangle
hypotenuse – side opposite the right angle in a right
triangle
legs (in an isosceles triangle) – two congruent sides in
an isosceles triangle with only two sides congruent
base – side that is not congruent to the two congruent
sides in an isosceles triangle.
interior angles – the three original angles in a triangle.
exterior angles – When the sides of a triangle are
extended, angles are formed. The angles adjacent to the
interior angles are exterior.
Thm. 4.1 Triangle Sum Theorem
The sum of the measures of the interior angles of a
triangle is 180.
Thm. 4.2 Exterior Angle Theorem
The measure of the exterior angle of a triangle is
equal to the sum of the measures of the two nonadjacent
interior angles.
corollary to a theorem – a statement that can be
proved easily using a theorem.
Corollary to the triangle sum theorem :
The acute angles of a right triangle are
complementary.
Sec. 4.2 Congruent Triangles
Congruent figures have exactly the same shape and
size.
Corresponding angles – angles that match up with
each other from one figure to the next. Corresponding
angles must be congruent in congruent figures.
Corresponding Sides – sides that match up with each
other from one figure to the next. Corresponding sides
must be congruent in congruent figures.
Thm. 4.3 Third Angle Theorem
If two angles of one triangle are congruent to two
angles of another triangle, then their third angles are
congruent.
Examples
1. Name all of the congruent sides.
2. Name all of the congruent angles.
NPLM  EFGH
3. Find x.
4. Find y.
5. Find x.
6. Find mM.
Sec. 4.3 Proving Triangles Congruent : SSS and SAS
Q : How much do you need to know about two triangles
to prove that they are congruent? Do you need to know
that all corresponding sides are congruent and all
corresponding angles are congruent in order to prove
that the triangles are congruent?
We have several theorems and postulates we use to
prove triangles are congruent.
Post. 19 : Side–Side–Side (SSS) Congruence Postulate
If three sides of one triangle are congruent to three
sides of another triangle, then the two triangles are
congruent.
Once you prove the triangles are congruent using SSS,
then you can state that the corresponding angles are
congruent by ‘Corresponding Parts of Congruent
Triangles Are Congruent’ or CPCTC.
Post. 20 : Side-Angle-Side (SAS) Congruence Postulate
If two sides and their included angle of one triangle
are congruent to two sides and their included angle of
another triangle, then the triangles are congruent by
SAS.
Once you prove the triangles are congruent using SAS,
then you can state that the third pair of corresponding
sides and the other two pairs of corresponding angles
are congruent by CPCTC.
***When proving triangles congruent, always look for
shared sides and vertical angles. Shared sides and
vertical angles are automatically congruent because of
reflexive property and the “vertical angles are
congruent” theorem.
Examples :
1. Prove PQW  TSW
2. Prove AEB  DEC
3. Prove PQR  PSR
Sec. 4.4 Proving Triangles are Congruent : AAS and
ASA
Post. 21 : Angle-Side-Angle (ASA) Congruence Post.
If two angles and the included side of one triangle
are congruent to two angles and the included side of a
second triangle, then the triangles are congruent.
Thm. 4.5 Angle-Angle-Side (AAS) Congruence Thm.
If two angles and a non-included side of one
triangle are congruent to two angles and a non-included
side of another triangle, then the triangles are
congruent.
Examples :
Is it possible to prove the triangles congruent? If so,
state the thm. or post. and write the congruence.
Given : AD || EC ; BD  BC
Prove : ABD  EBC
Sec. 4.6 Isosceles, Equilateral, and Right Triangles
base angles – two angles adjacent to the base in an
isosceles triangles
vertex angle – angle included by the two legs
Thm. 4.6 Base angles theorem
If two sides of a triangle are congruent, then the
angles opposite those sides are also congruent.
Thm. 4.7 Converse of the base angles theorem
If two angles of a triangle are congruent, then the
sides opposite those angles are also congruent.
Corollary to Thm. 4.6
An equilateral triangle is also equiangular.
Corollary to Thm. 4.7
An equiangular triangle is also equilateral.
Thm. 4.8 Hypotenuse-Leg (HL) Congruence Thm.
If the hypotenuse and leg of one right triangle are
congruent to the hypotenuse and leg of another right
triangle, then the triangles are congruent.