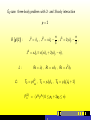Download Lie Algebras and the Schr¨odinger equation: (quasi-exact-solvability, symmetric coordinates) Alexander Turbiner

Lie Algebras and the Schrödinger equation:
(quasi-exact-solvability, symmetric coordinates)
Alexander Turbiner
Nuclear Science Institute, UNAM, Mexico
September 18, 2010
Let us consider the Hamiltonian = the Schrödinger operator
H = −∆ + V (x) ,
x ∈ Rd
A problem of quantum mechanics is to solve the Schrödinger
equation
HΨ(x) = E Ψ(x)
,
Ψ(x) ∈ L2 (R d )
finding the spectra (the energies and eigenfunctions).
The Hamiltonian is an infinite-dimensional matrix
To solve the Schrödinger equation ⇒ diagonalize the
infinite-dimensional matrix
It is transcendental problem, the characteristic polynomial is of
infinite order and it has infinitely-many roots.
One-dimensional Anharmonic Oscillator
H = −
d2
+ m2 x 2 + gx 4
dx 2
Ground State Energy E0 (m2 , 1)
(m2 ⇒
m2
,g
g 1/3
⇒ 1)
m2
Infinitely-many square-root branch points
(level crossings, Bender-Wu ’69, Gabrielov-Eremenko ’09)
⇛ Infinitely-sheeted Riemann surface on E in m2
Studying one eigenstate implies a study of the whole spectra
(via analytic continuation)
Do exist Hamiltonians H with algebraic substructure
det(H − E ) = det(H − E )n×n det(H − E )∞−n×∞−n
(factorization)
It implies the existence of the basis where matrix H has
block-diagonal (block-triangular) form.
Factorization does not depend on basis! (invariant property)
How to find it (if exist)?
Example 1:
x4
Take Ψ0 = e −a 4
- ground state (no nodes)
Find a potential for which it’s the lowest eigenfunction
′′
V0 =
Ψ0
Ψ0
= a2 x 6 − 3ax 2 and E0 = 0
Define
H0 = −∂x2 + a2 x 6 − 3ax 2
where one eigenstate is known exactly ⇛
det(H0 − E ) = E det(H0 − E ){∞−1}×{∞−1}
V(x)= −3x 2 + x 4
2
−1
1
x
−2
Figure: The double-well potential V = a2 x 6 − 3ax 2 (at a = 1) with
x4
Ψ0 = e −a 4 and E0 = 0
Example 2:
√
x4
Take Ψ± = ( 2ax 2 ± 1)e −a 4
(+) ground state (no nodes) and
(−) 2nd excited state (two nodes)
There is a potential(!) for which Ψ± are the eigenfunctions
′′
√
Ψ±
2 6
2
Ψ± = a x − 7ax and E± = ∓2 2a
Define
H1 = −∂x2 + a2 x 6 − 7ax 2
where two eigenstates are known exactly (either Ψ± or E± form
two-sheeted Riemann surface in a), ⇛
det(H1 − E ) = (E 2 − 8a) det(H1 − E ){∞−2}×{∞−2}
Example n:
x4
Take Ψn = Pn (x 2 )e −a 4
– Pn (x 2 ) is a set of (n + 1)
polynomials having from zero up to 2n nodes
There is a single potential(!) in which all Ψn are the eigenfunctions
′′
Ψn
= a2 x 6 − (4n + 3)ax 2 , Qn+1 (E , a) = 0 ,
Ψn
where Qn+1 (E , a) is (n + 1)th degree polynomial in E with real
roots at a > 0
Define
Hn = −∂x2 + a2 x 6 − (4n + 3)ax 2
where (n + 1) eigenstates are known exactly (algebraically) (either
Ψn or En form (n + 1)-sheeted Riemann surface in a), ⇛
det(Hn − E ) = Qn+1 (E , a) det(Hn − E ){∞−n−1}×{∞−n−1}
Vn,p = a2 x 6 + 2abx 4 + [b 2 − (4n + 2p + 3)a]x 2 , p = 0, 1
the unique polynomial 1D quasi-exactly-solvable potential
with three possible patterns: single-well, double-well, triple-well
Eigenfunctions:
x4
Ψn,p = x p Pn (x 2 )e −a 4 −b
x2
2
What is behind quasi-exact-solvability?
Lets us make a gauge rotation of the Hamiltonian Hn with Ψ0,p
and introduce new variable t = bx 2 :
hn (t, ∂t ) ≡
1
2
4
2
4
(x p e −bx /2−ax /4 )−1 Hn (x p e −bx /2−ax /4 ) |t=bx 2
4b
1
= −t∂t2 + (at 2 + t − p − )∂t − ant ,
2
It’s Algebraic form of Hn .
⋆ hn has finite-dimensional invariant subspace
Pn =< 1, t, t 2 , . . . t n >
⋆ hence, it has (n + 1) polynomial eigenfunctions:
(k)
Pn (t) =
n
X
(k)
γi t i , k = 0, 1, . . . , n ,
i =0
Does Pn have a Lie-algebraic meaning? – It does!
gl2 -algebra (in R)
∂
∂t
∂
J0 = t
∂t
∂
Tn0 = t
− n
∂t
∂
= tTn0 = t(t
− n)
∂t
J− =
Jn+
⋆ Pn is finite-dimensional irreducible representation space of
dimension (n + 1)
⋆ Generators Jn+ , J − and Tn0 + J 0 span the algebra sl (2)
⋆ Pn form the infinite flag
P0 ⊂ P1 ⊂ P2 ⊂ . . . ⊂ Pn ⊂ . . . P
gl (2)-representation
1
hn (t, ∂t ) = aJn+ − J 0 J − + J 0 − (p + )J −
2
⋆ (degenerate) Quantum top in constant magnetic field
⋆ # of known eigenstates ≡ dimension of finite-dimensional
irreducible representation
⋆ Finite-dimensional invariant subspace Pn of hn (t, ∂t ) ≡
finite-dimensional irreducible representation space of gl (2)
Quasi-exactly-solvable Hamiltonian Hn has a hidden Lie
algebra gl (2),
it implies it can be rewritten in terms of gl (2) generators.
It is well-seen in the space t = x 2 , where Z 2 -symmetry of the
problem realized!
What would happen if a = 0 (highest-weight generator is absent)?
⋆ hn (t, ∂t ) has infinitely-many finite-dimensional invariant
subspaces Pn , n = 0, 1, 2, 3, . . ..
⋆ It preserves the flag ⇒ it implies block-diagonal structure of Hn
⇒ complete factorization of the characteristic equation to product
of monomials and, ⇒ exact-solvability
1
hexact = −t∂t2 + (t − p − )∂t =
2
1
2
2
(x p e −bx /2 )−1 Hexact (x p e −bx /2 ) |t=bx 2
4b
Hexact = −∂x2 + b 2 x 2
We recover the harmonic oscillator!
1
hexact (t, ∂t ) = − J 0 J − + J 0 − (p + )J −
2
It is the gl (2)-Lie-algebraic form in generators of b ⊂ gl (2).
This Lie-algebraic form is different from the second-quantization
form
Hexact = {a+ a}
They act in different spaces, Hexact is generator of gl (2), hexact is
non-linear combination of generators as well as hn ....
How to find such a basis in general, if exists?
theory comes to mind!
-
representation
Take
hn =
X
α,β=±,0
aαβ Jα Jβ +
X
α=±,0
bα J α
It has (n + 1)-finite-dimensional invariant subspace by construction
hexact =
X
α,β=−,0
aαβ Jα Jβ +
X
α=−,0
bα J α
It has infinitely-many, finite-dimensional invariant subspaces by
construction
Substitute Jα in explicit form
hn = Q4 (t)∂t2 + Q3 (t)∂t + Q2 (t)
where Q4,3,2 are polynomials of degree 4,3,2. It is Heun operator.
⋆ To Schrödinger form:
change of variable t = t(x) and make gauge rotation g −1 hn g .
Finally,
g −1 hn g |t=t(x) = −∂x2 + V (x)
where x =
R
√ dt
Q4 (t)
– elliptic change of variable
CLASSFICATION
⋆ All four known 1D exactly solvable problems (Harmonic
Oscillator, Coulomb Problem, Morse Potential and Pöschle-Teller
Potential) have gl (2) hidden algebra
⋆ There exist 11 gl (2)-Lie-algebraic Potentials
◮
◮
◮
One polynomial QES Potential in (−∞, ∞)
One finite-piece Laurant series (in r ) QES Potential in [0, ∞)
Two QES Coulomb Potentials
◮
Three QES Morse Potentials
◮
Two QES Pöschl-Teller Potentials
◮
One QES Mathieu Potential (Magnus-Winkler Potential)
◮
(generalized)Lame Potential
It exhausts all 1D Schrödinger eqs having reduced to polynomial
eigenfunctions.
Is there anything else, beyond Lie algebras?
⋆ Yes! (1995, 2009) Eigenfunctions are from
P̃n =< 1, t, t 2 , . . . , t n−2 , t n >
(one monomial is missing)
⋆ Quantum algebra sl (2)q (in Azbel-Hofstadter Hamiltonian
(Wiegmann-Zabrodin, ’95))
Is there anything else with gl (2), perhaps, beyond differential operators?
Let us make a quantum canonical transformation of quantum
phase space.
Three (minimal) realizations of h3 : [a, b] = 1, a|0i = 0
d ,
∗ a = dt
b=t
d
∗ aδ = D+δ , bδ = tδ ≡ t (1 − δD−δ ) = te −δ dt
∗ aq = Dq ,
bq = tq ≡ (q − 1)t
1+t
d
q 1+t dt
d
dt
−1
f (t ± δ) − f (t)
where D±δ f (t) =
and Dq f (t) =
±δ
discrete or Jackson derivative.

(I ) 









(II ) 










(III ) 
|0i = 1
f (qt)−f (t)
t(q−1) ,
(I) ”coordinate-momentum” representation
(II) is due to Yu.F. Smirnov and A.T. ’95 (uniform lattice)
(III) is due to C. Chryssomalakos and A.T. ’01 (exponential lattice)


t k+1
(I )







k+1
(II )
t (k+1)
Basic object : b
|0i =







 (k+1)! t k+1
(III )
{k+1}!
where t (k+1) ≡ t(t − δ) · · · (t − kδ) ,
{k} =
q k −1
q−1
is a q-number ,
{k}! = {1}{2} . . . {k} is a q-factorial .
tδ D+δ = tD−δ
,
tq D q = t
d
dt
sl (2)-algebra realized by finite-difference operators
(on uniform lattice of spacing δ)
2
J+ = −t (2) δD−δ
+ t[t − δ(n + 1)]D−δ − nt
J0 = tD−δ
J− = D+δ
with Pn = h 1, t, t 2 , . . . t n i as common invariant subspace
sl (2)-algebra realized by finite-difference operators
(on exponential lattice of dilation q)
d
− ntq
dt
d
J0 = t
dt
J− = Dq
J + = tq t
with Pn = h 1, t, t 2 , . . . t n i as common invariant subspace
Take Laguerre operator
1
ht = −t∂t2 + (t − p − )∂t
2
Eigenstates:
where
(p− 1 )
Ln 2 (t)
(p− 12 )
φn = Ln
(t)
and
ǫn = n,
is associated Laguerre polynomial.
n ∈ N,
1
ht,δ (t, D±δ ) = −[t + (p + )]D+δ + 2tD−δ
2
The operator ht,δ (t, D±δ ) is a non-local, three-point,
finite-difference operator on uniform lattice in t-space
s
φ(t − δ)
s
φ(t)
s
φ(t + δ)
The corresponding spectral problem at δ = 1
1 1 − t + (p + ) φ(t + 1) + 3t + (p + ) φ(t) − 2tφ(t − 1)
2
2
= ǫφ(t)
eigenfunctions are δ-modified associated Laguerre polynomials
(p− 1 )
L̂n 2 (t; δ)
=
n
X
(ν− 21 ) (ℓ)
aℓ
ℓ=0
The operators hht,δ and ht are isospectral.
t
1
ht,d (t, ∂t , Dq ) = −t∂t Dq + t∂t − (p + )Dq
2
The operator ht,d (t, ∂t , Dq ) is a non-local, two-point,
differential-difference operator on exponential lattice in t-space.
Its eigenfunctions can be called q-modified associated Laguerre
polynomials
n
X
(p− 1 )
(p− 1 ) ℓ! ℓ
L̂n 2 (t, q) =
aℓ 2
t ,
{ℓ}!
ℓ=0
The operators ht,d , hht,δ and ht are isospectral.
Immediate application of Lie-algebra formalism algebraic perturbation theory.
Take One-dimensional Anharmonic Oscillator
H =
1 ∂2
g
−
+ ω2 x 2 + 2
+ 2λω 3 x 4
2
2
∂x
x
|
{z
}
A1 −rational (2-body Calogero) model
ω
ψ0 = x ν e − 2
h =
x2
, g = ν(ν − 1) , t = ωx 2
1 −1
ω
ψ0 (H − (1 + 2ν))ψ0 = −t∂t2 + (t − ν − 1/2)∂t + λt 2
2ω
2
t 2 ∈ P2
(h0 + λh1 )φ = ǫφ
Perturbation theory:
⋆ Ground State:
φ=
P
φ0 = 1,
λn φn , ǫ =
ǫ0 = 0
P
λn ǫn
First correction:
−t∂t2 φ1 + (t − ν − 1/2)∂t φ1 = ǫ1 − t 2
1 2
3
1
3
t + (ν + )t , E1 = (ν + )(ν + )
2
2
2
2
Second correction:
−φ1 =
−t∂t2 φ2 + (t − ν − 1/2)∂t φ2 = ǫ2 + (ǫ1 − t 2 )φ1
4 t
11 ν
31 + 24ν + 4ν 2 2 (3 + 2ν)(7 + 4ν)
3
+
+
t +
t +
t
φ2 =
8
12 2
8
2
(1 + 2ν)(3 + 2ν)(7 + 4ν)
2
In general, φn = P2n (t) and coeffs in front of leading terms can be
found explicitly !
(generalized Catalan numbers)
E2 = −
Do exist quantum systems
with hidden algebra gl (d + 1) ?
gld+1 -algebra (in R d )
(almost degenerate or totally symmetric, Young tableaux is a row)
(n, 0, 0, . . . 0)
| {z }
d−1
∂
,
∂ti
∂
= ti
,
∂tj
Ji− =
Jij 0
◮
i , j = 1, 2 . . . d ,
∂
−n,
∂ti
i =1


d
X
∂
= ti J 0 = ti 
tj
− n ,
∂tj
J0 =
Ji+
d
X
i = 1, 2 . . . d ,
ti
(d + 1)2 generators
j=1
i = 1, 2 . . . d .
◮
if n = 0, 1, 2 . . ., fin-dim irreps
(d)
Pn
= ht1 p1 t2 p2 . . . td pd | 0 ≤ Σpi ≤ ni
Remark. The flag P (d) is made out of finite-dimensional
(d)
irreducible representation spaces Pn of the algebra gld+1 taken in
realization (∗).
Any operator made out of generators (∗) has
finite-dimensional invariant subspace which is
finite-dimensional irreducible representation space and visa
versa.
To the best of my knowledge almost all known explicitly
(algebraically) eigenfunctions have a form
Ψ(x) = (polynomial in φ(x)) × factor
with a non-singular function in the domain x as factor.
What is a meaning (if any) of variables φ(x)?
Hamiltonian Reduction Method
(Olshanetsky-Perelomov ’77, Kazhdan-Kostant-Sternberg ’78)
◮
Define Laplace-Beltrami operators on symmetric spaces of
simple Lie groups (free/harmonic oscillator motion)
◮
Radial parts of L-B operators ≡ Olshanetsky-Perelomov
Hamiltonians relevant from physical point of view. They can
be associated with root systems.
Rational case:
N 1X
∂2
1 X
| α| 2
2 2
H=
− 2 + ω xk +
ν|α| (ν|α| − 1)
2
2
(α · x)2
∂xk
k=1
α∈R+
where R+ is a set of positive roots and ν|α| are coupling constants
depending on the root length.
For all roots of the same length ν|α| = ν.
⋆ They take discrete values but can be generalized to any value.
Configuration space - Weyl chamber.
Ground state wave function
Ψ0 (y ) =
Y
α∈R+
|(α · y )|ν|α| e −ωy
2 /2
The Hamiltonian is completely-integrable
(super-integrable) and exactly-solvable for any value of
ν > − 12 and ω > 0. It is invariant wrt Weyl (Coxeter)
group transformation (symmetry group of root space)
Trigonometric case:
N 1X
∂2
β2 X
| α| 2
H =
− 2 +
ν|α| (ν|α| − 1) 2 β
2
8
∂yk
sin 2 (α · y )
k=1
α∈R+
where R+ is a set of positive roots and ν|α| are coupling constants
depending on the root length.
⋆ They take discrete values but can be generalized to any value.
Configuration space - Weyl alcove.
Ground state wave function
ν|α|
Y β
Ψ0 (y ) =
sin
(α
·
y
)
2
α∈R+
The Hamiltonian is completely-integrable and
exactly-solvable for any value of ν > − 12 . It is invariant
wrt Weyl group transformation + periodic.
Procedure:
◮
Gauging away ground state eigenfunction (similarity
transformation) (Ψ0 )−1 (H − E0 )Ψ0 = h
◮
Olshanetsky-Perelomov Hamiltonians (OPH) possess different
symmetries (permutations, translation-invariance, reflections,
periodicity etc). These symmetries correspond to the Weyl
(Coxeter) group plus translations. By coding these symmetries
to new coordinates (taking the Weyl (Coxeter) invariants as
new coordinates) we find ’premature’ (undressed by
symmetries) operators to these Hamiltonians.
Example: Weyl(An ) = S n + T
WHAT ARE THESE COORDINATES?
◮
Rational case – Weyl (Coxeter)-invariant variables:
X
(Ω)
ta (x) =
(α, x)a ,
α∈Ω
◮
where a’s are the degrees of the Weyl (Coxeter) group W and
Ω is an orbit.
The invariants t are defined ambiguously, they depend on
chosen orbit, but always lead to rational OPH h in a form of
algebraic operator with polynomial coeffs.
Trigonometric case – trigonometric Weyl-invariant variables:
X
(Ω)
τa (y ) =
e i β(α,y ) ,
α∈Ωa
where Ωa is an orbit generated by fundamental weight
αa , a = 1, 2, . . . , r (r – rank of the root system)
The invariants τ taken as coordinates always lead to
trigonometric OPH h in a form of algebraic operator with
polynomial coeffs.
◮
Calogero Model (AN−1 Rational model)
(F. Calogero, ’69)
N identical particles on a line with singular pairwise interaction
x1 < x2 < x3 < .
HCal
. . .
< xN
N N
X
∂2
1X
1
2 2
− 2 + ω xi
+g
=
2
∂xi
(xi − xj )2
i =1
i >j
Ψ0 (x) =
Y
i <j
ω
|xi − xj |ν e − 2
P
xi2
, g = ν(ν − 1)
hCal = 2Ψ−1
0 (HCal − E0 ) Ψ0
X
1
Y =
xi , yi = xi − Y , i = 1, . . . , N
N
(x1 , x2 , . . . xN ) → Y , tn (x) = σn (y (x))| n = 2, 3 . . . N
X
σk (x) =
xi 1 xi 2 . . . xi k
i1 <i2 <...<ik
∂2
∂
+ Bi (t)
∂ti ∂tj
∂ti
X
(N − i + 1)(1 − j)
Aij =
ti −1 tj−1 +
(2l − j + i )ti +l−1 tj−l−1
N
hCal = Aij (t)
l≥max(1,j−i )
Bi =
1
(1 + νN)(N − i + 2)(N − i + 1) ti −2 + 2ω (i − 1) ti
N
Eigenvalues:
ǫn = 2ω
N
X
i =2
(i − 1) ni
the spectra of anisotropic harmonic oscillator, linear in quantum
numbers.
Hamiltonian:
h = Pol (Ji− , Jij 0 )
gl (N − 1) is the hidden algebra of N-body Calogero model.
Eigenfunctions:
they are elements of the flag P (N−1) .
◮
Sutherland Model (AN−1 Trigonometric model)
(B Sutherland, ’69)
N identical particles on a circle with singular pairwise
interaction
x2
x3
x1
.
.
.
.
xN
HSuth = −
N
1 X ∂2
gX
1
+
2
1
2
2
4
∂xk
sin ( 2 (xk − xl ))
k=1
k<l
Ψ0 (x) =
Y
sin
i <j
ν
1
(xi − xj ) , g = ν(ν − 1)
2
hSuth = −2Ψ−1
0 (HSuth − E0 ) Ψ0
X
1
Y =
xi , yi = xi − Y , i = 1, . . . , N
N
(x1 , x2 , . . . xN ) → e iY , ηn (x) = σn (e iy (x) )| n = 1, 2 . . . (N − 1)
∂2
∂
+ Bi (η)
∂ηi ∂ηj
∂ηi
X
(N − i ) j
=
ηi ηj +
(j − i − 2l ) ηi +l ηj−l
N
hSuth = Aij (η)
Aij
l≥max(1,j−i )
Bi = (
1
+ ν) i (N − i ) ηi
N
Eigenvalues:
ǫn = Pol2 (ni )
quadratic in quantum numbers.
Hamiltonian:
h = Pol (Ji− , Jij 0 )
gl (N − 1) is the hidden algebra of N-body Sutherland model.
Eigenfunctions:
they are elements of the flag P (N−1) .
◮
BCN –Rational model
N
1X
HBCN = −
2
i =1
+
g2
2
∂2
− ω 2 xi2
∂xi 2
N
X
i =1

Ψ0 = 
Y
i <j
+g
X
i <j
1
1
+
(xi − xj )2 (xi + xj )2
1
xi2
|xi − xj |ν |xi + xj |ν
N
Y
i =1

ω
|xi |ν2  e − 2
PN
g = ν(ν − 1), g2 = ν2 (ν2 − 1) ,
hBC N = (Ψ0 )−1 (HBCN − E0 ) Ψ0
(x1 , x2 , . . . xN ) → σk (x 2 )| k=1,2,...,N
X
σk (x) =
xi 1 xi 2 · · · xi k
i1 <i2 <···<ik
2
i =1 xi
,
hBCN = Aij (σ)
Aij
Bi
= −2
=
∂2
∂
+ Bi (σ)
∂σi ∂σj
∂σi
X
(2l + 1 + j − i ) σi −l−1 σj+l
l≥0
[1 + ν2 + 2ν(N − i )] (N − i + 1) σi −1 + 2 ω i σi
Eigenvalues:
ǫn = 2ω
N
X
i ni
i =1
the spectra of anisotropic harmonic oscillator, linear in quantum
numbers.
Hamiltonian:
h = Pol (Ji− , Jij 0 )
gl (N) is the hidden algebra of BCN -rational model.
Eigenfunctions:
they are elements of the flag P (N) .
◮
BCN –Trigonometric model (Inozemtsev model)
"
N
N
1 X ∂2
gX
+
HBCN =−
2
∂xi 2 4
sin2
i =1
i <j
+
1
+ 2
1
sin
2 (xi − xj )
N
N
g2 X 1
g3 X 1
+
.
4
4
sin2 xi
sin2 x2i
i =1
i =1
1
1
2 (xi + xj )
N
Y
1
1
Ψ0 = | sin( (xi − xj ))|ν | sin( (xi + xj ))|ν
2
2
i <j
N
Y
i =1
xi
| sin(xi )|ν2 | sin( )|ν3 ,
2
g = ν(ν − 1), g2 = ν2 (ν2 − 1) , g3 = ν3 (ν3 + 2ν2 − 1) ,
hBC N = −2(Ψ0 )−1 (HBCN − E0 ) Ψ0
(x1 , x2 , . . . xN ) → σ̂k (x) = σk (cos(x))| k = 1, 2 . . . N
#
hBCN = Aij (σ̂)
∂2
∂
+ Bi (σ̂)
∂ σ̂i ∂ σ̂j
∂ σ̂i
Xh
Aij =N σ̂i −1 σ̂j−1 −
(i − l ) σ̂i −l σ̂j+l + (l + j − 1) σ̂i −l−1 σ̂j+l−1
l≥0
−(i − 2 − l ) σ̂i −2−l σ̂j+l − (l + j + 1) σ̂i −l−1 σ̂j+l+1
Bi =
i
i
h
ν3
ν3
(i − N − 1) σ̂i −1 − ν2 +
+ 1 + ν(2N − i − 1) i σ̂i
2
2
−ν(N − i + 1)(N − i + 2)σ̂i −2
Eigenvalues:
ǫn = Pol2 (ni )
quadratic in quantum numbers.
Hamiltonian:
h = Pol (Ji− , Jij 0 )
gl (N) is the hidden algebra of BCN trigonometric model.
Eigenfunctions:
they are elements of the flag P (N)
◮
Both AN − and BCN − rational and trigonometric models
possess algebraic forms associated with preservation of the
same flag of polynomials P (N) . The flag is invariant wrt
linear transformations in space of orbits t 7→ t + A .
◮
Their Hamiltonians (as well as higher integrals) can be written
in the algebraic form
(∗)
h = P2 (J (b ⊂ glN+1 ))
where P2 is a polynomial of second degree in the generators
J of the maximal affine subalgebra of the algebra glN+1 in
realization (∗). Hence glN+1 is their hidden algebra. From
this viewpoint all four models are different faces of a single
model.
◮
Supersymmetric AN − and BCN − rational and trigonometric
models possess algebraic forms, preserve the same flag of
(super)polynomials and their hidden algebra is the
superalgebra gl (N + 1|N).
Do exist other quantum systems with gl (n) hidden algebra, with
different Young tableau, different realization?
(i) BCN -Elliptic model
(ii) Matrix systems
(iii) Discrete systems on uniform, exponential, mixed
uniform-exponential lattices
◮
For the OPH Hamiltonians for all exceptional root spaces
G2 , F4 , E6,7,8 (for both rational and trigonometric) and
non-crystallographic H3,4 , I2 (k) the eigenfunctions are
polynomials in their invariants (in symmetric variables).
◮
Their hidden algebras are new infinite-dimensional but
finite-generated algebras of differential operators. All of them
have finite-dimensional invariant subspaces in polynomials.
◮
Generating elements of any such hidden algebra can be
grouped in even number of (conjugated) Abelian algebras Li ,
Li and one Lie algebra B.
B
⋉
⋉
L
6
-
L
Pp (B)
Figure: Triangular diagram relating the subalgebras L, L and B. p is
integer. It is a generalization of Gauss decomposition for semi-simple
algebras (p = 1).
G2 -case: three-body problem with 2- and 3-body interaction
p=2
J 1 = ∂x , J 2 = x∂x −
B [gl (2)] :
n
n
, J 3 = 2y ∂y − ,
3
3
J 4 = xJ0 ≡ x(x∂x + 2y ∂y − n) ,
R0 = ∂y , R1 = x∂y , R2 = x 2 ∂y
L:
L:
2
T2 = y ∂xx
, T1 = yJ0 ∂x , T0 = yJ0 (J0 + 1)
(2)
Pn
= hx p1 y p2 | 0 ≤ p1 + 2p2 ≤ ni
To the best of my knowledge almost all known explicitly
(algebraically) eigenfunctions have a form
Ψ(x) = (polynomial in φ(x)) × factor
with a non-singular function in the domain x as factor.
What is a meaning (if any) of variables φ(x)?
Invariants of the discrete group of symmetry of the system.