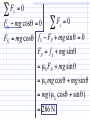Download f F = mg X

y
Apply Newton’s 2nd Law
FN
FA
f
x
mg
❑ If
X
Fy = FN
X
mg = may = 0
FN = mg
Fx = FA
f = max
applied force is small, book does not move
(static), ax=0, then f=fs
FA = f S
❑ Increase applied force, book still does not move
❑ Increase FA more, now book moves, ax≠0
FA − f S = ma x ⇒ FA = f S + ma x > f S
❑ There is some maximum static frictional force,
fsmax. Once the applied force exceeds it, the book
moves
Magnitudes not
~max
~
| fs
| = µ s | FN |
vectors
• µs is the coefficient of static friction, it is a
dimensionless number, different for each
surface-object pair (wood-wood, wood-metal);
also depends on surface preparation
• µs does not depend on the mass or surface
area of the object
• Has value: 0 < µs < 1.5
• If no applied vertical force
f
max
S
= µ S mg
❑ Push down on
book
y
FN
FA
❑ Apply Newton’s 2nd
Law
∑F
y
FP
f
x
mg
= FN − mg − FP = ma y = 0
FN = mg + FP
f
max
S
= µ S FN = µ S (mg + FP )
❑ What is FA needed just to start book moving?
∑F
x
= FA − f S = 0 ⇒ FA = f
max
S
= µ S (mg + FP )
When an Object is Moving?
❑ fsmax is exceeded so the object can move, but
friction force is still being applied.
❑ However, less force is needed to keep an object
moving (against friction) than to get it started
❑ We define kinetic friction
f k = µ k FN
❑ µk is the coefficient of kinetic friction, similar to
µS but always less than µS
• Now, let’s consider incline plane problem, but with
friction (but first do a simpler example)
Example Problem
When you push a 1.80-kg book on a tabletop, it
takes 2.25 N to start the book sliding. Once it is
sliding, however, it takes 1.50 N to keep the book
moving with constant speed. What are the
coefficients of static and kinetic friction between
the book and the table top?
❑ Book is at rest
❑ m = 1.00 kg, θ = 10.0°, µs = 0.200 y
y
fs
FBD
fs
FN
mg
θ
FN
θ
x
θ
x
mg
∑F
y
= FN − mg cosθ = 0
∑F
x
FN = mg cosθ
= mg sin θ − f S = 0
f S = mg sin θ
o
o
= (1.0kg )(9.80 )(cos10.0 ) = (1.00kg)(9.80 )(sin 10.0 )
m
s2
= 9.65 N
m
s2
= 1.70 N
❑ Book can move (slide) if mgsinθ ≥ fsmax
❑ What is fsmax?
f
max
S
= µ S FN = (0.200)(9.65 N)
= 1.93 N > f S
Book does not move.
❑ What angle is needed to cause book to slide?
max
S
mg sin θ ≥ f
mg sin θ ≥ µ S FN
mg sin θ ≥ µ S mg cos θ
tan θ ≥ µ S
−1
θ ≥ tan ( µ S )
o
≥ 11.3
❑ As θ is increased, FN
decreases, therefore
fsmax decreases
❑ Once book is moving, we need to use the
kinetic coefficient of friction
❑ Lets take, θ = 15.0° and µk = 0.150 < µs
∑F
x
= mg sin θ − f k = ma x
= mg sin θ − µ k mg cosθ = ma x
or a x = g (sin θ − µ k cosθ )
o
o
= (9.80 )(sin 15.0 − 0.150 cos15.0 )
m
s2
= 1.12 sm2
Example Problem
A skier is pulled up a slope at a constant velocity
by a tow bar. The slope is inclined at 25.0° with
respect to the horizontal. The force applied to the
skier by the tow bar is parallel to the slope. The
skier’s mass is 55.0 kg , and the coefficient of
kinetic friction between the skis and the snow is
0.120. Find the magnitude of the force that the
tow bar exerts on the skier.
❑ Given: m = 55.0 kg, µk = 0.120, θ = 25.0°
❑ Infer: since velocity is constant, ax=0; also
ay=0 since skier remains on slope
⇒
!
equilibrium
∑F = 0⇒ ∑F
x
= 0, ∑ Fy = 0
Draw FBD, apply Newton’s 2nd Law
Fp
Fp
FN
FN
fk
mg
θ
fk
x
θ
θ
mg
x
∑F
y
=0
FN − mg cosθ = 0 ∑ Fx = 0
FN = mg cosθ f k − FP + mg sin θ = 0
FP = f k + mg sin θ
= µ k FN + mg sin θ
= µ k mg cosθ + mg sin θ
= mg ( µ k cosθ + sin θ )
= 286 N
The Tension Force
rope
FN
FBD of crate
T
T
Crate, m
mg
frictionless
Frictionless
pulley
❑ Assume rope is massless
and taut
FBD of rope
T
T
-T
∑F
x
T
= T −T = 0
m
Crate at rest
∑F
mg
= T − mg = 0
T = mg
y
❑ Like the normal force, the friction and tension
forces are all manifestations of the electromagnetic
force
❑ They all are the result of attractive (and
repulsive) forces of atoms and molecules within an
object (normal and tension) or at the interface of
two objects
Applications of Newton’s 2nd Law
❑ Equilibrium – an object which has zero
acceleration, can be at rest or moving with
constant velocity
!
∑F = 0⇒ ∑F
x
= 0, ∑ Fy = 0
❑ Example: book at rest on an incline with friction
❑ Non-equilibrium – the acceleration of the
object(s)
is
non-zero
!
!
∑ F = ma ⇒ ∑ Fx = max , ∑ Fy = ma y
Example Problem
Three objects are connected by strings that pass over
massless and frictionless pulleys. The objects move
and the coefficient of kinetic friction between the
middle object and the surface of the table is 0.100
(the other two being suspended by strings). (a) What
is the acceleration of the three objects? (b) What is
the tension in each of the two strings?
❑ Given: m1 = 10.0 kg,
m2=80.0 kg, m3=25.0
m1
kg, µk=0.100
m2
m3
❑ Find: a1, a2, a3, T1,
and T2
Solution: 1) Draw free-body diagrams
T1
T2
m3
m1
FN
y
T1
T2
fk
m1g
m3g
m2g
2) Apply Newton’s 2nd Law to each object
x
∑F
y1
∑F
= m1a y1
y3
= m3 a y 3
T1 − m1 g = m1a y1
T2 − m3 g = m3 a y 3
T1 = m1 (a y1 + g )
T2 = m3 (a y 3 + g )
∑ Fx 2 = m2 ax 2
T2 − T1 − f k = m2 a x 2
Also, ax1=0, ax3=0, ay2=0
X
FN
Fy2 = 0
m2 g = 0
FN = m2 g
f k = µ k FN = µ k m2 g
T2 − T1 − µ k m2 g = m2 a x 2
T1 = m1 (a y1 + g )
T2 = m3 (a y 3 + g )
❑ Three equations, but
five unknowns:
ay1,ay3,ax2,T1,and T2
❑ But, ay1 = ax2 = -ay3 = a
❑ Substitute 2nd and 3rd equations into the 1st
equation
m3 (−a + g ) − m1 (a + g ) − µ k m2 g = m2 a
− m3 a + m3 g − m1a
− m1 g − µ k m2 g − m2 a = 0
a (−m3 − m1 − m2 )
+ g (m3 − m1 − µ k m2 ) = 0
a (m1 + m2 + m3 ) = g (m3 − m1 − µ k m2 )
(m3 − m1 − µ k m2 )
a=g
(m1 + m2 + m3 )
' 25.0 − 10.0 − 80.0(0.100) $
= 9.80 %
"
& 10.0 + 80.0 + 25.0
#
m
= 0.60 s 2 = a y1 = a x 2 = −a y 3
T1 = m1 (a + g ) = 10.0(0.60 + 9.80)
= 104 N
T2 = m3 ( g − a ) = 25.0(9.80 − 0.60)
= 230 N
Example (simple)
Pulling up on a rope, you lift a 4.35-kg
bucket of water from a well with an
acceleration of 1.78 m/s2. What is the tension
in the rope?
❑