Download I (x) - Boston University Physics Department.

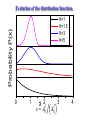
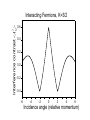
Interference between fluctuating condensates
Anatoli Polkovnikov,
Boston University
Collaboration:
Ehud Altman
Eugene Demler Vladimir Gritsev -
Weizmann
Harvard
Harvard
What do we observe interfering ideal condensates?
TOF
Measure (interference part):
md
I ( x)  AQ e  A e , AQ  a a , Q 
t
i1,2
a1,2
Ne
 I ( x) N cos  Qx   
iQx
d
x
†  iQx
Q
†
1 2
Andrews et. al. 1997
a) Correlated phases ( = 0)
  I (x)  N cos(Qx)
b) Uncorrelated, but well defined phases   I(x)   0
I ( x) I ( y )
N 2 cos  Qx    cos  Qy   
~ N 2 cos  Q( x  y )   0
Hanbury BrownTwiss Effect
c) Initial number state. No phases?
Work with original bosonic fields:
I ( x) I ( y )
a1† a1 a2† a2 cos  Q ( x  y ) 
 AQ2 cos(Q( x  y ))  N 2 cos  Q ( x  y ) 
The same answer as in the case b) with random but well
defined phases!
Easy to check
that at large N:
2 2
Q
 A  A
4
Q
2
Q
A
0
The interference amplitude does not fluctuate!
First theoretical explanation: I. Casten and J. Dalibard (1997): showed that
the measurement induces random phases in a thought experiment.
Experimental observation of interference between ~ 30 condensates
in a strong 1D optical lattice: Hadzibabic et.al. (2004).
Z. Hadzibabic et. al., Phys. Rev. Lett. 93, 180401 (2004).
Polar plots of the fringe amplitudes and phases for 200
images obtained for the interference of about 30
condensates. (a) Phase-uncorrelated condensates. (b)
Phase correlated condensates. Insets: Axial density
profiles averaged over the 200 images.
Imaging beam
What if the condensates are fluctuating?

L
This talk:
1. Access to correlation functions.
a) Scaling of  AQ2  with L and : power-law exponents. Luttinger
liquid physics in 1D, Kosterlitz-Thouless phase transition in 2D.
b) Probability distribution W(AQ2): all order correlation functions.
c) Fermions: cusp singularities in  AQ2 ( ) corresponding to kf.
2. Direct simulator (solver) for interacting problems.
Quantum impurity in a 1D system of interacting fermions (an example).
3. Potential applications to many other systems.
What are the advantages compared to the
conventional TOF imaging?
1. TOF relies on free atom expansion. Often not true in strongly
correlated regimes. Interference method does not have this
problem.
2. It is often preferable to have a direct access to the spatial
correlations. TOF images give access either to the momentum
distribution or the momentum correlation functions.
3. Free expansion in low dimensional systems occurs
predominantly in the transverse directions. This renders bad
signal to noise. In the interference method this is advantage:
longitudinal correlations remain intact.
One dimensional systems.
1. Algebraic correlations at zero temperature (Luttinger
liquids). Exponential decay of correlations at finite
temperature.
2. Fermionization of bosons, bosonization of fermions. (There
is not much distinction between fermions and bosons in
1D).
3. 1D systems are well understood. So they can be a good
laboratory for testing various ideas.
Scaling with L: two limiting cases
I   z N cos  Qx  z 
Dephased condensates:
z
AQ  L
Interference contrast
does not depend on L.
L
x
L
x
Ideal condensates:
z
AQ  L
Contrast scales
as L-1/2.
The phase distribution of an elongated 2D Bose gas.
(courtesy of Zoran Hadzibabic)
Matter wave
interferometry
0
p
very low temperature:
straight fringes which
reveal a uniform phase
in each plane
“atom lasers”
higher temperature:
bended fringes
from time to time:
dislocation which
reveals the presence
of a free vortex
S. Stock, Z. Hadzibabic, B. Battelier, M. Cheneau,
and J. Dalibard: Phys. Rev. Lett. 95, 190403 (2005)
Formal derivation.
L
AQ
2
Q
A
L
L
0
0

A
L
L
0

 
0
L
0
a1† ( z )a2 ( z )dz 
L
0
a1† ( z1 )a2 ( z1 )a2† ( z2 )a1 ( z2 )dz1dz2
Independent condensates:
z
2
Q
L
a1† ( z1 )a1 ( z2 ) a2 ( z1 )a2† ( z2 ) dz1dz2
2
a1† ( z )a1 (0) dz for identical homogeneous systems
Long range order:
a1† ( z )a1 (0)
const 
AQ2  L2
short range correlations:
a1† ( z )a1 (0)
e z / 
AQ2  L

Intermediate case (quasi long-range order).
L
L
AQ2
L
0
2
a1† ( z )a1 (0) dz
1D condensates (Luttinger liquids):
a ( z)a1 (0)   h / z 
z
2
Q
A
21/ K
L

1/ K
h
1/ 2 K
†
1
, Interference contrast  h / L 
1/ 2 K
Repulsive bosons with short range interactions:
Weak interactions K
1 
AQ2
L2
1
Strong interactions (Fermionized regime) K
Finite temperature:
A
11/ K

1
L h  

 m h T 
2
2
Q
AQ2
2
L
x(z1)
x(z2)
Angular Dependence.
(for the imaging beam
orthogonal to the
page,  is the angle of
the integration axis
with respect to z.)
z



I
0
AQ
2
Q
A
L
L
L
0
0

a1† ( z )a2 ( z )eiQ ( x  z tan  ) dz ,

L
0

a1† ( z )a2 ( z )e iqz dz , q  Q tan 
a1† ( z1 )a1 ( z2 ) a2 ( z1 )a2† ( z2 )  eiq ( z2  z1 ) dz1dz2
q is equivalent to the relative momentum of the two condensates
(always present e.g. if there are dipolar oscillations).
Angular (momentum) Dependence.
L
2
Q
A
qL
L
0
†
a ( z )a(0)
A
2
Q
A
AQ2
cos(qz ) dz
1
AQ2    q  ,
2
Q
2
ideal condensates ( K
1);
1

, finite T (short range correlations);
2 2
1 q 

1
11/ K
q
,
quasi-condensates finite K.
has a cusp singularity for K<1, relevant for fermions.
Higher moments (need exactly two condensates).
2n
Q
A

L
0

L
†
†
a ( z1 )
0

a ( zn )a( z1 )

a( z n )
2
dz1

dzn
Relative width of the distribution (no dependence on L at large L):

2 2
Q
A  A
4
Q
K 1
 1,
 ~
p 6 K , K 1
2
Q
A
Wide Poissonian distribution in the
fermionized regime (and at finite
temperatures).
Narrow distribution in the weakly
interacting regime. Absence of
amplitude fluctuations for true
condensates.
Evolution of the distribution function.
Probability P(x)
K=1
K=1.5
K=3
K=5
0
1
2
x
x  A2
Q
AQ2
3
4
Connection to the impurity in a Luttinger liquid problem.
Boundary Sine-Gordon theory:
Z   D exp  S ,
S
pK
2
Z 
n




x2n
dx  d
0
P. Fendley, F. Lesage, H.~Saleur (1995).
           2g 
2
2

x
Z 2 n , x  g   2p  
1/ 2 K
 n!
2

0
d cos 2p (0, )
,
Z 2n 
2n
Same integrals as in the expressions for AQ

Z ( x)   P( A ) I 0 (2 Ax / A0 )dA ,
0
2
2
11/ 2 K
A0  L
Sounds complicated? Not really.
1. Do a series of experiments and determine the distribution function.
Distribution of interference amplitudes (and phases) from two 1D condensates.
T. Schumm, et.
al., Nature Phys.
1, 57 (2005).
2. Evaluate the integral. Z ( x) 


0
2
2
P( A ) I 0 (2 Ax / A0 )dA ,
3. Read the result. Direct experimental simulation of a quantum
impurity problem.
Spinless Fermions.
2
Q
A
L
L
0
†
a ( z )a (0)
2
a ( z )a (0) 
†
dz ,
sin(k f z )
z

1 2 K  K 1

2
Note that K+K-1  2, so AQ  L and the distribution function
is always Poissonian.
However for K+K-1  3 there is a universal cusp at nonzero
momentum as well as at 2kf:
2
Q
A ( q)
L
L
0
†
a ( z)a(0)
A (q)  A (0)  q
2
Q
2
Q
2
cos  qz  dz,
K  K 1 1
q  Q tan 
. There is a similar cusp at 2kf
0.6
2
Interference contrast AQ
Interacting Fermions, K=3/2
0.4
0.2
0.0
-0.2
-0.4
-6
-4
-2
0
2
4
6
Incidence angle (relative momentum)
Two dimensional condensates at finite temperature.
Similar setup to 1D.
S. Stock et.al : Phys. Rev. Lett.
95, 190403 (2005)
Ly
Lx
Can also study size or
angular (momentum)
dependence.
Lx
2
Q
A
Ly
Lx Ly  dx  dy a ( x, y )a (0, 0)
†
0
0
2
Observing the Kosterlitz-Thouless transition
Ly
Above KT transition
Lx
2
Q
A
  Lx Ly
2
Below KT transition
2
Q
A
  Lx Ly 
2 
Universal jump in  at TKT
T  TKT
    1
T

TKT
   1/ 4
Expect a similar jump in the
distribution function.
Conclusions.
1. Analysis of interference between independent condensates reveals
a wealth of information about their internal structure.
a) Scaling of interference amplitudes with the system size or the
probing beam angle gives the correlation functions exponents.
b) Probability distribution ( = full counting statistics in TOF) of
amplitudes for two condensates contains information about higher
order correlation functions.
c) Interference of two Luttinger liquids directly realizes the statistical
partition function of a one-dimensional quantum impurity problem.
2. Vast potential applications to many other systems, e.g.:
a) Spin-charge separation in spin ½ 1D fermionic systems.
b) Rotating condensates (instantaneous measurement of the
correlation functions in the rotating frame).
c) Correlation functions near continuous phase transitions.
d) Systems away from equilibrium.