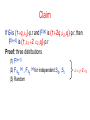Download ppt

Cryptography and Privacy Preserving
Operations
Lecture 1
Lecturer: Moni Naor
Weizmann Institute of Science
What is Cryptography?
Traditionally: how to maintain secrecy in communication
Alice and Bob talk while Eve tries to listen
Bob
Alice
Eve
History of Cryptography
• Very ancient occupation
• Many interesting books and sources, especially
about the Enigma
– David Kahn, The Codebreakers, 1967
– Gaj and Orlowski, Facts and Myths of Enigma:
Breaking Stereotypes, Eurocrypt 2003
• Not the subject of this course
Modern Times
• Up to the mid 70’s - mostly classified military work
– Exception: Shannon, Turing*
• Since then - explosive growth
– Commercial applications
– Scientific work: tight relationship with Computational
Complexity Theory
– Major works: Diffie-Hellman, Rivest, Shamir and Adleman
(RSA)
• Recently - more involved models for more diverse tasks.
How to maintain the secrecy, integrity and functionality
in computer and communication system.
Cryptography and Complexity
Complexity Theory • Study the resources
needed to solve
computational problems
– computer time, memory
• Identify problems that are
infeasible to compute.
Cryptography • Find ways to specify
security requirements of
systems
• Use the computational
infeasibility of problems in
order to obtain security.
The development of these two areas is tightly connected!
The interplay between these areas is the subject of the course
Key Idea of Cryptography
Use the intractability of some problems for
the advantage of constructing secure
system
Short Course Outline
First part of this short course:
– Alice and Bob want to cooperate
– Eve wants to interfere
• One-way functions,
• pseudo-random generators
• pseudo-random functions
• Encryption
Second part
– Alice and bob do not quite trust each other
• Zero-knowledge protocols
• Secure function evaluation
Three Basic Issues in Cryptography
• Identification
• Authentication
• Encryption
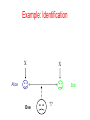
Example: Identification
• When the time is right, Alice wants to send an
`approve’ message to Bob.
• They want to prevent Eve from interfering
– Bob should be sure that Alice indeed approves
Alice
Bob
Eve
Rigorous Specification of Security
To define security of a system must specify:
1. What constitute a failure of the system
2. The power of the adversary
– computational
– access to the system
– what it means to break the system.
Specification of the Problem
Alice and Bob communicate through a channel
Bob has two external states {N,Y}
Eve completely controls the channel
Requirements:
• If Alice wants to approve and Eve does not interfere –
Bob moves to state Y
• If Alice does not approve, then for any behavior from
Eve, Bob stays in N
• If Alice wants to approve and Eve does interfere - no
requirements from the external state
Can we guarantee the requirements?
• No – when Alice wants to approve she sends (and
receives) a finite set of bits on the channel. Eve can
guess them.
• To the rescue - probability.
– Want that Eve will succeed with low probability.
– How low? Related to the string length that Alice sends…
Example: Identification
X
X
Alice
Bob
Eve
??
Suppose there is a setup period
• There is a setup where Alice and Bob can agree on a
common secret
– Eve only controls the channel, does not see the internal state
of Alice and Bob (only external state of Bob)
Simple solution:
– Alice and Bob choose a random string X R {0,1}n
– When Alice wants to approve – she sends X
– If Bob gets any symbols on channel – compares to X
• If equal moves to Y
• If not equal moves permanently to N
Eve’s probability of success
• If Alice did not send X and Eve put some string X’
on the channel, then
– Bob moves to Y only if X= X’
Prob[X=X’] ≤ 2-n
Good news: can make it a small as we wish
• What to do if Alice and Bob cannot agree on a
uniformly generated string X?
Less than perfect random variables
• Suppose X is chosen according to some
distribution Px over some set of symbols Γ
• What is Eve’s best strategy?
• What is her probability of success
(Shannon) Entropy
Let X be random variable over alphabet Γ with distribution Px
The (Shannon) entropy of X is
H(X) = - ∑ x Γ Px (x) log Px (x)
Where we take 0 log 0 to be 0.
Represents how much we can compress X
Examples
• If X=0 (constant) then H(x) = 0
– Only case where H(x) = 0 is when x is constant
– All other cases H(x) >0
• If X  {0,1} and Prob[X=0] = p and
Prob[X=1]=1-p, then
H(X) = -p log p + (1-p) log (1-p) ≡ H(p)
If X  {0,1}n and is uniformly distributed, then
H(X) = - ∑
n
x  {0,1}n 1/2
log 1/2n = 2n/2n n = n
Properties of Entropy
• Entropy is bounded H(X) ≤ log | Γ | with equality
only if X is uniform over Γ
Does High Entropy Suffice for
Identification?
• If Alice and bob agree on X  {0,1}n where X has high
entropy (say H(X) ≥ n/2 ), what are Eve’s chances of
cheating?
• Can be high: say
– Prob[X=0n ] = 1/2
– For any x 1{0,1} n-1 Prob[X=x ] = 1/2n
Then H(X) = n/2+1/2
But Eve can cheat with probability at least ½ by
guessing that X=0n
Another Notion: Min Entropy
Let X be random variable over alphabet Γ with
distribution Px
The min entropy of X is
Hmin(X) = - log max x Γ Px (x)
The min entropy represents the most likely value of
X
Property: Hmin(X) ≤ H(X)
Why?
High Min Entropy and Passwords
Claim: if Alice and Bob agree on such that
Hmin(X) ≥ m, then the probability that Eve succeeds
in cheating is at most 2-m
Proof: Make Eve deterministic, by picking her best
choice, X’ = x’.
Prob[X=x’] = Px (x’) ≤ max x Γ Px (x) = 2 –Hmin(X) ≤ 2-m
Conclusion: passwords should be chosen to have
high min-entropy!
Good source on Information Theory:
T. Cover and J. A. Thomas, Elements of Information Theory
One-time vs. many times
• This was good for a single identification. What
about many identification?
• Later…
A different scenario – now Charlie is
involved
• Bob has no proof that Alice indeed identified
• If there are two possible verifiers, Bob and Charlie,
they can each pretend to each other to be Alice
– Can each have there own string
– But, assume that they share the setup phase
• Whatever Bob knows Charlie know
• Relevant when they are many of possible verifiers!
The new requirement
• If Alice wants to approve and Eve does not interfere
– Bob moves to state Y
• If Alice does not approve, then for any behavior
from Eve and Charlie, Bob stays in N
• Similarly if Bob and Charlie are switched
Charlie
Alice
Bob
Eve
Can we achieve the requirements?
• Observation: what Bob and Charlie received in the setup
phase might as well be public
• Therefore can reduce to the previous scenario (with no
setup)…
• To the rescue - complexity
Alice should be able to perform something that neither Bob
nor Charlie (nor Eve) can do
Must assume that the parties are not
computationally all powerful!
Function and inversions
• We say that a function f is hard to invert if given y=f(x) it
is hard to find x’ such that y=f(x’)
– x’ need not be equal to x
– We will use f-1(y) to denote the set of preimages of y
• To discuss hard must specify a computational model
• Use two flavors:
– Concrete
– Asymptotic
One-way functions - asymptotic
A function f: {0,1}* → {0,1}* is called a one-way function, if
• f is a polynomial-time computable function
– Also polynomial relationship between input and output length
• for every probabilistic polynomial-time algorithm A, every positive
polynomial p(.), and all sufficiently large n’s
Prob[A[f(x)]  f-1(f(x)) ] ≤ 1/p(n)
Where x is chosen uniformly in {0,1}n and the probability is also over
the internal coin flips of A
One-way functions – concrete version
A function f:{0,1}n → {0,1}n is called a (t,ε) one-way
function, if
• f is a polynomial-time computable function (independent of t)
• for every t-time algorithm A,
Prob[A[f(x)]  f-1(f(x)) ] ≤ ε
Where x is chosen uniformly in {0,1}n and the probability is also
over the internal coin flips of A
Can either think of t and ε as being fixed or as t(n), ε(n)
Complexity Theory and One-way Functions
• Claim: if P=NP then there are no one-way functions
• Proof: for any one-way function
f: {0,1}n → {0,1}n
consider the language Lf :
– Consisting of strings of the form {y, b1, b2…bk}
– There is an x  {0,1}n such that y=f(x) and
– The first k bits of x are b1, b2…bk
Lf is NP – guess x and check
If Lf is P then f is invertible in polynomial time:
Self reducibility
A few properties and questions concerning
one-way functions
• Major open problem: connect the existence of one-way functions and
the P=NP? question
• If f is one-to-one it is a called a one-way permutation. In what
complexity class does the problem of inverting one-way permutations
reside?
– good exercise!
• If f’ is a one-way function, is f’ where f’(x) is f(x) with the last bit
chopped a one-way function?
• If f is a one-way function, is fL where fL(x) consists of the first half of
the bits of f(x) a one-way function?
– good exercise!
• If f is a one way function is g(x) = f(f(x)) necessarily a one-way
function?
– good exercise!
Solution to the password problem
• Assume that
– f: {0,1}n → {0,1}n is a (t,ε) one-way function
– Adversary’s run times is bounded by t
• Setup phase:
– Alice chooses xR {0,1}n
– computes y=f(x)
– Gives y to Bob and Charlie
• When Alice wants to approve – she sends x
• If Bob gets any symbols on channel – call them z; compute
f(z) and compares to y
– If equal moves to state Y
– If not equal moves permanently to state N
Eve’s and Charlie’s probability of success
•
If Alice did not send x and Eve (Charlie) put some string x’ on the channel to Bob, then:
– Bob moves to state Y only if f(x’)=y=f(x)
– But we know that
Prob[A[f(x)]  f-1(f(x)) ] ≤ ε
or else we can use Eve to break the one-way function
A’
y
Eve yy
x’
x’
Good news: if ε can be made as small as we wish, then we have a good scheme.
•
•
Can be used for monitoring
Similar to the Unix password scheme
– f(x) stored in login file
– DES used as the one-way function.
Reductions
• This is a simple example of a reduction
• Simulate Eve’s algorithm in order to break the oneway function
• Most reductions are much more involved
Cryptographic Reductions
Show how to use an adversary for breaking primitive 1
in order to break primitive 2
Important
• Run time: how does T1 relate to T2
• Probability of success: how does 1 relate to 2
• Access to the system 1 vs. 2
Are one-way functions essential to the two
guards password problem?
• Precise definition:
– for every probabilistic polynomial-time algorithm A controlling Eve
and Charlie
– every polynomial p(.),
– and all sufficiently large n’s
Prob[Bob moves Y | Alice does not approve] ≤ 1/p(n)
• Recall observation: what Bob and Charlie received in the
setup phase might as well be public
• Claim: can get rid of interaction:
– given an interactive identification protocol possible to construct a
noninteractive one. In new protocol:
• Alice’ sends Bob’ the random bits Alice used to generate the setup information
• Bob’ simulates the conversation between Alice and Bob in original protocol and
accepts only if simulated Bob accepts.
• Probability of cheating is the same
One-way functions are essential to the two
guards password problem
• Are we done? Given a noninteracive identification protocol
want to define a one-way function
• Define function f(r) as the mapping that Alice does in the
setup phase between her random bits r and the information y
given to Bob and Charlie
• Problem: the function f(r) is not necessarily one-way…
– Can be unlikely ways to generate it. Can be exploited to invert.
– Example: Alice chooses x, x’ {0,1}n if x’= 0n set y=x o.w. set
y=f(x)
– The protocol is still secure, but with probability 1/2n not complete
– The resulting function f(x,x’) is easy to invert:
• given y {0,1}n set inverse as (y, 0n )
One-way functions are essential to the two
guards password problem…
• However: possible to estimate the probability that Bob
accepts on a given string from Alice
• Second attempt: define function f(r) as
– the mapping that Alice does in the setup phase between
her random bits r and the information given to Bob and
Charlie,
– plus a bit indicating that probability of Bob accepts given
r is greater than 2/3
Theorem: the two guards password problem has a
solution if and only if one-way functions exist
Examples of One-way functions
Examples of hard problems:
• Subset sum
• Discrete log
• Factoring (numbers, polynomials) into prime
components
Easy problem
How do we get a one-way function out of them?
Subset Sum
•
Subset sum problem: given
•
(n,m)-subset sum assumption: for uniformly chosen
– n numbers 0 ≤ a1, a2 ,…, an ≤ 2m
– Target sum T
– Find subset S⊆ {1,...,n} ∑ i S ai,=T
– a1, a2 ,…, an R{0,…2m -1} and S⊆ {1,...,n}
– For any probabilistic polynomial time algorithm, the probability of finding S’⊆ {1,...,n} such
that
∑ i S ai= ∑ i S’ ai
is negligible, where the probability is over the random choice of the ai‘s, S and the inner coin
flips of the algorithm
•
Subset sum one-way function f:{0,1}mn+n → {0,1}m
f(a1, a2 ,…, an , b1, b2 ,…, bn ) =
(a1, a2 ,…, an , ∑ i=1n bi ai mod 2m )
Exercise
• Show a function f such that
– if f is polynomial time invertible on all inputs, then P=NP
– f is not one-way
Discrete Log Problem
• Let G be a group and g an element in G.
• Let y=gz and x the minimal non negative
integer satisfying the equation.
x is called the discrete log of y to base g.
• Example: y=gx mod p in the multiplicative group of Zp
• In general: easy to exponentiate via repeated squaring
– Consider binary representation
• What about discrete log?
– If difficult, f(g,x) = (g, gx ) is a one-way function
Integer Factoring
• Consider f(x,y) = x • y
• Easy to compute
• Is it one-way?
– No: if f(x,y) is even can set inverse as (f(x,y)/2,2)
• If factoring a number into prime factors is hard:
– Specifically given N= P • Q , the product of two random large (n-bit) primes, it
is hard to factor
– Then somewhat hard – there are a non-negligible fraction of such numbers ~
1/n2 from the density of primes
– Hence a weak one-way function
• Alternatively:
– let g(r) be a function mapping random bits into random primes.
– The function f(r1,r2) = g(r1) • g(r2) is one-way
Weak One-way function
A function f: {0,1}n → {0,1}n is called a weak one-way
function, if
• f is a polynomial-time computable function
• There exists a polynomial p(¢), for every probabilistic
polynomial-time algorithm A, and all sufficiently large n’s
Prob[A[f(x)]  f-1(f(x)) ] ≤ 1-1/p(n)
Where x is chosen uniformly in {0,1}n and the probability is
also over the internal coin flips of A
Exercise: weak exist if strong exists
Show that if strong one-way functions exist, then
there exists a a function which is a weak one-way
function but not a strong one
What about the other direction?
• Given
– a function f that is guaranteed to be a weak one-way
• Let p(n) be such that Prob[A[f(x)]  f-1(f(x)) ] ≤ 1-1/p(n)
– can we construct a function g that is (strong) one-way?
An instance of a hardness amplification problem
• Simple idea: repetition. For some polynomial q(n) define
g(x1, x2 ,…, xq(n) )=f(x1), f(x2), …, f(xq(n))
• To invert g need to succeed in inverting f in all q(n)
places
– If q(n) = p2(n) seems unlikely (1-1/p(n))p2(n) ≈ e-p(n)
– But how to we show? Sequential repetition intuition – not a proof.
Want: Inverting g with low probability
implies inverting f with high probability
• Given a machine A that inverts g want a machine A’
– operating in similar time bounds
– inverts f with high probability
• Idea: given y=f(x) plug it in some place in g and generate the rest
of the locations at random
z=(y, f(x2), …, f(xq(n)))
• Ask machine A to invert g at point z
• Probability of success should be at least (exactly) A’s Probability of
inverting g at a random point
• Once is not enough
• How to amplify?
– Repeat while keeping y fixed
– Put y at random position (or sort the inputs to g )
Proof of Amplification for Repetition of Two
• Concentrate on repetition of two g(x1, x2 )=f(x1), f(x2)
• Goal: show that the probability of inverting g is roughly squared the
probability of inverting f
just as would be sequentially
• Claim:
Let (n) be a function that for some p(n) satisfies
1/p(n) ≤ (n) ≤ 1-1/p(n)
Let ε(n) be any inverse polynomial function
suppose that for every polynomial time A and sufficiently large n
Prob[A[f(x)]  f-1(f(x)) ] ≤ (n)
Then for every polynomial time B and sufficiently large n
Prob[B[g(x1, x2 )]  g-1(g(x1, x2 )) ] ≤ 2(n) + ε(n)
Proof of Amplification for Two Repetition
Suppose not, then given a better than 2+ε algorithm
B for inverting g construct the following:
• B’(y) Inversion algorithm for f
– Repeat t times
•
•
•
•
Choose x’ at random and compute y’=f(x’)
Run B(y,y’).
Check the results
Helpful for
constructive
If correct: Halt with success
– Output failure
algorithm
Inner
loop
Probability of Success
• Define
S={y=f(x) | Prob[Inner loop successful| y ] > β}
• Since the choices of the x’ are independent
Prob[B’ succeeds| xS] > 1-(1- β)t
Taking t= n/β means that when yS almost surely A will
invert it
• Hence want to show that Prob[ yS] > (n)
The success of B
• Fix the random bits of B. Define
P={(y1, y2)| B succeeds on (y1,y2)}
P= P ⋂ {(y1,y2 )| y1,y2 S}
⋃ P ⋂ {(y1,y2 )| y1 S}
y1
⋃ P ⋂ {(y1,y2 )| y2 S}
Well behaved
part
y2
P
want to bound P by
a square
S is the only success..
But
Prob[B[y1, y2]  g-1(y1, y2) | y1 S] ≤ β
and similarly
Prob[B[y1, y2]  g-1(y1, y2) | y2 S] ≤ β
so
Prob[(y1, y2) P and y1,y2 S]
≥ Prob[(y1, y2) P ] - 2β
≥ 2+
ε - 2β
Setting β =ε/3 we have
Prob[(y1, y2) P and y1,y2 S] ≥ 2+
ε/3
Contradiction
But
Prob[(y1, y2) P and y1,y2 S]
≤ Prob[y1 S] Prob[y2 S]
= Prob2[y S]
So
Prob[y S] ≥ √(α2+ ε/3) > α
The Encryption problem:
• Alice would want to send a message m  {0,1}n
to Bob
– Set-up phase is secret
• They want to prevent Eve from learning anything
about the message
m
Alice
Eve
Bob
The encryption problem
• Relevant both in the shared key and in the public
key setting
• Want to use many times
• Also add authentication…
• Other disruptions by Eve
What does `learn’ mean?
• If Eve has some knowledge of m should remain the same
– Probability of guessing m
• Min entropy of m
– Probability of guess whether m is m0 or m1
– Probability of computing some function f of m
• Ideally: the message sent is a independent of the message m
– Implies all the above
• Shannon: achievable only if the entropy of the shared secret is at least
as large as the message m entropy
• If no special knowledge about m
– then |m|
• Achievable: one-time pad.
–
–
–
–
Let rR {0,1}n
Think of r and m as elements in a group
To encrypt m send r+m
To decrypt z send m=z-r
Pseudo-random generators
• Would like to stretch a short secret (seed) into a long one
• The resulting long string should be usable in any case
where a long string is needed
– In particular: as a one-time pad
• Important notion: Indistinguishability
Two probability distributions that cannot be distinguished
– Statistical indistinguishability: distances between probability
distributions
– New notion: computational indistinguishability
...References
Books:
• O. Goldreich, Foundations of Cryptography - a book in
three volumes.
– Vol 1, Basic Tools, Cambridge, 2001
• Pseudo-randomness, zero-knowledge
– Vol 2, about to come out
• (Encryption, Secure Function Evaluation)
– Other volumes in www.wisdom.weizmann.ac.il/~oded/books.html
• M. Luby, Pseudorandomness and Cryptographic
Applications, Princeton University Pres
References
Web material/courses
• S. Goldwasser and M. Bellare, Lecture Notes on
Cryptography,
http://www-cse.ucsd.edu/~mihir/papers/gb.html
• Wagner/Trevisan, Berkeley
www.cs.berkeley.edu/~daw/cs276
• Ivan Damgard and Ronald Cramer, Cryptologic Protocol
Theory
http://www.daimi.au.dk/~ivan/CPT.html
• Salil Vadhan, Pseudorandomness
– http://www.courses.fas.harvard.edu/~cs225/Lectures-2002/
• Naor, Foundations of Cryptography and Estonian Course
– www.wisdom.weizmann.ac.il/~naor
Recap of Lecture 1
• Key idea of cryptography: use computational
intractability for your advantage
• One-way functions are necessary and sufficient to
solve the two guard identification problem
– Notion of Reduction between cryptographic primitives
• Amplification of weak one-way functions
– Things are a bit more complex in the computational
world (than in the information theoretic one)
Is there an ultimate one-way function?
• If f1:{0,1}* → {0,1}* and f2:{0,1}* → {0,1}* are guaranteed to:
– Be polynomial time computable
– At least one of them is one-way.
then can construct a function g:{0,1}* → {0,1}* which is one-way:
g(x1, x2 )= (f1(x1),f2 (x2 ))
• If an 5n2 time one-way function is guaranteed to exist, can construct
an O(n2 log n) one-way function g:
– Idea: enumerate Turing Machine and make sure they run 5n2 steps
g(x1, x2 ,…, xlog (n) )=M1(x1), M2(x2), …, Mlog n(xlog (n))
• If a one-way function is guaranteed to exist, then there exists a 5n2
time one-way:
– Idea: concentrate on the prefix
1/p(n)
Conclusions
• Be careful what you wish for
• Problem with resulting one-way function:
– Cannot learn about behavior on large inputs from small inputs
– Whole rational of considering asymptotic results is eroded
• Construction does not work for non-uniform one-way
functions
• Encryption: easy when you share very long strings
• Started with the notion of pseudo-randomness
The Encryption problem:
• Alice would want to send a message m  {0,1}n
to Bob
– Set-up phase is secret
• They want to prevent Eve from learning anything
about the message
m
Alice
Eve
Bob
The encryption problem
• Relevant both in the shared key and in the public
key setting
• Want to use many times
• Also add authentication…
• Other disruptions by Eve
What does `learn’ mean?
• If Eve has some knowledge of m should remain the same
– Probability of guessing m
• Min entropy of m
– Probability of guess whether m is m0 or m1
– Probability of computing some function f of m
• Ideally: the message sent is a independent of the message m
– Implies all the above
• Shannon: achievable only if the entropy of the shared secret is at least
as large as the message m entropy
• If no special knowledge about m
– then |m|
• Achievable: one-time pad.
–
–
–
–
Let rR {0,1}n
Think of r and m as elements in a group
To encrypt m send r+m
To decrypt z send m=z-r
Pseudo-random generators
• Would like to stretch a short secret (seed) into a long one
• The resulting long string should be usable in any case
where a long string is needed
– In particular: as a one-time pad
• Important notion: Indistinguishability
Two probability distributions that cannot be distinguished
– Statistical indistinguishability: distances between probability
distributions
– New notion: computational indistinguishability
Computational Indistinguishability
Definition: two sequences of distributions {Dn} and {D’n} on
{0,1}n are computationally indistinguishable if
for every polynomial p(n) and sufficiently large n, for every probabilistic
polynomial time adversary A that receives input y  {0,1}n and
tries to decide whether y was generated by Dn or D’n
|Prob[A=‘0’ | Dn ] - Prob[A=‘0’ | D’n ] | < 1/p(n)
Without restriction on probabilistic polynomial tests: equivalent to
variation distance being negligible
∑β  {0,1}n |Prob[ Dn = β] - Prob[ D’n = β]| < 1/p(n)
Pseudo-random generators
Definition: a function g:{0,1}* → {0,1}* is said to be a (cryptographic) pseudo-random
generator if
• It is polynomial time computable
• It stretches the input |g(x)|>|x|
–
•
denote by ℓ(n) the length of the output on inputs of length n
If the input (seed) is random, then the output is indistinguishable from random
For any probabilistic polynomial time adversary A that receives input y of length ℓ(n)
and tries to decide whether y= g(x) or is a random string from {0,1}ℓ(n) for any
polynomial p(n) and sufficiently large n
|Prob[A=`rand’| y=g(x)] - Prob[A=`rand’| yR {0,1}ℓ(n)] | < 1/p(n)
Want to use the output a pseudo-random generator whenever long random strings are used
Especially encryption
– have not defined the desired properties yet.
Anyone who considers arithmetical methods of producing random numbers is, of course, in a
state of sin.
J. von Neumann
Important issues
• Why is the adversary bounded by polynomial time?
• Why is the indistinguishability not perfect?
Construction of pseudo-random generators
• Idea: given a one-way function there is a hard
decision problem hidden there
• If balanced enough: looks random
• Such a problem is a hardcore predicate
• Possibilities:
– Last bit
– First bit
– Inner product
Hardcore Predicate
Definition: let f:{0,1}* → {0,1}* be a function. We say that h:{0,1}*
→ {0,1} is a hardcore predicate for f if
• It is polynomial time computable
• For any probabilistic polynomial time adversary A that receives input
y=f(x) and tries to compute h(x) for any polynomial p(n) and
sufficiently large n
|Prob[A(y)=h(x)] -1/2| < 1/p(n)
where the probability is over the choice y and the random coins of A
• Sources of hardcoreness:
– not enough information about x
• not of interest for generating pseudo-randomness
– enough information about x but hard to compute it
Exercises
Assume one-way functions exist
• Show that the last bit/first bit are not necessarily hardcore
predicates
• Generalization: show that for any fixed function h:{0,1}*
→ {0,1} there is a one-way function f:{0,1}* → {0,1}*
such that h is not a hardcore predicate of f
• Show a one-way function f such that given y=f(x) each
input bit of x can be guessed with probability at least 3/4
Single bit expansion
• Let f:{0,1}n → {0,1}n be a one-way permutation
• Let h:{0,1}n → {0,1} be a hardcore predicate for
f
• Consider g:{0,1}n → {0,1}n+1 where
g(x)=(f(x), h(x))
Claim: g is a pseudo-random generator
Proof: can use a distinguisher for g to guess h(x)
f(x), h(x))
f(x), 1-h(x))
Hardcore Predicate With Public Information
Definition: let f:{0,1}* → {0,1}* be a function. We say that h:{0,1}* x
{0,1}* → {0,1} is a hardcore predicate for f if
• h(x,r) is polynomial time computable
• For any probabilistic polynomial time adversary A that receives input
y=f(x) and public randomness r and tries to compute h(x,r) for any
polynomial p(n) and sufficiently large n
|Prob[A(y,r)=h(x,r)] -1/2| < 1/p(n)
where the probability is over the choice y of r and the random coins of A
Alternative view: can think of the public randomness as modifying the
one-way function f: f’(x,r)=f(x),r.
Example: weak hardcore predicate
• Let h(x,i)= xi
I.e. h selects the ith bit of x
• For any one-way function f, no polynomial time algorithm A(y,i)
can have probability of success better than 1-1/2n of computing
h(x,i)
• Exercise: let c:{0,1}* → {0,1}* be a good error correcting code
– |c(x)| is O(|x|)
– distance between any two codewords c(x) and c(x’) is a constant fraction of
|c(x)|
• It is possible to correct in polynomial time errors in a constant fraction of |c(x)|
Show that for h(x,i)= c(x)i and any one-way function f, no
polynomial time algorithm A(y,i) can have probability of success
better than a constant of computing h(x,i)
Inner Product Hardcore bit
• The inner product bit: choose r R {0,1}n let
h(x,r) = r ∙x = ∑ xi ri mod 2
Theorem [Goldreich-Levin]: for any one-way function the inner product
is a hardcore predicate
Proof structure:
• There are many x’s for which A returns a correct answer on ½+ε of
the r ’s
• take an algorithm A that guesses h(x,r) correctly with probability
½+ε over the r‘s and output a list of candidates for x
– No use of the y info
• Choose from the list the/an x such that f(x)=y
The main
step!
Why list?
• Cannot have a unique answer!
• Suppose A has two candidates x and x’
– On query r it returns at `random’ either r ∙x or r ∙x’
Prob[A(y,r) = r ∙x ] =½ +½Prob[r∙x = r∙x’] = ¾
Warm-up (1)
If A returns a correct answer on 1-1/2n of the r ’s
• Choose r1, r2, … rn R {0,1}n
• Run A(y,r1), A(y,r2), … A(y,rn)
– Denote the response z1, z2, … zn
• If r1, r2, … rn are linearly independent then:
there is a unique x satisfying ri∙x = zi for all 1 ≤i ≤n
• Prob[zi = A(y,ri)= ri∙x]≥ 1-1/2n
– Therefore probability that all the zi‘s are correct is at least ½
– Do we need complete independence of the ri ‘s?
• `one-wise’ independence is sufficient
Can choose r R {0,1}n and set ri∙ = r+ei
ei =0i-110n-i
All the ri `s are linearly independent
Each one is uniform in {0,1}n
Warm-up (2)
If A returns a correct answer on 3/4+ε of the r ’s
Can amplify the probability of success!
Given any r  {0,1}n Procedure A’(y,r):
• Repeat for j=1, 2, …
– Choose r’ R {0,1}n
– Run A(y,r+r’) and A(y,r’), denote the sum of responses by zj
• Output the majority of the zj’s
Analysis
Pr[zj = r∙x]≥ Pr[A(y,r’)=r∙x ^ A(y,r+r’)=(r+r’)∙x]≥½+2ε
– Does not work for ½+ε since success on r’ and r+r’ is not independent
• Each one of the events ‘zj = r∙x’ is independent of the others
• Therefore by taking sufficiently many j’s can amplify to a value as
close to 1 as we wish
– Need roughly 1/ε2 examples
Idea for improvement: fix a few of the r’
The real thing
•
•
Choose r1, r2, … rk R {0,1}n
Guess for j=1, 2, … k the value zj =rj∙x
•
For all nonempty subsets S {1,…,k}
•
For each position xi
– Go over all 2k possibilities
– Let rS = ∑ j S rj
– The implied guess for zS = ∑ j S zj
– for each S {1,…,k} run A(y,ei-rS)
– output the majority value of {zs +A(y,ei-rS) }
Analysis:
• Each one of the vectors ei-rS is uniformly distributed
•
– A(y,ei-rS) is correct with probability at least ½+ε
Claim: For every pair of nonempty subset S ≠T {1,…,k}:
–
the two vectors rS and rT are pair-wise independent
•
Therefore variance is as in completely independent trials
•
Need 2k = n/ε2 to get the probability of error to 1/n
– I is the number of correct A(y,ei-rS), VAR(I) ≤ 2k(½+ε)
– Use Chebyshev’s Inequality Pr[|I-E(I)|≥ λ√VAR(I)]≤1/λ2
– So process is successful simultaneously for all positions xi,i{1,…,n}
S
T
Analysis
Number of invocations of A
• 2k ∙ n ∙ (2k-1) = poly(n, 1/ε) ≈ n3/ε4
Size of resulting list of candidates for x
guesses
positions
subsets
for each guess of z1, z2, … zk unique x
• 2k =poly(n, 1/ε) ) ≈ n/ε2
Conclusion: single bit expansion of a one-way permutation is
a pseudo-random generator
Reducing the size of the list of candidates
Idea: bootstrap
Given any r  {0,1}n Procedure A’(y,r):
• Choose r1, r2, … rk R {0,1}n
• Guess for j=1, 2, … k the value zj =rj∙x
– Go over all 2k possibilities
• For all nonempty subsets S {1,…,k}
– Let rS = ∑ j S rj
– The implied guess for zS = ∑ j S zj
– for each S {1,…,k} run A(y,r-rS)
• output the majority value of {zs +A(y,r-rS)
• For 2k = 1/ε2 the probability of error is, say, 1/8
Fix the same r1, r2, … rk for subsequent executions
They are good for 7/8 of the r’s
Run warm-up (2)
Size of resulting list of candidates for x is ≈ 1/ε2
Application: Diffie-Hellman
The Diffie-Hellman assumption
Let G be a group and g an element in G.
Given g, a=gx and b=gy it is hard to find c=gxy
for random x and y is probability of poly-time
machine outputting gxy is negligible
More accurately: a sequence of groups
• Don’t know how to verify given c’ whether
it is equal to gxy
• Exercise: show that under the DH
Assumption
Given a=gx , b=gy and r  {0,1}n no polynomial time
machine can guess r ∙gxy with advantage 1/poly
– for random x,y and r
Application: if subset is one-way, then it is a
pseudo-random generator
• Subset sum problem: given
– n numbers 0 ≤ a1, a2 ,…, an ≤ 2m
– Target sum y
– Find subset S⊆ {1,...,n} ∑ i S ai,=y
• Subset sum one-way function f:{0,1}mn+n → {0,1}m
f(a1, a2 ,…, an , x1, x2 ,…, xn ) =
(a1, a2 ,…, an , ∑ i=1n xi ai mod 2m )
If m<n then we get out less bits then we put in.
If m>n then we get out more bits then we put in.
Theorem: if for m>n subset sum is a one-way function, then it is
also a pseudo-random generator
Subset Sum Generator
Idea of proof: use the distinguisher A to compute r ∙x
For simplicity: do the computation mod P for large prime P
• Given r  {0,1}n and (a1, a2 ,…, an ,y)
Generate new problem(a’1, a’2 ,…, a’n ,y’) :
• Choose c R ZP
• Let a’i = ai if ri=0 and ai =ai+c mod P if ri=1
• Guess k R {o,…,n} - the value of ∑ xi ri
Prob[A=‘0’|pseudo]= ½+ε
Prob[A=‘0’|random]= ½
– the number of locations where x and r are 1
pseudorandom
• Let y’ = y+c k mod P
Run the distinguisher A on (a’1, a’2 ,…, a’n ,y’)
– output what A says Xored with parity(k)
Claim: if k is correct, then (a’1, a’2 ,…, a’n ,y’) is R pseudo-random
Claim: for any incorrect k, (a’1, a’2 ,…, a’n ,y’) is R random
y’= z + (k-h)c mod P where z = ∑ i=1n xi a’i mod P and h=∑ xi ri
random
Therefore: probability to guess correctly r ∙x is 1/n∙(½+ε) + (n-1)/n (½)= ½+ε/n
correct k
incorrect k
Interpretations of the Goldreich-Levin Theorem
• A tool for constructing pseudo-random generators
The main part of the proof:
• A mechanism for translating `general confusion’ into randomness
– Diffie-Hellman example
• List decoding of Hadamard Codes
– works in the other direction as well (for any code with good list decoding)
– List decoding, as opposed to unique decoding, allows getting much closer to
distance
• `Explains’ unique decoding when prediction was 3/4+ε
• Finding all linear functions agreeing with a function given in a blackbox
– Learning all Fourier coefficients larger than ε
• If the Fourier coefficients are concentrated on a small set – can find
them
– True for AC0 circuits
– Decision Trees
Composing PRGs
ℓ1
Composition
Let
• g1 be a (ℓ1, ℓ2 )-pseudo-random generator
• g2 be a (ℓ2, ℓ3)-pseudo-random generator
Consider g(x) = g2(g1(x))
Claim: g is a (ℓ1, ℓ3 )-pseudo-random generator
Proof: consider three distributions on {0,1}ℓ3
ℓ2
ℓ3
– D1: y uniform in {0,1}ℓ3
– D2: y=g(x) for x uniform in {0,1}ℓ1
– D3: y=g2(z) for z uniform in {0,1}ℓ2
By assumption there is a distinguisher A between D1 and D2
A must either
or
distinguish between D1 and D3
distinguish between D2 and D3
- can use A use to distinguish g2
- can use A use to distinguish g1
triangle inequality
Composing PRGs
When composing
• a generator secure against advantage ε1
and a
• a generator secure against advantage ε2
we get security against advantage ε1+ε2
When composing the single bit expansion generator n times
Loss in security is at most ε/n
Hybrid argument: to prove that two distributions D and D’ are
indistinguishable:
suggest a collection of distributions D= D0, D1,… Dk =D’ such that
If D and D’ can be distinguished, there is a pair Di and Di+1 that can
be distinguished.
Difference ε between D and D’ means ε/k between some Di and Di+1
Use such a distinguisher to derive a contradiction
Exercise
• Let {Dn} and {D’n} be two distributions that are
– Computationally indistinguishable
– Polynomial time samplable
• Suppose that {y1,… ym} are all sampled according to
{Dn} or all are sampled according to {D’n}
• Prove: no probabilistic polynomial time machine can tell,
given {y1,… ym}, whether they were sampled from
{Dn} or {D’n}
Existence of PRGs
What we have proved:
Theorem: if pseudo-random generators stretching by a single
bit exist, then pseudo-random generators stretching by any
polynomial factor exist
Theorem: if one-way permutations exist, then pseudo-random
generators exist
A harder theorem to prove
Theorem [HILL]: if one-way functions exist, then pseudorandom generators exist
Exercise: show that if pseudo-random generators exist, then
one-way functions exist
Next-bit Test
Definition: a function g:{0,1}* → {0,1}* is said to pass the next bit
test if
• It is polynomial time computable
• It stretches the input |g(x)|>|x|
– denote by ℓ(n) the length of the output on inputs of length n
• If the input (seed) is random, then the output passes the next-bit test
For any prefix 0≤ i< ℓ(n), for any probabilistic polynomial time adversary A that
receives the first i bits of y= g(x) and tries to guess the next bit, or any
polynomial p(n) and sufficiently large n
|Prob[A(yi,y2,…, yi)= yi+1] – 1/2 | < 1/p(n)
Theorem: a function g:{0,1}* → {0,1}* passes the next bit test if
and only if it is a pseudo-random generator
Next-block Undpredictable
Suppose that the function G maps a given a seed into a sequence of blocks
G:
y
y , … ,
1
2
S
let ℓ(n) be the length of the number of blocks given a seed of length n
• If the input (seed) is random, then the output passes the next-block
unpredicatability test
For any prefix 0≤ i< ℓ(n), for any probabilistic polynomial time adversary A that
receives the first i blocks of y= g(x) and tries to guess the next block yi+1, for any
polynomial p(n) and sufficiently large n
|Prob[A(y1,y2,…, yi)= yi+1] | < 1/p(n)
Exercise: show how to convert a next-block unpredictable generator into a
pseudo-random generator.
Pseudo-Random Generators
concrete version
Gn:0,1m 0,1n
A cryptographically strong pseudo-random sequence
generator - if passes all polynomial time statistical
tests
(t,)-pseudo-random - no test A running in time t
can distinguish with advantage 
Three Basic issues in cryptography
• Identification
• Authentication
• Encryption
Solve in a shared key environment
A
B
S
S
Identification - Remote login using
pseudo-random sequence
A and B share key S0,1k
In order for A to identify itself to B
• Generate sequence Gn(S)
G:
S
Gn(S)
• For each identification session - send next block of
Gn(S)
Problems...
•
•
•
•
More than two parties
Malicious adversaries - add noise
Coordinating the location block number
Better approach: Challenge-Response
Challenge-Response Protocol
• B selects a random location and sends to A
• A sends value at random location
A
B
What’s this?
Desired Properties
• Very long string - prevent repetitions
• Random access to the sequence
• Unpredictability - cannot guess the value at a random
location
– even after seeing values at many parts of the string to the
adversary’s choice.
– Pseudo-randomness implies unpredictability
• Not the other way around for blocks
Authenticating Messages
• A wants to send message M0,1n to B
• B should be confident that A is indeed the sender of M
One-time application:
S =(a,b) where a,bR 0,1n
To authenticate M: supply aM b
Computation is done in GF[2n]
Problems and Solutions
• Problems - same as for identification
• If a very long random string available – can use for one-time authentication
– Works even if only random looking
a,b
A
B
Use this!
Encryption of Messages
• A wants to send message M0,1n to B
• only B should be able to learn M
One-time application:
S=a
where aR 0,1n
To encrypt M:
send a  M
Encryption of Messages
• If a very long random looking string available – can use as in one-time encryption
A
B
Use this!
Pseudo-random Functions
Concrete Treatment:
F: 0,1k  0,1n  0,1m
key
Domain
Range
Denote Y= FS (X)
A family of functions Φk ={FS | S0,1k  is
(t, , q)-pseudo-random if it is
• Efficiently computable - random access
and...
(t,,q)-pseudo-random
The tester A that can choose adaptively
– X1 and get Y1= FS (X1)
– X2 and get Y2 = FS (X2 )
…
– Xq and get Yq= FS (Xq)
• Then A has to decide whether
– FS R Φk or
– FS R R n  m =  F | F :0,1n  0,1m 
(t,,q)-pseudo-random
For a function F chosen at random from
(1) Φk ={FS | S0,1k 
(2) R n  m =  F | F :0,1n  0,1m 
For all t-time machines A that choose q locations
and try to distinguish (1) from (2)
 ProbA ‘1’  FR Fk 
- ProbA ‘1’  FR R n  m    
Equivalent/Non-Equivalent Definitions
• Instead of next bit test: for XX1,X2 ,, Xq
chosen by A, decide whether given Y is
– Y= FS (X) or
– YR0,1m
• Adaptive vs. Non-adaptive
• Unpredictability vs. pseudo-randomness
• A pseudo-random sequence generator
g:0,1m 0,1n
– a pseudo-random function on small domain 0,1log n0,1
with key in 0,1m
Application to the basic issues in cryptography
Solution using a shared key S
Identification:
B to A: X R 0,1n
A to B: Y= FS (X)
A verifies
Authentication:
A to B: Y= FS (M)
replay attack
Encryption:
A chooses XR 0,1n
A to B: <X , Y= FS (X)  M >
Goal
• Construct an ensemble {Φk | kL  such that
• for any {tk, 1/k, qk | kL  polynomial in k, for
all but finitely many k’s
Φk is a (tk, k, qk )-pseudo-random family
Construction
• Construction via Expansion
– Expand n or m
• Direct constructions
Effects of Concatenation
Given ℓ Functions F1 , F2 ,, Fℓ decide whether they are
– ℓ random and independent functions
OR
– FS1 , FS2 ,, FSℓ for S1,S2 ,, Sℓ R0,1k
Claim: If Φk ={FS | S0,1k  is (t,,q)-pseudo-random:
cannot distinguish two cases
– using q queries
– in time t’=t - ℓq
– with advantage better than ℓ
Proof: Hybrid Argument
• i=0
• i
• i=ℓ
FS1 , FS2 ,, FSℓ
…
R1, R2 ,  , Ri-1,FSi , FSi+1 ,, FSℓ
…
R1, R2 ,  , Rℓ
 pℓ - p0  
  i pi+1 - pi  /ℓ
p0
pi
pℓ
...Hybrid Argument
Can use this i to distinguish whether
– FS R Φk or FS R R n  m
• Generate FSi+1 ,, FSℓ
• Answer queries to first i-1 functions at random (consistently)
• Answer query to FSi , using (black box) input
• Answer queries to functions i+1 through ℓ with FSi+1 ,, FSℓ
Running time of test - t’  ℓq
Doubling the domain
• Suppose F(n): 0,1k  0,1n  0,1m
which is (t,,q)-p.r.
• Want F(n+1): 0,1k  0,1n+1  0,1m
which is (t’,’,q’)-p.r.
Use G: 0,1k  0,12k which is (t ,) p.r
G(S)  G0(S) G1(S)
Let FS (n+1)(bx)  FGb(s) (n)(x)
Claim
If G is (tq,1)-p.r and F(n) is (t2q,2,q)-p.r, then
F(n+1) is (t,1 2 2,q)-p.r
Proof: three distributions
(1) F(n+1)
(2) FS0 (n) , FS1 (n) for independent S0, S1
(3) Random
 1 2 2
D
...Proof
Given that (1) and (3) can be distinguished with
advantage 1 2 2 , then either
• (1) and (2) with advantage 1
– G can be distinguished with advantage 1
or
• (2) and (3) with advantage 2 2
– F(n) can be distinguished with advantage 2
Running time of test - t’  q
Getting from G to F(n)
Idea: Use recursive construction
FS (n)(bnbn-1 b1)
 FGb (s) (n-1)(bn-1bn-2 b1)
1
 Gb (Gb (  Gb (S)) )
n
n-1
1
Each evaluation of FS (n)(x): n invocations of G
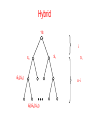
Tree Description
S
G0(S)
G1(S)
G0(G0(S))
G1(G0(G0(S)))
Each leaf corresponds to an X.
Label on leaf – value of pseudorandom function
Security claim
If G is (t qn ,) p.r,
then F(n) is (t, ’  nq,q) p.r
Proof: Hybrid argument by levels
Di :
– truly random labels for nodes at level i.
– Pseudo-random from i down
Each Di - a collection of q functions
 i pi+1 - pi  ’/n q
Hybrid
?S
i
S0
G0(S0)
S1
Di
n-i
G1(G0(S0))
…Proof of Security
• Can use this i to distinguish concatenation of q
sequence generators G from random.
• The concatenation is (t,q) p.r
Therefore the construction is (t,,q) p.r
Disadvantages
• Expensive - n invocations of G
• Sequential
• Deterioration of 
But does the job!
From any pseudo-random sequence generator construct a
pseudo-random function.
Theorem: one-way functions exist if and only if pseudrandom functions exist.
Applications of Pseudo-random
Functions
• Learning Theory - lower bounds
– Cannot PAC learn any class containing pseudo-random
function
• Complexity Theory - impossibility of natural proofs
for separating classes.
• Any setting where huge shared random string is
useful
• Caveat: what happens when the seed is made
public?
References
• Blum-Micali : SIAM J. Computing 1984
• Yao:
• Blum, Blum, Shub: SIAM J. Computing, 1988
• Goldreich, Goldwasser and Micali:
ACM, 1986
J. of the
...References
Books:
• O. Goldreich, Foundations of Cryptography - a book in
three volumes.
– Vol 1, Basic Tools, Cambridge, 2001
• Pseudo-randomness, zero-knowledge
– Vol 2, about to come out
• (Encryption, Secure Function Evaluation)
– Other volumes in www.wisdom.weizmann.ac.il/~oded/books.html
• M. Luby, Pseudorandomness and Cryptographic
Applications, Princeton University Pres
References
Web material/courses
• S. Goldwasser and M. Bellare, Lecture Notes on
Cryptography,
http://www-cse.ucsd.edu/~mihir/papers/gb.html
• Wagner/Trevisan, Berkeley
www.cs.berkeley.edu/~daw/cs276
• Ivan Damgard and Ronald Cramer, Cryptologic Protocol
Theory
http://www.daimi.au.dk/~ivan/CPT.html
• Salil Vadhan, Pseudorandomness
– http://www.courses.fas.harvard.edu/~cs225/Lectures-2002/
• Naor, Foundations of Cryptography and Estonian Course
– www.wisdom.weizmann.ac.il/~naor