Download Multilinear Formulas and Skepticism of Quantum Computing

Multilinear Formulas and Skepticism
of Quantum Computing

/
2


Scott Aaronson, UC Berkeley
“The Proving Of” Documentary
Trailers for Future Talks
Spanish Version
Announcements
Start Talk
Multilinear Formulas and Skepticism
of Quantum Computing

/
2


Scott Aaronson, UC Berkeley
“The Proving Of” Documentary
Trailers for Future Talks
Spanish Version
Announcements
Start Talk
Multilinear Formulas and Skepticism
of Quantum Computing

/
2


Scott Aaronson, UC Berkeley
“The Proving Of” Documentary
Trailers for Future Talks
Spanish Version
Announcements
Start Talk
Multilinear Formulas and Skepticism
of Quantum Computing

/
2


Scott Aaronson, UC Berkeley
“The Proving Of” Documentary
Trailers for Future Talks
Spanish Version
Announcements
Start Talk
Live Coverage of QIP’2004
http://fortnow.com/lance/complog
Multilinear Formulas and Skepticism
of Quantum Computing

/
2


Scott Aaronson, UC Berkeley
“The Proving Of” Documentary
Trailers for Future Talks
Spanish Version
Announcements
Start Talk
Four Objections to Quantum
Computing
Theoretical
Practical
Physical
(A): QC’s can’t
be built for
fundamental
reason
(B): QC’s can’t
be built for
engineering
reasons
Algorithmic
(C): Speedup
is of limited
theoretical
interest
(D): Speedup
is of limited
practical value
(A): QC’s can’t be built for fundamental
reason—Levin’s arguments
(1) Analogy to unit-cost arithmetic model
(2) Error-correction and fault-tolerance address
only relative error in amplitudes, not absolute
(3) “We have never seen a physical law valid to
over a dozen decimals”
(4) If a quantum computer failed, we couldn’t
measure its state to prove a breakdown of
QM—so no Nobel prize
“The present attitude is analogous to, say, Maxwell
selling the Daemon of his famous thought experiment as
a path to cheaper electricity from heat”
Responses
(1) Continuity in amplitudes more benign than in
measurable quantities—should we dismiss
classical probabilities of order 10-1000?
(2) How do we know QM’s successor won’t lift us to
PSPACE, rather than knock us down to BPP?
(3) To falsify QM, would suffice to show QC is in
some state far from eiHt|. E.g. Fitch & Cronin
won 1980 Physics Nobel “merely” for showing CP
symmetry is violated
Real Question: How far should we extrapolate from
today’s experiments to where QM hasn’t been tested?
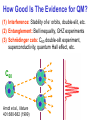
How Good Is The Evidence for QM?
(1) Interference: Stability of e- orbits, double-slit, etc.
(2) Entanglement: Bell inequality, GHZ experiments
(3) Schrödinger cats: C60 double-slit experiment,
superconductivity, quantum Hall effect, etc.
C60
Arndt et al., Nature
401:680-682 (1999)
Alternatives to QM
Roger Penrose
Gerard ‘t Hooft
(+ King of Sweden)
Stephen Wolfram
Exactly what property separates
the Sure States we know we can
create, from the Shor States that
suffice for factoring?
DIVIDING LINE
AmpP
I hereby
propose a
complexity
theory of pure
quantum
states n
Circuit
Tree
P
TSH
OTree
  H2
Vidal
MOTree
one of whose
goals is to
study possible
Sure/Shor
separators.

2
2
1
1
Strict containment
Containment
Non-containment
Classical
Boring Bonus Feature: Relations
Between Computational and Quantum
State Complexity Questions
BQP = P#P
implies
AmpP  P
AmpP  P
implies
NP  BQP/poly
P = P#P
implies
P  AmpP
P  AmpP
implies
BQP  P/poly
Tree size TS(|) = minimum number of unbounded-fanin
+ and  gates, |0’s, and |1’s needed in a tree
representing |. Constants are free. Permutation order
of qubits is irrelevant.
Tree states are states with polynomially-bounded TS
Example:
   00  2 01  10  11  / 7 
+
2
7

3
7

1
2
|01
+
1
2
|11

1
2
|02
+
1
2
|12
|01
|12
 TS  
  11
Multilinear Formulas
Trees involving +,, x1,…,xn, and complex
constants, such that every vertex computes a
multilinear polynomial (no xi multiplied by itself)
Given f : 0,1  , let MFS(f) be minimum
number of vertices in multilinear formula for f
n
+
Theorem: If

 

then
x1
x2
-3i
x1
TS  

x0,1
f  x  x ,
n
    MFS  f 
Grab Bag of Theorems
Theorem 1: Any tree state has a tree of polynomial
size and logarithmic depth
Theorem 2: Any orthogonal tree state (where all
additions are of orthogonal states) can be prepared by
a polynomial-size quantum circuit
Theorem 3: Most quantum states can’t even be
approximated by a state with subexponential tree size
Theorem 4: A quantum computer whose state is
always a tree state can be simulated in the 3rd level of
the classical polynomial-time hierarchy. Yields weak
evidence that TreeBQP  BQP
Coset States
Let C be a coset in
n
2
; then C  1
C
x
xC
Codewords of stabilizer codes (Gottesman,
Calderbank-Shor-Steane)
Take the following distribution over cosets: choose
A  Z 2k n , b  Z 2k uniformly at random (where
k=n1/3), then let C  x  Z n : Ax  b

2

Lower Bound To Be Proven:
 log n

   1
Pr TS  C   n
C
Raz’s Breakthrough
Given coset C, let
 1 if x  C
f  x  
0 otherwise
Need to lower-bound multilinear formula size
MFS(f)
Until June, superpolynomial lower bounds on MFS
didn’t exist
Raz: n(log n) MFS lower bounds for Permanent and
Determinant of nn matrix
(Exponential bounds conjectured, but n(log n) is the best Raz’s
method can show)
Cartoon of Raz’s Method
Given f : 0,1  , choose 2k input bits u.a.r.
Label them y1,…,yk, z1,…,zk
n
Randomly restrict remaining bits to 0 or 1 u.a.r.
Yields a new function f R  y, z  : 0,1  0,1 
k
Let
MR =
fR(y,z)
z{0,1}k
k
ALL QUESTIONS
WILL BE
ANSWERED BY
THE NEXT TALK
y{0,1}k
Theorem:
Pr  rank  M R   c2    1  MFS  f   n
k
 log n 
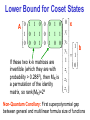
Lower Bound for Coset States
0 x
0
1
1
0
0
0
1
0


A
1 0 1 1 0 1 1 1   y1 

 
0 0 0 1 0 1 0 0  y2  1 
 
b
y
 3   1 
 


1
If these two kk matrices are
  0 
invertible (which they are with
 z1 
probability > 0.2882), then MR is  z 
2


a permutation of the identity
 z3 
matrix, so rank(M )=2k
R
Non-Quantum Corollary: First superpolynomial gap
between general and multilinear formula size of functions
Inapproximability of Coset States
Fact: For an NN complex matrix M=(mij),
rank  M   N   mij   ij
2
ij
(Follows from Hoffman-Wielandt inequality)
Corollary: With (1) probability over coset C, no
state | with TS(|)=no(log n) has ||C|20.98
Shor States
Superpositions over binary integers in arithmetic
progression: letting w = (2n-a-1)/p,
a p
1 w

a  pi

w i 0
(= 1st register of Shor’s alg after 2nd register is measured)
Theorem: Assuming a number-theoretic conjecture,
there exist p,a for which TS(|pZ+a)=n(log n)
Bonus Feature: My original conjecture
has been falsified by Carl Pomerance
Revised Conjecture (Not Yet
Falsified & Obviously True)
Let A consist of 5+log(n1/3) subsets of {20,…,2n-1}
chosen uniformly at random. For all 32n1/3 subsets B
of A, let S contain the sum of the elements of B. Let
S mod p = {x mod p : xS}. If p is chosen uniformly
at random from [n1/3,1.1n1.3], then
Prp [|S mod p|  3n1/3/4]  3/4
Theorem: Assuming this conjecture, quantum states
that arise in Shor’s algorithm have tree size n(log n)
Partial results toward proving the revised conjecture
by Don Coppersmith
Bonus Feature: Cluster States
Equal superposition over all settings of qubits in a
nn lattice, with phase=(-1)m where m is the
number of pairs of neighboring ‘1’ qubits
0 0 1 0 1
0 1 1 1 0
0 0 1 1 1
1 0 1 0 0
1 0 0 1 1
Conjecture: Cluster states have superpolynomial
tree size
Bonus Feature: Terhal States
Given an nn unitary matrix U and string x1…xn
with Hamming weight k, let Ux be the kk submatrix
of U formed by the first k rows and the columns
corresponding to xi=1. Then a Terhal state is

x0,1 : x  k
det U x  x
n
(Amazingly, these are always normalized)
Conjecture: Terhal states have superpolynomial
tree size
Challenge for Experimenters
• Create a uniform superposition over a
n
“generic” coset of 2 (n9) or even
better, Clifford group state
• Worthwhile even if you don’t
demonstrate error correction
• We’ll overlook that it’s really (1-10-5)I/512 + 10-5|CC|
New test of QM: are all states tree states?
What’s been done: 5-qubit codeword in liquid NMR
(Knill, Laflamme, Martinez, Negrevergne, quant-ph/0101034)
1  00000  10010  01001  10100  01010  11011  00110  11000
  
4   11101  00011  11110  01111  10001  01100  10111  00101
TS(|)  69



Tree Size Upper Bounds for Coset States
log2(# of nonzero amplitudes)
0
1
n 1
1
3
2
3
7
7
3
4
9
17
10
4
5
11
21
27
13
5
6
13
25
49
33
16
6
7
15
29
57
77
39
19
7
8
17
33
65
121 89
45
8
9
19
37
73
145 185 101 51
9
10
21
41
81
161 305 225 113 57
10
11
23
45
89
177 353 433 249 125 63
11
12
25
49
97
193 385 705 545 273 137 69
12
13
27
53
105 209 417 833 993 593 297 149 75
#
o
f
q
u
b
i
t
s
2
3
4
5
6
7
8
9
10
11
12
“Hardest” cases
(to left, use naïve
strategy; to right,
Fourier strategy)
22
25
28
31
34
37
For Clifford Group States
log2(# of nonzero amplitudes)
0
1
n 1
1
3
2
3
7
11
3
4
9
17
25
4
5
11
21
41
53
5
6
13
25
49
89
6
7
15
29
57
113 153 133
7
8
17
33
65
129 225 233 189
8
9
19
37
73
145 289 369 345 301
9
10
21
41
81
161 321 545 561 537 413
10
11
23
45
89
177 353 705 865 817 793 541
11
12
25
49
97
193 385 769
1281
1313
1265
1177
733
12
13
27
53
105 209 417 833
1665
1985
1889
1841
1689
#
o
f
q
u
b
i
t
s
2
3
4
5
6
7
8
9
10
11
12
85
957
Open Problems
• Exponential tree-size lower bounds
• Lower bound for Shor states
• Explicit codes (i.e. Reed-Solomon)
• Concrete lower bounds for (say) n=9
Important for
experiments
• Extension to mixed states
• Separate tree states and orthogonal tree states
• PAC-learn multilinear formulas? TreeBQP=BPP?
• Non-tree states already created?