* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Introduction to the Engineering Design Process
Survey
Document related concepts
Four-dimensional space wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
Line (geometry) wikipedia , lookup
Affine connection wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
CR manifold wikipedia , lookup
Lie derivative wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Cross product wikipedia , lookup
Tensor operator wikipedia , lookup
Curvilinear coordinates wikipedia , lookup
Metric tensor wikipedia , lookup
Tensors in curvilinear coordinates wikipedia , lookup
Transcript
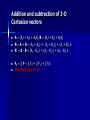
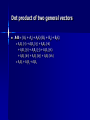
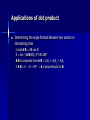
Scalars A scalar is any physical quantity that can be completely characterized by its magnitude (by a number value) Mathematical operations involving scalars – follow rules of elementary algebra In text represented with letters in italic type Examples: mass, volume, length Vectors Possess a magnitude, direction, and sense Represented graphically by an arrow (tail, tip or head) SHOW – Magnitude: proportional to the length of arrow – Direction: defined by angle between reference axis and line of action of the arrow – Sense: indicated by the arrowhead In text, vector symbolized by boldface type, A, and its magnitude (always positive) by |A | or simply A In slides, vector symbolized by boldface type, A, and magnitude by regular type, A In handwritten work, vector represented by letter with an arrow over it, its magnitude by letter enclosed in absolute value symbol or by letter itself SHOW Obey parallelogram law of addition Examples: position, force, moment Multiplication and division of a vector by a scalar Product of a vector, A, and a scalar, a – Vector, aA – Magnitude, aA – Sense of aA is the same as A provided a is positive, it is opposite to A if a is negative Division can be converted to multiplication and then laws of multiplication applied, A/a = (1/a) A, a≠0 Product is associative with respect to scalar multiplication a(bA) = (ab)A Product is distributive with respect to scalar addition (a + b)A = aA + bA Product is distributive with respect to vector addition a(A + B) = aA + aB Vector addition Parallelogram law SHOW – Join the tails – Draw parallel dashed lines from the head of each vector to the intersection at a common point – Resultant, R, is the diagonal of the parallelogram (extends from the tails of the two vectors to the intersection of the dashed lines) – Special case – two vectors collinear – parallelogram law reduces to an algebraic or scalar addition, R = A + B Triangular construction (head-to-tail fashion) SHOW – Adding B to A – Connect the tail of vector B to the head of vector A – Resultant, R, extends from the tail of vector A to the head of vector B Vector addition is commutative, A + B = B + A Vector addition is associative, (A + B) + D = A + (B + D) Vector subtraction Difference between two vectors A and B – Subtraction defined as a special case of addition – R’ = A – B = A + (-B) = A + (-1)B SHOW Resolution of a vector Vector may be resolved into two “components” having known lines of action by using the parallelogram law – SHOW – Starting at the head of R, extend dashed line parallel to a until it intersects b, likewise dashed line parallel to b until it intersects a – Two components A and B are then drawn such that they extend from the tail of R to the points of intersection – R is resolved into the vector components A and B Problems in Statics involving force (a vector quantity) Find the resultant force, knowing its components Resolve a known force into its components Procedure for analysis – addition of forces Apply parallelogram law – Sketch vector addition using parallelogram law – Determine interior angles from geometry of the problem (recall sum total of interior angles of parallelogram = 360°) – Label known angles and known forces – Redraw half portion of constructed parallelogram to show triangular head-to-tail addition components – Unknowns can be determined from known data on triangle and use of trigonometry – If no 90° angle, law of sines and/or law of cosines may be used SHOW – EXAMPLES (pgs 29-32) Vector components parallel to x and y axes (Cartesian components) F can be resolved into its vector components Fx and Fy parallel to the x and y axes, F = Fx + Fy Unit vectors i and j designate directions along the x and y axes – – SHOW – – – – – i and j vectors have a dimensionless magnitude of unity Their direction will be described analytically by a “+” or “-” depending on whether they are pointing along the positive or negative x or y axis F = Fxi + Fyj (Cartesian vector form) F’ = F’x(-i) + F’y(-j) = - F’x(i) - F’y(j) The magnitude of each component of F is always a positive quantity, represented by the scalars Fx and Fy The magnitude of F is given in terms of its components by the Pythagorean theorem, F Fx2 Fy2 The direction angle θ, which specifies the orientation of the force, is determined from trigonometry, F tan 1 y Fx From this point forward i and j will simply be written in regular type since by definition they are vectors Addition of vectors in terms of their (Cartesian) components F1 = (F1xi + F1yj), F2 = (F2xi + F2yj), F3 = (F3xi + F3yj) FR = F1 + F2 + F3 FR = (F1xi + F1yj) + (F2xi + F2yj) + (F3xi + F3yj) FR = F1xi + F2xi + F3xi + F1yj + F2yj + F3yj FR = (F1x + F2x + F3x) i + (F1y + F2y + F3y) j FR = FRxi + FRyj – FRx = F1x + F2x + F3x or FRx = ∑ Fx – FRy = F1y + F2y + F3y or FRy = ∑ Fy EXAMPLES (pgs 40-43) Rectangular components of a 3-D vector Assume right-handed coordinate system A = Ax + Ay + Az SHOW Cartesian vector notation, A = Axi + Ayj + Azk Magnitude of Cartesian vector – A = (Ax2 + Ay2 + Az2)1/2 – SHOW Direction of Cartesian vector – SHOW – cos α = Ax/A, cos β = Ay/A, cos γ = Az/A Unit vector Unit vector has a magnitude of 1 and specifies a direction If a unit vector uA and a vector A have the same direction → A can be written as the product of its magnitude A and the unit vector uA, A = A uA – uA (dimensionless) defines the direction and sense of A – A (has dimensions) defines the magnitude of A A unit vector having the same direction as A is represented by uA = A/A Using the unit vector to obtain the direction cosines A unit vector in the direction of A (A = Axi + Ayj + Azk) uA = A/A = Ax/A i + Ay/A j + Az/A k uA = A/A = uAxi + uAyj + uAzk (Ax/A = uAx = cos α, Ay/A = uAy = cos β, Az/A = uAz = cos γ) uA = A/A = cos α i + cos β j + cos γ k (uA has a magnitude 1 and recalling that A = (Ax2 + Ay2 + Az2)1/2) 2 2 2 1 = (cos α + cos β + cos γ) 1/2 Squaring both sides 2 2 2 1 = cos α + cos β + cos γ Equation can be used to determine one of the coordinate direction angles if the other two are known Addition and subtraction of 3-D Cartesian vectors A = (Axi + Ayj + AZk), B = (Bxi + Byj + BZk) R = A + B = (Ax + Bx) i + (Ay + By) j + (Az + Bz) k R’ = A - B = (Ax - Bx) i + (Ay - By) j + (Az - Bz) k FR = ∑ F = ∑ Fxi + ∑ Fyj + ∑ Fzk EXAMPLES (pgs 52-55) Position vector If r extends from point A (xA, yA, zA) to point B (xB, yB, zB) – SHOW – rAB = (xB – xA) i + (yB – yA) j + (zB – zA) k The i, j, k components of the position vector rAB may be formed by taking the coordinates at the head of the vector (point B, (xB, yB, zB)) and subtracting the corresponding coordinates of the tail of the vector (point A, (xA, yA, zA)) Force vector directed along a line The direction of a force can be specified by two points through which its line of action passes Formulate F in a Cartesian vector form, realizing it has the same direction as the position vector r directed from point A to point B (A and B are points on a cord along F) F = Fu = F (r/r) Procedure for analysis – Determine position vector r directed from A to B, and compute its magnitude r – Determine the unit vector u = r/r which defines the direction of both r and F – Determine F by combining its magnitude F and direction u F = Fu EXAMPLES (pgs 65-68) Dot product Dot product of vectors A and B, A∙B, “A dot B” – A∙B = AB cos θ (where 0°≤θ≤180°), SHOW – The result is a scalar, not a vector – The dot product is also referred to as the scalar product of vectors Applicable laws of operation – Commutative law: A∙B = B∙A – Multiplication by a scalar: a (A∙B) = (aA)∙B = A∙(aB) = (A∙B) a – Distributive law: A∙(B + D) = (A∙B) + (A∙D) Cartesian vector formulation – – – – i∙i = (1)(1) cos 0° = 1 i∙j = (1)(1) cos 90° = 0 i∙k = (1)(1) cos 90° = 0 Similarly, j∙j = 1, k∙k = 1, j∙k = 0 Dot product of two general vectors A∙B = (Axi + Ayj + AZk)∙(Bxi + Byj + BZk) = AxBx (i∙i) + AxBy (i∙j) + AxBZ (i∙k) + AyBx (j∙i) + AyBy (j∙j) + AyBz (j∙k) + AzBx (k∙i) + AzBy (k∙j) + AzBz (k∙k) = AxBx + AyBy + AzBz Applications of dot product Determining the angle formed between two vectors or intersecting lines (recall A∙B = AB cos θ) θ = cos-1 (A∙B/AB), 0°≤θ≤180° A∙B is computed from A∙B = AxBx + AyBy + AzBz if A∙B = 0 → θ = 90° → A is perpendicular to B Applications of dot product (continued) Components of a vector parallel and perpendicular to a line (aa’) – SHOW – Parallel For Ap (projection of A onto line aa’) → Ap = A cos θ Direction of line specified by the unit vector u (u=1) Ap = A cos θ = (A)(1) cos θ = A∙u [and Ap = (A∙u)(u)] The scalar projection of A along a line is determined from the dot product of A and the unit vector u which defines the direction of the line If Ap is positive, then Ap has a sense which is the same as u If Ap is negative, then Ap has the opposite sense to u – Perpendicular A = Ap + An → An = A - Ap An → An = A sin θ, θ = cos-1 (A∙u/A) Or by Pythagorean Theorem An = (A2 – Ap2)1/2 EXAMPLES (pg 76-80)