* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download AC Circuits and Resonance Conclusion
Survey
Document related concepts
Crystal radio wikipedia , lookup
Standing wave ratio wikipedia , lookup
Operational amplifier wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Power MOSFET wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Flexible electronics wikipedia , lookup
Power electronics wikipedia , lookup
Radio transmitter design wikipedia , lookup
Integrated circuit wikipedia , lookup
Regenerative circuit wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Surge protector wikipedia , lookup
Opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Index of electronics articles wikipedia , lookup
Transcript
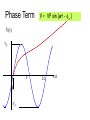
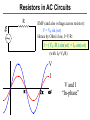
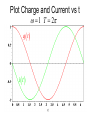
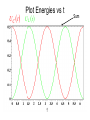
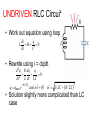
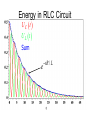
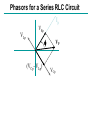
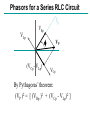
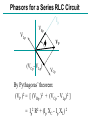
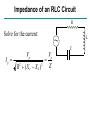
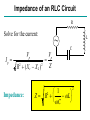
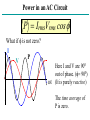
AC Circuits and Resonance Conclusion April 20, 2005 Alternating Current Circuits An “AC” circuit is one in which the driving voltage and hence the current are sinusoidal in time. V(t) Vp fv p 2p wt V = VP sin (wt - fv ) I = IP sin (wt - fI ) -Vp w is the angular frequency (angular speed) [radians per second]. Sometimes instead of w we use the frequency f [cycles per second] Frequency f [cycles per second, or Hertz (Hz)] w = 2p f Phase Term V = VP sin (wt - fv ) V(t) Vp p fv -Vp 2p wt Resistors in AC Circuits R E ~ EMF (and also voltage across resistor): V = VP sin (wt) Hence by Ohm’s law, I=V/R: I = (VP /R) sin(wt) = IP sin(wt) (with IP=VP/R) V I p 2p wt V and I “In-phase” Capacitors in AC Circuits C Start from: q = C V [V=Vpsin(wt)] Take derivative: dq/dt = C dV/dt So I = C dV/dt = C VP w cos (wt) E ~ I = C w VP sin (wt + p/2) V I p 2p wt This looks like IP=VP/R for a resistor (except for the phase change). So we call Xc = 1/(wC) the Capacitive Reactance The reactance is sort of like resistance in that IP=VP/Xc. Also, the current leads the voltage by 90o (phase difference). V and I “out of phase” by 90º. I leads V by 90º. I Leads V??? What the **(&@ does that mean?? 2 V f 1 I I = C w VP sin (wt + p/2) Current reaches it’s maximum at an earlier time than the voltage! Inductors in AC Circuits ~ L V = VP sin (wt) Loop law: V +VL= 0 where VL = -L dI/dt Hence: dI/dt = (VP/L) sin(wt). Integrate: I = - (VP / Lw) cos (wt) or V Again this looks like IP=VP/R for a resistor (except for the phase change). I p I = [VP /(wL)] sin (wt - p/2) 2p wt So we call the XL = w L Inductive Reactance Here the current lags the voltage by 90o. V and I “out of phase” by 90º. I lags V by 90º. Phasor Diagrams A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. The “y component” is the actual voltage or current. Resistor Vp Ip wt Phasor Diagrams A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. The “y component” is the actual voltage or current. Resistor Capacitor Vp Ip Ip wt wt Vp Phasor Diagrams A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. The “y component” is the actual voltage or current. Resistor Capacitor Inductor Vp Ip Vp Ip wt Ip wt wt Vp i i + + + time i i LC Circuit i i + + + Analyzing the L-C Circuit Total energy in the circuit: 1 2 1 q2 U = UB UE = LI 2 2 C 2 Differentiate : dU d 1 2 1 q = ( LI ) = 0 N o change in energy dt dt 2 2 C dI q dq dq d 2 q q dq LI = 0 = L( ) 2 dt C dt dt dt C dt d 2q 1 L 2 q = 0 dt C Analyzing the L-C Circuit Total energy in the circuit: 1 2 1 q2 U = UB UE = LI 2 2 C 2 Differentiate : dU d 1 2 1 q = ( LI ) = 0 N o change in energy dt dt 2 2 C dI q dq dq d 2 q q dq LI = 0 = L( ) 2 dt C dt dt dt C dt d 2q 1 L 2 q = 0 dt C Analyzing the L-C Circuit Total energy in the circuit: 1 2 1 q2 U = UB UE = LI 2 2 C 2 Differentiate : dU d 1 2 1 q = ( LI ) = 0 N o change in energy dt dt 2 2 C dI q dq dq d 2 q q dq LI = 0 = L( ) 2 dt C dt dt dt C dt d 2q 1 L 2 q = 0 dt C Analyzing the L-C Circuit Total energy in the circuit: 1 2 1 q2 U = UB UE = LI 2 2 C 2 Differentiate : d 2q 2 w q=0 2 dt q = q p cos wt dU d 1 2 1 q = ( LI ) = 0 N o change in energy dt dt 2 2 C dI q dq dq d 2 q q dq LI = 0 = L( ) 2 dt C dt dt dt C dt d 2q 1 L 2 q = 0 dt C The charge sloshes back and forth with frequency w = (LC)-1/2 LC Oscillations • Work out equation for LC circuit (loop rule) C q di L =0 C dt • Rewrite using i = dq/dt d 2q q d 2q 2 L 2 =0 w q=0 2 C dt dt – w (angular frequency) has dimensions of 1/t w= 1 LC • Identical to equation of mass on spring m d 2x dt 2 kx = 0 d 2x dt 2 w x = 0 2 k w= m L LC Oscillations (2) • Solution is same as mass on spring oscillations q = qmax cos w t ) i = w qmax sin w t ) = imax sin w t ) – qmax is the maximum charge on capacitor – is an unknown phase (depends on initial conditions) • Calculate current: i = dq/dt Plot Charge and Current vs t w = 1 T = 2p q t ) i t ) Energy Oscillations Equation of LC circuit di q L =0 dt C • Total energy in circuit is conserved. Let’s see why di q dq L i =0 dt C dt ) (Multiply by i = dq/dt) ) Ld 2 1 d 2 i q =0 2 dt 2C dt d 1 2 1 q2 2 Li 2 = 0 dt C dx 2 dx Use = 2x dt dt 2 q 1 Li 2 1 = const 2 2 C UL + UC = const Oscillation of Energies • Energies can be written as (using w2 = 1/LC) 2 q 2 qmax UC = = cos 2 w t ) 2C 2C 2 q 2 U L = 12 Li 2 = 12 Lw 2 qmax sin 2 w t ) = max sin 2 w t ) 2C • Conservation of energy: 2 qmax UC U L = = const 2C • Energy oscillates between capacitor and inductor – Endless oscillation between electrical and magnetic energy – Just like oscillation between potential energy and kinetic energy for mass on spring Plot Energies vs t UC t ) U L t ) Sum UNDRIVEN RLC Circuit • Work out equation using loop rule di q L Ri = 0 dt C • Rewrite using i = dq/dt d 2q R dq q =0 2 L dt LC dt 2 tR / 2 L q = qmax e cos w t ) w = 1/ LC R / 2 L ) • Solution slightly more complicated than LC case Charge and Current vs t in RLC Circuit q t ) i t ) e tR / 2 L RLC Circuit (Energy) di q L Ri = 0 dt C Basic RLC equation di q dq 2 L i Ri =0 dt C dt Multiply by i = dq/dt d 1 2 1 q2 2 Li = i R 2 2 dt C Collect terms (similar to LC circuit) d U L U C ) = i 2 R dt Total energy in circuit decreases at rate of i2R (dissipation of energy) U tot etR / L Energy in RLC Circuit UC t ) U L t ) Sum e tR / L AC Circuits • Enormous impact of AC circuits – – – – – Power delivery Radio transmitters and receivers Tuners Filters Transformers • Basic components – – – – R L C Driving emf AC Circuits and Forced Oscillations • RLC + “driving” EMF with angular frequency wd = m sin wd t L di q Ri = m sin w d t dt C • General solution for current is sum of two terms “Transient”: Falls exponentially & disappears Ignore i etR / 2 L cos w t “Steady state”: Constant amplitude Steady State Solution • Assume steady state solution of form i = I m sin w d t f ) – Im is current amplitude – f is phase by which current “lags” the driving EMF – Must determine Im and f • Plug in solution: differentiate & integrate sin(wt-f) i = I m sin w d t f ) di = w d I m cos w d t f ) dt Im q= cos w d t f ) Substitute di q L Ri = m sin w t dt C wd Im I mw d L cos w d f ) I m R sin w d t f ) cos w d t f ) = m sin w d t wd C Steady State Solution for AC Im Current (2) I mw d L cos w d f ) I m R sin w d t f ) cos w d t f ) = m sin w d t wd C • Expand sin & cos expressions sin wd t f ) = sin wd t cos f cos w d t sin f cos wd t f ) = cos wd t cos f sin w d t sin f High school trig! • Collect sinwdt & coswdt terms separately coswdt terms wd L 1/ wd C ) cos f R sin f = 0 sinwdt terms I m wd L 1/ wd C ) sin f I m R cos f = m • These equations can be solved for Im and f (next slide) Steady State Solution for AC Current (3) wd L 1/ wd C ) cos f R sin f = 0 I m wd L 1/ wd C ) sin f I m R cos f = m • Solve for f and Im in terms of tan f = wd L 1/ wd C R X XC L R Im = m Z • R, XL, XC and Z have dimensions of resistance X L = wd L Inductive “reactance” X C = 1/ wd C Capacitive “reactance” Z = R2 X L X C ) 2 Total “impedance” • Let’s try to understand this solution using “phasors” REMEMBER Phasor Diagrams? A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. Resistor Capacitor Inductor Vp Ip Vp Ip wt Ip wt wt Vp Reactance - Phasor Diagrams Resistor Capacitor Inductor Vp Ip Vp Ip wt Ip wt wt Vp “Impedance” of an AC Circuit R L ~ C The impedance, Z, of a circuit relates peak current to peak voltage: Ip = Vp Z (Units: OHMS) “Impedance” of an AC Circuit R L ~ C The impedance, Z, of a circuit relates peak current to peak voltage: Ip = Vp Z (Units: OHMS) (This is the AC equivalent of Ohm’s law.) Impedance of an RLC Circuit R E ~ L C As in DC circuits, we can use the loop method: E - V R - VC - VL = 0 I is same through all components. Impedance of an RLC Circuit R E ~ L C As in DC circuits, we can use the loop method: E - V R - VC - VL = 0 I is same through all components. BUT: Voltages have different PHASES they add as PHASORS. Phasors for a Series RLC Circuit Ip VLp VRp f (VCp- VLp) VP VCp Phasors for a Series RLC Circuit Ip VLp VRp f (VCp- VLp) VP VCp By Pythagoras’ theorem: (VP )2 = [ (VRp )2 + (VCp - VLp)2 ] Phasors for a Series RLC Circuit Ip VLp VRp f (VCp- VLp) VP VCp By Pythagoras’ theorem: (VP )2 = [ (VRp )2 + (VCp - VLp)2 ] = Ip2 R2 + (Ip XC - Ip XL) 2 Impedance of an RLC Circuit R Solve for the current: Ip = Vp Vp = Z R2 (X c X L )2 ~ L C Impedance of an RLC Circuit R Solve for the current: Ip = ~ L C Vp = Z R2 (X c X L )2 Impedance: Vp Z= 1 R wL wC 2 2 Impedance of an RLC Circuit Vp Ip = Z 1 R wL wC Z= The current’s magnitude depends on the driving frequency. When Z is a minimum, the current is a maximum. This happens at a resonance frequency: 2 2 The circuit hits resonance when 1/wC-wL=0: w r=1/ LC When this happens the capacitor and inductor cancel each other and the circuit behaves purely resistively: IP=VP/R. IP R =10W L=1mH C=10mF R = 1 0 0 W 0 1 0 wr 2 1 0 3 1 0 4 1 0 5 w The current dies away at both low and high frequencies. Phase in an RLC Circuit Ip VLp We can also find the phase: VRp (VCp- VLp) f VP tan f = (VCp - VLp)/ VRp or; or VCp tan f = (XC-XL)/R. tan f = (1/wC - wL) / R Phase in an RLC Circuit Ip VLp We can also find the phase: VRp (VCp- VLp) f VP tan f = (VCp - VLp)/ VRp or; or VCp tan f = (XC-XL)/R. tan f = (1/wC - wL) / R More generally, in terms of impedance: cos f = R/Z At resonance the phase goes to zero (when the circuit becomes purely resistive, the current and voltage are in phase). Power in an AC Circuit V f= 0 p I 2p wt V(t) = VP sin (wt) I(t) = IP sin (wt) (This is for a purely resistive circuit.) P P(t) = IV = IP VP sin 2(wt) Note this oscillates twice as fast. p 2p wt Power in an AC Circuit The power is P=IV. Since both I and V vary in time, so does the power: P is a function of time. Use, V = VP sin (wt) and I = IP sin (w t+f ) : P(t) = IpVpsin(wt) sin (w t+f ) This wiggles in time, usually very fast. What we usually care about is the time average of this: 1 T P = 0 P( t )dt T (T=1/f ) Power in an AC Circuit Now: sin( wt f ) = sin( wt )cos f cos(wt )sin f Power in an AC Circuit Now: sin( wt f ) = sin( wt )cos f cos(wt )sin f P( t ) = I PVP sin( w t )sin( w t f ) = I PVP sin 2( w t )cos f sin( w t )cos( w t )sin f Power in an AC Circuit Now: sin( wt f ) = sin( wt )cos f cos(wt )sin f P( t ) = I PVP sin( w t )sin( w t f ) = I PVP sin 2( w t )cos f sin( w t )cos( w t )sin f Use: and: So sin (w t ) = 2 1 2 sin(w t ) cos(w t ) = 0 P = 1 2 I PV P cos f Power in an AC Circuit Now: sin( wt f ) = sin( wt )cos f cos(wt )sin f P( t ) = I PVP sin( w t )sin( w t f ) = I PVP sin 2( w t )cos f sin( w t )cos( w t )sin f Use: and: So sin (w t ) = 2 1 2 sin(w t ) cos(w t ) = 0 P = 1 2 I PV P cos f which we usually write as P = IrmsVrms cos f Power in an AC Circuit P = IrmsVrms cos f f goes from -900 to 900, so the average power is positive) cos(f) is called the power factor. For a purely resistive circuit the power factor is 1. When R=0, cos(f)=0 (energy is traded but not dissipated). Usually the power factor depends on frequency. Power in an AC Circuit P = IrmsVrms cos f What if f is not zero? I P V Here I and V are 900 out of phase. (f= 900) wt (It is purely reactive) The time average of P is zero. STOP! Transformers Transformers use mutual inductance to change voltages: N2 V2 = V1 N1 N1 turns Iron Core V1 Primary Power is conserved, though: (if 100% efficient.) N2 turns V2 Secondary I1V1 = I 2V2 Transformers & Power Transmission Transformers can be used to “step up” and “step down” voltages for power transmission. 110 turns Power =I1 V1 V1=110V 20,000 turns V2=20kV Power =I2 V2 We use high voltage (e.g. 365 kV) to transmit electrical power over long distances. Why do we want to do this? Transformers & Power Transmission Transformers can be used to “step up” and “step down” voltages, for power transmission and other applications. 110 turns Power =I1 V1 V1=110V 20,000 turns V2=20kV Power =I2 V2 We use high voltage (e.g. 365 kV) to transmit electrical power over long distances. Why do we want to do this? P = I2R (P = power dissipation in the line - I is smaller at high voltages)