Download Unit 2 - Mona Shores Blogs

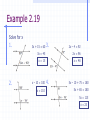
Unit 2
Basic Geometric Elements
Lesson 2.1
Points, Lines, and Planes
Lesson 2.1 Objectives
Define and write notation of the following:











Point
Line
Plane
Ray
Line segment
Collinear
Coplanar
End point
Initial point
Opposite rays
Intersection
(G1.1.6)
Start-Up
Give your definition
of the following:


Point
Line
These terms are
actually said to be
undefined, or have
no formal definition.
However, it is
important to have a
general agreement
on what each word
means.
Point
A point has no dimension, it is merely
a location.

Meaning it takes up no space.
It is usually represented as a dot.
When labeling we designate a capital
letter as a name for that point.

We may call it Point A.
A
Line
A line extends in one dimension.

Meaning it goes straight in either a vertical, horizontal, or
slanted fashion.
It extends forever in two directions.
It is represented by a line with an arrow on each
end.
When labeling, we use lower-case letters to name the
line.


Or the line can be named using two points that are on the
line.
So we say Line n, or AB
n
A
B
A
Plane
M
C
B
A plane extends in two dimensions.

Meaning it stretches in a vertical direction as well as a
horizontal direction at the same time.
It also extends forever.
It is usually represented by a shape like a tabletop or
a wall.
When labeling we use a bold face capital letter to
name the plane.


Plane M
Or the plane can be named by picking three points in the
plane and saying Plane ABC.
Collinear
The prefix co- means the same, or to
share.
Linear means line.
 So collinear means that points lie on
the same line.
A
B
C
We say that points A, B, and C are collinear.
Coplanar
Coplanar points are points that lie on
the same plane.
A
M
C
B
So points A, B, and C are said to be coplanar.
Line Segment
Consider the line AB.

It can be broken into smaller pieces by
merely chopping the arrows off.
This creates a line segment or
segment that consists of endpoints A
and B.

This is symbolized as AB
B
A
Ray
A ray consists of an initial point where
the figure begins and then continues in
one direction forever.

It looks like an arrow.
This is symbolized by writing its initial
point first and then naming any other
point on the ray, AB .

Or we can say ray AB.
B
A
Betweenness
When three points lie on a line, we can
say that one of them is between the
other two.


A
This is only true if all three points are
collinear.
We would say that B is between A and C.
B
C
Opposite Rays
If C is between A and B on a line, then
ray CA and ray CB are opposite rays.

Opposite rays are only opposite if they are
collinear.
A
C
B
Intersections of
Lines and Planes
Two or more geometric figures intersect if they
have one or more points in common.


If there is no point or points shown, they the figures do not
intersect.
The intersection of the figures is the set of points the
figures have in common.
Two lines intersect at one point.
Two planes intersect at one line.
A
m
n
Example 2.1
4.
Plane DEF
D
Draw the following
1.
AB
5.
B
DE intersected by FG at po int H .
G
H
F
CD
D
C
E
D
A
2.
F
E
6. If M is between N and L,
draw the opposite rays MN and ML.
3.
EF
E
F
N
M
L
Example 2.2
Answer the following
1. Name 3 points that are collinear.
1.
2.
C, B, D
Name 3 points that are not collinear.
2.
3.
ex: A, B, E or A, B, C
Name 3 points that are coplanar.
3.
4.
ex: A, B, E or B, C, D or B, C, E
Name 4 points that are not coplanar.
4.
5.
ex: A, B, E, C
What are two ways to name the plane?
5.
6.
Plane ABE or Plane F
What are two names for the line that passes through points C
and B.
6.
line g or BC
Homework 2.1
Lesson 2.1 – Point, Line, Plane

p1-2
Due Tomorrow
Lesson 2.2
Distance,
Midpoint, and
Segment Addition
Lesson 2.2 Objectives
Utilize the distance formula. (G1.1.3)
Apply the midpoint formula. (G1.1.5)
Justify the construction of a midpoint. (G1.1.5)
Utilize the segment addition postulate. (G1.1.3)
Identify the symbol and definition of
congruent. (G1.1.3)
Define segment bisector. (G1.1.3)
Postulate 1: Ruler Postulate
The points on a line can be matched to
real numbers called coordinates.
The distance between the points, say
A and B, is the absolute value of the
difference of the coordinates.

Distance is always positive.
E
C
A
B D
Length
Finding the distance between points A
and B is written as

AB
Writing AB is also called the length of
line segment AB.
Postulate 2: Segment Addition Postulate
If B is between A and C, then

AB + BC = AC.
Also, the opposite is true.

If AB + BC = AC, then B is between A and
C.
BC
AB
A
B
C
AC
Example 2.3
1. Sketch and write the segment addition postulate if
point E is between points D and F.
D
E
F
DE + EF = DF
2. Sketch and write the segment addition postulate if
point M is between points N and P.
N
M
P
NM + MP = NP
Example 2.4
Find
1.
GJ
GJ = 16
1.
2.
KM
KM = 36
2.
3.
XY
71-29
XY = 42
3.
4.
LM
4.
x + 2x = 18
3x = 18
x=6
LM = 6
Distance Formula
To find the distance on a graph between two
points
A(1,2)
AB =
B(7,10)
We use the Distance Formula
(x2 – x1)2 + (y2 – y1)2
Distance can also be found using the Segment Addition
Postulate, which simply adds up each segment of a line
to find the total length of the line.
Congruent Segments
Segments that have the same length
are called congruent segments.

This is symbolized by
.
Hint: If the symbols are there, the
congruent sign should be there.
LE  NT
If you want to state
two segments are
congruent, then you
write
LE  NT
If you want to state
two lengths are equal,
then you write
Example 2.5
(x2 – x1)2 + (y2 – y1)2
Find the distance of each segment and identify if any of the
segments are congruent.
3. A(4,3)
1. J(1,1)
2
2
2
2
(

1

4)

(6

3)
(0

1)

(5

1)
B(-1,6)
K(0,5)
(5) 2  (3) 2
(1)2  (4) 2
JK  LM
2.
L(2,1)
M(-2,0)
25  9
34  5.83
1  16
17  4.12
(2  2) 2  (0  1) 2
(4) 2  ( 1) 2
16  1
17  4.12
4.
D(2,-3)
E(-2,0)
(2  2) 2  (0  3) 2
(4)2  (3)2
16  9
25  5
Midpoint
The midpoint of a segment is the point that
divides the segment into two congruent
segments.

J
The midpoint bisects the segment, because
bisect means to divide into two equal parts.
O
We say that O is the midpoint
of line segment JY.
Y
Midpoint Formula
We can also find the midpoint of segment AB by
using its endpoints in…
The Midpoint Formula
A(1,2) B(7,10)
Midpoint of AB =
(
(y1 + y2)
(x1 + x2)
2
,
2
)
This gives the coordinates of the midpoint, or point that
is halfway between A and B.
Example 2.6
Find the midpoint
1. R(3,1)
S(3,7)
(
(y1 + y2)
(x1 + x2)
,
2
2.
2
T(2,4)
S(6,6)
 3  3 1 7 
,


2 
 2
6 8
 , 
2 2
 26 46
,


2 
 2
 8 10 
 , 
2 2 
3, 4
 4,5
)
Finding the Other End
M
Many may say finding the
midpoint is easy!

It is simply the average of the
two endpoints.
Now imagine knowing the
midpoint, one endpoint, and
trying to find the coordinates of
the other endpoint.


Try to remember what the
midpoint formula does and work
it backwards.
So here is what we are going to
do:
1.
2.
Double the coordinates of the
midpoint.
Subtract the coordinates of the
known endpoint.
F (7,13)
?
E
M (5, 7)
2
E (3,1)
(10,14)
 (3,1)
(7,13)
Example 2.7
Find the other endpoint given one endpoint, E,
and the midpoint, M.
1.
E(0,5)
2.
M(3,3)
(3,3)  2
(6, 6)
 (0,5)
(6,1)
E(-1,-3)
M(5,9)
(5,9)  2
(10,18)
 (1, 3)
(11, 21)
Segment Bisector
A segment bisector is a segment, ray, line,
or plane that intersects the original segment
at its midpoint.
T
J
O
H
So HT is a segment bisector of JY .
Y
Example 2.8
Use the diagram to find the given
measure if line l is a segment bisector.
109 in
ST = ½(109 in)
ST = 54.5 in
Homework 2.2
Lesson 2.2 – Line Segments

p3-4
Due Tomorrow
Lesson 2.3
Angles and Their Measures
Lesson 2.3 Objectives
Identify more than one name for an angle.
(G1.1.6)
Identify angle measures. (G1.1.6)
Classify angles as right, obtuse, acute, or
straight. (G1.1.6)
Apply the angle addition postulate. (G1.1.3)
Utilize angle vocabulary to solve problems.
(G1.1.6)
Define angle bisector and its uses.
(G1.1.3)
What is an Angle?
An angle consists of two different rays
that have the same initial point.
The rays form the sides of the angle.
The initial point is called the vertex of
the angle.

Vertex can often be thought of as a corner.
Naming an Angle
All angles are named by using three points


First, name a point that lies on one side of the angle.
Second, name the vertex next.
 The vertex is always named in the middle.

Finally, name a point that lies on the opposite side of the
angle.
So we can call It
Or NOW
O
WON
W
N
Using a Protractor
1.
2.
3.
To measure an angle with a protractor, do the following:
Place the cross-hairs of the protractor on the vertex of the angle.
Line up one side of the angle with the 0o line near the bottom of the
protractor.
Read the protractor for the where the other side of the angle points.
54o
Example 2.9
Protractor Stations
Congruent Angles
Congruent angles are angles that have the
same measure.

To show that we are finding the measure of an
angle…
 Place a “m” before the name of the angle.
mWON  mNOW
WON  NOW
Equal Measures
Congruent Angles
Types of Angles
Acute
Right
Obtuse
Straight
Less than 90
(<90)
Equal to 90
(=90)
Greater than 90
(>90)
Equal to 180
(=180)
Looks like
Measure
Example 2.10
Give another name for the angle in the diagram above. Then, tell whether
the angle appears to be acute, obtuse, right, or straight.
1.
JKN
 NKJ,  K
1.
1.
2.
KMN
2.
 NMK
2.
3.
 MQP
3.
acute
JML
4.
 LMJ
4.
5.
straight
PQM
3.
4.
right
acute
PLK
5.
 KLP
5.
obtuse
Other Parts of an Angle
The interior of an angle is defined as the set
of points that lie between the sides of the
angle.
The exterior of an angle is the set of points
that lie outside of the sides of the angle.
Exterior
Interior
Postulate 4: Angle Addition Postulate
The Angle Addition Postulate allows
us to add each smaller angle together
to find the measure of a larger angle.
What is the
total?
49o
32o
17o
Example 2.11
Use the given information to find the indicated
measure.
3x + 15 + x + 7 = 94
1.
4x + 22 = 94
4x = 72
25o
2.
x = 18
3x + 1 + 2x – 6 = 135
3(28) + 1
84 + 1
85
85o
5x – 5 = 135
5x = 140
x = 28
Adjacent Angles
Two angles are adjacent angles if
they share a common vertex and side,
but have no common interior points.

Basically they should be touching, but not
overlapping.
C
CAT and TAR
are adjacent.
CAR and TAR
are not adjacent.
T
A
R
Angle Bisector
An angle bisector is a ray that divides
an angle into two adjacent angles that
are congruent.

To show that angles are congruent, we use
congruence arcs.
Example 2.12
In the diagram, BD bisects ABC. Find mABC.
2.
1.
4x = 3x + 6
x=6
3.
5x – 11 = 4x + 1
x – 11 = 1
x = 12
8x – 16 = 4x + 20
4x – 16 = 20
4x = 36
x=9
4(6) + 3(6) + 6
24 + 18 + 6
mABC = 48o
5(12) – 11 + 4(12) + 1
60 – 11 + 48 + 1
mABC = 98o
2(4(9) + 20)
2(56)
mABC = 112o
Homework 2.3
Lesson 2.3 - Angles and Their Measures

p5-7
Due Tomorrow
Lesson 2.4
Angle Pair Relationships
Lesson 2.4 Objectives
Identify vertical angle pairs. (G1.1.1)
Identify linear pairs. (G1.1.1)
Differentiate between complementary and
supplementary angles. (G1.1.1)
Vertical Angles
Two angles are vertical angles if their sides form
two pairs of opposite rays.

Basically the two lines that form the angles are straight.
To identify the vertical angles, simply look straight
across the intersection to find the angle pair.

Hint: The angle pairs do not have to be vertical in position.
Vertical Angle pairs are always congruent!
4
1
3
2
4
1
3
2
Linear Pair
Two adjacent angles form a linear pair if their noncommon sides are opposite rays.

Simply put, these are two angles that share a straight line.
 Just like neighbors share a fence line, but they must live on
the same side of the road.
Since they share a straight line, their sum is…

180o
1
2
Example 2.13
Find the measure of all unknown angles, when m1 = 57o.
1.
m2
1.
2.
123o
m3
2.
3.
57o
m4
3.
123o
16y - 27 = 13y
Example 2.14
-27 = -3y
y=9
Solve for x and y.
1.
2.
3x + 48 = 180
3x = 132
x = 44
3.
9x + 7 = 5x + 67
7x = 5x + 18
4x + 7 = 67
2x = 18
4x = 60
x = 15
x=9
Complementary v Supplementary
Complementary
angles are two
angles whose sum is
90o.

Complementary
angles can be
adjacent or nonadjacent.
Supplementary
angles are two
angles whose sum is
180o.

Supplementary
angles can be
adjacent or nonadjacent.
Example 2.15
Find the measure of all unknown angles, given that m and n form a right
angle and the m1 = 22o and 1  4.
1.
m2
1.
68o
2.
m5
m
2.
22o
3.
m6
3.
68o
4.
m4
n
o
4.
22
5.
m3
5.
68o
6.
m7
6.
68o
7.
m8
7.
22o
Example 2.16
A and B are complementary.
Find mA and mB.
1.
mA = 2x + 12
mB = 9x – 10
1.
2x + 12 + 9x – 10 = 90
11x + 2 = 90
11x = 88
x=8
A and B are supplementary.
Find mA and mB.
2.
mA = 12x + 32
mB = 4x – 12
2.
12x + 32 + 4x – 12 = 180
16x + 20 = 180
16x = 160
x = 10
mA = 2(8) + 12
mB = 9(8) - 10
mA = 12(10) + 32 mB = 4(10) - 12
mA = 16 + 12
mB = 72 - 10
mA = 120 + 32
mB = 40 - 12
mA = 28o
mB = 62o
mA = 152o
mB = 28o
Perpendicular Lines
When two lines intersect to form a right
angle, they are said to be
perpendicular lines.
So we can say that a  b.
a
b
Homework 2.4
Lesson 2.4 - Angle Pair Relationships

p7-8
Due Tomorrow
Lesson 2.5
Introduction to Parallel Lines
and
Transversals
Lesson 2.5 Objectives
Identify angle pairs formed by a transversal.
(G1.1.2)
Compare parallel and skew lines.
(G1.1.2)
Lines and Angle Pairs
Alternate Exterior Angles –
because they lie outside the
two lines and on opposite sides
Transversal
1 2
4 3
5 6
8 7
Corresponding
Angles –
because they lie
in corresponding
positions of each
intersection.
of the transversal.
Alternate Interior Angles –
because they lie inside the two lines
and on opposite sides of the
transversal.
Consecutive
Interior
Angles –
because they
lie inside the
two lines and
on the same
side of the
transversal.
Example 2.17
Determine the relationship between the given angles
1
3 and 9
1)
2
13 and 5
2)
3
Alternate Interior Angles
5 and 15
4)
5
Corresponding Angles
4 and 10
3)
4
Alternate Interior Angles
Alternate Exterior Angles
7 and 14
5)
Consecutive Interior Angles
Postulate 15:
Corresponding Angles Postulate
If two parallel lines are cut by a transversal, then
corresponding angles are congruent.

You must know the lines are parallel in order to assume the
angles are congruent.
1 2
4 3
5 6
8 7
Theorem 3.4:
Alternate Interior Angles
If two parallel lines are cut by a transversal, then alternate
interior angles are congruent.



Again, you must know that the lines are parallel.
If you know the two lines are parallel, then identify where the
alternate interior angles are.
Once you identify them, they should look congruent and they are.
1 2
4 3
5 6
8 7
Theorem 3.5:
Consecutive Interior Angles
If two parallel lines are cut by a transversal, then
consecutive interior angles are supplementary.


Again be sure that the lines are parallel.
They don’t look to be congruent, so they MUST be
supplementary.
1 2
4 3
180o = +
+
= 180o
5 6
8 7
Theorem 3.6:
Alternate Exterior Angles
If two parallel lines are cut by a transversal, then
alternate exterior angles are congruent.

Again be sure that the lines are parallel.
1 2
4 3
5
6
8 7
Example 2.18
Find the missing angles for the following:
120o
60o
120o
120o
140o
140o
105o
110o
70o
105o
110o
Example 2.19
Solve for x
1.
2.
3x + 15 = 60
3.
2x – 4 = 92
3x = 45
2x = 96
x = 15
x = 48
x – 10 = 100
x = 110
4.
5x – 10 + 75 = 180
5x + 65 = 180
5x = 115
x = 23
Parallel versus Skew
Two lines are parallel if they are coplanar
and do not intersect.
 The short-hand symbol for being parallel is //.
Lines that are not coplanar and do not
intersect are called skew lines.

These are lines that look like they intersect but do
not lie on the same piece of paper.
Skew lines go in different directions while
parallel lines go in the same direction.
Example 2.20
Complete the following statements using the words parallel, skew, perpendicular.
1)
Line WZ and line XY are _________.
1)
2)
Line WZ and line QW are ________.
2)
3)
perpendicular
Line TS and line ZY are __________.
6)
7)
parallel
Plane RQT and plane WQR are _________.
5)
6)
skew
Plane WQR and plane SYT are _________.
4)
5)
perpendicular
Line SY and line WX are _________.
3)
4)
parallel
skew
Line WX and plane SYZ are __________.
7)
parallel.
Homework 2.5
Lesson 2.5

p11-12
Due Tomorrow
Unit 2 Test

Monday, October 11th