Download Given - rreidymath

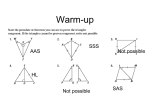
OTCQ
What is the measure of
one angle in a
equilateral/equiangular
triangle?
Aim 4-3 How do we prove theorems
about angles (part 1)?
GG 30, GG 32, GG 34
Objectives
SWBAT to construct the form of a proof and
SWBAT to conjecture about appropriate
statements.
Starters:
Theorem 4-1: If 2 angles are right angles, then
they are congruent.
Theorem 4-1: If 2 angles are straight angles,
then they are congruent.
How could we justify these statements in a
proof?
Prove Theorem 4-2 If two angles are straight
angles, then they are congruent.
A
Given ABC is a straight angle and
DEF is a straight angle.
D
Prove ABC  DEF.
Statements
Reasons
B
C
E
F
4-3 #17.Prove Theorem 4-2 If two angles are
straight angles, then they are congruent.
Given ABC is a straight angle and DEF is a
Straight angle. Prove ABC  DEF.
A
D
Statements
1. ABC is a straight angle and
DEF is a straight angle.
2. m ABC = 180○
3. m DEF = 180○.
Conclusion ABC  DEF.
B
C
E
F
Reasons
1. Given
2. Definition of straight
angle.
3.Definition of straight
angle.
4.Definition of
congruent. QED
Complementary angles are two angles the
○
sum of whose degree measures is 90 .
Supplementary angles are two angles the
sum of whose degree measures is 180○.
Theorem 4-3: If 2 angles are complements
of the same angle then they are
congruent.
Why?
Theorem 4-3: If 2 angles are complements of the
same angle then they are congruent.
Why?
Given
m 1= 45○
m 2= 45○
m 3= 45○
3
1
2
Theorem 4-3: If 2 angles are complements of the
same angle then they are congruent.
Why?
Given
m 1= 45○
m 2= 45○
m 3= 45○
3
1
2
m1+ m 2= 90○ , hence  2 is the complement of  1.
m1+ m 3= 90○ , hence  3 is the complement of  1.
Since 2 and 3 are each the complement of  1,
then 2 and 3 must be congruent.
Theorem 4-4: If 2 angles are congruent then
their complements are congruent.
Why?
Theorem 4-4: If 2 angles are congruent then
their complements are congruent.
Why?
Given
m 1= 30○
m 2= 30○
3
1
4
2
Theorem 4-4: If 2 angles are congruent then their
complements are congruent.
Why?
Given
m 1= 30○
4
3
○
m 2= 30
1
2
If  3 is complementary to 1, what is the degree
measure of 3?
If  4 is complementary to 2, what is the degree
measure of 4?
Theorem 4-4: If 2 angles are congruent then their
complements are congruent.
Why?
Given
m 1= 30○
4
3
○
m 2= 30
1
2
If  3 is complementary to 1, what is the degree
measure of 3? (90○ - 30○ = 60○)
If  4 is complementary to 2, what is the degree
measure of 4?
Theorem 4-4: If 2 angles are congruent then their
complements are congruent.
Why?
34
Given
m 1= 30○
4
3
○
m 2= 30
1
2
If  3 is complementary to 1, what is the degree
measure of 3? (90○ - 30○ = 60○)
If  4 is complementary to 2, what is the degree
measure of 4? (90○ - 30○ = 60○)
Theorem 4-5: If 2 angles are supplements of
the same angle then they are congruent.
Why?
Please try to draw 2 angles that are
supplementary to the same angle.
Theorem 4-5: If 2
angles are
supplements of the
same angle then
they are congruent.
Given: ABC is a
straight angle, we
can say that ABE
is a supplement to
EBC.
E
A
B
D
C
Theorem 4-5: If 2
angles are
supplements of the
same angle then
they are congruent.
Given: ABC is a
straight angle, we
can say that ABE
is a supplement to
EBC.
E
A
B
D
C
Next, given that DBE is a straight angle, we can
say that DBC is a supplement to EBC.
Conclusion: ABE  DBC
Theorem 4-5: If 2
angles are
supplements of the
E
A
same angle then
they are congruent.
Given: ABC is a
B
straight angle, we
can say that ABE
is a supplement to
EBC.
D
C
Next, given that DBE is a straight angle, we can
say that DBC is a supplement to EBC.
Conclusion: ABE  DBC
Theorem 4-5: If 2
angles are
supplements of the
E
A
same angle then
○
65
they are congruent.
Given: ABC is a
○
115
B
straight angle, we
can say that ABE
is a supplement to
○
65
EBC.
D
C
Next, given that DBE is a straight angle, we can
say that DBC is a supplement to EBC.
Theorem 4-6: If 2 angles are congruent then
their supplements are congruent.
Why?
Theorem 4-6: If 2 angles
are congruent then their
supplements are
congruent.
Given:
ABC is a straight angle.
DBE is a straight angle.
ABE  DBC
Conclusion:
ABD  EBC
E
A
65
○
115
B
65
D
○
○
C
Theorem 4-6: If 2 angles
are congruent then their
supplements are
congruent.
Given:
ABC is a straight angle.
DBE is a straight angle.
ABE  DBC
Conclusion:
ABD  EBC
E
A
65
○
115
○
115
B
65
D
○
○
C
Linear pair of angles:
2 adjacent angles whose
sum is a straight angle.
E
A
ABE and EBC are a
linear pair of angles.
65
○
115
○
115
B
The others?
65
D
○
○
C
Linear pair of angles:
2 adjacent angles whose
sum is a straight angle.
Why 4 pairs
of linear pairs?
E
A
ABE and EBC are a
linear pair of angles.
The others?
EBC and CBD.
CBD and DBA.
DBA and ABE.
There should always be
4 pairs of linear pairs
when 2 lines intersect.
65
○
115
○
115
B
65
D
○
○
C
Linear pair of angles:
2 adjacent angles whose
sum is a straight angle.
Theorem 4-7: Linear pairs of
angles are supplementary.
E
A
ABE and EBC are a
linear pair of angles.
The others?
EBC and CBD.
CBD and DBA.
DBA and ABE.
There should always be
4 pairs of linear pairs
when 2 lines intersect.
65
○
115
○
115
B
65
D
○
○
C
Theorem 4-8: If 2 lines intersect to form congruent adjacent
angles, then they are perpendicular.
1
2
4
3
Theorem 4-8: If 2 lines intersect to form congruent adjacent
angles, then they are perpendicular.
Since m1 + m 2 =180○ and  1   2, we may
substitute to say
m 1 + m 1 =180○ and then
2 m 1 =180○ and then
2 m 1 =180○ and then
2
2
m 1 =90○
We can do the same for
 2,  3 and  4
1
2
4
3
Vertical angles:
2 angles in which the sides of
one angle are opposite rays to
the sides of the second angle.
Theorem 4-9.
If two lines intersect, then the
vertical angles are congruent.
Vertical angles:
EBC and ABD.
ABE and DBC.
There should always be 2
pairs of vertical angles pairs
when 2 lines intersect.
E
A
65
○
115
○
115
B
65
D
○
○
C