Download W A T K I N S - J O H N S O N C O M P A N Y Semiconductor

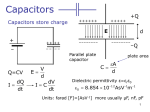
Engineering 43
Capacitors &
Inductors
Bruce Mayer, PE
Licensed Electrical & Mechanical Engineer
[email protected]
Engineering-43: Engineering Circuit Analysis
1
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitance & Inductance
 Introduce Two Energy STORING Devices
• Capacitors
• Inductors
 Outline
• Capacitors
– Store energy in their ELECTRIC field (electroStatic energy)
– Model as circuit element
• Inductors
– Store energy in their MAGNETIC field (electroMagnetic energy)
– Model as circuit element
• Capacitor And Inductor Combinations
– Series/Parallel Combinations Of Elements
Engineering-43: Engineering Circuit Analysis
2
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
The Capacitor
 First of the EnergyStorage Devices
 Basic Physical Model
 Circuit Representation
• Note use of the PASSIVE
SIGN Convention
 Details of Physical
Operation Described in
PHYS4B & ENGR45
Engineering-43: Engineering Circuit Analysis
3
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitance Defined
 Consider the Basic
Physical Model
 Where
• A The Horizontal
Plate-Area, m2
• d  The Vertical Plate
Separation Distance, m
• 0  “Permittivity” of Free
Space; i.e., a vacuum
– A Physical CONSTANT
– Value = 8.85x10-12
Farad/m
 The Capacitance, C,
of the Parallel-Plate
0 A
Structure
C
w/o Dielectric
d
Engineering-43: Engineering Circuit Analysis
4
 Then What are the
UNITS of Capacitance, C
 Typical Cap Values →
“micro” or “nano”
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Circuit Operation
 Recall the Circuit
Representation
 LINEAR Caps Follow the
Capacitance Law; in DC
Q  CVc
 Where
 The Basic CircuitCapacitance Equation
qt   Cvc t 
Engineering-43: Engineering Circuit Analysis
5
• Q  The CHARGE
STORED in the Cap,
Coulombs
• C  Capacitance, Farad
• Vc  DC-Voltage Across
the Capacitor
 Discern the Base Units
for Capacitance
Coulomb
Farad 
Volt Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
“Feel” for Capacitance
 Pick a Cap, Say 12 µF
 Recall Capacitor Law
Q  CVc
 Solving for Vc
Q
15x10 3 Coul
Vc  
C 12x10 6 Coul/Volt
Vc  1250 V!!!
 Now Assume That The
Cap is Charged to hold
15 mC
• Find V c
Engineering-43: Engineering Circuit Analysis
6
 Caps can RETAIN
Charge for a Long Time
after Removing the
Charging Voltage
• Caps can Be
DANGEROUS!
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Forms of the Capacitor Law
 The time-Invariant
Cap Law
Q  CVc
t
vC t 

vC    
 i y dy  C 
dz
 If vC at − = 0, then the
traditional statement of
 Leads to DIFFERENTIAL
the Integral Law
Cap Law
dvC t 
dqt 
i t  
C
dt
dt
1 t
vC t    i y dy
C 
 The Differential Suggests  If at t0, vC = vC(t0) (a
SEPARATING Variables
KNOWN value), then the
Integral Law becomes
i t dt  CdvC t
1 t0
1 t
vC t    i  y dy   i y dy
 Leads to The
C 
C t0
INTEGRAL form of the
1 t
vC t   vC t0    i y dy
Capacitance Law
C t0
Bruce Mayer, PE


Engineering-43: Engineering Circuit Analysis
7
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Integral Law
 Express the VOLTAGE
Across the Cap Using
the INTEGRAL Law
qt  1 t
vC t  
  iC  y dy
C
C 
 If i(t) has NO Gaps in
its i(t) curve then
1 t  t
lim vC t  t   lim  i y dy
t 0
t 0 C  
 Even if i(y) has
VERTICAL Jumps:
lim vC t  t   vC t 
t 0
Engineering-43: Engineering Circuit Analysis
8
 Thus a Major
Mathematical Implication
of the Integral law
 The Voltage Across a
Capacitor MUST be
Continuous
 An Alternative View
• The Differential Reln
dvC t 
iC t   C
dt
 If vC is NOT Continous
then dvC/dt → , and So
iC → . This is NOT
PHYSICALLYBrucepossible
Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Differential Law
 Express the CURRENT
“Thru” the Cap Using the
Differential Law
dv t 
dqt 
C C
dt
dt
 If vC = Constant Then
iC t  
iC  0
 This is the DC
Steady-State Behavior
for a Capacitor
Engineering-43: Engineering Circuit Analysis
9
 Thus a Major
Mathematical Implication
of the Differential Law
 A Cap with CONSTANT
Voltage Across it
Behaves as an OPEN
Circuit
 Cap Current
• Charges do NOT flow
THRU a Cap
– Charge ENTER or EXITS
The Cap in Response to
Voltage CHANGES
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Current
 Charges do NOT flow THRU a Cap
 Charge ENTER or EXITS The Capacitor
in Response to the Voltage Across it
• That is, the Voltage-Change DISPLACES
the Charge Stored in The Cap
– This displaced Charge is, to the
REST OF THE CKT, Indistinguishable
from conduction (Resistor) Current
 Thus The Capacitor Current is Called
the “Displacement” Current
Engineering-43: Engineering Circuit Analysis
10
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Summary
 The Circuit Symbol
iC

vC
 Note The Passive
Sign Convention

 Compare Ohm’s Law
and Capactitance Law
Cap
Ohm
iC (t )  C
t
dvc
(t )
dt
1
vC (t )   iC ( x)dx
C 
1
vR
R
vR  Ri R
iR 
Engineering-43: Engineering Circuit Analysis
11
 From Calculus, Recall an
Integral Property
t
t0
t


t0
 f x dx   f x dx   f x dx
 Now Recall the Long Form
of the Integral Relation
t
t
1 0
1
vC (t )   iC ( x)dx   iC ( x)dx
C 
C t0
 The DEFINITE Integral is
just a no.; call it vC(t0) so
t
1
vC (t )  vC (t0 )   iC ( x)dx
C t0
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Summary cont
 Consider Finally the Differential Reln
dvC t 
iC t   C
dt
 Some Implications
• For small Displacement Current dvC/dt is
small; i.e, vC changes only a little
• Obtaining Large iC requires HUGE Voltage
Gradients if C is small
 Conclusion: A Cap RESISTS
CHANGES in VOLTAGE ACROSS It
Engineering-43: Engineering Circuit Analysis
12
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
iC Defined by
Differential
 The fact that the Cap
Current is defined
through a
DIFFERENTIAL has
important
implications...
 Consider the Example
at Left
C  5F
i (t )  0 elsewhere
i (t )  C
dv
(t )
dt
 60mA
i  5 106[ F ] 
24 V 
 20mA
6 103  s 
 Using the 1st Derivative
(slopes) to find i(t)
• Shows vC(t)
– C = 5 µF
• Find iC(t)
Engineering-43: Engineering Circuit Analysis
13
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Energy Storage
 UNlike an I-src or
V-src a Cap Does
NOT Produce Energy
 For a Cap
 A Cap is a PASSIVE
Device that Can
STORE Energy
 Recall from Chp.1 The
Relation for POWER
 Recall also
p  vi

vC
iC
pC t   vC t   iC t 

dvC
iC (t )  C
(t )
dt
 Subbing into Pwr Reln
dvC
pC (t )  CvC (t )
dt
 By the Derivative CHAIN
 Then the
d
d
RULE
INSTANTANEOUS Power

d  1 2  dt dv
pC (t )  C  vC (t ) 
p t  v t i t
dt  2


 
Engineering-43: Engineering Circuit Analysis
14
C
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt

dvC
dt
Capacitor Energy Storage cont
 Again From Chp.1
Recall that Energy
(or Work) is the
time integral of Power
• Mathematically
t2
wC (t1 , t 2 )   pC ( x)dx
t1
 Comment on the Bounds
• If the Lower Bound is −
we talk about “energy
stored at time t2”
• If the Bounds are −  to
+ then we talk about the
“total energy stored”
Engineering-43: Engineering Circuit Analysis
15
 Integrating the “Chain
Rule” Relation
1 2
1 2
wC (t1 , t 2 )  CvC (t 2 )  CvC (t1 )
2
2
 Recall also
t
qC (t )
1
vC (t )   iC ( x)dx 
C 
C
 Subbing into Pwr Reln
dqC
1
pC (t )  qC (t )
(t )
dt
vC t  C
iC t 
 Again by Chain Rule d d

1 d  1 2  dt dq
pC (t ) 
 qc (t ) 
C dt  2

C
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt

dqC
dt
Capacitor Energy Storage cont.2
 Then Energy in
Terms of Capacitor
Stored-Charge
1 2
1 2
wC (t1 , t 2 )  qC (t 2 )  qC (t1 )
C
C
 Short Example
VC(t)
C = 5 µF
 The Total Energy Stored
during t = 0-6 ms
1 2
1 2
wC (0,6)  CvC (6)  CvC (0)
2
2
1
wC (0,6)  5 *10 6 [ F ] * (24) 2 [V 2 ]
2
 wC Units?
Coul 2
F V 
 V  Coul  V  J
V
2
 Charge Stored at 3 mS
qC (3)  CvC (3)
qC (3)  5 *10 6 [ F ] *12[V ]  60C
Engineering-43: Engineering Circuit Analysis
16
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Some Questions About Example
 For t > 8 mS, What is
the Total Stored
CHARGED?
vC(t)
C = 5 µF
qC (t  8mS )  0
 For t > 8 mS, What is
the Total Stored
ENERGY?
wC (t  8mS )  0
wC (, t 2 ) 
wC (, t2 ) 
1 2
1
CvC t  9   5F  0 2
2
2
DIScharging
Current
1 2
1 2
qC t2  11 
0
C
5F
Engineering-43: Engineering Circuit Analysis
17
CHARGING
Current
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Summary: Q, V, I, P, W
 Consider A Cap
Driven by A
SINUSOIDAL V-Src

 Charge stored at a Given
Time qC (t )  CvC (t )
qC 1 120  8.33mS   2 *10 6 [C ] * sin(  )[V ]  0
 Current “thru” the Cap
v (t )
i(t)
C  2 F

iC  C
dvC
(t )
dt
iC 1 120  8.33mS   2 *106 *130 *120 cos( )
v ( t )  130 sin (120 t )
iC 1 120  8.33mS   98 mA
 Energy stored at a given
time w (t )  1 Cv 2 (t )
 Find All typical Quantities
• Note
– 120 = 60∙(2) → 60 Hz
Engineering-43: Engineering Circuit Analysis
18
C
2
C
 1  1
6
2
2  
wC 
  2 *10 [ F ] *130 sin  
 240  2
2
wC  16.9 mJ
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitor Summary cont.
 Consider A Cap
Driven by A
SINUSOIDAL V-Src

v (t )
i(t)
C  2 F

v ( t )  130 sin (120 t )
 Electric power absorbed
by Cap at a given time
pC (t )  vC (t )iC (t )
Engineering-43: Engineering Circuit Analysis
19
 At 135° = (3/4)
iC 1 160  2 *106 *130 *120 cos(0.75 )
iC 1 160  69.3mA
vC 1 160  130 sin( 0.75 )  91.9V
pC 1 160  91.9V   69.3mA  6371mW
 The Cap is SUPPLYING
Power at At 135° = (3/4)
= 6.25 mS
• That is, The Cap is
RELEASING (previously)
STORED Energy at Rate
of 6.371 J/s
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
WhiteBoard Work
 Let’s Work this Problem
• The VOLTAGE across a
0.1-F capacitor is given
by the waveform in the
Figure Below. Find the
WaveForm Eqn for the
Capacitor CURRENT
vc(t)(V)
-12
0
1
2
3
4
5
t(s)
-12
Figure P5.14
ANOTHER PROB
0.5 μF
iC t   2 Acos50000t 
+ vC(t) -
Engineering-43: Engineering Circuit Analysis
20
See ENGR-43_Lec-061_Capacitors_WhtBd.ppt
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
The Inductor
 Second of the Energy-Storage Devices
 Basic Physical Model:
Ckt Symbol
 Details of Physical
Operation Described in
PHYS 4B or ENGR45
Engineering-43: Engineering Circuit Analysis
21
 Note the Use of the
PASSIVE Sign
Convention
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Physical Inductor
 Inductors are Typically Fabricated by Winding Around
a Magnetic (e.g., Iron) Core a LOW Resistance Wire
• Applying to the Terminals a TIME VARYING Current Results
in a “Back EMF” voltage at the connection terminals
 Some Real
Inductors
Engineering-43: Engineering Circuit Analysis
22
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductance Defined
 From Physics, recall
that a time varying
magnetic flux, ,
Induces a voltage
Thru the Induction
Law
d
vL 
 Where the Constant of
Proportionality, L, is called
the INDUCTANCE
 L is Measured in
Units of “Henrys”, H
• 1H = 1 V•s/Amp
 Inductors STORE
electromagnetic energy
 For a Linear Inductor The
Flux Is Proportional To
 They May Supply Stored
The Current Thru it
Energy Back To The
diL
Circuit, But They
  LiL  vL  L
CANNOT CREATE
dt
Energy
dt
Engineering-43: Engineering Circuit Analysis
23
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductance Sign Convention
 Inductors Cannot
Create Energy; They
are PASSIVE Devices
 All Passive Devices
Must Obey the
Passive Sign
Convention
Engineering-43: Engineering Circuit Analysis
24
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductor Circuit Operation
 Recall the Circuit
Representation
 Separating the Variables
and Integrating Yields
the INTEGRAL form
t
1
iL (t )   vL ( x)dx
L 
 Previously Defined the
Differential Form of the
Induction Law
diL
vL  L
dt
Engineering-43: Engineering Circuit Analysis
25
 In a development Similar
to that used with caps,
Integrate − to t0 for an
Alternative integral Law
t
1
iL (t )  iL (t0 )   vL ( x)dx; t  t0
L t0
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductor Model Implications
 From the Differential
Law Observe That if iL
is not Continuous,
diL/dt → , and vL
must also → 
 This is NOT physically
Possible
 Thus iL must be
continuous
diL
vL   

dt
Engineering-43: Engineering Circuit Analysis
26
 Consider Now the
Alternative Integral law
t
1
iL (t )  iL (t0 )   vL ( x)dx; t  t0
L t0
 If iL is constant, say iL(t0),
then The Integral MUST
be ZERO, and hence vL
MUST be ZERO
• This is DC Steady-State
Inductor Behavior
– vL = 0 at DC
– i.e; the Inductor looks like
a SHORT CIRCUIT
to DC Potentials
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductor: Power and Energy
 From the Definition of
Instantaneous Power
pL (t )  vL (t )  iL (t )
 Subbing for the Voltage
by the Differential Law
diL
p L (t )  L
(t )iL (t )
dt
 Again By the Chain Rule
for Math Differentiation
d
d di
 
dt di dt
d 1 2 
pL t    LiL (t ) 
dt  2

Engineering-43: Engineering Circuit Analysis
27
 Time Integrate Power to
Find the Energy (Work)
t2
d 1 2 
wL (t1 , t2 )    LiL ( x) dx
dx  2

t1
 Units Analysis
• J = H x A2
 Energy Stored on Time
Interval
w(t1 , t 2 ) 
1 2
1
LiL (t 2 )  LiL2 (t1 )
2
2
• Energy Stored on an Interval
Can be POSITIVE
or NEGATIVE
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductor: P & W cont.
 In the Interval Energy
Eqn Let at time t1
1 2
LiL (t1 )  0
2
 Then To Arrive At The
Stored Energy at a
later given time, t
1 2
w(t )  LiL (t )
2
 Thus Observe That the Stored Energy is
ALWAYS Positive In ABSOLUTE Terms as iL is
SQUARED
• ABSOLUTE-POSITIVE-ONLY Energy-Storage is
Characteristic of a PASSIVE ELEMENT
Engineering-43: Engineering Circuit Analysis
28
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example
 Given The iL Current
WaveForm, Find vL for
L = 10 mH
 The Derivative of a Line
is its SLOPE, m
 Then the Slopes
 10( A / s) 0  t  2ms
di 
  10( A / s) 2  t  4ms
dt 
0 elsewhere

20 103 A
 A
m

10
 s 
2 103 s
 A
m  10 
s
 And the vL Voltage
di

(t )  10( A / s)
3
  vL (t )  100 10 V  100mV
dt
L  10 10 3 H 

 The Differential Reln
diL
vL  L
dt
Engineering-43: Engineering Circuit Analysis
29
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example  Power & Energy
 The Energy Stored
between 2 & 4 mS
 The Value Is Negative
Because The Inductor
SUPPLIES Energy
PREVIOUSLY STORED
with a Magnitude of 2 μJ
 The Energy Eqn
1 2
1 2
w(2,4)  LiL (4)  LiL (2)
2
2
 Running the No.s

w(2,4)  0  0.5 *10 *103 (20 *103 ) 2
w(2,4)  2.0 µJ
Engineering-43: Engineering Circuit Analysis
30

Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Numerical Example
 Given The Voltage Wave
Form Across L , Find iL if
• L = 0.1 H
• i(0) = 2A
 The PieceWise Function
t
v(t )  2   v( x)dx  2t; 0  t  2
0
L  0.1H  i (t )  2  20t ; 0  t  2s
v(t )  0; t  2  i (t )  i (2s); t  2s
v (V )
 A Line Followed by A
Constant; Plotting
2
2 t (s)
42
i (A)
 The Integral Reln
t
1
i(t )  i(0)   v( x)dx
L0
Engineering-43: Engineering Circuit Analysis
31
2
2
t (s)
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Numerical Example - Energy
 The Current
Characteristic
42
 The Initial Stored Energy
w(0)  0.5 * 0.1[ H ](2 A) 2  0.2 J
 The “Total Stored Energy”
i (A)
w()  0.5 * 0.1[ H ] * (42 A) 2  88.2 J
 Energy Stored between 0-2
2
2
t (s)
 The Energy Eqn
w(t1 , t 2 ) 
1 2
1
LiL (t 2 )  LiL2 (t1 )
2
2
• Energy Stored on Interval
Can be POS or NEG
Engineering-43: Engineering Circuit Analysis
32
w(2,0) 
1 2
1
LiL (2)  LiL2 (0)
2
2
w(0,2)  0.5 * 0.1* (42) 2  0.5 * 0.1* (2) 2
w(0,2)  88 J
 → Consistent with Previous
Calculation
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example
w L (t )
 Find The Voltage Across
And The Energy Stored
(As Function Of Time)
v (t )
 For The Energy Stored
Engineering-43: Engineering Circuit Analysis
33
 Notice That the
ABSOLUTE Energy
Stored At Any Given
Time Is Non Negative
(by sin2)
• i.e., The Inductor Is A
PASSIVE Element
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
L = 5 mH; Find the Voltage
m
20mA
1ms
m
v  100mV
10  20
( A / s)
2 1
v  50mV
m0
v  0V
v (t )  L
m
di
(t )
dt
0  10
( A / s)
43
v  50mV
v  5 103 ( H )  20( A / s); 0  t  1ms  100mV
Engineering-43: Engineering Circuit Analysis
34
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example  Total Energy Stored
 The Ckt Below is in
the DC-SteadyState
 Shorting-Caps;
Opening-Inds
 Find the Total
Energy Stored by
the 2-Caps & 2-Inds
 KCL at node-A
 Recall that at DC
 Solving for VA
• Cap → Short-Ckt
• Ind → Open-Ckt
Engineering-43: Engineering Circuit Analysis
35
I
out
VA VA  6
 0  3 A 

3 6
6
81
VA  V  16.2V
5
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example  Total Energy Stored
 Continue Analysis of
Shorted/Opened ckt
I L1  I L 2  3 A  1.8 A  3 A
 I L1  1.2 A
 VC2 by Ohm
VC 2  I L 2  6   1.8 A 6 
 Using Ohm and
VA = 16.2V
I L2
16.2V

V  1.8 A
3  6
 By KCL at Node-A
Engineering-43: Engineering Circuit Analysis
36
 VC 2  10.8 V
 VC1 by Ohm & KVL
VC1  9V  I L1  6 
VC1  9 V   1.2A   6 
VC1  9 V  7.2 V
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example  Total Energy Stored
 Have all I’s & V’s:
−1.2 A
1.8 A
10.8 V
16.2 V
 Next using the
E-Storage Eqns
1
wC 
CVC2
2
wL

1 2
LI L
2
Engineering-43: Engineering Circuit Analysis
37
 Then the E- Storage
Calculations
wtot   wk  13.46 mJ
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Caps & Inds  Ideal vs. Real
 A Real CAP has
Parasitic
Resistances &
Inductance:
 A Real IND has
Parasitic
Resistances &
Capacitance:
Generally
SMALL
Effect
Engineering-43: Engineering Circuit Analysis
38
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Ideal vs Real
 Practical Elements “Leak”
Thru Unwanted Resistance
 Ideal C & L

i (t )
i (t )
i (t )
i (t )


v (t )


v (t )

v (t )
v (t )


dv
di
i (t )  C (t ) v (t )  L (t )
dt
dt
Engineering-43: Engineering Circuit Analysis
39
v (t )
dv
i (t ) 
 C (t )
Rleak
dt
v (t )  Rleak i (t )  L
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
di
(t )
dt
Capacitors in Series
 By KVL for 1-LOOP ckt
 If the vi(t0) = 0, Then
Discern the Equivalent
Series Capacitance, CS
 CAPS in SERIES
Combine as Resistors
in PARALLEL
Engineering-43: Engineering Circuit Analysis
40
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example
 Find
 Spot Caps in Series
• Equivalent C
• Initial Voltage
1 1 1 1 3  2 1
   
 CS  1
CS 2 3 6
6
1 F
 Or Can Reduce
Two at a Time
 Use KVL for Initial Voltage
vt0   2V  4V  1V  3V
2 F
 This is the Algebraic Sum
of the Initial Voltages
• Polarity is Set by the
Reference Directions
noted in the Diagram
Engineering-43: Engineering Circuit Analysis
41
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Numerical Example
 Two charged
Capacitors Are
Connected As Shown.
 Find the Unknown
Capacitance

8V
+
-
12V
30  F


4V

C
Engineering-43: Engineering Circuit Analysis
42
 Recognize SINGLE Loop
Ckt → Same Current in
Both Caps
• Thus Both Caps Accumulate
the SAME Charge
Q  (30 F )(8V )  240C
 And Find VC by KVL
• VC = 12V-8V = 4V
 Finally Find C by
Charge Eqn
QC 240 μC
C

 60 μC
VC
4V
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Capacitors in Parallel
 By KCL for 1-NodePair ckt  Thus The Equivalent
Parallel Capacitance
 CAPS in Parallel
Combine as Resistors
in SERIES
Engineering-43: Engineering Circuit Analysis
43
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Complex Example → Find Ceq
6 F
3 F
C eq 
3
C eq   F
2
2 F
Engineering-43: Engineering Circuit Analysis
44
4 F
4 F
12  F
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
3 F
Inductors in Series
 By KVL For 1-LOOP ckt
 Use The Inductance Law
di
vk (t )  Lk (t )
dt
 Thus
di
v (t )  LS (t )
dt
 INDUCTORS in Series
add as Resistors
in SERIES
Engineering-43: Engineering Circuit Analysis
45
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductors in Parallel
 By KCL for 1-NodePair ckt  And
 Thus
N
i (t0 )   i j (t0 )
j 1
 INDUCTORS in Parallel
combine as Resistors
in PARALLEL
Engineering-43: Engineering Circuit Analysis
46
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Example – Find: Leq, i0
4mH
2mH
i (t0 )  3 A  6 A  2 A  1A
 Series↔Parallel Summary
• INDUCTORS Combine as do RESISTORS
• CAPACITORS Combine as do CONDUCTORS
Engineering-43: Engineering Circuit Analysis
47
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Inductor Ladder Network
 Find Leq for Li = 4 mH
 Place Nodes In Chosen
Locations
a
 Connect Between Nodes
6mH
a 4mH
d
4mH
2mH
c
Leq
c
d
2mH
2mH
b
2mH
 When in Doubt, ReDraw
• Select Nodes
Engineering-43: Engineering Circuit Analysis
48
b
Leq  (6mH || 4mH )  2mH  4.4mH
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Find Leq for Li = 6mH
a
 ReDraw The Ckt for
Enhanced Clarity
a
6 || 6 || 6
2mH
b
Leq
• The Electrical Diagram
Does NOT have to Follow
the Physical Layout
Engineering-43: Engineering Circuit Analysis
49
6mH
6mH
c
 Nodes Can have
Complex Shapes
b
6mH
c
 It’s Simple Now
Leq  6  (6  2) || 6  6 
48
24
 6 mH
14
7
66
Leq 
mH
7
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
C&L Summary
Engineering-43: Engineering Circuit Analysis
50
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
WhiteBoard Work
 Let’s Work This Problem
L  50 H
i t   0
it   2te 4t
t0
t 0
 Find: v(t), tmax for imax, tmin for vmin
Engineering-43: Engineering Circuit Analysis
51
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
% Bruce Mayer, PE * 14Mar10
% ENGR43 * Inductor_Lec_WhtBd_Prob_1003.m
%
t = linspace(0, 1);
%
iLn = 2*t;
iexp = exp(-4*t);
plot(t, iLn, t, iexp), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
%
i = 2*t.*exp(-4*t);
plot(t, iLn, t, iexp, t, i),grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
plot(t, i), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
vL_uV =100*exp(-4*t).*(1-4*t);
plot(t, vL_uV)
i_mA = i*1000;
plot(t, vL_uV, t, i_mA), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
%
% find mins with fminbnd
[t_vLmin vLmin] = fminbnd(@(t) 100*exp(-4*t).*(1-4*t), 0,1)
% must "turn over" current to create a minimum
i_mA_TO = -i*1000;
plot(t, i_mA_TO), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
[t_iLmin iLmin_TO] = fminbnd(@(t) -1000*(2*t.*exp(-4*t)), 0,1);
t_iLmin
iLmin = -iLmin_TO
plot(t, vL_uV, t, i_mA, t_vLmin, vLmin, 'p', t_iLmin,iLmin,'p'), grid
Engineering-43: Engineering Circuit Analysis
52
By
MATLAB
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
% Bruce Mayer, PE * 14Mar10
% ENGR43 * Inductor_Lec_WhtBd_Prob_1003.m
%
t = linspace(0, 1);
%
iLn = 2*t;
iexp = exp(-4*t);
plot(t, iLn, t, iexp), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
%
i = 2*t.*exp(-4*t);
plot(t, iLn, t, iexp, t, i),grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
plot(t, i), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
vL_uV =100*exp(-4*t).*(1-4*t);
plot(t, vL_uV)
i_mA = i*1000;
plot(t, vL_uV, t, i_mA), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
%
% find mins with fminbnd
[t_vLmin vLmin] = fminbnd(@(t) 100*exp(-4*t).*(1-4*t), 0,1)
% must "turn over" current to create a minimum
i_mA_TO = -i*1000;
plot(t, i_mA_TO), grid
disp('Showing Plot - Hit ANY KEY to Continue')
pause
[t_iLmin iLmin_TO] = fminbnd(@(t) -1000*(2*t.*exp(-4*t)), 0,1);
t_iLmin
iLmin = -iLmin_TO
plot(t, vL_uV, t, i_mA, t_vLmin, vLmin, 'p', t_iLmin,iLmin,'p'), grid
By
MATLAB
Engineering-43: Engineering Circuit Analysis
53
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
200
150
100
50
0
-50
0
0.1
0.2
0.3
Engineering-43: Engineering Circuit Analysis
54
0.4
0.5
0.6
0.7
0.8
0.9
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
1
Irwin Prob 5.26: I(t) & v(t)
200
i(t) (mA)
175
Current (mA)
150
125
100
75
50
25
0
-0.1
0.0
0.1
0.2
file = Engr44_prob_5-26_Fall03..xls
Engineering-43: Engineering Circuit Analysis
55
0.3
0.4
0.5
0.6
0.7
0.8
0.9
time (s)
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
1.0
Irwin Prob 5.26: I(t) & v(t)
200
120
i(t) (mA)
v(t) (µV)
100
150
80
125
60
100
40
75
20
50
0
25
-20
0
-0.1
-40
0.0
0.1
0.2
file = Engr44_prob_5-26_Fall03.xls
Engineering-43: Engineering Circuit Analysis
56
0.3
0.4
0.5
0.6
0.7
0.8
0.9
time (s)
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
1.0
Electrical Potential (µV)
Current (mA)
175
L = 10 mH; Find the Voltage
v  100mV
v (t )  L
20 103  A 
v  10 10 [ H ] 
2 103  s 
3
Engineering-43: Engineering Circuit Analysis
57
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
di
(t )
dt
Engineering 43
Appendix
Complex Cap
Example
Bruce Mayer, PE
Licensed Electrical & Mechanical Engineer
[email protected]
Engineering-43: Engineering Circuit Analysis
58
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Numerical Example
 Given iC, Find vC
 The Piecewise Fcn for iC
C= 4µF
vC(0) = 0
>
3
v (t )  2t  8 10 [V ]
2  t  4ms
 Integrating & Graphing
1t
v (t )  v (0)   i ( x )dx; t  0
C0
Linear
0t 2
1t
v (t )  v (2)   i ( x )dx; t  2
C2
Engineering-43: Engineering Circuit Analysis
59
Parabolic
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Power Example
 From Before the vC
 For The Previous
Conditions,
Find The POWER
Characteristic
• C = 4 µF
• iC by Piecewise curve
i (t )  8 103 t
 Using the Pwr Reln
p(t )  8t 3 , 0  t  2ms
p(t )  0, elsewhere
Engineering-43: Engineering Circuit Analysis
60
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
2  t  4ms
Power Example cont
 Finally the Power
Characteristic
 Absorbing or
Supplying Power?
 During the
CHARGING Period
of 0-2 mS, the Cap
ABSORBS Power
 During DIScharge
the Cap
SUPPLIES power
• But only until the
stored charge is fully
depleted
Engineering-43: Engineering Circuit Analysis
61
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Energy Example
 For The Previous
Conditions, Find The
ENERGY Characteristic
 Now The Work
(or Energy) is the
Time Integral of Power
• C = 4 µF
• pC by Piecewise curve
 For 0  t  2 mS
p(t )  8t 3
Engineering-43: Engineering Circuit Analysis
62
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Energy Example cont
 For 2 < t  4 mS
2t 4
8  t 2  64n  t  128 p
 Taking The Time Integral
and adding w(2 mS)
 Then the Energy
Characteristic
Engineering-43: Engineering Circuit Analysis
63
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
If the current is known ...
SAMPLE PROBLEM
Current through capacitor
iC

vC
C
e 0.5t ; t  0
iC (t )  
[mA]
 0; t  0

C  2F
t
Voltage at a given time t
1
vC (t )   iC ( x)dx
C 
vC (0)  0[V ]
Voltage at a given time t when voltage at time to<t is also known
2
1
1 0.5 x

v
(
0
)

e
dx
vC (2)  C
2 *106
C 0
Charge at a given time
2
1
1
 1 0.5 x 
1
6



1

e

0
.
6321
*
10

e
V

6
 0.5
 2 *10 0.5
0
qC (t )  CvC (t )
qC (2)  2 * 0.6321
t
Voltage as a function of time
vC (t ) 
Electric power supplied to capacitor
1
iC ( x)dx

C 
Energy stored in capacitor at a given time w (t ) 
64
vC (t )  0; t  0
pC (t )  vC (t )iC (t )
“Total”Engineering-43:
energy stored
in the
capacitor
Engineering
Circuit
Analysis
t
1
vC (t )  vC (t0 )   iC ( x)dx
C t0
W
1 2
CvC (t ) J
2
1
wT  CvC2 ()
2
C
t
1
vC (t )  vC (0)   e 0.5 x dx
C0
106 (1  e 0.5t ); t  0
vC (t )  
0; t  0

1
wT  2 *106 * Bruce
(106Mayer,
) 2  PE
106
2
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
J
V
SAMPLE PROBLEM
Given current and capacitance
Compute voltage as a function of time
At minus infinity everything is zero. Since
current is zero for t<0 we have
0  t  5m sec 
VC (0)  0  VC (t ) 
5
10
VC (t )  0; t  0
15 A
106 A
iC (t ) 
t  3 3 t  3 *103[ A / s] t
5 ms
10 s
3 t
3
3 *10
xdx [V ]  3 *10 t 2 [V ]; 0  t  5 *103[ s ]
6 
4 *10 0
8
In particular
3 *103 * (5 *103 ) 2
75
VC (5ms) 
[V ]  [mV ]
8
8
t (m sec)
5  t  10 ms  iC (t )  10 [A]
t
75
75 *103
1
VC (5ms )  [mV ]  VC (t ) 

(10 *106 )[ A / s]dx
6 
8
8
4 *10 5*103
Charge stored at 5ms
qC (t )  CVC (t )
75 *103
q(5ms)  4 *10 [ F ] *
[V ]
8
6
q(5ms)  (75 / 2) [nC ]
75 *103 10
VC (t ) 

t  5 *103 [V ]; 5 *103  t  10 *103 [ s]
8
4

Total energy stored
1
E  CVC2
2
Total means at infinity. Hence
2

Before looking into a formal way to describe the current
we will look at additional questions that can be answered.
3

 Circuit Analysis
25
*
10

6
Bruce Mayer, PE
 [ J ]
ET  0.5Engineering-43:
* 4 *10  Engineering
Now, for a formal way to represent piecewise
functions....
65
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
8


Formal description of a piecewise analytical signal
0;

 3 2
t ;

8

Vc (t )   75 10
 t  5;
8 4

25
 ;

8

t0
0  t  5ms
5  t  10 [ms]
t  10[ms]
Engineering-43: Engineering Circuit Analysis
66
[mV ]
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
Find Ceq for Ci = 4 µF
8 F
8 F
4 F
48
C eq
8
32
8 
3
3
Engineering-43: Engineering Circuit Analysis
67
32
F
12
8 F
Bruce Mayer, PE
[email protected] • ENGR-43_Lec-06-1_Capacitors.ppt
8 F