Download Part I

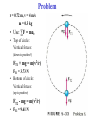
Chapter 6: Circular Motion & Other
Applications of Newton’s Laws
Recall a Ch. 4 Result
The Acceleration of a Mass Moving in Circle
(At Constant Speed)
Consider a particle moving in a circle
of radius r, at a constant speed v.
The velocity vector is tangent to the
circle. There is a Centripetal
Acceleration, a = ac. The acceleration
vector is directed radially inward.
 ac  v always
ac = (v2/r)
Newton’s Laws + Circular Motion
Centripetal Acceleration
ac = (v2/r)  v
By Newton’s 1st Law
There must be a net force acting.
By Newton’s 2nd Law:
∑F = ma = mac = m(v2/r)
(magnitudes)
Direction
The total force ∑F
must be radially inward.
• For a particle moving in uniform circular motion around
a circle of radius r (speed v = constant): The acceleration is:
ac = (v2/r), ac  v always!!
ac is radially inward always!
• By Newton’s 1st Law:
There must be a force acting!
• By Newton’s 2nd Law:
∑F = ma  Fr = mac= m(v2/r)
The total force ∑F must be radially inward always!
 The total force on the right side of
Newton’s 2nd Law  The Centripetal Force ∑F  Fr
(A center directed force)
• Fr is NOT a new kind of force. Exactly what it is depends on the
problem. It could be string tension, gravity, etc. It is the right side
of ∑F = ma, not the left side! (It is the form of ma for circular motion)
• A particle moving in uniform
circular motion, radius r (speed
v = constant):
• The Centripetal Acceleration:
aR = (v2/r) , aR  v always!!
aR is radially inward always!
Newton’s 1st Law:
• Says that there must be a
force acting!
Newton’s 2nd Law:
• Says that
∑F = ma = maR = m(v2/r)
(magnitude)
• Direction: The total force must
be radially inward always!
For an object to be in uniform
circular motion,
There Must be a Net
Force Acting on it.
We already know the
acceleration, so we can
immediately write the force:
Centripetal Force
You can see that the centripetal
force must be inward by thinking
about the ball on a string. Strings
only pull; they never push!!
MISCONCEPTION!!
The force on the ball is NEVER
Outward (“Centrifugal”). It is
ALWAYS inward (Centripetal) !!
Example: A ball twirled on a string in a
circle at constant speed. The centripetal
force Fr is the tension in the string.
MISCONCEPTION!!
The force on the ball is NEVER
outward (“centrifugal force”).
The force on the ball is ALWAYS
inward (centripetal force).
An outward force (“centrifugal”) is
NOT a valid concept!
The force ON THE BALL is
inward (centripetal).
What happens when the ball is released?
(Fr = 0). Newton’s 1st Law says it
should move off in a straight
line at constant v.
An outward force
(“centrifugal force”) is
NOT
a valid concept!
The force
ON THE BALL
is inward (centripetal).
Note!!
Example 6.1: Conical Pendulum
A ball, mass m, is suspended from
a string of length L. It revolves
with constant speed v in a
horizontal circle of radius r. The
angle L makes with the horizontal
is θ. Find an expression for v.
T ≡ tension in the string. Fig. (b) shows horizontal & vertical
components of T:
Tx = Tsinθ, Ty = Tcosθ.
Newton’s 2nd Law: ∑Fx = Tsinθ = mac= m(v2/r) (1)
∑Fy = Tcosθ – mg = 0; Tcosθ = mg
(2)
Dividing (1) by (2) gives: tanθ = [v2/(rg)] , or v = (rg tanθ)½
From trig, r = L sinθ so, v = (Lg sinθ tanθ)½
(Reminder: ½ power means the square root)
Example 6.3: Car Around a Curve
Curve radius: r = 35 m. Static friction coefficient
between tires & road: μs = 0.523. The centripetal
force that keeps the car on the road is the static
friction force fs between the tires & the road.
Calculate the maximum speed vmax for the car to
stay on the curve. Free body diagram is (b).
Newton’s 2nd Law
(let + x be to left) is:
∑Fx = fs = mac = m(v2/r) (1)
∑Fy = 0 = n – mg; n = mg (2)
The maximum static friction force is (using (2))
fs(max) = μsn = μsmg
(3)
 If
m(v2/r) > fs(max), so vmax is the
solution to μsmg = m[(vmax)2/r]
vmax = (μsgr)½
Putting in numbers gives: vmax = 13.4 m/s
Or,
Example 6.4: Banked Curves
Engineers design curves which are banked
(tilted towards the inside of the curve) to keep cars
on the road. If r = 35 m & we need
v = 13.4 m/s, calculate the angle θ of
banking needed (without friction). From free
body diagram, the horizontal (radial) &
vertical components of the force n normal
to the surface are:
nx = n sinθ, ny = n cosθ,
Newton’s 2nd Law
∑Fx = n sinθ = m(v2/r)
(1)
∑Fy = 0 = n cosθ – mg; n cosθ = mg (2)
Dividing (1) by (2) gives: tanθ = [(v2)/(gr)]
Putting in numbers gives: tanθ = 0.523 or
θ = 27.6°
Example: “Loop-the-Loop”!
A pilot, mass m, in a jet does a
“loop-the-loop. The plane, Fig. (a),
moves in a vertical circle, radius
r = 2.7 km = 2,700 m at a constant
speed v = 225 m/s.
a) Calculate the force, nbot (normal force),
exerted by the seat on the pilot at the
bottom of the circle, Fig. (b).
b) Calculate this force, ntop, at the top
of the circle, Fig. (c).
TOP: Fig. (b). Newton’s 2nd Law in the radial (y) direction (up is “+”).
∑Fy = nbot – mg = m(v2/r) so nbot = m(v2/r) + mg or
nbot = mg[1 + (v2/rg)] = 2.91 mg (putting in numbers) he feels “heavier”.
BOTTOM: Fig. (c). Newton’s 2nd Law in the radial (y) direction (down is “+”).
∑Fy = ntop + mg = m(v2/r) so ntop = m(v2/r) - mg or
ntop = mg[(v2/rg) - 1] = 0.913 mg (putting in numbers) he feels “lighter”.
Example (Estimate)
m = 0.15 kg, r = 0.6 m, f = 2 rev/s  T = 0.5 s
Assumption: Circular path is  in horizontal plane,
so θ  0  cos(θ)  1
Newton’s 2nd Law: ∑F = ma
 FTx = max= mac = m(v2/r)
v =(2πr/T) = 7.54 m/s
FTx = 14 N (tension)
Example
Problem
r = 0.72 m, v = 4 m/s
m = 0.3 kg
• Use: ∑F = mac
• Top of circle:
Vertical forces:
(down is positive!)
FT1 + mg = m(v2/r)
FT1 = 3.73 N
• Bottom of circle:
Vertical forces:
(up is positive)
FT2 - mg = m(v2/r)
• FT2 = 9.61 N
Example
n
n