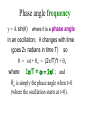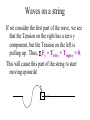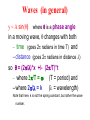Download Part51

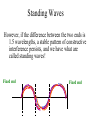
Vibrations and Oscillations
A mass on a spring will oscillate if the mass is
pushed or pulled from its equilibrium position.
Why?
We saw from the Hooke’s Law experiment that the
force of a spring is related to how far the spring is
pulled or pushed from equilibrium:
Fspring = -k(x-xo)
where the minus simply indicates that if you
push in on the spring, the spring pushes out.
Springs
The spring constant, k, describes how “stiff”
the spring is. A large k indicates that a
large force is needed to stretch the spring.
But why does the mass oscillate?
From Newton’s Second Law, if we ignore
other forces like friction or air resistance:
 F = ma and ΣF = -k(y-yo) - mg leads to
-k(y-yo) - mg = ma .
(in the force of the spring, we have replaced x with y since the mass
will be going up and down instead of left and right)
Oscillations of Springs
-k(y-yo) - mg = ma
This says that if y-yo is negative (spring stretched below
equilibrium point, yo), the force is positive (directed up)
and hence the acceleration is positive. This will
produce a velocity that, if initially zero, will become
positive, tending to reduce the negative y-yo. As y
approaches the equilibrium position, the force
approaches zero and the acceleration will approach
zero; but this still leaves a positive velocity!
Oscillations of Springs
Now as it passes the equilibrium position, the mass
has velocity so it will pass through the equilibrium
position and end up with a positive (compressed)
position. Here the force becomes negative giving
a negative acceleration. This will make the
positive velocity less positive, but still positive.
Hence the mass will go to an even more positive
position, with an even bigger negative force and
acceleration that will continue to slow it down
until it reaches zero speed.
Oscillations of Springs
At this point where the speed is zero, we have
a positive (compressed) position which
gives a negative force and hence negative
acceleration. This acceleration will then
cause the speed to decrease to a negative
value which will cause the mass to move
back towards equilibrium.
This process continues and we get an
oscillation!
Formulas for Oscillations
From the calculus, we can solve
-k(y-yo) - mg = ma = m d2y/dt2
(this is a differential equation) to get:
y = yo – mg/k + A sin(wt + qo) = ye + A sin(wt + qo) ,
(where ye = yo – mg/k is the new equilibrium position)
This should appear reasonable: the sine function
oscillates (goes up and down in value) just like the
mass oscillates! But the sine function needs an
angle to operate on! Where is the angle in the
problem?
Angles: geometric and phase
y = ye + A sin(wt + qo)
The sine function is operating on the quantity:
(wt + qo). This expression must be an angle. But
what angle?
There is no “geometric” angle in the problem
because the problem is only in one dimension.
Instead, we call this kind of angle a phase angle. A
phase angle simply describes where in the
oscillation the wave is!
Sine and Phase Angles
Sine function
Value of
sine
The crest of the
sine wave is
located at 90o,
the trough at 270o
and it crosses zero
at 0o, 180o and
starts repeating
at 360o
(or 2p radians).
1
0
-1
Phase angle in degrees
Series1
Phase angle frequency
y = A sin(q)
where q is a phase angle
in an oscillation; q changes with time
(goes 2p radians in time T) so
q = wt + qo = (2p/T)*t + qo
where
2p/T = w = 2pf ; and
qo is simply the phase angle when t=0
(where the oscillation starts at t=0).
Amplitude
y = ye + A sin(wt + qo) .
The amplitude, A, describes how far up and
how far down y goes. Since sine has a
maximum value of 1 and a minimum value
of -1, A is used to put in units and give the
amplitude of the oscillation.
What does w depend on?
y = A sin(wt + qo)
We have seen that w describes how fast the mass
oscillates. But what does this oscillation speed
(ω = dqphase/dt ) depend on?
By putting in our solution for y into Newton’s
Second Law (the differential equation), we can get
a prediction:
w = (k/m) .
For stiffer springs and lighter masses, the frequency
of the oscillation increases.
Note: the Amplitude does NOT affect the frequency!
Oscillations and Energy
For masses on springs, we have:
Etotal = KE + PE = (1/2)mv2 + (1/2)kx2 .
We also know that x = A sin(wt + qo) .
If we look at how x changes with time, we get
the speed. From the calculus, we get:
v = wA cos(wt + qo) . Therefore, Etotal =
(1/2)mw2A2cos2(wt+qo) + (1/2)kA2sin2 (wt+qo) .
Note: when sine is maximum, cosine is zero;
and when sine is zero, cosine is maximum!
Oscillations and Energy
Etotal =
(1/2)mw2A2cos2(wt+qo) + (1/2)kA2sin2 (wt+qo) .
From the above, it looks like Etotal depends on
time. Does this violate Conservation of
Energy?
We saw that w = (k/m) . Substituting this into
the first term gives: Etotal =
(1/2) kA2cos2(wt+qo) + (1/2)kA2sin2 (wt+qo)
= (1/2)kA2 = (1/2) mw2A2, which does NOT
depend on time!
Energy: Amplitude and frequency
Since Energy = (1/2) mw2A2 , as the frequency
goes up (ω), to keep the same energy the
amplitude (A) needs to go down. Can you make
sense of that relationship?
Since kinetic energy depends on velocity (squared),
and since v = dx/dt , a higher frequency means
that for the same distance (amplitude) we have a
smaller dt. To keep the same v, we need a smaller
distance (amplitude) to go with the smaller dt
(higher frequency).
Springs and Applied Force
If we pull the mass on the spring (giving it
potential energy), then release the mass, the
mass will oscillate:
y = ye + A sin(wt + qo)
at a frequency: w = (k/m). The initial
energy we put into the system went into the
potential energy of the spring. When we let
loose, the energy oscillates between
potential energy and kinetic energy (until
friction bleeds the energy away).
Springs and Applied Force
What happens when we continue to apply a
force on the mass? Specifically, what
happens when we apply an oscillating force:
Fapplied = Fo sin(wappliedt) ?
How does the mass on the spring respond?
Does it’s response depend on Fo ?
Does it’s response depend on wapplied ?
We’ll see a demonstration in class.
Resonance
As we saw in the demonstration, the mass on
the spring does not receive much energy
from the oscillating force, unless wapplied is
very close to wfree . This is because the
force is sometimes in the same direction as
the motion (giving energy) and sometimes
in the opposite direction (receiving energy),
so on average very little energy is actually
transmitted.
Resonance
When wapplied = wfree , we have a lot of energy
transferred from the oscillating force into
the mass/spring system, because the force is
always in the direction of the motion. We
call this resonance.
Whenever we have something that oscillates,
we will find resonance. We will run into
many examples where resonance is very
important.
The Pendulum
In the Oscillations Lab, we will
experimentally develop equations to
describe the oscillations of a pendulum.
In this case, we will have a real geometric
angle AND we will have a phase angle.
The geometric angle (the angle the pendulum
makes with the vertical) oscillates, so we will
have:
qpendulum = qmax sin(wt+fo) .
The Pendulum
In the lab we will investigate what physical
parameters the period (T) depends on.
Again, we will have the relations we had for
the spring and for circular motion in
general:
f = 1/T, w=2pf .
Waves on a string
If you wiggle one end of a string (or slinky)
that has a tension on it, you will send a
wave down the string. Why? How fast
does the wave travel? What is moving in
the wave?
We can consider this by looking at Newton’s
Second Law:
Waves on a string
If we consider the first part of the wave, we see
that the Tension on the right has a zero y
component, but the Tension on the left is
pulling up. Thus,  Fy = Tleft-y + Tright-y > 0.
This will cause this part of the string to start
moving upwards!
Waves on a string
A little later, this part of the string is moving
upwards, but now the Tension on the left
has less of a y component and the Tension
on the right has a bigger negative y
component! This will tend to slow this part
of the string down!
Waves on a string
At the top of the pulse, the wave has slowed
to zero, but both the left and right Tensions
are pulling down, so there will continue to
be a negative y force, and this will cause
this part of the string to start moving down.
Waves on a string
By continuing to look at each part of the
string, we can understand how the wave can
move down the string.
Using the calculus, we can solve the
differential equation that Newton’s Law
gives, and we get:
y = A sin(kx  wt) .
Waves (in general)
y = A sin(q) where q is a phase angle
in a moving wave, q changes with both
– time (goes 2p radians in time T) and
– distance (goes 2p radians in distance )
so q = (2p/)*x +/- (2p/T)*t
– where 2p/T = w
(T = period) and
– where 2p/ = k
( = wavelength)
Note that here, k is not the spring constant, but rather the wave
number.
Speed of the wave
(phase speed)
What is moving in the wave?
Each part of the slinky is just moving up and down.
We can see that the crest of the wave is moving
along the length of the slinky, and we can describe
the crest with a phase angle (crest is where phase angle =
90o), so Speed of wave = phase speed =
v = distance/time = /T = f = w/k.
Note that the phase speed is not the same as the speed of material
that is moving up and down.
Waves (in general)
• sine waves are nice - for nice sine waves:
y = A sin(kx  wt + qo)
• other types of waves (such as square waves, sawtooth
waves, etc.) can be formed by a superposition of sine
waves - this is called Fourier Series . This
means that sine waves can be considered as
fundamental.
The process of breaking a wave into its component
sine waves is called spectral analysis.
Waves on a String
By continuing the analysis using Newton’s
Second Law and the calculus, we can come
up with relations for the phase speed of the
wave in terms of the parameters of the
wave:
v = f = w/k = (Ttension)/m)
where m = m/L (mass/length of string).
Caution: don’t confuse the symbol, T, for period with the symbol, T, for
tension.
Caution: don’t confuse the symbol, k, for spring constant with the
symbol, k, for wave number.
Power delivered by a wave
Each part of a nice sine wave oscillates just
like a mass on a spring. Hence it’s energy
is that of an oscillating mass on a spring.
We saw before that this depended on w2A2.
The power delivered by a wave is just this
energy per time. The rate of delivery
depends on the speed of the wave. Thus the
power in the wave should depend on:
P  w2A2v where  means proportional to.
Reflections of Waves
Do waves “bounce” off of obstacles? In other words, do
waves reflect?
We observed this in lab and/or in a class demo with a
slinky.
There are two cases:
1. when waves bounce off a stiff obstacle, the waves
do reflect, but they change phase by 180o;
2. when waves bounce off a loose obstacle, the waves
do reflect, but they do NOT change phase.
Interference: Waves on a String
When a wave on a string encounters a fixed end, the
reflected wave must interfere with the incoming wave so
as to produce cancellation. This means the reflected
wave is 180 degrees (or /2) out of phase with the
incoming wave at the fixed end. The image below
shows a picture of the blue incoming wave and the red
reflected wave at one particular instant. At this instant, the
two waves add to zero at the right end, but the two troughs
near the right end add together!
Fixed end
Interference: Waves on a String
Below is the same situation, only this time we
picture the situation at a time (1/4)T later.
Note that the blue incoming wave is at a
trough and the red reflected wave is at a
crest and so the two cancel at the fixed end
as required. Note that at this instant, we get
cancellation everywhere!
Fixed end
Interference: Waves on a String
Below is the same situation, and this time we
picture the situation at a time (1/4)T later
than the previous, or (1/2)T later than the
first. Note that both the blue incident wave
and the red reflected wave are at zero at the
fixed end, but the two crests near the right
end add constructively!
Fixed end
Interference: Waves on a String
When a wave on a string encounters a free
end, the reflected wave does NOT have to
destructively interfere with the incoming
wave since there is no requirement that the
end stays at zero. There is NO phase shift
on this reflection.
Free end
Interference: Waves on a String
Again, we picture the situation at a time
(1/4) T later. The incident wave is at a
trough and the reflected wave is also at a
trough at the free end.
Free end
Interference: Waves on a String
Below is the same situation, and this time we
picture the situation at a time (1/4)T later
than the previous, or (1/2)T later than the
first.
Free end
Below is the situation with two fixed ends spaced 1.625 wavelengths
apart (phase difference of 585o which is the same as 225o).
1. The blue is the incident wave arriving at the right end with a
phase of 180o and is reflected.
2. The red is the first reflected wave from the right end starting
with a phase of 180o+180o = 360o which is the same as 0o. The
red wave reaches the left end with a phase of 225o and is
reflected.
3. The purple reflected wave starts with a phase of 225o+180o =
405o which is the same as 45o. It reaches the right end with a
phase of 45o+225o = 270o and is reflected.
4. The orange reflected wave starts with a phase of 270o+180o =
450o which is the same as 90o.
Fixed end
Fixed end
Interference
Notice how confused the waves become, and when
you start adding them all together, you tend to
get cancellation everywhere all the time.
Fixed end
Fixed end
Standing Waves
However, if the difference between the two ends is
1.5 wavelengths, a stable pattern of constructive
interference persists, and we have what are
called standing waves!
Fixed end
Fixed end
Standing Waves
To create what are called standing waves (we will play
with these in the last lab), we need to create
constructive interference from both ends. This leads
to the following condition: #(/2) = L ,
which says: we need an integer number of half
wavelengths to “fit” on the Length of the string for
standing waves.
We can vary the wavelength by either varying the frequency or
the speed of the wave: recall that phase speed: v =
distance/time = /Tperiod = f . For a wave on a string,
recall that v = f = (Ttension)/m) where m = m/L.
Standing Waves
For stringed instruments (piano, guitar, etc.), the string
vibrates with both ends fixed. However, with
wind instruments (trumpet, trombone, etc.), we can
have the situation where both ends are free and a
different situation where one end is free and one
end is fixed.
1. If both ends are free, we get the same resonance
condition as for both ends fixed: #(/2) = L.
2. If one end is free and the other end is fixed, we
get a different condition: #odd(/4) = L, where
#odd is an odd number (1, 3, 5, etc.).
Interference: Waves on a String
In general:
• When a wave is incident on a SLOWER
medium, the reflected wave is 180 degrees
out of phase with the incident wave.
• When a wave is incident on a FASTER
medium, the reflected wave does NOT
undergo a 180 degree phase shift.