Download ch 13 - Simple Harmonic Motion

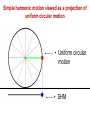
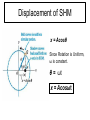
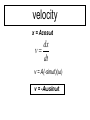
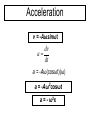
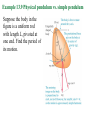
Chapter 13
Periodic Motion
PowerPoint® Lectures for
University Physics, Twelfth Edition
– Hugh D. Young and Roger A. Freedman
Lectures by James Pazun
Copyright © 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley
Goals for Chapter 13
• To outline periodic motion
• To quantify simple harmonic motion
• To explore the energy in simple harmonic motion
• To consider angular simple harmonic motion
• To study the simple pendulum
• To examine the physical pendulum
Copyright © 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley
13.1 Describing oscillations
• The spring drives the
glider back and forth on
the air-track and you
can observe the changes
in the free-body
diagram as the motion
proceeds from –A to A
and back.
Characteristics of periodic motion
• equilibrium position:
• Fnet = 0
•a=0
• v is max
• KE is max
• PEs is min
• Restoring force
Fs = - kx
• E = PEs + K = constant
Amplitude, Period, Frequency, and Angular Frequency
• The amplitude of the motion, denoted by A, is the
maximum magnitude of displacement from equilibrium or
the maximum of |x|.
• The period, T, is the time for one cycle. It is always positive.
Its SI unit is second.
• The frequency, f, is the number of cycles in a unit of time. It
is always positive, its SI units is hertz: 1 Hz= 1 s-1
• The angular frequency, ω, is 2π times the frequency:
ω = 2πf
• The relationships between frequency and period:
f = 1/T
T = 1/f
• For angular frequency: ω = 2πf = 2π/T
Example 13.1 Period, frequency, and angular frequency
An ultrasonic transducer used for medical diagnosis oscillates
at a frequency of 6.7 MHz. How much time does each
oscillation take, and what is the angular frequency?
Test Your Understanding 13.1
• For each of the following values of the body’s xvelocity vx and x-acceleration ax, state whether
its displacement x is positive, negative, or zero.
1. vx > 0 and ax > 0
negative
2. vx > 0 and ax < 0
positive
3. vx < 0 and ax > 0
negative
4. vx < 0 and ax < 0
positive
5. vx = 0 and ax < 0
positive
6. vx > 0 and ax = 0
zero
x>0
x=0
x<0
13.2 Simple harmonic motion
• When the restoring force Fx is directly proportional to the
displacement from equilibrium x, such as:
Fx  kx
• the oscillation is called simple harmonic motion, or SHM.
Fx  kx
k
ax 

 x
m
m
m
The minus sign means the acceleration and displacement
always have opposite signs.
This acceleration is not constant, so we can’t use the
constant acceleration equations.
Object moving on an ideal
spring, the motion is SHM
Simple harmonic motion viewed as a projection of
uniform circular motion
• Uniform circular
motion
• SHM
Displacement of SHM
x = Acosθ
Since Rotation is Uniform,
ω is constant.
θ = ωt
x = Acosωt
velocity
x = Acosωt
dx
v
dt
v = A(-sinωt)(ω)
v = -Aωsinωt
Acceleration
v = -Aωsinωt
dv
a
dt
a = -Aω(cosωt)(ω)
a = -Aω2cosωt
a = - ω 2x
a=-
2
ωx
• The acceleration of the point P is directly
proportional to the displacement x and
always has the opposite sign –
hallmarks of simple harmonic
motion.
• Comparing equations:
k
ax   x
m
• We get:
k
 
m
2
a x   2 x
k

m
Note: ω is the angular speed of Q (circular motion) and the
angular frequency of SHM. These quantities are equal!
When you start a body oscillating in SHM, the value of angular
frequency ω is not yours to choose; it is predetermined by the
values of k and m. the units k are N/m or kg/s2, so the unit of ω is
rad/s.
• Correspondingly, we have frequency and period as:

1
f 

2 2
k
m
1
m
T   2
f
k
The equation shows that an object with a larger mass m, greater
inertia, will have less acceleration, move less frequently, take a
longer time for a complete cycle.
In contrast, a stiffer spring (one with greater constant k) exerts a
greater force at a given deformation x, causing greater
acceleration, higher frequency, and a shorter time T per cycle.
• The period T and frequency f of SHM are completely determine by
m and k, it does not depend on the amplitude A.
• Large A means larger restoring forces, larger average speed to
compensate for having to travel a larger distance, so the same
total time is involved.
Example 13.2 angular frequency, frequency, and period in SHM
A spring is mounted horizontally, with its left end held stationary. By
attaching a spring balance to the free end and pulling toward the right,
we determine that the stretching force is proportional to the
displacement and that a force 6.0 N causes a displacement of 0.300 m.
We remove the spring balance and attach a 0.50 kg glider to the end,
pull it a distance of 0.020 m along a frictionless air track, release it, and
watch it oscillate.
a. Find the force constant of the
spring.
b. Find the angular frequency,
frequency, and period of the
oscillation
x versus t graph
SHM phase, position, velocity, and acceleration
• SHM can occur with
various phase angles.
• For a given phase we can examine
position, velocity, and acceleration.
Watch variables change for a glider example
• As the glider
undergoes SHM,
you can track
changes in velocity
and acceleration as
the position changes
between the classical
turning points.
Test Your Understanding 13.2
•
A glider is attached to a spring. If the glider is moved to x = 0.10 m
and released from rest at time t = 0, it will oscillate with amplitude
A = 0.10 m and phase angle Φ = 0.
1. Suppose instead that at t = 0 the glider is at x = 0.10 m and is
moving to the right. In this situation
a. Is the amplitude greater than, less than, or equal to 0.10 m?
b. Is the phase angle greater than, less than, or equal to zero?
2. Suppose instead that at t = 0 the glider is at x = 0.10 and is moving
to the left. In this situation
a. Is the amplitude greater than, less than, or equal to 0.10 m?
b. Is the phase angle greater than, less than, or equal to zero?
13.3 Energy in SHM
• The force exerted by an ideal spring is a conservative force, and the
vertical forces do no work, so the total mechanical energy of the
system of a body in SHM is conserved. (assume that the mass of the
spring itself is negligible.
1
1 2
2
E  mvx  kx  Constant
2
2
• When x = A (or –A), vx = 0. at this point the energy is entirely
potential, E = ½ kA2.
• Because E is constant, it is equal to ½ kA2 at any point
1
1 2 1 2
2
E  mvx  kx  kA
2
2
2
• Using this equation, we can solve for vx at any given point x if A
is known.
Interpreting E, K, and U in SHM
• Energy is conserved during SHM and the forms (potential and
kinetic) interconvert as the position of the object in motion
changes.
Example 13.4 Velocity, acceleration, and energy in SHM
In the oscillation described in Example 13.2, k = 200 N/m, m = 0.50
kg, and the oscillating mass released from rest at x = 0.020 m.
a. Find the maximum and minimum velocities attained by the
oscillating body.
b. Compute the maximum acceleration.
c. Determine the velocity and acceleration when the body has moved
halfway to the center from its original position.
d. Find the total energy, potential energy, and kinetic energy at this
position.
Example 13.5 Energy and momentum in SHM
A block with mass M attached to
a horizontal spring with force
constant k is moving with simple
harmonic motion having
amplitude A1. At the instant when
the block passes through its
equilibrium position, a lump of
putty with mass m is dropped
vertically onto the block from a
very small height and sticks to it.
a. Find the new amplitude and
period.
b. Repeat part (a) for the case in
which the putty is dropped on
the block when it is at one end
of its path.
Test Your Understanding 13.3
1. To double the total energy for a mass-spring
system oscillating in SHM, by what factor must
the amplitude increase?
a.
b.
c.
d.
4
2
21/2
21/4
2. By what factor will the frequency change due
to this amplitude increase?
a.
b.
c.
d.
e.
4
2
21/2
21/4
It does not change
13.4 Applications of Simple Harmonic Motion
SHM can occur in any system in which there is a restoring force
that is directly proportional to the displacement from equilibrium,
as given by: Fx = - kx
Vertical SHM
Vertical SHM doesn’t differ in any essential way from horizontal
SHM. The only real change is the equilibrium position.
The same ideas hold if a body with weight mg is placed atop a
compressible spring.
k

m
Example 13.6 Vertical SHM in an old car
The shock absorbers in an old car with mass 1000 kg are completely
worn-out. When a 980 N person climbs slowly into the car to its
center of gravity, the car sinks 2.8 cm. when the car, with the person
aboard, hits a bump, the car starts oscillating up and down in SHM.
Model the car and person as a single body on a single spring, and
find the period and frequency of the oscillation.
Angular SHM
• Watches keep time based on regular oscillations of a balance
wheel initially set in motion by a spring.
• The wheel has a moment of inertial I about its axis. A coil spring
exerts a restoring torque τz that is proportional to the angular
displacement θ from the equilibrium position.
τz = - ĸθ
(analog to Fx = -kx)
Where ĸ (kappa) is a constant called torsion constant
 z  I

   I

I
1
f 
2

  
I

I
T  2
I

• The motion of rotational SHM is described by the function:
θ = Θcos(ωt + Φ)
Test Your Understanding 13.4
•
1.
2.
3.
A block attached to a hanging ideal spring oscillates up and
down with a period of 10 s on earth. If you take the block
and spring to Mars. Where the acceleration due to gravity is
only about 40% as large as on earth, what will be the new
period of oscillation?
10 s
More than 10 s
Less than 10 s
13.5 The Simple Pendulum
A simple pendulum is an idealized model consisting of a point
mass suspended by a massless, unstretchable string. When the point
mass is pulled to one side of its straight-down equilibrium position
and released, it oscillates about the equilibrium position.
A person a swing can be modeled as simple pendulum
The restoring force is provided by
gravity;
F  mg sin 
If the θ is small, sinθ ≈ θ
F  mg
The motion is approximately
simple harmonic.
x
mg
F  mg  
x
L
L
x

L
F  ma

g
L
g
a x
L
L
T  2
g
graphs
Period vs. length
period
period
Period vs. length
Length (m)
length(m)
Example 13.8 A simple pendulum
Find the period and frequency of a simple pendulum 1.000 m long
at a location where g = 9.800 m/s2.
example
• A simple pendulum of length l, whose bob has mass
m, oscillates with a period T. If the bob is replaced by
one of mass 4m, what is the period of oscillation in
terms of T?
example
• A pendulum with a period of 1 s on Earth, where the
acceleration due to gravity is g, is taken to another
planet, where its period is 2 s. What is the acceleration
due to gravity on the other planet?
example
• A simple pendulum has a period of 2 s for small
amplitude oscillations. What is the length of the
pendulum?
Test Your Understanding 13.5
• When a body oscillating on a horizontal spring passes through
its equilibrium position, its acceleration is zero. When the bob
of an oscillating simple pendulum pass through its equilibrium
position, is its acceleration zero?
No, because there is a net force (centripetal force)
acting on the bob causing a change in direction of
motion.
Damped oscillations
•
A person may not wish
for the object they
study to remain in
SHM. Consider shock
absorbers and your
automobile. Without
damping the
oscillation, hitting a
pothole would set your
car into SHM on the
springs that support it.
13.6 The Physical Pendulum
• A physical pendulum is any real pendulum that uses an extended
body in motion.
When the body is displaced as shown,
the weight mg causes a restoring torque:
 z  (mg sin  )d
When θ is small, we can approximate that:
  sin 
 z  I
 (mgd )  I
mgd
 

I
 z  (mgd )
mgd

I
I
T  2
mgd
Example 13.9 Physical pendulum vs. simple pendulum
Suppose the body in the
figure is a uniform rod
with length L, pivoted at
one end. Find the period of
its motion.
Test Your Understanding 13.6
• The center of gravity of simple pendulum of mass m and
length L is located at the position of the pendulum bob, a
distance L from the pivot point. The center of gravity of a
uniform rod of the same mass m and length 2L pivoted at one
end is also a distance L from the pivot point. How does the
period of this uniform rod compare to the period of the simple
pendulum?
1. The rod has a longer period
2. The rod has a shorter period
3. The rod has the same period
I = 1/3 m(2L)2 = 4/3 mL2
d=L
T = 2π√4L/3g
Lab – determine spring constant K
• Purpose: Use SHM to determine spring constant k
• Material:
• (questions to ask your self: What data do you need to
determine k? How are you going to obtain your data?
How are you going to minimize experimental error?)
• Procedure: Briefly describe how the lab is going to be done.
Someone who was not present during the lab should be able to
understand how the experiment was perforem and be able to
reproduce the results by reading your procedure.
• Data table: record you data with units in the headings
• Data analysis: use your collected data to determine spring
constant.