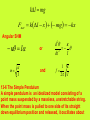* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 1-2 The Nature of Physics Physics is an experimental
Mass versus weight wikipedia , lookup
Old quantum theory wikipedia , lookup
Casimir effect wikipedia , lookup
Angular momentum wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Specific impulse wikipedia , lookup
Elementary particle wikipedia , lookup
Electromagnetism wikipedia , lookup
History of subatomic physics wikipedia , lookup
Conservation of energy wikipedia , lookup
Potential energy wikipedia , lookup
Coriolis force wikipedia , lookup
Negative mass wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Fundamental interaction wikipedia , lookup
Woodward effect wikipedia , lookup
Photon polarization wikipedia , lookup
Four-vector wikipedia , lookup
Time in physics wikipedia , lookup
Mechanics of planar particle motion wikipedia , lookup
Aristotelian physics wikipedia , lookup
Centrifugal force wikipedia , lookup
Speed of gravity wikipedia , lookup
Anti-gravity wikipedia , lookup
Lorentz force wikipedia , lookup
Jerk (physics) wikipedia , lookup
Classical mechanics wikipedia , lookup
Weightlessness wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Matter wave wikipedia , lookup
Equations of motion wikipedia , lookup
Newton's laws of motion wikipedia , lookup
西尔斯物理学 The Sears and Zemansky' s University Physics Units, Physical Quantities and Vectors •1-1 Introduction •For two reasons: •1. Physics is one of the most fundamental of the sciences. •2. Physics is also the foundation of all engineering and technology. •The But there' s another reason. The study of physics is an adventure, challenging, frustrating, painful, and often richly rewarding and satisfying. •The In this opening chapter, we' the ll go over •ll need throughout our study. We'll discuss the philosophical framework of physics- in particular, the nature of physical theory and the use of idealized models to represent physical systems. We'll introduce the systems of units used to describe physical quantities and discuss ways to describe the accuracy of a number. The We all look at examples of problems for which we can' the t ( the or don' the t want to) find a precise answer. Finally, we' ll study several aspects of vectors algebra. •1-2 The Nature of Physics Physics is an experimental science. Physicists observe the phenomena of nature and try to find patterns and principles that relate these phenomena. •These patterns are called physical theories or, when they are very well established and of broad use, physical laws or principles. The development of Physical theory requires creativity at every stage. The physicist has to learn to ask appropriate questions. 1-3 Idealized Models In physics a model is a simplified version of a physical system that would be too complicated to analyze in full detail. To make an idealized model of the system, we have to overlook quite a few minor effects to concentrate on the most important features of the system. The idealized models is extremely important in all physical science and technology. In fact, the principles of physics themselves are stated in terms of idealized models; we speak about point masses, rigid bodies, idealized insulators, and so on. 1-4 Standards and Units Physics is an experimental science. Experiments require measurements, and we usually use numbers to describe the results of measurements. 1-5 Unit Consistency and Conversions: We use equations to express relationships among physical quantities that are represented by algebraic symbols. Each algebraic symbol always denote both a number and a unit. An equation must always be dimensionally consistent. 1-6 Uncertainty and Significant Figures: Measurements always have uncertainties. If you measure the thickness of the cover of this book using an ordinary ruler, your measurement is reliable only to the nearest millimeter, and your result will be 3mm. It would be wrong to state this result as 3.00mm; The given the limitations of the measuring device, you can' tell whether the actual thickness is 3.00 mms,2.85 mms,3.11 mms of or. But if you use a micrometer caliper, a device that measures distances reliably to the nearest 0.01mm, the result will be 2.91mm. The distinction between these two measurements is in their uncertainty. The measurement using the micrometer caliper has a smaller uncertainty; It' s a more accurate measurement. The uncertainty is also called the error, because it indicates the maximum difference there is likely to be between the measured value and the true value. The uncertainty or error of a measured value depends on the measurement technique used. 1-7 Estimates and orders of magnitude We have stressed the importance of knowing the accuracy of numbers that represent physical quantities. But even a very crude estimate of a quantity often gives us useful information. Sometimes we know how to calculate a certain quantity but have to guess at the data we need for the calculation. Or the calculation might be too complicated to carry out exactly, so we make some rough approximations. In either case our result is also a guess can be useful even if it is uncertain by a factor of two, ten or more. Such calculations are often called order-ofmagnitude estimates. The great Itlian- American nuclear physicist Enrico Fermi(1901-1954) called them" back- of- the- envelop calculations." 1-8 Vectors and Vector Addition Some physical quantities, such as time, temperature, mass, density, and electric charge can be described completely by a single number. Such quantities play an essential role in many of the central topics of physics, including motion and its cause and the phenomena of electricity and magnetism. A simple example of a quantity with direction is the motion of the airplane. To describe this motion completely, we must say not only how fast the plane is moving, but also in what direction. Another example is force, which in physics means a push or pull exerted on a body. Giving a complete description of a force means describing both how hard the force pushes or pulls on the body and the direction of the push or pull. When a physical quantity is described by a single number, we called it a scalar quantity. In contrast, a vector quantity has both a magnitude( the " how much" or "how big" part) and a direction in space. Calculations with scalar quantities use the operations of ordinary arithmetic. To understand more about vectors and how they combine, we start with the simplest vector quantity, displacement. Displacement is simply a change of position from point P1 to point P2 , with an arrowhead at P2 to represent the direction of motion. Displacement is a vector quantity because we must state not only how far the particle moves, but also in what direction. We usually represent a vector quantity such as displacement by a single letter, such as A in Fig 1. P2 P2 P3 A A A P1 Fig 1 P1 Fig 2 B Fig 3 When drawing any vector, we always draw a line with an arrowhead at its tip. The length of the line shows the vector' s magnitude, and the direction of the line shows the vector' s direction. Displacement is always a straight-line segment, directed from the starting point to the end point, even though the actual path of the particle may be curved. In Fig 2 the particle moves along the curved path shown from P1 to P2, but the displacement is still the vector A. Note that displacement is not related directly to the total distance traveled. If the particle were to continue on to P3 and then return to P1, the displacement for the entire trip would be zero. If two vectors have the same direction, they are parallel. If they have the same magnitude and the same direction, they are equal. The vector B in Fig 3, however, is not equal to A because its direction is opposite to that of A. We define the negative of a vector as a vector having the same magnitude as the original vector but the opposite direction. The negative of vector quantity A is denoted as – A, and we use a boldface minus sign to emphasize the vector nature of the quantities. Between A and B of Fig. 3 may be written as A = -B or B = -A. When two vectors A and B have opposite directions, whether their magnitudes are the same or not, we say that they are anti-parallel. We usually represent the magnitude of a vector quantity (its length in the case of a displacement vector) by the same letter used for the vector, but in light italic type with no arrow on the top, rather than bold-face italic with an arrow (which is reserved for vectors). An alternative notation is the vector symbol with vertical bars on both sides. Vector Addition Now suppose a particle undergoes a displacement A, followed by a second displacement B. The final result is the same as if the particle had started at the same initial point and undergone a single A A displacement C, as shown. We call displacement C the vector sum, or resultant, of displacements A and B. We express this relationship symbolically as C A B Y B C C A A Ay B Fig 4 A O Fig 5 Ax X Fig 6 If we make the displacements A and B in reverse order, with B first and A second, the result is the same (Fig.4). The final result is the same as if the particle had started at the same initial point and undergone a single displacement C, as shown. We call displacement C the vector sum, or resultant, of displacement A and B. We express this relationship symbolical as C = A + B. If we make the displacements A and B in reverse order, with B first and A second, the result is the same. Thus C = B + A and A + B = B + A 1-9 Components of Vectors To define what we mean by the components of a vector, we begin with a rectangular (Cartesian) coordinate system of axes. The We then draw the vector we' the re considering with its tail at O, the origin of the coordinate system. We can represent any vector lying in the xy-plane as the sum of a vector parallel to the x-axis and a vector parallel to the y-axis. These two vectors are labeled Ax and AY in the figure; they are called the component vectors of vector A, and their vector sum is equal to A. In symbols, A = Ax + Ay. (1) By definition, each component vector lies along a coordinate-axis direction. Thus we need only a single number to describe each one. When the component vector Ax points in the positive x-direction, we define the number Ax to be equal to the magnitude of Ax. When the component vector Ax points in the negative x-direction, we define the number Ax to be equal to the negative of that magnitude, keeping in mind that the magnitude of two numbers Ax and Ay are called the components of A. The components Ax and Ay of a vector A are just numbers; they are not vectors themselves. Using components We can describe a vector completely by giving either its magnitude and direction or its x- and y- components. Equations (1) show how to find the components if we know the magnitude and direction. We can also reverse the process; we can find the magnitude and direction if we know the components. We find that the magnitude of a vector A is A Ax2 Ay2 (2) where we always take the positive root. Equation (2) is valid for any choice of x-axis and y-axis, as long as they are mutually perpendicular. The expression for the vector direction comes from the definition of the tangent of an angle. If is measured from the positive x-axis, and a positive angle is measured toward the positive yaxis (as in Fig. 6) then tan A y A arctan A A x y and We will always use the notation arctan for the inverse tangent function. x 1-10 Unit Vectors A unit vector is a vector that has a magnitude of 1. Its only purpose is to point, that is, to describe a direction in space. Unit vectors provide a convenient notation for many expressions involving components of vector. In an x-y coordinate system we can define a unit vector i that points in the direction of the positive x-axis and a unit vector j that points in the direction of the positive y-axis. Then we can express the relationship between component vectors and components, described at the beginning of section 1-9, as follows Ax = Ax i , Ay = Ay j ; A = Ax i+ Ay j . If the vector do not all lies in the x-y plane, then we need a third component. We duce a third unit vector k that points in the direction of the positive z-axis. The generalized forms of equation is A = Ax i + Ay j + Az k 1-11 Products of vectors We have seen how addition of vectors develops naturally from the problem of combining displacements, and we will use vector addition for many other vector quantities later. We can also express many physical relationships concisely by using products of vectors. Vectors are not ordinary numbers, so ordinary multiplication is not directly applicable to vectors. We will define two different kinds of products of vectors. Scalar product: The scalar product of two vectors A and B is denoted by A · B. Because of this notation, the scalar product is also called the dot product. We define A ? B to be the magnitude of A multiplied by the component of B parallel to A. Expressed as an equation: A B AB cos A B cos The scalar product is a scalar quantity, not a vector, and it may be positive, negative, or zero. When Φ is between 0° and 90 °, the scalar product is positive. When is between 90° and 180° , it is negative. Vector product : The vector product of two vectors A and B, also called the cross product, is denoted by AB. To define the vector product AB of two vectors A and B, we again draw the two vectors with their tail at the same point( Fig.1-20a). The two vectors then lie in a plane. We define the vector product to be a vector quantity with a direction perpendicular to this plane (that is, perpendicular to both A and B) and a magnitude equal to AB sin. That is, if C = AB, then C = AB sin. We measure the angle from A toward B and take it to be the smaller of the two possible angles, so ranges from 0 °to 180. There are always two directions perpendicular to a given plane, one on each side of the plane. We choose which of these is the direction of AB as follows. Imagine rotating vector A about the perpendicular line until it is aligned with B, choosing the smaller of the two possible angles between A and B. Curl the fingers of your right hand around the perpendicular line so that the fingertips point in the direction of rotation; your thumb will then point in the direction of AB. This right-hand rule is shown in Fig. 1-20a. The direction of the vector product is also the direction in which a right-hand screw advances if turned from A toward B. 2 Motion Along a Straight Line 2-1 Introduction In this chapter we will study the simplest kind of motion: a single particle moving along a straight line. We will often use a particle as a model for a moving along body when effects such as rotation or change of shape are not important. To describe the motion of a particle, we will introduce the physical quantities velocity and acceleration. 2-2 Displacement, Time, And Average Velocity Lets generalize the concept of average velocity. At time t1 the dragster is at point P1 with coordinate x1, and at time t2 it is at point P2, with coordinate x2. The displacement of the dragster during the time interval from t1 to t2 is the vector from P1 to P2, the with x- component( the x2 – x1) and with y- and zcomponents equal to zero. The The x- component of the dragster' the s displacement is just the change in the coordinate x, which we write more compact way as x x2 x1 (2-1). Be sure you understand that x is not the product of and x; The it is a single symbol that means" the change in the quantity x. ” We likewise write the time interval from t1 to t2 as t t2 t1 .Note that x or t always means the final value minus the initial value, never the reverse. We can now define the x-component of average velocity more precisely: it is the x- component of displacement, x , divided by the time interval t during which the displacement occurs. The We represent this quantity by the letter v with a subscript" av" to signify average value: x x x (2-2) v t t t For the example we had x1 = 19m, x2 = 277m, t1 = 1.0s and t2 = 4.0s so Eq.(22) gives 277m 19m 258m v 86m / s 4.0m 1.0m 3.0s The average velocity of the dragster is positive. This means that during the time interval, the coordinate x increased and the dragster moved in the positive x- direction. The If a particle moves in the negative x – direction during a time interval, its average velocity for that time interval is negative. 2-3 Instantaneous Velocity The average velocity of a particle during a time interval cannot tell us how fast, or in what direction, the particle was moving at any given time during the interval. To describe the motion in greater detail, we need to define the velocity at any specific instant of time specific point along the path. 2 1 av 2 av 1 Such a velocity is called instantaneous velocity, and it needs to be defined carefully. To find the instantaneous velocity of the dragster in Fig. 2-1 at the point P1, we imagine moving the second point P2 closer and closer to the first point P1. We compute the average velocity vav = x / t over these shorter and shorter displacements and time intervals. Both x and t become very small, but their ratio does not necessarily become small. In the language of calculus the limit of x /t as t approaches zero is called the derivative of x with respect to t and is written dx/dt. The instantaneous velocity is the limit of the average velocity as the time interval approaches zero; it equals the instantaneous rate of change of position with time. We use the symbol v, with no subscript, for instantaneous velocity: x (straight-line motion) (2-3). v lim t We always assume that the time interval ?t is positive so that v has the same algebraic sign as ?x. If the positive x-axis points to the right, as in Fig. 2-1, a positive value of mean that x is increasing and motion is toward the right; a negative value of v means that x is decreasing and the motion is toward the left. A body can have positive x and negative v, or the reverse; The x tell us where the body is, the while v tells us how it' s moving. t 0 Instantaneous velocity, like average velocity, is a vector quantity. Equation (2-3) define its x-component, which can be positive or negative. In straight-line motion, all other components of instantaneous velocity are zero, and in this case we will often call v simply the instantaneous velocity. The The terms" velocity" and" speed" are used the interchangeably in everyday language, but they have distinct definitions in physics. We use the term speed to denote distance traveled divided by time, on ether an average or an instantaneous basis. Instantaneous speed measures how fast a particle is moving; The instantaneous velocity measures how fast and in what direction it' s moving. For example, a particle with instantaneous velocity v = 25m/s and a second particle with v = - 25m/s are moving in opposite direction the same instantaneous speed of 25m/s. Instantaneous speed is the magnitude of instantaneous velocity, and so instantaneous speed can never be negative. Average speed, however, is not the magnitude of average velocity. Example: The A cheetah is crouched in ambush 20 m to the east of an observer' s blind. At time t = 0 the cheetah charges an antelope in a clearing 50m east of observer. The cheetah runs along a straight line. Later analysis of a videotape shows that during the first 2.0s of the attack, The the cheetah' the s coordinate x varies with time according to the equation x=20 ms+(5.0 ms/ s2) t2. (Note that the units for the numbers 20 and 5.0 must be as shown to make the expression dimensionally consistent.) Find(a) the displacement of the cheetah during the interval between t1 = 1.0s and t2 = 2.0s.(b) Find the average velocity during the same time interval. (c) Find the instantaneous velocity at time t1 = 1.0s by taking ?t = 0.1s, then t = 0.01s, then t = 0.001s. (d) derive a general expression for the instantaneous velocity as a function of time, and from it find v at t = 1.0s and t = 2.0s Solution: (a) The At time t1= the 1.0 s the cheetah' the s position x1 is x1=20 ms+(5.0 ms/ s2)(1.0 ses)2=25 ms. At time t2 = 2.0s its position x2 is x2 = 20m + (5.0m/s2)(2.0s)2 = 40m. The displacement during this the interval is the x= x2 – x1= 40 m – 25 m=15 m. (b) The average velocity during this time interval is x x 40m 25m 15m v 15m / s t t 2.0s 1.0s 1.0s At time t2, the position is x2 = 20m+(5.0m/s2)(1.1s)2 = 26.05m 2 1 av 2 1 The average velocity during this interval is v av 26.05m 25 10.5m / s 1.1s 1.0s We invite you to follow this same pattern to work out the average velocities for the 0.01s and 0.001s intervals. The results are 10.05m/s and 10.005m/s. As t gets closer to 10.0m/s, so we conclude that the instantaneous velocity at time t = 1.0s is 10.0m/s. (d) We find the instantaneous velocity as a function of time by taking the derivative of the expression for x with respect to t. For any n the derivative of t is ntn-1, so the derivative of t2 is 2t. Therefore dx v 5.0m / s dt 2 2t 10tm / s At time t = 1.0s, v = 10m/s as we found in 2 part ( c ). At time t = 2.0s, v = 20m/s. 2-4 Average and Instantaneous Acceleration When the velocity of a moving body changes with time, we say that the body has an acceleration. Just as velocity describes the rate of change of position with time, acceleration describes the rate of change of velocity with time. Like velocity, acceleration is a vector quantity. In straight-line Motion its only nonzero component is along the axis along which the motion takes place. Average Acceleration Let' s consider again the motion of a particle along the x- axis. Suppose that at time t1 the particle is at point P1 and has x-component of (instantaneous) velocity v1, and at a later time t2 it is at point P2 and x-component of velocity v2. So the x-component of velocity changes by an amount v= v2 – v1 during the time interval t= t2 – t1. We define the average acceleration aav of the particle as it moves from P1 to P2 to be a vector quantity whose x-component is v, the change in the xcomponent of velocity, divided by the time interval t: v v v a t t t (average acceleration, straight-line motion) (2-4) For straight-line motion we well usually call aav simply the average acceleration, remembering that in fact it is the x-component of the average acceleration vector. If we express velocity in meters per second and time in seconds, then average acceleration is in meters per second per second. The This is usually written as m/ s2 and is read" meters per second squared." 2 1 av 2 1 Instantaneous Acceleration We can now define instantaneous acceleration, following the same procedure that we used to define instantaneous velocity. Consider this situation: A race car driver has just entered the final straightaway at the Grand Prix. He reaches point P1 at time t1, moving with velocity v1. He passes point P2, closer to the line, at time t2 with velocity v2.(Fig. 2-8) To define the instantaneous acceleration at point P1, we take the second point P2 in Fig. 2-8 to be closer and closer to the first point P1 so that the average acceleration is computed over shorter and shorter time intervals. The instantaneous acceleration is the limit of the average acceleration as the time interval approaches zero. In the language of calculus, instantaneous acceleration equals the instan-taneous rate of change of velocity with time. Thus a lim t 0 v dv (instantaneous acceleration, straight-line motion) (2-5) t dt Note that Eq. (2-5) is really the definition of the x-component of the acceleration vector; in straight-line motion, all other components of this vector are zero. Instantaneous acceleration plays an essential role in the laws of mechanics. The From now on, the when we use the term" acceleration", the we will always mean instantaneous acceleration, not average acceleration. Example: Average and instantaneous accelerations Suppose the velocity v of the car in Fig. 2-8 at any time t is given by the equation v = 60 m/s + (0.50 m/s3) t2. (a) Find the change in velocity of the car in the time interval between t1 = 1.0s and t2 = 3.0s. (b) Find the instantaneous acceleration in this time interval. (c) Find the instantaneous acceleration at time t1 = 1.0s by taking t to be first 0.1s, then 0.01s, then 0.001s. (d) Derive an expression for the instantaneous acceleration at any time, and use it to find the acceleration at t = 1.0s and t = 3.0s. Solution: (a) We first find the velocity at each time by substituting each value of t into the equation. At time t1 = 1.0s, v1 = 60m/s +(0.50m/s3)(1.0s)2 = 60.5m/s. At time t2 = 3.0s, v2 = 60m/s + (0.5m/s3)(3.0s)2 = 64.5m/s. The change in velocity v= v2 – v1=64.560.5=4.0 ms/ ses of –s. The time interval is t= 3.0 s – 1.0 s=2.0 s. (b) The average acceleration during this time interval is v v 4.0m / s a 2.0m / s t t 2.0s During the time interval from t1 = 1.0s to t2 = 3.0s, the velocity and average acceleration have the same algebraic sign (in this case, positive), and the car speeds up. 2 1 av 2 1 (c) When ?t = 0.1s, t2 = 1.1s and v2 = 60m/s + (0.50m/s3)(1.1s)2 = 60.605 m/s, v = 0.105m/s, a av v 0.105m / s 1.05m / s t 0.1s 2 We invite you repeat this pattern for t = 0.01s and t = 0.001s; the results are aav = 1.0005m/s2 respectively. As t gets smaller, the average acceleration gets closer to 1.0m/s2. We conclude that the instantaneous acceleration at t1 = 1.0s is 1.0m/s2. (d) The instantaneous acceleration is a = dv/dt, the derivative of a constant is zero, and the derivative of t2 is 2t . Using these, we obtain dv d 60m / s 0.50m / s t a dt dt 0.50m / s 2t 1.0m / s t. 3 3 3 When t = 3.0s, a = (1.0m/s3)(3.0s) = 1.0m/s2 2 2-5 Motion with Constant Acceleration The simplest acceleration motion is straight-line motion with constant acceleration. In this case the velocity changes at the same rate throughout the motion. This is a very special situation, yet one that occurs often in nature. As we will discuss in the next section, a falling body has a constant acceleration if the effects of the air are not important. The same is true for a body sliding on an incline or along a rough horizontal surface. Straight-line motion with nearly constant acceleration also occurs in technology, such as a jet-fighter being catapulted from the deck of an aircraft carrier. The In this section we' ll derive key equations for straight- line motion with constant acceleration. a t=0 v O a v t=t a O t=2t v a v a O at a t=3t v v0 O a t=4t O t t O v O Fig. 2-12 v v0 Fig. 2-13 Fig. 2-14 t t Figure 2-12 is a motion diagram showing the position, velocity, and acceleration at five different times for a particle moving with constant acceleration. Figure 213 and 2-14 depict this same motion in the from of graphs. Since the acceleration a is constant, the a-t graph (graph of acceleration versus time) in Fig. 2-13 is a horizontal line. The graph of velocity versus time has a constant slope because the acceleration is constant, and so the v-t graph is a straight line ( Fig. 2-14). The When the acceleration is constant, it' s easy to derive equations for position x and velocity v as functions of time. Let' s start with velocity. In Eq. (24) we can replace the average acceleration aav by the constant (instantaneous) acceleration a. We then have v v a 2 1 t 2 t1 (2-7) Now we let t1 = 0 and let t2 be any arbitrary later time t. We use the symbol v0 for the velocity at the initial time t is v. Then Eq. (2-7) because (2-8) v v0 a t 0 v v0 at Next we want to derive an equation for the position x of a particle moving with constant acceleration. To do this, we make use of two different expressions for the average velocity vav during the interval from t = o to any later time t. The first expression comes from the definition of vav Eq. (2-2), which holds true whether or not the acceleration is constant. We call the position at time t = 0 the initial position, denoted by x0. The position at the later time t is simply x. Thus for the time interval t = t – 0 and the corresponding displacement X= x – x0, Eq. (2-2) gives vav x x0 t (2-9) We can also get a second expression for vav that is valid only when the acceleration is constant, so that the v-t graph is a straight line (as in Fig. 2-14) and the velocity changes at a constant rate. vav v0 v (2-10)(constant acceleration only). Substituting that expression 2 for v into Eq. (2-10), we find 1 v0 v0 at 2 1 v0 at 2 vav (2-11) (constant acceleration only) Finally, we equate Eqs. (2-9) and (2-11) and simplify the result: x x0 1 vav at 2 t or 1 2 x x0 v0t at (2-12) 2 We can check whether Eqs.(2-8) and (2-12) are consistent with the assumption of constant acceleration by taking the derivative of Eq. (2-12). We find dx v v0 at dt which is Eq. (2-8). Differentiating again, we find simply as we should expect. dv a dt The In many problems, it' the s useful to have a relationship between position, velocity, and acceleration that does not involve the time. To obtain this, we first solve Eq. (2-8) for t, then substitute the resulting expression into Eq. (2-12) and simplify: 2 We transfer the term v v0 v v0 1 v v0 x0 x x0 v0 t a a 2 a a to the left side and multiply through by 2a: 2a x x0 2vv0 2v0 2 v 2 2v0 v v0 2 Finally, simplifying gives us. We can get one more useful relationship by equating the two expressions for vav, Eqs. (2-9) and (2-10), and v 2 v0 2 2a x x0 multiplying through by t. Doing this, we obtain v0 v (2-14) x x0 t 2 A special case of motion with constant acceleration occurs when the acceleration is zero. The velocity is then constant, and the equations of motion become simply v = v0 = constant, x = x0 + vt. 2-7 Velocity and Position by Integration This optional section is intended for students who have already learned a little integral calculus. In Section 2-5 we analyzed the special case of straight-line motion with constant acceleration. When a is not constant, as is frequently the case, the equations that we derived in that section are no longer valid. But even when a varies with time, we can still use the relation v = dx/dt to find the velocity v as a function of time if the position x is a known function of time. And we can still use a = dv/dt to find the acceleration a as a function of time if the velocity v is a known function of time. In many physical situations, however, position and velocity are not known as functions of time, while the acceleration is. aav Figure 2-13 O t1 t2 t We first consider a graphical approach, Figure 2-23 is a graph of acceleration versus time for a body whose acceleration is not constant but increases with time. We can divide the time interval between times t1 and t2 into many smaller intervals, calling a typical one t. Let the average acceleration during t be aav. From Eq. (2-4) the change in velocity v during t is v = aav t. Graphically, v equals the area of the shaded strip with height aav and width t, that is, the area under the curve between the left and right sides of t. The total velocity change during any interval (say, t1 to t2) is the sum of the velocity changes v in the small subintervals. So the total velocity changes is represented graphically by the total area under the a-t curve between the vertical lines t1 and t2. In the limit that all the T' the s become very small and their number very large, the the value of aav for the interval from any time t to t+ t approaches the instantaneous acceleration a at time t. In this limit, the area under the a-t curve is the integral of a (which is in general a function of t) from t1 to t2. If v1 is the velocity of the body at time t1 and v2 is the velocity at time t2, then The change in velocity v is the integral of acceleration a with respect to time. v v dv adt We can carry exactly the same procedure with the curve of velocity versus time where v is in general a function of t. If x1 is a body' s position at time t1 and x2 is its position at time t2, from Eq. (2-2) the displacement x during a small time interval ?t is equal to vav t, where vav is given by x x dx vdt (2-16) . The change in position x – that is, the displacement – is the time integral of velocity v. Graphically, the displacement between times t1 and t2 is the area under the v-t curve between those two times. If t1 = 0 and t2 is any later time t, and if x0 and v0 are the position and velocity, respectively, at time t = 0, then we can rewrite Eqs. (2-15) and (2-16) as follows: x x vdt (2-18). Here x and v are the position v v adt (2-17) and velocity at time t. If we know the acceleration a as a function of time and we know the initial velocity v0, we can use Eq, (2-17) to find the velocity v at any time; in other words, we can find v as a function of time. Once we know this function, and given the initial position x0, we can use Eq. (2-18) to find the position x at any time. Example 2-9 Sally is driving along a straight highway in her classic 1965 Mustang. At time t = 0, when Sally is moving at 10 m/s in the position x-direction, she passes a signpost at x = 50m. Her acceleration is a function of time: A= the 2.0 ms/ s2 – 1 2 1 v2 t2 v1 t1 2 x1 v1 x2 v2 t t 0 0 0 3 0 (a) Derive expressions for her velocity and position as functions of time.(b) At what time is her velocity greatest? (c) What is the maximum velocity? (d) Where is the car when it reaches maximum velocity. Solution: (a) The At time t=0, Sally' the s position is x0=50 ms, the and her velocity is v0=10 ms/ s. Since we are given the acceleration a as a function of time, we first use Eq. (2-17) to find the velocity v as a function of time t. v 10m / s 2.0m / s 0.10m / s t dt 1 10m / s 2.0m / s t 0.10m / s t 2 t 2 3 0 2 3 2 Then we use Eq.(2-18) to find x as a function of t: 1 x 50m 10m / s (2.0m / s )t 0.10m / s t dt 2 1 1 50m 10m / s t 2.0m / s t 0.10m / s t 2 6 At this instant, dv/dt = a = 0. Setting the expression for acceleration equal to zero, we obtain: 2.0m / s 0 2.0m / s 0.10m / s t t 20s 0 . 10 m / s ?$ t 2 3 2 0 2 2 3 2 2 3 3 3 (c) We find the maximum velocity by substituting t = 20s (when velocity is maximum) into the general velocity equation: 1 vmax 10 m / s 2.0m / s 20 s 2.0m / s 2 20 s 3 30 m 2 2 (d) The maximum value of v occurs at t = 20s, we obtain the position of the car (that is, the value of x) at that time by substituting t = 20s into the general expression for x: 1 1 x 50m 10m / s 20s 2.0m / s 20s 0.10m / s 20 517m 2 2 2 3 3 6 As before, we are concerned with describing motion, not with analyzing its causes. But the language you learn here will be an essential tool in later chapters when you use Newton' s laws of motion to study the relation between force and motion. Y r O X Z Figure 3-1 3-2 Position and velocity vectors To describe the motion of a particle in space, we first need to be able to describe the position of the particle. Consider a particle that is at a point P at a certain instant. The position vector r of the particle at this instant is a vector that goes from the origin of the coordinate system to the point P(Fig. 3-1). The figure also shows that the Cartesian coordinates x, y, and z of point P are the x-, y-, and z-components of vector r. Using the unit vectors introduced in Section 1-10, we can write r xi yj zk We can also get this result by taking the derivative of Eq(3-1). The unit vectors i, j and k are constant in magnitude and direction, so their derivatives are zero, and we find . This shows again that the components of dr dx dy dz v dt dt i dt j dt k v are dx/dt, dy/dt, and dz/dt. The magnitude of the instantaneous velocity vector v- that is, the speed – is given in terms of the components vx, vy, and vz by the Pythagorean relation: 2 2 2 v v vx v y vz The instantaneous velocity vector is usually more interesting and useful than the average velocity vector. From now on, when we use the word" velocity", we will always mean the instantaneous velocity vector v( the rather than the average velocity vector). Usually, we won' even bother to call v a vector. v1 v 3-3 The Acceleration Vector v2 In Fig (3-1), a particle is moving along a curved The vectors v1 and v2 represent the particle' s instantaneous velocities at time t1, when the particle is at point P1, and time t2, When the particle is at point P2. The two velocities may differ in both magnitude and direction. We define the average acceleration aav of the particle as the particle as it moves from P1 and P2 as the vector change in velocity, v2-v1= v, divided by the time interval t2-t1 = t: v2 v1 v aav t2 t1 t Average acceleration is a vector quantity in the same direction as the vector v. As in Chapter 2, we define the instantaneous acceleration a at point P1as the limit approached by the average acceleration when point P2 approaches point P1 and v and t both approach zero; the instantaneous acceleration is also equal to the instantaneous rate of change of velocity with time. Because we are not restricted to straight-line motion, instantaneous acceleration is now a vector: v 1 v dv a lim t 0 t dt v2 v P2 v1 P1 v1 P1 A a v2 aav B C The velocity vector v, as we have seen, is tangent to the path of the particle. But the construction in fig.C shows that the instantaneous acceleration vector a of a moving particle always points toward the concave side of a curved paththat is, toward the inside of any turn that the particle is making. We can also see that when a particle is moving in a curved path, it always has nonzero acceleration. We will usually be interested in the instantaneous acceleration, not the average acceleration. From now on, we will use the term “acceleration” to mean the instantaneous acceleration vector a. Each component of the acceleration vector is the derivative of the corresponding component of velocity: dvx dvy dvz dv dv a i j k z y dvx a a x ax dt dt dt y dt dt dt Also, because each component of velocity is the derivative of the corresponding coordinate, we can express the ax, ay and az of the acceleration vector a as 2 2 2 2 2 2 d y d z d x d y d z d x ay 2 az 2 a 2 i 2 j 2 k ax 2 dt dt dt dt dt dt Example: Calculating average and instantaneous acceleration; Let’s look again at the radio-controlled model car in Example 3-1. We found that the components of instantaneous velocity at any time t are dx vx 0.25 m 2 2t s dt dy vy 1.0 m 2 0.025 m 3 3t 2 s s dt and that the velocity vector is s m m t j 1.0 0.075 s s v vx i v y j 0.50 m 2 ti 2 2 a) Find the components of the average acceleration in the interval from t=0.0s to t=2.0s. b) Find the instantaneous acceleration at t=2.0s. Solution a) From Eq. (3-8), in order to calculate the components of the average acceleration, we need the instantaneous velocity at the beginning and the end of the time interval. We find the components of instantaneous velocity at time t=0.0s by substituting this value into the above expressions for vx, and vy. We find that at time t = 0.0s, vx = 0.0m/s, vy = 1.0m/s . We found in Example 3-1 that at t = 2.0s the values of these components are vx = -1.0m/s, vy = 1.3m/s. Thus the components of average acceleration in this interval are aav y v y 1.3 m s 1.0 m s 0.15 m 2 s t 2.0s 0.0s a 0.5 m i 0.30 m j s s 2 2 b) From Eq. 3-10 the components acceleration vector a as m m vx 1.0 s 0.0 s aav x 0.5 m 2 s t 2.0s 0.0s At time t = 2.0s, the components of instantaneous acceleration are ax = -0.5m/s2 , ay = (0.15m/s3)(2.0s) = 0.30m/s2 . The acceleration vector at this time is m m a a x i a y j 0.50 2 i 0.15 2 j s s v2 P1 P2 v1 v s P1 R A P2 v1 O O v2 B 3-5 Motion in A Circle When a particle moves along a curved path, the direction of its velocity changes.As we saw in Section 3-3, this means that the particle must have a component of acceleration perpendicular to the path, even if its speed is constant. In this section we’ll calculate the acceleration for the important special case of motion in a circle. Uniform Circular Motion When a particle moves in a circle with constant speed, the motion is called uniform circular motion. There is no component of acceleration parallel (tangent) to the path; otherwise, the speed would change. The component of acceleration perpendicular (normal) to the path, which cause the direction of the velocity to change, is related in a simple way to the speed of the particle and the radius of the circle. In uniform circular motion the acceleration is perpendicular to the velocity at each instant; as the direction of the velocity changes, the direction of the acceleration also changes. Figure A shows a particle moving with constant speed in a circular path radius R with center at O. The particle moves from P1 to P2 in a time t. The vector change in velocity v during this time is shown in Fig. B. The angles labeled in Fig. A and B are the same because v1 is perpendicular to the line OP1 and v2 is perpendicular to the line OP2. Hence the triangles OP1P2(Fig. A) and OP1P2(Fig. B) are similar. Ratios of corresponding sides are equal, so or v1 v s v s R t R The magnitude aav of the average acceleration during t is therefore v v1 s aav t R t The magnitude of the instantaneous acceleration a at point P1. Also, P1 can is the limit of this expression as we take point P2 closer and closer to point P1: v s v1 s a lim 1 lim t 0 R t R t 0 t But the limit of s/ t is the speed v1 at point P1. Also, P1 can be any point on the path, so we can drop the subscript and let v represent the speed at any point. Then v2 arad R Because the speed is constant, the acceleration is always perpendicular to the instantaneous velocity.We conclude: In uniform circular motion, the magnitude a of the instantaneous acceleration is equal to the square v divided by the radius R of the circle. Its direction is perpendicular to v and inward along the radius. Because the acceleration is always directed toward the center of the circle, it is sometimes called centripetal acceleration. Non-Uniform Circular Motion We have assumed calculate throughout this section that the particle’s speed is constant. If the speed varies, we call the motion non-uniform circular motion. In non-uniform circular motion, still gives the radial component of acceleration arad v2 R , which is always perpendicular to the instantaneous velocity and direction toward the center of the circle. But since the speed v has different values at different points in the motion, the value of a rad is not constant. In non-uniform circular motion there is also a component of acceleration that is parallel to the instantaneous velocity. This is the component a11 that we discussed in Section 3-3; here we call this component atan to emphasize that it is tangent to the circle. From the discussion at the end of Section 3-3 we see that the tangential component of acceleration atan is equal to the rate of change of speed. Thus 2 d v v atan and arad dt R The vector acceleration of a particle moving in a circle with varying speed is the vector sum of the radial and tangential components of accelerations. The tangential component is in the same direction as the velocity if the particle is speeding up, and is in the opposite direction if the particle is slowing down. In uniform circular motion there is no tangential component of acceleration, but the radial component is the magnitude of dv/dt. We have mentioned before that the two quantities |dv/dt| and d|v|/dt are in general not equal. In uniform circular motion the first is constant and equal to v2/R; the second is zero. 4 Newton’s Laws of Motion 4-1 Introduction In this chapter we will use the kinematic quantities displacement, velocity, and acceleration along with two new concepts, force and mass, to analyze the principles of dynamics. These principles can be wrapped up in a neat package of three statements called Newton’s laws of motion. The first law states that when the net force on a body is zero, its motion doesn’t change. The second law relates force to acceleration when the net forces is not zero. The third law is a relation between the forces that two interacting bodies exert on each other. These laws, based on experimental studies of moving bodies, are fundamental in two ways. First, they cannot be deduced or proved from other principles. Second, they are the foundation of classical mechanics ( also called Newtonian mechanics). Newton’s laws are not universal, however; they require modification at very high speeds (near the speed of light) and for very small size ( such as within the atom). 4-2 Force And Interactions In everyday language, a force is a push or pull. The concept of force gives us a quantitative description between two bodies or between a body and its environment. When a force involves direct contact between two bodies, we call it a contact force. Contact forces include the pushes or pulls you exert with your hand, the force of rope pulling on a block to which it is tied, and the friction force that the ground exerts on a ball player sliding into home. There are also forces, called longrange forces, that act even when the bodies are separated by empty space. You’ve experienced long-range forces if you’ve ever played with a pair of magnets. Gravity, too, is a long-range force; the sun exerts a gravitational pull on the earth, even over a distance of 150 million kilometers, that keeps the earth in orbit. Force is a vector quantity; you can push or pull a body in different directions. Thus to describe a force, we need to describe the direction in which it acts as well as its magnitude, the quantity that describes “how much” or “how hard” the force pushes or pulls. When two forces F1 and F2 act at the same time at point A of a body (Fig. 4-2), experiment shows that the effect on the body’s motion is the same as the effect of a single force R equal to the vector sum of the original forces: R = F1 + F2. F2 Fy F R A O F1 Fx Fig.4-2 Fig. 4-3 More generally, the effect of any number of forces applied at a point on a body is the same as the effect of a single force equal to the vector sum of the forces. This important principle goes by the superposition of forces. The experimental discovery that forces combine according to vector addition is of the utmost importance. We will use this fact many times throughout our study of physics . It allows us to replace a force by its component vectors, as we did with displacements in Section 1-9. For example, in Fig. 4-3, force F acts on a body at point O. The component vectors of F in the directions OX and OY are Fx and Fy. When Fx and Fy are applied simultaneously, the effect is exactly the same as the effect of the original force F. Any force can be replaced by its component vectors, acting at the same point. 4-3 Newton’s First Law A body acted on by no net force moves with constant velocity (which may be zero) and zero acceleration. This is Newton’s first law of motion. It’s important to note that the net force is what matters in Newton’s first law. For example, a physics book at rest on a horizontal table top has two forces acting on it; the downward force of the earth’s gravitational attraction ( a long-range force that acts even if the table top is elevated above the ground) and an upward supporting force exerted by the table top ( a contact force). The upward push of the surface is just as great as the downward pull of gravity, so the net force acting on the book (that is, the vector sum of the two forces) is zero. In agreement with Newton’s first law, if the book is at rest on the table top, it remains at rest. We find that if the body is at rest at the start, it remains at rest; if it is initially moving, it continues to move in the same direction with constant speed. These results show that in Newton’s first law, zero net force is equivalent to no force at all. This is just the principle of superposition of forces that we saw in Section 4-2. 4-4 Newton’s Second Law Mass and Force Mass is a quantitative measure of inertia, which we discussed in Section 4-3. The greater its mass, the more a body “resists” being accelerated. The SI unit of mass is kilogram. One Newton is the amount of net force that gives an acceleration of one meter per second squared to a body with a mass of one kilogram. We can use this definition to calibrate the spring balances and other instruments used to measure forces. Because of the way we have defined the newton, it is related to the units of mass, length, and time. For Eq. F ma (45) to be dimensionally consistent, it must be true that 1newton = (1 kilogram) (1 meter per second squared). We can also use Eq. (4-5) to compare a mass with the standard mass and thus to measure masses. Suppose we apply a constant net force F to a body having a known mass m1 and we find an acceleration of magnitude a1. We then apply the same force to another body having an unknown mass m2, and we find an acceleration of magnitude a2. Then, according to Eq. (4-5) m2 a1 m1 a2 m1a1 m2 a2 (4-6) The ratio of the masses is the inverse of the ratio of the accelerations. Figure 412 shows the inverse proportionally between mass and acceleration. In principle we could use Eq. (4-6) to measure an unknown mass m2, but it is usually easier to determine mass indirectly by measuring the body’s weight. When two bodies with masses m1 and m2 are fastened together, we find that the mass of the composite body is always m1 + m2 (Fig. 4-12). This additive property of mass may seem obvious, but it has to be verified experimentally. a3 a1 a2 F m1 F F m1+m2 m2 Fig. 4-6 Newton’s Second Law We’ve been careful to state that net force on a body is what causes that body to accelerate. Experiment shows that if a combination of forces F1, F2, F3, ····is applied to as body, the body will have the same acceleration (magnitude and direction) as when only a single force is applied, if that single force is equal to the vector sum F1+F2+F3+ ···· In other words, the principle of superposition of forces also holds true when the net force is not zero and the body is accelerating. Equation (4-5) relates the magnitude of the net force on a body to the magnitude of the acceleration that it produces. We have also seen that the direction of the net force is the same as the direction of the acceleration, whether the body’s path is straight or curved. Newton wrapped up all these relationships and experimental results in a single concise statement that we now call Newton’s second law of motion: If a net external force acts on a body, the body accelerates. The direction of acceleration is the same as the direction of the net force. The net force vector is equal to the mass of the body times the acceleration of the body. In symbols, F ma (4-7) There are at least four aspects of Newton’s second law that deserve special atten-tion. First, Eq. (4-7) is a vector equation. Usually, we will use it in component from, with a separate equation for each component of force and the corresponding acceleration Fx max Fy ma y Fz ma z (4-8) This set of component equations is equivalent to the single vector equation (47). Each component of total force equals the mass times the corresponding component of acceleration. Second, the statement of Newton’s second law refers to external forces. By this we mean forces exerted on the body by other bodies in its environment. It’s impossible for a body to affect its own motion by exerting a force on itself; if it was possible, you could lift yourself to the ceiling by pulling up on your belt! That’s why only external forces are included in the sum F in Eqs. (4-7) and (48). Third, Eqs. (4-7) and (4-8) are valid only when the mass m is constant. It’s easy to think of systems whose masses change, such as a leaking tank truck, a rocket ship, or a moving railroad car being loaded with coal. But such systems are better handled by using the concept of momentum; we’ll get to that in Chapter 8. Finally, Newton’s second law is valid only in inertial frames of reference, just like the first law. Thus it is not valid in the reference frame of any of the Vehicles in Fig. 4-8; relative to any of these frames, the passenger accelerates even though the net force on the passenger is zero. We will usually assume that the earth is an adequate approximation to an inertial frame, although because of its rotation and orbital motion it is not precisely inertial. 4-5 Mass and Weight The weight of a body is a familiar force. It is the force of the earth’s gravitational attraction for the body. We will study gravitational interactions in detail in chapter 12, but we need some preliminary discussion now. The terms mass and weight are often misused and interchanged in everyday conversation. It is absolutely essential for you to understand clearly the distinction between these two physical quantities. Mass characterizes the inertial properties of a body. The weight of a body is a force, a vector quantity. 4-6 Newton’s Third Law A force acting on a body is always the result of its interaction with another body, so forces always come in pairs. In each of these cases the force that you exert on the other body is in the opposite direction to the force that body exert on you. Experiments show that whenever two bodies interact, the two forces that they exert on the other are always equal in magnitude and opposite in direction. This fact is called Newton’s third law of motion. Expressed in words, If body A exerts a force on body B (an “action”), then body B exerts a force on body A (a “reaction”). These two forces have the same magnitude but are opposite in direction. These two forces act on different bodies. (4-11) FAonB FBonA In this statement, “action” and “reaction” are the two opposite forces; we some-times refer to them as an action-reaction pair. This is not meant to imply any cause-and-effect relationship; we can consider either force as the “action” and the other as the “reaction”. We often say simply that the forces are “equal and opposite,” meaning that they have equal magnitudes and opposite direction. We stress that the two forces described in Newton’s third law act on different bodies. This is important in problems involving Newton’s first or second law, which involve the forces that act on a body. 4-7 Using Newton’s Laws Newton’s three laws of motion contain all the basic principles we need to solve a wide variety of problems in mechanics. These laws are very simple in form, but the process of applying them to specific situations can pose real challenges. This section introduces some useful techniques. When you use Newton’s first law, F 0 , for an equilibrium situation, or Newton’s second law, F ma , for a non-equilibrium situation, you must apply it to some specific body. It is absolutely essential to decided at the beginning What body you talking about. This may sound trivial, but it isn’t. Once you have chosen a body, then you have to identify all the forces acting on it. Don’t get confused between the forces acting on a body and the forces exerted by that body on some other body you’ve chosen go into F . To help identify the relevant forces, draw a free-body diagram. What’s that? It is a diagram showing the chosen body by itself, “free” of its surrounding, with vectors down to show the magnitudes and directions of all the forces applied to the body by the various other bodies that interact with it. Be careful to include all the forces acting on the body, but be equally careful not to include any forces that the body exerts on any other body. In particular, the two forces in an action-reaction pair must never appear in the same free-body diagram because they never act on the same body. Furthermore, forces that a body exerts on itself are never include, since these can’t affect on the body’s motion. The cutting-blade assembly on a radial-arm saw has a mass of 5.0 kg. It is pulled along a pair of frictionless horizontal rails aligned with the x-axis by a force Fx. The position of the blade assembly as a function of time is x = (0.18m/s2)t2 – (0.030m/s3)t3 . Find the net force acting on the blade assembly as a function of time. What is the force at time t = 3.0s ? For what times is the force positive? Negative? Zero? Solution Figure 4-24b shows the free-body diagram and coordinate axes. The forces are the horizontal force Fx, the weight w, and the upward force n that the rail exert to support the cutting head. There is no acceleration in the vertical direction, so the sum of the vertical components of forces must be zero. The net forces has only a horizontal component, equal to Fx; from Newton’s second law, this is equal to max. To determine Fx, we first find the acceleration ax by taking the second derivative of x. The second derivative of t2 is 2, and the second derivative of t3 is 6t, so d 2x ax 2 0.36 m 2 0.18 m 3 t s s dt then, from Newton’s second law, Fx = max = (5.0kg)[(0.36m/s3 – (0.18m/s3)]t = 1.8N – (0.90N/s)t y ax(m/s2) Fx(N) Fx x w Figure 4-24(b) 2.00 0.40 1.00 0.20 0 t(s) 1 2 3 4 5 0 -1.00 -0.20 -2.00 -0.40 Figure 4-25(a) t(s) 1 2 3 4 5 Figure 4-25(b) At time t = 3.0s the force is 1.80N – (0.90 N/s)(3.0s) = -0.90N. The force is zero when ax = 0, that is, when 0.36m/s2 – (0.18m/s3)t = 0. This happens when t = 2.0s. When t 2.0s, Fx is positive, and the blade assembly is being pulled to the right. When t > 2.0s, Fx is negative, and the horizontal force on the assembly is to the left. Figure 4-25 shows graphs of Fx and ax as functions of time. You shouldn’t be surprised that the net force and acceleration are directly proportional; according to Newton’s second law, this is always true. 5 Applications of Newton’s Laws 5-1 Introduction Newton’ three laws of motion, the foundation of classic mechanics, can be stated very simply, as we have seen. 5-2 Using Newton’s First Particles In Equilibrium We learned in Chapter 4 that a body is in equilibrium when it is at rest or moving with constant velocity in an inertial frame of reference. When a particle is at rest or is moving with constant velocity in an inertial frame of reference, the net force acting on it---must be zero. (5-1) F 0 We will form: usually use this in component (5-2) Fx 0 Fz 0 Fy 0 This section is about using Newton’s first law to solve problems dealing with bodies in equilibrium. 5-3 Using Newton’s Second Law: Dynamics of Particles We are now ready to discuss dynamics problems, in which we apply Newton’s second law to bodies that are acceleration and hence are not in equilibrium. In this care force on the body is not zero, but is equal to the mass of the body times its acceleration : F m a (5-3) We will use this relation in component form: F max (5-4) Fz ma z Fy ma y 5-4 Frictional Forces we have seen several problems where a body rests or slides on a surface that exerts forces on the body, and we have used the terms normal force and friction force to describe these forces. Whenever two bodies interaction forces constant (touching) of their surfaces, we call the interaction forces contact forces. Normal and friction forces are both contact forces. Kinetic and Static Friction First, when a body rests or slides on a surface, we can always represent the contact force exerted by the surface on the body in terms of components of force perpendicular and parallel to the surface. We call the perpendicular component vector the normal force, denoted by n .(Recall that normal is a synonym for perpendicular) component vector parallel to the surface is the friction force, denoted by f . By definition , n and f are always perpendicular to each other. The direction of the friction force is always such as to oppose relative motion of the two surfaces. The kind of friction that acts when a body slides over a surface is called a kinetic fraction force fk, The adjective “kinetic” and the subscript “k” remind us that the two surfaces are moving relative to each other. The magnitude of the kinetic friction force usually increases when the normal force increases. In many cases the magnitude of the kinetic friction force fk is found experimentally to be approximately proportional to the magnitude n of the normal force. In such case we can write f k k n (5-5) where µk (pronounced “mu-sub-k”) is a constant called the coefficient of kinetic friction. The more slippery the surface, the smaller the coefficient of friction. Because it is a quotient of two force magnitudes, µk is a pure number without units. Friction forces may also act when there is no relative motion. If you try to slide that box of books across the floor, the box may not move at all because the floor exerts an equal and opposite friction force on the box. This is called a static friction force fs. For a given pair of surfaces the maximum value, called (fs)max, is approximately proportional to n; we call the proportionality factor µs (pronounced “mu-sub-s”) the coefficient of static friction. Some representative values of µs are shown in Table 5-1. In a particular situation, the actual force of static friction can have any magnitude between zero (when there is no other force parallel to the surface) and a maximum value given by µsn. In symbols f s sn (5-6) Like Eq. (5-5), this is a relation between magnitudes, not a vector relation. Fluid Resistance and Terminal Speed The direction of the fluid resistance force acting on a body is always opposite the direction of the body’s velocity relative to the fluid. The magnitude of the fluid resistance force usually increases with the speed of the body through the fluid. Contrast this behavior with that of the kinetic friction force between two surfaces in contact, which we can usually regard as independent of speed. For low speeds, the magnitude f of the resisting force of the fluid is approximately proportional to the body’s speed v: (5-7) f kv Where k is a proportionality constant that depends on the shape and size of the body and the properties of the fluid. In motion through air at the speed of a tossed tennis ball or faster, the resisting force is approximately proportional to v2 rather than to v. It is then called air drag or simply drag. In this case we replace Eq.(5-7) f Dv2 (5-8) Because of the v2 dependence, air drag increases rapidly with increasing speed. The air drag on a typical car is negligible at low speeds but comparable to or greater the force of rolling resistance at highway speeds. The value of D depends on the shape and size of the body and on the density of the air. Because of the effects of fluid resistance, an object falling in a fluid will not have a constant acceleration. To describe its motion, we have to start over, using Newton’s second law. The free-body diagram is shown in Fig.5-22. We take the positive direction to be downward and neglect any force associated with buoyancy in the water. There are no x-components, and Newton’s second law gives Fy mg (kv) ma f v a y vt g W=mg O y Fig.5-22 t t O Fig.5-23 O t When the rock first starts to move, v = 0, the resisting force is zero, and the initial acceleration is a = g. As its speed increases, until finally it is equal in magnitude to the weight. At this time, mg – kv = 0, the acceleration becomes zero, and there is no further increase in speed. The final speed vt, called the terminal speed, is given by mg – kvt = 0, or mg vt k Figure 5-23 shows how the acceleration, velocity, and position vary with time. As time goes by, the acceleration approaches zero, and the velocity approaches vt. The slope of the graph of y versus t becomes constant as the velocity becomes constant. To see how the graphs in Fig. 5-23 are derived, we must find the relation between speed and time during the interval before the terminal speed is reached. We go back to Newton’s second law, which we rewrite as dv m mg kv dt After rearranging terms and replacing mg/k by vt, we integrate both sides, noting that v = 0 when t = 0: k t v dv 0 dt 0 v vt m Which integrate to ln and finally vt v k t vt m or v 1 e k / m t vt v vt 1 e k / m t Note that v becomes equal to the terminal speed vt only in the limit that t; the rock cannot attain terminal speed in any finite length of time. The derivative of v gives a as a function of time, and the integral of v gives y as a function of time. We leave the derivations for you to complete, the results are a ge m t k k t m y vt t 1 e m k In deriving the terminal speed in Eq. 5-23, we assumed that the fluid resistance force was proportional to the speed. For an object falling through the air at high speeds, so that the fluid resistance is proportional to v2 as in Eq. (5-8), we invite you to show that the terminal speed vt is given by vt mg D This expression for terminal speed explains the observation that heavy objects in air tend to fall faster than light objects. 5-5 Dynamics of Circular Motion We talked about uniform circular motion in Section 3-5. We showed that when a particle moves in a circular path with constant speed, the particle’s acceleration is always directed toward the center of the circle. The magnitude arad of the acceleration is constant and is given in terms of the speed v and the radius R of the circle by v2 arad R The magnitude of the radial acceleration is given by arad = v2/R, so the magnitude of the net inward radial force Fnet on a particle with mass m must be Fnet marad v2 m R 5-6 The Fundamental Forces of Nature Our current understanding is that all forces are expressions of just four distinct classes of fundamental forces, or interactions between particles. Two are familiar in everyday experience. The other two involve interactions between subatomic particles that we cannot observe with the unaided senses. Of the two familiar classes, gravitational interactions were the first to be studied in detail. The weight of a body results from the earth’s gravitational attraction acting on it. The second familiar class of forces, electromagnetic interaction, includes electric and magnetic forces. All atoms contain positive and negative electric charge, so atoms and molecules can exert electric forces on each other. Contact forces, in-cluding the normal force, friction, and fluid resistance, are the combination of all such forces exerted on the atoms of a body by atoms in its surroundings. These two interactions differ enormously in their strength. The electrical repul-sion between two protons at a given distance is stronger than their gravitational attraction by a factor of the order of 1035. Gravitational forces play no significant role in atomic or molecular structure. But in bodies of astronomical size, positive charge and negative charge are usually present in nearly equal amounts, and the resulting electrical interactions nearly cancel each other out. Gravitational inter-actions are thus the dominant influence in the motion of planets and in the internal structure of stars. The other two interactions are less familiar. One, the strong interaction, is responsible for holding the nucleus of an atom together. Nucleus contain electrically neutral neutrons and positively charged protons. The charged protons repel each other, and a nucleus could not be stable if it were not for the presence of an attrac-tive forces of a different kind that counteracts the repulsive electrical interactions. In this context the strong interaction is also called the nuclear force. It has much shorter range than electrical interactions, but within its range it is much stronger. Finally, there is the weak interaction. It plays no direct role in the behavior of ordinary matter, but it is of vital important interactions among fundamental particles. The weak interaction is responsible for a common form of radioactivity beta-decay, in which a neutron in a radioactive nucleus is transformed in to a proton while ejecting an electron and an essentially massless particle called an antineutrino. During the past several decades a unified theory of the electromagnetic and weak interactions has been developed. 6 Work and Kinetic Energy 6-1 Introduction The new method that we’re about to introduce uses the ideas of work and energy. The applications of these ideas go far beyond mechanics, however. The importance of the energy idea stems from the principle of conservation of energy: Energy is a quantity that can be converted from one form to another but cannot be created or destroyed. We’ll use the energy idea throughout the rest of this book to study a tremendous range of physical phenomena. In this chapter, through, our concentration will be on mechanics. We’ll learn about one important form of energy called kinetic energy, or energy of motion, and how it relates to the concept of work. 6-2 Work In physics, work has a much more precise definition. By making use of the definition we’ll find that in any motion, no matter how complicated, the total work done on a particle by all forces that act on it equals the change in its kinetic energy—a quantity that’s related to the particle’s speed. The physics’s definition of work is based on these observations. Consider a body that undergoes a displacement of magnitude along a straight line. (For now, we will assume that any body we discuss can be treated as a particle so that we can ignore any rotation or changes in shape of the body) While the body moves, a constant force with magnitude F acts on it in the same direction as displacement s. We define the work W done by a constant force F acting on the body under these conditions as W = Fs (6-1) The work done on the body is greater if either the force F or the displacement s is greater. When the force F and the displacement s have different directions, we take the component of F in the direction of the displacement s, and we define the work as the product of this component and magnitude of the displacement. The component of F in the direction of s is F cos, so W = Fscos (6-2) we are assuming that F and are constant during the displacement. If = 0, so that F and s are in the same direction, then cos = 1 and we are back to Eq. 61. Equation (6-2) has the form of the scalar product of two vectors. We can write Eq. (6-2) more compactly as W=F•s (6-3) It’s important to understand that work is a scalar quantity, even through it’s calculated by using two vector quantities (force and displacement). A 5-N force toward the east acting on a body that moves 6 m to the east does exactly the same work as a 5-N force toward the north acting on a body that moves 6 m to It’s also important to realize that work can be positive, negative, or zero. This is the essential way in which work as defined in physics differs from the “everyday” de-finition of work. When the force has a component in the same direction as the dis-placement ( between zero and 90), cos in Eq. (6-2) is positive and the work W is positive. When the force has a component opposite to the displacement ( bet-ween 90° and 180°, cos is negative and the work is negative. When the force is perpendicular to the displacement, = 90° and the work done by the force is zero. F F F F v v n v v F F ф w Fig.6-6 (a) n n n F F w w (b) (c) w (d) 6-3 Work and Kinetic Energy The total work done on a body by external forces is related to the body’s displace-ment, that is, to changes in its position. But the total work is also related to changes in the speed of the body. To see this, consider Fig. 6-6, which shows several examples of a block on a frictionless table. The forces acting on the block are its weight w, the normal force n, and the force F exerted on it by the hand. In Fig. 6-6a the net force on the block is in the direction of its motion. From Newton’s second law, this means that the block speeds up; from Eq. (6-1), this also means that the total work Wtot done on the block is positive. The total work is also positive in Fig.6-6b, but only the component F cos contributes to Wtot. The block again speeds up, and this same component F cos is what causes the acceleration. The total work negative in Fig.6-6c because the net force opposes the displacement; in this case the block slows down. The net force is zero in Fig. 6-6d, so the speed of the block stays the same and the total work done on the block is zero. We can conclude that when a particle undergoes a displacement, it speeds up if Wtot>0, slows down if Wtot<0, and maintains the same speed if Wtot = 0. Let’s make these observations more quantitative. Consider a particle with mass m moving along the x-axis under the action of a constant net force with magnitude F directed along the positive x-axis (Fig. 6-1). The particle’s acceleration is constant and given by Newton’s second law, F = ma. Suppose the speed changes from v1 to v2 while the particle undergoes a displacement s = x2 – x1 from point x1 to x2. Using a constant-acceleration equation, Eq. (2-13), and replacing v0 by v1, v by v2, and (x – x0) by s, we have v22 v12 2as v22 v12 a 2s When we multiply this equation by m and equate ma to the net force F, we find and v22 v12 F ma m 2s 1 2 1 2 Fs mv2 mv1 2 2 (6-4) The product Fs is the work done by the net force F and thus is equal to the total work Wtot done by all the forces acting on the particle. The quantity ½ mv2 is called the kinetic energy K of the particle. 1 2 k mv 2 (6-5) Like work, the kinetic energy of a particle is a scalar quantity; it depends only on the particle’s mass and speed, not its direction of motion. We can interpret Eq. 6-4 in terms of work and kinetic energy. The first term on the right side of Eq. (6-4) is K2 = ½ mv22 , the final kinetic energy of the particle (that is, after the displace-ment). The second term is the initial kinetic energy, K1 = ½ mv12, and difference between these terms is the change in kinetic energy. So Eq. (6-4) says that the work done by the net force on a particle equals the change in the particle’s kinetic energy: Wtot = K2 – K1 = K This result is the work-energy theorem. Because we used Newton’s laws in deriving the work-energy theorem, we can use it only in an inertial frame of reference. The speeds that we use to compute the kinetic energies and the distances that we use to compute work must be measured in an inertial frame. Note also that the work-energy theorem is valid in any inertial frame, but the values of Wtot and K2 – K1 may differ from one inertial frame to another (because the displacement and speed of a body may be diffe-rent in different frame). 6-4 Work and Energy With Varying Forces So far in this chapter we’ve considered work done by constant forces only. But what happens when you stretch a spring? The more you stretch it, the harder you to pull, so the force you exert is not constant as the spring is stretched. We’ve also restricted our discussion to straight-line motion. You can think of many situations in which a force that varies in magnitude, direction or both acts on a body moving along a curved path. We need to be able to compute the work done by the force in these more general cases. Fortunately, we’ll find that the work-energy theorem holds true even when varying forces are considered and when the body’s path is not straight. To add only one complication at a time, let’s consider straight-line motion with a force that is directed along the line but with an x-component F that may change as the body moves. For example, imagine a train moving on a straight track with the engineer constantly changing the locomotive’s throttle setting or applying the brakes. Suppose a particle moves along the x-axis from point x1 to x2. F F x x Fx Fa O x1 x2 x2-x1 x O Fb Fc Fd Δxa Fe Ff F Δxf x2 – x1 Fig. 6-1(a) Fig. 6-11(b) X O x1 x2 x2-x1 Fig. 6-12 x Figure 6-11(a) is a graph of the x-component of force as a function of the particle’s coordinate x. To find the work done by this force, we divide the total displacement into small segments xa, xb and so on average force Fa in that segment multiplied by the displacement xa. We do this for each segment and then add the results for all the segments. The work done by the force in the total displacement from x1 to x2 is approximately W = Fa xa + Fb xb + …. As the number of segments becomes very large and the width of each becomes very small, this sum becomes (in the limit) the integral of F from x1 to x2 : w xx Fdx 2 1 (6-7) Note that Fa xa represents the area of the first vertical strip in Fig. 6-11(b) and that the integral in Eq. (6-7) represents the area under the curve of Fig. 6-11(a) between x1 and x2. On a graph of force as a function of position, the total work done by the force is represented by the area under the curve between the initial and final positions. An alternative interpretation of Eq. (6-7) is that the work W equals the average force that acts over the entire displacement, multiplied by the displacement. Equation (6-7) also applies if F, the x-component of the force, is constant. In that case, F may be taken outside the integral: W x Fdx F x dx F x x x x 2 1 2 1 2 1 but x2 – x1 = s, the total displacement of the particle. So in the case of a constant force F, Eq. (6-7) says that W = Fs, in agreement with Eq. (6-1). The interpret-ation of work as the area under the curve of F as a function of x also holds for a constant force; W = Fs is the area of a rectangle of height F and width s. Now let’s apply what we’ve learned to the stretched spring. If the elongation x is not too great, we find that F is directly proportional to x: F = kx (6-8) where k is a constant called the force constant (or spring constant) of the spring. Equation (6-8) shows that the units of k are force divided by distance, N/m in SI units. The observation that elongation is directly proportional to force for elongations that are not too great was made by Robert Hooke in 1678 and is known as Hooke’s law. It really shouldn’t be called a “law”, since it’s a statement about a specific device and not a fundamental law of nature. To stretch a spring, we must do work. We apply equal and opposite forces to ends of the spring and gradually increase the forces. The force at the moving end does do work. The work done by F when the elongation goes from zero to a maximum value X is F F=kx 1 2 x x w 0 Fdx 0 kxdx kx 2 kx O x x Fig. 6-4 We can also obtain this result graphically. The area of the shaded triangle in Fig.6-14, representing the total work done by the force, is equal to half the pro-duct of the base and altitude, or W 1 x kx 1 kx 2 2 2 This equation also says that the work is the average force kx/2 multiplied by the total displacement X. We see that the total work is proportional to the square of the final elongation X. To stretch an ideal spring by 2 cm, you must do four times as much work as is needed to stretch it by 1 cm. Equation (6-9) assumes that the spring was originally unstretched. If initially the spring is already stretched a distance x1, the work we must do to stretch it to a greater elongation x2 is 1 1 w xx Fdx xx kxdx kx22 kx12 2 2 2 1 2 1 6-10 WORK-ENERGY THEOREM FOR STRAIGHT-LINE MOTION, VARYING FORCES In Section 6-3 we derived the work-energy theorem, Wtot = K2 – K1, for the special case of straight-line motion with a constant net force. We can now prove that this theorem is true even when the force varies with position. As in section 6-3, let’s consider a particle that undergoes a displacement x while being acted on by a net force with x-component F, which we now allow to vary. Just as in Fig. 6-11, we divide the total displacement x into a large number of small segments x. We can apply the work-energy theorem, Eq. (6-6), to each segment because the value of F in each small segment is approximately constant. The change in kinetic energy in segment xa is equal to the work Fa xa , and so on. The total change of kinetic energy is the sum of the changes in the individual segments, and thus is equal to the total work done on the particle during the entire displacement. So Wtot = holds for varying forces as well as for constant ones. Here’s an alternative derivation of the work-energy theorem for a force that may vary with position. It involves making a change of variable from x to v in the work integral. As a preliminary, we note that the acceleration a of the particle can be expressed in various ways, using a = dv/dt, v = dx/dt, and the chain rule for derivatives: dv dv dx dv a v dt dx dt dx (6-11) using this result, Eq. (6-7) tells us that the total work done by the net force F is dv Wtot xx Fdx xx madx xx mv dx (6-12) dx Now (dv/dx)dx is the change in velocity dv during the displacement dx, so in Eq. (6-12) we can substitute dv for (dv/dx)dx. This changes the integration variable from x to v, so we change the limits from x1 and x2 to the corresponding velocities v1 and v2 at these points. This gives us 2 1 2 1 2 1 Wtot vv mvdv 2 1 The integral of v dv is just v2/2. Substituting the upper and lower limits, we finally find 1 1 Wtot mv22 mv12 2 2 (6-13) WORK-ENERGY THEOREM FOR MOTION ALONG A CURVE We can generalize our definition of work further to include a force that varies in direction as well magnitude and a displacement that lies along a curved path. Sup-pose a particle moves from point P1 to P2 along a curve, as shown in Fig. 6-17a. We divide the portion of the curve between these points into many infinitesimal vector displacements, and we call a typical one of these dl. Each dl is tangent to the path at its position. Let F be the force at a typical point along the path, and let be the along between F and dl at this point. Then the small element of work dw done on the particle during the displacement dl may be written as dW = F cosdl = F dl = F•dl , where F = F cos is the component of F in the direction parallel to dl (Fig. 617b). The total work done by F on the particle as it moves from P1 to P2 is then P P P W P F cosdl P F dl P F dl (6-14) 2 2 1 1 2 1 P2 F F P2 F P1 dl Fig. 6-7a P1 dl F = Fcos Fig. 6-7b We can show that the work-energy theorem, Eq. (6-6), holds true even with varying forces and a displacement along a curved path. The force F is essentially constant over any given infinitesimal segment dl of the path, so we can apply the work-energy theorem for straight-line motion to that segment equals the work from dW = F|| dl = Fdl done on the particle. Adding up these infinitesimal quantities of work from all the segments along the whole path gives the total work done, Eq. (6-4), and this equals the total change in kinetic energy over the whole path. So Wtot = K = K2 – K1 is true in general, no matter what the path and no matter what the character of the forces. This can be proved more rigorously by using steps like those in Eqs. (6-11) through (6-13). Note that only the component of the force parallel to the path, F1, does work on the particle, so only this component can change the speed and kinetic energy of the particle. The component perpendicular to the path, F = F sin, has no effect on the particle’s speed; it only acts to change the particle’s direction. The integral in Eq. (6-14) is called a line integral. To evaluate this integral in a speci-fic problem, we need some sort of detailed description of the path and of how F varies along the path. Example 6-9. At a family picnic you are appointed to push your obnoxious cousin Throckmorton in a swing. His weight is w, the length of the chains is R, and you push Throcky until the chains make an angle 0 with the vertical. To do this, you exert a varying horizontal force F that starts at zero and gradually increase just enough so that Throcky and the swing move very slowly and remain very nearly in equilibrium. What is the total work done on Throcky by all forces? What is the work done by the tension T in the chains? What is the work you do by exerting the force F? (Neglect the weight of chains and seat). Solution: The free-body diagram is shown in Fig. 6-18b. We have replaced the tensions in the two chains with a single tension T. Because Throcky is in equilibrium at every point, the net force on him is zero, and the total work done on him by all forces is zero. At any point during the motion the chain force on Throcky is perpendicular to each dl, so the angle between the chain force and the displace-ment is always 90°. Therefore the work done by the chain tension is zero. To compute the work done by F, we have to find out how it varies with the angle . Throcky is in equilibrium at every point, so from Fx = 0 we get y F + (-T sin) = 0, and from Fy = 0 we find T Tcos T cos + (-w) = 0 By eliminating T from these two equations, we obtain F = w tan . F Tsin The point where F is applied swings through the arc s. The arc length s equals the radius R of the circular path w Multiplied by the length (in radians), so s = R. Therefore the displacement dl corresponding to a small change of angle d has a magnitude dl = ds = Rd . The work done by F is W F dl F cosds Now we express everything in terms of the varying angle : W 0 w tan cos Rd wR 0 sin d wR 1 cos 0 0 0 . If 0 = 0, there is no displacement; in that case, cos 0 = 0 and W = wR. In that case the work you do is the same as if you had lifted Throcky straight up a distance R with a force equal to his weight w. In fact, the quantity R(1-cos 0) is the increase in his height above the ground during the displacement, so for any value of 0 the work done by force F is the change in height multiplied by the weight. This is an example of a more general result that we’ll prove in Section 7-2. 6-5 Power When a quantity of work is done might W is done during a time interval t, the average work done per unit or average power Pav is defined to be W Pav (6-15) t The rate at which work is done might not be constant. Even when it varies, we can define instantaneous P as the limit of the quotient in Eq. (6-15) at t approaches zero: W dW t 0 t dt P lim (6-16) The SI unit of power is the watt (W), named for the English inventor James Watt. 7 Potential Energy and Energy Conservation 7-1 Introduction When a dive jumps off a high board into a swimming pool, she hits the water moving pretty fast, with a lot of kinetic energy. Where does that energy come from? The answer we learned in Chapter 6 was that the gravitational force (her weight) does work on the diver as she falls. The diver’s kinetic energyenergy associated with her motion-increase by an amount equal to the work done. But there is a very useful alternative way to think about work and kinetic energy. This new approach is based on the concept of potential energy, which is energy associated with the position of a system rather than its motion. In this approach, there is gravitational potential energy even while the diver is standing on the high board. Energy is not added to the earth-diver system as the diver falls, but rather a storehouse of energy is transformed from one form (potential energy) to another( kinetic energy) as she falls. In this chapter we’ ll see how this transformation can be understand from the work-energy theorem. 7-2 GRAVITATIONAL POTENTIAL ENERGY A particle gains or loses kinetic energy because it interacts with other objects that exert forces on it. We learned in Chapter 6 that during any interaction the change in a particle by the forces that act on it. When a body falls without air resistance, gravitational potential energy decreases and the body’s kinetic energy increases. But in Chapter 6 we used the work-energy theorem to conclude that the kinetic energy of a falling body increases because the force of the earth’s gravity (the body’s weight) does work on the body. Let’s use the work-energy theorem to show that gravitational potential energy. Let’s consider a body with mass m that moves along the (vertical) y-axis, as in Fig 7-1. The forces acting on it are its weight, with magnitude w = mg, and possibly some other forces; we call the vector sum (resultant) of all the other F forces Fother. other Fother y1 W = mg y1 W = mg y2 y2 O Fig 7-1(a) Fig 7-1(b) We’ll assume that the body stays close enough to the earth’s surface that the weight is constant. We want to find the work done by the weight when the body drops from a height y1 above the origin to a lower height y2 (Fig. 7-1a). The weight and displace-ment are in the same direction, so the work Wgrav done on the body by its weight is positive; Wgrav = Fs = w(y2 – y1) = mgy1 – mgy2 (7-1) This expression also gives the correct work when the body moves upward and y2 is greater than y1 (Fig. 7-1b). In that case the quantity (y1 – y2) is negative, and Wgrav is negative because the weight and displacement are opposite in direction. Equation (7-1) shows that we can express Wgrav in terms of the values of the quan-tity mgy at the beginning and end of the displacement. This quantity, the product of the weight mg and the height y above the origin of coordinates, is the gravitational energy, U: U = mgy (7-2) Its initial value is U1 = mgy1 , and its final value is U2 = mgy2 . The change in U is the final value minus the initial value, or U = U2 – U1. We can express the work Wgrav done by the gravitational force during the displacement from y1 to y2 as Wgrav = U1 – U2 = -( U2 – U1 ) = - U (7-3) The negative sign in front of U is essential. When the body moves up, y increase, the work done by the gravitational force is negative, and the gravitational potential energy increase ( U >0). When the body moves down, y decreases, the gravitational force does positive work, and the gravitational potential energy decreases (U<0). Conservation of Mechanical Energy ( Gravitational Force Only ) To see what gravitational potential energy is good for, suppose the body’s weight is the only force acting on it, so Fother = 0. The body is then falling freely with no air resistance and can be moving either up or down. Let its speed at point y1 be v1, and let its speed at y2 be v2. The work-energy theorem, Eq. (6-6), says that the total work done on the body equals the change in the body’s in the body’s kinetic energy; Wtot = K = K2 – K1. If gravity is the only force that acts, then from Eq. (7-3), Wtot = Wgrav = -U = U1 – U2. Pointing there together, we get U or K2 – K1 = U1 – U2 , which we can rewrite as K1 + U1 = K2 + 1 2 1 U2 , (7-4) or mv1 mgy1 mv22 mgy2 (7-5) 2 2 We now define the sum K + U of kinetic and potential energy to be E, the total mechanical energy of the system. By “system” we mean the body of mass m and the earth considered together, because gravitational potential energy U is a shared pro-perty of both bodies. Then E1 = K1 + U1 is the total mechanical energy at y1, and E2 = K2 + U2 is the total mechanical energy at y2. Equation (74) says that when the body’s weight is the only force doing work on it, E1 = E2. Thus is, E is constant; it has the same value at y1 and y2. But since the positions y1 and y2 are arbitrary points in the motion of the body, the total mechanical energy E has the same value at all points during the motion, E = K + U = constant. A quantity that always has the same value is called a conserved quantity. When only the force of gravity does work, the total mechanical energy is constant, that is, is conserved. This is our first example of the conservation of mechanical energy. Effect of Other Force When other forces act on the body in addition to its weight, then Fother in Fig. 7-1 is not zero. The gravitational work Wgrav is still given by Eq. (7-3), but the total work Wtot is then the sum of Wgrav, and the work done by all forces is Wtot = Wgrav + Wother. Equating this to the change in kinetic energy, we have Wother+ Wgrav + = K2 – K1 (7-6) Also, from Eq. (7-3), Wgrav = U1 – U2, so Wother + U1 –U2 = K2 – K1, which we can rearrange in the form K1 + U1 = Wgrav = K2 + U2 (if forces other than gravity do work) (7-7) Finally, using the appropriate expressions for the various energy terms, we obtain 1 2 1 mv1 mgy1 Wother mv22 mgy2 2 2 (7-8) The meaning of Eqs. (7-7) and (7-8) is this: The work done by all forces other than the gravitational force equals the change in the total mechanical energy E = K + U of the system, where U is the gravitational potential energy. Gravitational Potential Energy For Motion Along A Curved Path Fother x y1 y s W = mg W = mg y2 Figure 7-4 (a) (b) the body is acted on by the gravitational force w = mg and possibly by other forces whose resultant we call Fother. To find the work done by the gravitational force during this displacement, we divide the path up into small segments s; a typical segment is shown in Fig. 7-4b. The work done by the gravitational force over this segment is the scalar product of the force and the displacement. In terms of unit vectors, the force is w = mg = -mgj and the displacement is s = xi + yj , so the work done by the gravitational force is w ·s = -mgj·(xi + yj) = - mg y . The work done by gravity is the same as though the body had been displaced ver-tically a distance y, with no horizontal displacement. This is true for every seg-ment, so the total work done by the gravitational force is –mg multiplied by the Total vertical displacement (y2 – y1): Wgrav = - mg( y2 – y1) = mgy1 – mgy2 = U1 – U2 . This work done by gravity is the same as though the body had been displaced ver-tical path. So even if the path a body follows between two points is curved, the total work done by the gravitational force depends only on the difference in height between the two points of the path. This work is unaffected by any horizontal mo-tion that may occur. So we can use the same expression for gravitational potential energy whether the body’s path is curved or straight. 7-3 Elastic Potential Energy We’ll describe the process of storing energy in a deformable body body such as a spring or rubber band in terms of elastic potential energy. A body is called elastic if it returns to its original shape and size after being deformed. To be specific, we’ll consider storing energy in an ideal spring like the ones we discussed in Section 6-4. To keep such an ideal spring stretched by a distance x, we must exert a force F = kx, where k is the force constant of the spring. The ideal spring is a useful idealization because many other elastic bodies show this same direct proportionality between force F and displacement x, provided that x is sufficiently small. We found in Section 6-4 that the work we must do on the spring to move one end form an elongation x1 to a different elongation x2 is 1 1 W kx22 kx12 2 2 (work done on a spring) where k is the force constant of the spring. If we stretch the spring further, we do positive work on the spring; if we let the spring relax while holding one end, we do negative work on it. We also saw that this expression for work is still correct if the spring is compressed, not stretched, so that x1 or x2 or both are negative. Now we need to find the work done by the spring. From Newton’s third law the two quan-tities of work are just negatives of each other. Changing the signs in this equation, we find that in a displacement from x1 to x2 the spring does an amount of work Wel given by 1 1 W kx12 kx22 (work done by a spring) 2 2 Just as for gravitational work, we can express the work done by the spring in terms of a given quantity at the beginning and end of the displacement. This quantity is ½kx2. We can use Eq. (7-9) to express the work Wel done on the block by the elastic force in terms of the change in potential energy: 1 1 Wel kx22 kx12 U1 U 2 U (7-10). 2 2 The work-energy theorem says that Wtot = K2 – K1, no matter what kind of forces are on a body. If the elastic force is the only forces that does work on the body, then Wtot = Wel = U1 – U2. The work-energy theorem Wtot = K2 – K1 then gives us K1 + U1 = K2 + U2 (if only the elastic force does work) (7-11). Here U is given by Eq. (7-9), so 1 2 1 2 1 2 1 2 mv1 kx1 mv2 kx2 (if only the elastic force does work)(72 2 2 12). 2 In this case the total mechanical energy E = K + U (the sum of kinetic and elastic potential energy) is conserved. For Eq. (7-12) to be strictly correct, the ideal spring that we’ve been discussing must also be massless. If the spring has a mass, it will also have kinetic energy as the coils of the spring move back and forth. We can neg-lect the kinetic energy of the spring if its mass is much less than the mass m of the body attached to the spring. For instance, a typical automobile has a mass of 1200 kg or more. The springs in its suspension have masses of only a few kilograms, so their mass can be neglected if we want to study how a car bounces on its suspension. If forces other than the elastic force also do work on the body, we call their work Wother, as before. Then the total work is Wtot = Wel + Wother and the workenergy theorem gives Wel + Wother = K2 – K1 . The work done by the spring is still Wel = U1 – U2, so again K1 + U1 + Wother = K2 + U2 (if forces other than the elastic force do work) (7-13) and 1 2 1 2 1 1 mv1 kx1 Wother mv22 kx22 2 2 2 2 (if forces other than the elastic force do work (7-14). This equation shows that the work done by all forces other than the elastic force equals the change in the total mechanical energy E = K +U of the system, where U is the elastic potential energy. The “system” is made up of the body of mass m and the spring of force constant k. when Wother is positive, E increases; when Wother is negative, E decreases. You should compare Eq. (7-14) to Eq. (7-8), which describes situations in which there is gravitational potential energy but no elastic potential energy. Situations With Both Gravitational And Elastic Potential Energy Equations (7-11), (7-12), (7-13), and (7-14) are valid when the only potential energy in the system is elastic potential energy. What happens when we have both gravitational and elastic forces, such as a block attached to the lower end of a vertically hang-ing spring? We can still use Eq. (7-13), but now U1 and U2 are the initial and final values of the total potential energy, including both gravitational and elastic potential energies. That is, U = Ugrav + Uel. Thus the most general statement of the relationship between kinetic energy, potential energy, and work done by other forces is K1 U grav,1 U el ,1 Wother K 2 U grav, 2 U el , 2 (valid in general) (7-15). That is, the work done by all forces other than the gravitational force or elastic force equals the change in the total mechanical energy E = K + U of the system, where U is the sum of the gravitational potential energy and elastic potential energy. 7-4 Conservative And Non-conservative Forces In our discussions of potential energy we have talked about “storing” kinetic energy by converting it to potential energy. A force that offers this opportunity of two-way conversion between kinetic and potential energies is called a conservative force. We have seen two examples of conservative forces: the gravitational force and the spring force. An essential feature of conservative forces is that their work is always reversible. Anything that we deposit in the energy “bank” can later be with-drawn without loss. Another important aspect of conservative forces is that a body may move from point 1 to point 2 by various paths, but the wok done by a conservative force is the same for all of these paths. Thus if a body stays close to the surface of the earth, the gravitational force mg is independent of height, and the work done by this force depends only on the change in height. If the body moves around a closed path, ending at the same point where it started, the total work done by the gravitational force is always zero. The work done by a conservative force always has these properties: 1. It can always be expressed as the difference between the initial and final values of a potential energy function. 2. It is reversible. 3. It is independent of the body and depends only on the starting and ending points. 4. When the starting and ending points are the same, the total work is zero. When the only forces that do work are conservative forces, the total mechanical energy E = K + U is constant. A force that is not conservative is called a nonconservative force. The work done by a nonconservative force cannot be represented by a potential-energy function. Some nonconservative force, like kinetic friction or fluid resistance, cause mechanical energy to be lost or dissipated; a force of this kind is called a dissipative force. There are also nonconservative forces that increase mechanical energy. The fragments of an exploding firecracker fly off with very large kinetic energy, thanks to a chemical reaction of gunpowder with oxygen. THE LAW OF CONSERVATION OF ENERGY Nonconservative forces cannot be represented in terms of potential energy. But we can describe the effects of these forces in terms of kinds of energy other than kinetic and potential energy. When a car with locked brakes skids to a stop, the tires and the road surface both become hotter. The energy associated with this change in the state of the materials is called internal energy. Raising the temperature of a body increase its internal energy; lowering the body’s temperature of a body decreases its internal energy. To see the significance of internal energy, let’s consider a block sliding on a rough surface. Friction does negative work on the block as it slides, and the change in inter-nal energy of the block and surface (both of which get hotter) is positive. Careful experiments show that the increase in the internal energy is exactly equal to the absolute value of the work done by friction. In other words, Uint = - Wother , where Uint is the change in internal energy. If we substitute this into Eq. (7-7), Eq. (7-13), or (7-15), we find K1 + U1 - Uint = K2 + U2 . Writing K = K2 – K1 and U = U2 – U1, we can finally express this as K + U + Uint = 0 (law of conservation energy) (7-16). This remarkable statement is the general form of the law of conservation. In a given process, the kinetic energy, potential energy, and internal energy of a system may all change. But the sum of those changes is always zero. If there is a decrease in one form of energy, it is made up for by an increase in the other forms. When we ex-pand our definition of energy to include internal energy, Eq. (7-16) says that energy is never created or destroyed; it only changes form. No exception to this rule has ever been found. 7-5 Force and Potential Energy For the two kinds of conservative forces (gravitational and elastic) we have studied, we started with a description of behavior of the force and derived from that an expression for the potential energy. We can reverse this procedure: If we are given a potentialexpression, we can find the corresponding force. W U Let’s apply this to a small displacement x. The work done by the force Fx x during this displacement is approximately equal to Fx x x . We have to say “approximately” because Fx x may vary a little over the interval x. But it is at least approximately true that Fx x x U and F ( x) U . dU x Fx x dx x x Force and Potential Energy in Three Dimensions We can extend this analysis to three dimensions, where the particle may move in the x-, y-, z-direction, or all at once, under the action of a conservative force that has components Fx, Fy , Fz . Each component of force may be a function of the coordinates x, y and z. The potential-energy function U is also a function of all three space coordinates. U FX x Fy U y Fz U z To make these relations exact, we need to take the limits x 0, y 0, and z0. So that these ratios become derivatives. Because U may be a function of all three coordinates, we need to remember that we calculate each of these derivatives, only one coordinate changes at a time. U Fx x U Fy y U Fz z U U U F ( i j k) x y z 8 Momentum Impulse and Collisions 8-1 Introduction A common theme of all these questions is that they can’t be answered by directly applying Newton’s second law, F = ma , because there are forces acting about which we know very litter. Our approach will use two new concepts, momentum and impulse, and a new conservation law, conservation of momentum. This conservation law is every bit as important as that of conservation of energy. The law of conservation of momentum is valid even in situations in which Newton’s laws are inadequate, such as bodies moving at very high speeds (near as the speed of light) or objects on a very small scale (such as the constituents of atoms). Within the domain of Newtonian mechanics, conservation of momentum enables us to analyze many situations that would be very difficult if we tried to use Newton’s laws directly. Among these are collision problems, in which two bodies collide and can exert very large forces on each other for a short time. 8-2 Momentum And Impulse Let’s consider a particle of constant mass m. Because a = dv/dt, we can write Newton’s second law for this particle as dv d mv F m dt dt 8-1 We can take the mass m inside the derivative because it is constant. Thus Newton’s second law says that the net force F acting on a particle equals the time rate of change of the combination mv, the product of the particle’s mass and velocity. We’ll call this combination the momentum, or linear momentum, of the particle. Using the symbol p for momentum, we have p = mv (definition of momentum) (8-2) Momentum is a vector quantity that has a magnitude (mv) and a direction (the same as the velocity vector v). The units of the magnitude of momentum are units of mass times speed; the SI units of momentum are kg·m/s. The plural of momentum is “momenta”. Substituting Eq.(8-2) into Eq.(8.1), we have dp F dt (Newton’s second law in terms of momentum) (8-3). The net force (vector sum of all forces) acting on a particle equals the time rate of change momentum of the particle. This, not F = ma , is the form in which Newton originally stated his second law (though he called momentum the “quantity of motion”). It is valid only in inertial frames of reference. We will often express the momentum of a particle in terms of its components. If the particle has velocity components vx, vy, and vz, its momentum components px, py, , and pz are given by px = mvx , py = mvy , pz = mvz (8-4). These three components equations are equivalent to Eq. (8-2). A particle’s momentum p = mv and its kinetic energy k = ½ mv2 both depend on the mass and velocity of the particle. What is the fundamental difference between these two quantities? A purely mathematical answer is that momentum is a vector whose magnitude is proportional to speed, while kinetic energy is a scalar proportional to the speed squared. But to see the physical difference between momentum and kinetic energy, we must first define a quantity closely related to momentum called impulse. Let’s first consider a particle acted on by a constant net force F during a time interval t from t1 to t2, (We’ll look at the case of varying forces shortly.) The impulse of the net force, denoted by J, is defined to be product of the net force and the time interval: J = F(t2 – t1) = Ft (8-5). Impulse is a vector quantity, its direction is the same aa the net force F . To see what impulse is good for, let’s go back Newton’s second law as restated in terms of momentum, Eq. (8-3). If the net force F is constant, then dp/dt is also constant. In that case, dp/dt is equal to total change in momentum p2 – p1 during the time interval t2 – t1, divided by the interval: P2 P1 F t2 t1 Multiplyingthis equation by (t2 – t1), we have F (t2 t1 ) p2 p1 . Comparing to Eq. (8-5), we end up with a result called the impulse-momentum theorem: J p p 2 1 (impulse-momentum theorem). (8-6) The change in momentum of a particle during a time interval equals the impulse of the net force that acts on the particle during that interval. The impulse-momentum theorem also holds when forces are not constant. To see this, we integrate both sides of Newton’s second law F = dp/dt over time be-tween the limits t1 and t2: t t dp p dt p dp p2 p1 t F dt t dt 2 1 2 1 2 1 The interval on the left is defined to be the impulse J of the net force F during this interval: t t Fdt (general definition of impulse) (8-7). With this definition the impulse-momentum theorem J = P2 – P1 , Eq. (8-6), is va-lid even when the net force F varies with time. We can define an average net force Fav such that even when F is not constant, the impulse J is given by J = Fav( t2 – t1) (8-8). 2 1 When F is constant, F = Fav and Eq. (8-8) reduces to Eq. (8-5). Fx (Fav)x t1 t2 t2-t1 Fig.(8-1) Figure (8-1) shows a graph of the x-component of net force Fx as a function of time during a collision. This might represent the force on a soccer ball that is in contact with a player’s foot from time t1 to t2. The x-component of impulse during this interval is represented by the blue area under the curve between t1 and t2. This area is equal to the rectangular area bounded by t1, t2 , and (Fav)x, so (Fav)x(t2 - t1) is equal to the impulse of the actual time-varying force during the same interval. Impulse and momentum are both vector quantities, and Eqs.(8-5) through (88) are all vector equations. In specific problems it is often easiest to use them in component form: J x tt Fx dt Fav x t2 t1 p2 x p1x mv2 x mv1x J y tt Fy dt Fav y t2 t1 p2 y p1 y mv2 y mv1 y 2 1 2 1 (8-9) MOMENTUM AND KINETIC ENERGY COMPARED We can see now see the fundamental difference between momentum and kinetic energy. The impulse-momentum theorem J = p2 – p1says that changes in a particle’s momentum are due to impulse, which depends on the time over which the net force acts. By contrast, the work-energy theorem Wtot = K2 – K1 tells us that kinetic energy changes when work is down on a particle; the total work depends on the distance over which the net force acts. Consider a particle that starts from rest at t1 so that v1 = 0. Its initial momentum is p1 = mv1 = 0, and its initial kinetic energy is K1 = ½ mv2 = 0. Now let a constant net force equal to F act on that particle from time t1 until time t2. During this interval the particle moves a distance s in the direction of the force. From Eq. (8-6), the particle’s momentum at time t2 is p2 = p1 + J = J, where J = F (t2 – t1) is the impulse that acts on the particle. So the momentum of a particle equals the impulse that accelerated it from rest to its present speed; impulse is the product of the net force that accelerated the particle and the time required for the acceleration. By comparison the kinetic energy of the particle at t2 is K2 = Wtot = Fs, the total work done on the particle to accelerate it from rest. The total work is the product of the net force and the distance required to accelerate the particle. Both the impulse-momentum and work-energy theorem are relationships between force and motion, and both rest on the foundation of Newton’s laws. They are integral particles, relating the motion at two different times separated by a finite interval. By contrast, Newton’s second law itself (in either of the forms F = ma or F = dp/dt) is a differential principle, relating the forces to the rate of change of velocity or momentum at each instant. y y x x FB on A FA on B Fig. 8-6 (b) Fig. 8-6 (c ) 8-3 Conservation of momentum The concept of momentum is particularly important in situations in which we have two or more interacting bodies. Let’s consider first an idealized system consisting of two bodies that interact with each other but not with anything else. Let’s go over that again with some new terminology. For any system, the forces that the particles of the system exert on each other are called internal forces. Forces exerted on any part of the system by some object outside it are called external forces. For the sys-tem we have described, the internal forces are FB on A, exerted by particle B on particle A, and FA on B, exerted by particle A on particle B (Figs. 8-6 b, c). There are no external forces; when this is the case, we have an isolated system. The net force on particle A is FB on A, and the net force on particle B is FA on B, so from Eq. (8-3) the rates of change of the momenta of the two particles are dp A dpB FBonA FAonB (8-10) dt dt The momentum of each particle changes, but these changes are not independent; according to Newton’s third law, the two forces FB on A and FA on B are always equal in magnitude and opposite in direction. That is, FB on A = - FA on B so FB on A + FA on B = 0. Adding together the two equations in Eq. (8-10), we have dp A dpB d PA PB FBonA FAonB 0 dt dt dt (8-11). The rates of change of the two momenta are equal and opposite, so that the rate of change of the vector sum PA + PB is zero. We now define the total momentum P of the system of two particles as the vector sum of the momenta of the individual particles. That is, P = PA + PB (8-12). Then Eq. (8-11) becomes, finally, dp FBonA FAonB 0 dt (8-13) The time rate of change of the total momentum P is zero. Hence the total momentum of the system is constant, even though the individual momenta of the particles that make up the system can change. If external forces are also present, they must be included on the left side of Eq. (8-13) along with the internal forces. Then the total momentum is, in general, not constant. But if the vector sum of the external forces is zero, these forces don’t contribute to the sum, and dp/dt is again zero. Thus we have the following general result: If the vector sum of the external forces on a system is zero, the total momentum of the system is constant. This is the simplest form of the principle of conservation of momentum. This principle is a direct consequence of Newton’s third law. What makes this principle useful is that it doesn’t depend on the detailed nature of the internal forces that act between members of the system. This means that we can apply conservation of momentum even if (as is often the case) we know very little about the internal forces. We have used Newton’s second law to derive this principle, so we have to be careful to use it only in internal frames of reference. We can generalize this principle for a system containing any number of particle A, B, C, … interacting only with each other. The total momentum of such a system is P = PA + PB + = mA vA + mB vB + … (total momentum of a system of particles). We make the same argument as before; the total rate of change of momentum of the system due to each action-reaction pair of internal forces is zero. Thus the total rate of change of momentum of the entire system is zero whenever the vector sum of the exter-nal forces acting on it is zero. The internal forces can change the momentum of individual particle in the system but not the total momentum of the system. 8-4 Inelastic Collisions If the forces between the bodies are much larger than any external forces, as is the case in most collisions, we can neglect the external forces entirely and treat the bodies as an isolated system. Then momentum is conserved in the collision, and the total momentum of the system has the same value before and after the collision. If the forces between the bodies are also conservative, so that no mechanical energy is lot lost or gained in the collision, the total kinetic energy of the system is the same after the collision as before. Such a collision is called an elastic collision. A collision in which the total kinetic energy after the collision is less than that before the collision is called an inelastic collision. An inelastic collision in which the colliding bodies stick together and move as one body after the collision is often called a completely inelastic collision. 8-5 Elastic Collisions From conservation of kinetic energy we have 1 1 1 1 2 2 2 m Av A1 mB vB1 m Av A2 mB vB2 2 2 2 2 2 And conservation of momentum gives mAvA1 mBvB1 mAvA2 mBvB 2 8-7 Rocket Propulsion Momentum considerations are particularly useful for analyzing a system is which the mass of parts of the system change with time. In such case we can’t use Newton’s second law F ma directly because m change. We choose our x-axis to be along the rocket’s direction of motion. The x-component of total momentum at this instant is P1 = mv. In a short time interval da the mass of the rocket changes by an amount dm. This is an inherently negative quantity because the rocket’s mass m decrease with time. During dt a positive mass –dm of burned fuel is ejected from the rocket; Let vex be the exhaust speed of this material relative to the rocket; the burned fuel is ejected opposite the direction of motion, so its xcomponent of velocity relative to the rocket is –vex. The x-component of velocity vfuel of the burned fuel relative to our coordinate system is then v fuel v (vex ) v vex And the x-component of momentum of the ejected mass (-dm) is (dm)v fuel (dm)(v vex ) And the x-component of momentum of the ejected mass (-dm) is (-dm)vfuel = (-dm)(v – vex) The rocket’s momentum at this time is (m + dm)(v+dv). Thus the total x-component of momentum P2 of rocket plus ejected fuel at time t + dt is P2 (m dm)(v dv) (dm)(v vex ) According to our initial assumption, the rocket and fuel are an isolated system. mv (m dm)(v dv) (dm)(v vex ) This can be simplified to mdv dmvex dmdv dv dm m vex dt dt vex dm dv a dt m dt dm F vex dt dm dv vex m m dm dm v0 dv m0 vex m vex m0 m v m m0 m v v0 vex ln vex ln m0 m The ratio m/m0 is the original mass divided by the mass after the fuel has been exhausted. 9 Rotation of Rigid Bodies 9-1 Introduction Real-world bodies can be even more complicated; the forces that act on them can de-form them---stretching, twisting, and squeezing them. We’ll neglect these deformations for now and assume that the body has a perfectly definite and unchanging shape and size. We call this idealized model a rigid body. This chapter and the next are mostly about rotational motion of a rigid body. We begin with kinetic language for describing rotational motion. 9-2 Angular Velocity And Acceleration In analyzing rotational motion, let’s think first about a rigid body that rotates about a fixed axis. By fixed axis we mean an axis that is at rest in some inertial frame of refer-ence and does not change direction relative to that frame. S=r S=r 1rad 1rad P O Fig 9-1 Fig9-2(a) Fig9-2(b) Figure 9-1 shows a rigid body rotating about a fixed axis that passes through point O and is perpendicular to the plane of the diagram, which we choose to call the xy-plane. One way to describe the rotation of this body would be to choose a particular point P on the body and to keep track of the x- and y-coordinates of this point. This isn’t a terribly convenient method, since it takes two numbers (the two coordinates x and y) to specify the rotational position of the body. Instead, we notice that the line OP is fixed in the body and rotates with it. The angle that this line makes with the +x-axis describes the rotational position of the body; we will use this single quantity as a coordinate for rotation. The angular coordinate of a rigid body rotating around a fixed axis can be positive or negative. If we choose positive angles to be measured counterclockwise from the positive x-axis, then the angle in Fig. 9-1 is positive. If we instead choose the positive rotation direction to be clockwise, then in Fig. 9-1 is negative. When we considered the motion of a particle along a straight line, it essential to specify the direction of positive displacement along that line; in discussing rotation around a fixed axis, it’s just as essential to specify the direction of positive rotation. In describing rotational motion, the most natural way to measure the angle is not in degrees, but in radians. As shown in Fig. 9-2a, one radian (1 rad ) is the angle subtended at the center of a circle by an arc with a length equal to the radius of the circle. In Fig9-2b an angle subtended by an arc of length s on a circle of radius r. The value of (in radians) is equal to s divided by r. s r or s=r (9-1) An angle in radians is the ratio of two lengths, so it is a pure number, without dimensions. If s = 3.0 m and r = 2.0 m, then = 1.5, but we will often write this as 1.5 rad to distinguish it from an angle measured in degrees or revolutions. Angular Velocity The coordinate shown in Fig. 9-1 specifies the rotational position of a rigid body at a given instant. We can describe the rotational motion of such a rigid body in terms of the rate of change of . In Fig. 9-3a a reference line OP in a rotating body makes an angle 1 with the +x-axis at time t1. At a later time t2 the angle has changed to 2. We define the average angular velocity av of the body in the time interval t = t2 – t1 as the ratio of the angular displacement = 2 - 1 to t: 2 1 av t2 t1 t The instantaneous angular velocity is limit of av as t approaches zero, that is, the derivative of with respect to t: d lim t 0 t dt any instant, every part of a rotating rigid body has the same angular velocity. The angular velocity is positive if the body is rotating in the direction of increasing and negative if rotating in the direction of decreasing . Angular Acceleration When the angular velocity of a rigid body changes, it has an angular acceleration. If 1 and 2 are the instantaneous angular velocities at times t1 and t2, we define the average angular acceleration av over the interval t = t2 – t1 as the change in angular velocity divided by t: 1 av 2 (9-4). t2 t1 t The instantaneous acceleration is the limit of av as t 0: d lim (9-5). t 0 t dt The usual unit of angular acceleration is the radian per second, or rad/s2. Henceforth we will use the term “angular acceleration” to mean the instantaneous angular acceleration rather than the average angular acceleration. Because = d/dt, we can also express angular acceleration as the second derivative of the angular coordinate: d d d 2 (9-6). dt dt dt 2 In rotational motion, if the angular acceleration is positive, the angular velocity is increasing; if is negative, is decreasing. The rotation is speeding up if and have the same sign and slowing down if and have opposite signs. 9-3 Rotation With Constant Angular Acceleration Let 0 be the angular velocity of a rigid body at time t = 0, and let be its angular velocity at any later time t. The angular acceleration is constant and equal to the average value for any interval. Using Eq. (9-4) with the interval from 0 to t, we find 0 t 0 , or = 0 + t (9-7). The product t is the total change in between t = 0 and the later time t; the angular velocity at time t is the sum of the initial value 0 and this total change. With constant angular acceleration the angular velocity changes at a uniform rate, so its average value between 0 and t is the average of the initial and final values: av 0 2 (9-8). We also know that av is the total angular displacement ( - 0) divided by the time interval (t - 0); av 0 t 0 (9-9). When we equate Eqs. (9-8) and (9-9) and multiply the result by t, we get 1 2 0 0 t (9-10) To obtain a relation between and t that doesn’t contain , we substitute Eq. (9-7) into Eq. (9-10): 1 0 0 0 t t 2 1 2 0 0 t t 2 (9-11). Relating Linear And Angular Kinematics y y ω ω v r P atan r x ω arad x ω Fig 9-7 P Fig 9-8 When a rigid body rotates about a fixed axis, every particle in the body moves in a cir-cular path. The circle lies in a plane perpendicular to the axis and is centered on the axis. The speed of a particle is directly proportional to the body’s angular velocity; the faster the body rotates, the greater the speed of each particle. In Figure 9-7, point P is a constant distance r from the axis of rotation, so it moves in a circle of radius r. At any time the angle (in radians) and the arc length s are related by s = r. We take the time derivative of this, noting that r is constant for any specific particle, and take absolute value of both sides: ds d r dt dt Now ds/dtis the absolute value of the rate of change of arc length, which is equal to the instantaneous linear speed v of the particle. Analogously, d/dt, the absolute value of the rate of change of the angle, is the instantaneous angular speed --- that is, the magnitude of the instantaneous angular velocity in rad/s. Thus v = r (relation between linear and angular speed) (9-13). The farther a point is from the axis, the greater its linear speed. The direction of the linear velocity vector is tangent to its circular path at each point (Fig. (9-7). We can represent the acceleration of a particle moving in a circle in terms of its centri-petal and tangential components, arad and atan (Fig. 9-8), as we did in Section 3-5. It would be a good idea to review that section now. We found that the tangential component of acceleration atan, the component parallel to the instantaneous velocity, acts to change the magnitude of the particle’s velocity (i.e., the speed) and is equal to the rate of change of speed. Taking the derivative of Eq. (9-13), we find atan dv d r r dt dt (9-14). This component of a particle’s acceleration is always tangent to the circular path of the particle. The component of the particle’s acceleration directed toward the rotation axis, the centripetal component of acceleration arad, is associated with the change of direction of the particle’s velocity. In Section 3-5 we worked out the relation arad = v2/r. We can ex-press this in terms of by using Eq. (9-13): v2 arad 2 r (9-15) r The vector sum of the centripetal and tangential components of acceleration particle in a rotating body is the linear acceleration a (Fig. 9-8). 9-5 Energy In Rotational Motion A rotating rigid body consists of mass in motion, so it has kinetic energy. We can ex-press this kinetic energy in terms of the body’s angular velocity and a new quantity called moment of inertia that we will define below. To develop this relationship, we think of the body as being made up of a large number of particles, with masses m1, m2, …, at distances r1, r2, …, from the axis fo rotation. We label the particles with the index i: The mass of the ith particle is mi, and its distance from the axis of rotation is ri. The particles don’t necessarily all lie in the same plane, so we specify that ri is the per-pendicular distance from the axis to the ith particle. When a rigid body rotates about a fixed axis, the speed vi of the ith particle is given by Eq. (9-13), vi = ri, where is the body’s angular speed. Different particles have different values of r, but is the same for all (otherwise, the body wouldn’t be rigid). The kinetic energy of the ith particle can be expressed as 1 1 2 mi vi mi ri 2 2 2 2 The total kinetic energy of the body is the sum of the kinetic energies of all its particles: 1 1 1 k m1r1212 m2 r2222 mi ri 2i2 i 2 2 2 Taking the common factor 2/2 out of this expression, we get 1 1 2 2 2 k m1r1 m2 r2 mi ri 2 2 2 2 i The quantity in parentheses, obtained by multiplying the mass of each particle by the square of its distance from the axis of rotation and adding these products, is denoted by I and is called the moment of inertia of the body for this rotation axis: I m1r12 m2 r22 mi ri 2 (9-16). i The word “moment” means that I depends on how the body’s mass is distributed in space; it has nothing to do with a “moment” of time. For a body with a given rotation axis and a given total mass, the greater the distance from the axis to the particles that make up the body, the greater the moment of inertia. In a rigid body, the distance ri are all constant and I is independent of how the body is rotating around the given axis. In terms of moment of inertia I, the rotational kinetic energy K of a rigid body is 1 K I 2 (rotational kinetic energy of a rigid body) (9-17). 2 The kinetic energy given by Eq. (9-17) is not a new form of energy; it’s the sum of the kinetic energies of the individual particles that make up the rigid body, written in a compact and convenient form in terms of the moment of inertia. When using Eq. (9-17) must be measured in radians per second, not revolutions or degrees per second, to give K in joules; this is because we used vi = ri in our derivation. Equation (9-17) gives a simple physical interpretation of moment of inertia: the greater the moment of inertia, the greater the kinetic energy of a rigid body rotating with a given angular speed . We learned in Chapter 6 that the kinetic energy of a body equals the amount of work done to accelerate that body from rest. So the greater a body’s moment of inertia, the harder it is to start the body rotating if it’s at rest and the harder it is to stop its rotation if it’s already rotating (Fig. 9-12). For this reason, I is also called the rotational inertia. 9-7 Moment of Inertia Calculations When a rigid body cannot be represented by a few point masses but is a continuous distribution of mass, the sum of masses and distance that defines moment of inertia Eq. (9-16) becomes an integral. Imagine dividing the body into small mass elements dm so that all points in a particular element are at essentially the same perpendicular distance from the axis of rotation. We call this distance r, as before. Then the moment of inertia is I r dm 2 (9-20) To evaluate the integral, we have to represent r and dm in terms of the same integration variable. When we have an effectively one-dimensional object, such as the slender rods (a) and (b) in Table 9-2, we can use a coordinate x along the length and relate dm terms of an increment dx volume dV and the density of the body. Density is mass per unit volume, = dm/dv, so we may also write Eq. (9-20) as I r 2 dV If the body is uniform in density, then we may take outside the integral: I r 2 dV (9-21). To use this equation, we have to express the volume element dV in terms of the differentials of the integration variable, such as dV = dxdydz. The element dV must always be chosen so that all points within it are at very nearly the same distance from the axis of rotation. The limits on the integral are determined by the shape and dimensions of the body. For regularly shaped bodies this integration can often be carried out quite easily. 10 Dynamics of Rotational Motion 10-1 Introduction In this chapter we will define a new physical quantity, torque, that describes the twisting or turning effort of a force. We’ll find that the net torque acting on a rigid body determines its angular acceleration, in the same way that the net force on a body determines its linear acceleration. We all also look at work and power in rotational motion in order to understand such problems as how energy is transmitted by rotating drive shaft in a car. Finally, we will develop a new conservation principle, conservation of angular momentum, that is tremendously useful for understanding the rotational motion of both rigid and nonrigid bodies. 10-2 Torque What is it about a force that determines how effective it is in causing or changing rotational motion? The magnitude and direction of the force are important, but so is the position of the point where the force is applied. The quantitative measure of the tendency of a force to cause or change the rotational motion of a body is called torque. Figure 10-2 shows a body that can rotate about an axis that passes through point O and is perpendicular to the plane of the figure. The body is acted on by three forces, F1, F2, and F3, in the plane of the figure. The tendency of F1 to cause a rotation about point O its magnitude F1 Line of action of F1 Lever arm of F1 A l1 F3 o l2 B Lever arm of F2 F2 Line of action of F2 depends on its magnitude F1. It also depends on the perpendicular distance l1 between the line of action of the force (that is, the line along which the vector lies) and point O. We called the distance l1 the lever arm (or moment arm) of force F1 about O. The twisting effort is directly proportional to both F1 and l1. We define the torque (or moment) of the force F1 with respect to point O as the product F1l1. We will use the Greek letter for torque. For a force of magnitude F whose line of action is a perpendicular distance l from the point O, the torque is = Fl (10-1). The lever arm of F1 in Fig. 10-2 is the perpendicular distance OA or l1, and the lever arm of F2 is the perpendicular distance OB or l2. The line of action of F3 passes through the reference point O, so the lever arm for F3 is zero and its torque with respect to point O is zero. Force F1 in Fig. 10-2 tends to cause counterclockwise rotation about O, while F2 tends to cause clockwise rotation. To distinguish between these two possibilities, we will choose a positive sense of rotation. With the choice that counterclockwise torque are positive and clockwise torques are negative, the torques of F1 and F2 about O are 1 = +F1l1 , 2 = F2l2. Figure 10-3 shows a force F applied at a position vector r with respect to the chosen point O. There are several ways to calculate the torque of this force. One is to find the lever arm l and use = Fl. Or we can deter-mine the angle , between the vectors r and F; the lever arm is r sin, so = rF sin. A third method is to represent F in terms of a radial component Frad along the direction of r and a tangential component Ftan at right angles, perpendicular to r. We call this tangential component because if the body rotates, the point where the force acts moves in a circle and this component is tangent to that circle.) Then Ftan = Fsin, and = r (Fsin) = Ftan r. The component Frad has no torque with respect to O because its lever arm with respect to that point is zero. r F 10-3 Torque And Angular Acceleration For A Rigid Body We are now ready to develop the fundamental relation for the rotational dynamics of a rigid body. We will show that the angular acceleration of a rotating rigid body is directly proportional to the sum of the torque components along the axis of rotation. The proportionality factor is the moment of F1,y inertia. F1,tan F1,rad r1 m1 r o Newton’s second law for the tangential component is F1, tan = m1a1,tan (10-4) We can express the tangential acceleration of the first particle in terms of the angular acceleration , using the Eq.(9-4); a1,tan = r1 . Using this relation and multiplying both sides of Eq.(10-4) by r1, we obtain: F1,tan r1 = m1 r12 (10-5) Form Eq.(10-2), F1,tanr1 is just the magnitude of the torque 1 of the net force with respect to the rotation axis. Neither of the components F1,rad or F1y contributes to the torque about the y-axis, since neither tends to change the particle’ rotation about that axis. So 1 = F1,tanr1 is the total torque acting on the particle with respect to the rotation axis. Also, m1r12 is I1, the moment of inertia of the particle about the rotation axis. With this in mind, we rewrite Eq. (10-5) as 1 = I1 = m1 r12. We write an equation like this for every particle in the body and then add all these equations: 1 2 3 m r m r m r 2 11 2 2 2 2 3 3 2 m r i i i I (Rotational analog of Newton’s second law for a rigid body) 10-5 Work And Power In Rotational Motion Suppose a tangential force Ftan acts at the of a pivoted disk. The disk rotates through an infinitesimal angle d about a fixed axis during an infinitesimal time interval dt (Fig, 10-19b). ds R o Ftan d R Ftan The work done by the force Ftan while a point on the rim moves a distance ds is dW = Ftands. If d is measured in radians, then ds = Rd and dW = Ftan Rd. Now FtanR is the torque due to the force Ftan, so dW = d. (10-22) The total work W done by the torque during an angular displacement from 1 to 2 is 2 W d 1 (Work done by a torque). If the torque is constant while the angle changes by a finite amount = 2- 1, then W 2 1 (Work done by a constant torque). When a torque does work on a rotating rigid body, the kinetic energy changes by an amount equal to the work done. d d d ( I )d I d I d Id dt dt Wtot 2 1 1 2 1 2 Id I2 I1 2 2 dW d dt dt dW/dt is the rate of doing work, or power P, and d/dt is angular velocity , so P = . 10-6 Angular Momentum Every rotational quantity that we have encountered in Chapter 9 and 10 is the analog of some quantity in the translational motion of a particle. The analog of momentum of a particle is angular momentum, a vector quantity denoted as L. Its relation to momentum P is exactly the same as the relation of torque to force, = r F. For a particle with constant mass m, velocity v, momentum P = mv, and position vector r relative to the origin O of an inertial frame, we define angular momentum L as L r p r mv (Angular momentum of a particle). P=mv y y mvsin vi=ri o mi ri L=rsin o x x L z z Direction of Li In Fig. 10-20 a particle moves in the xy-plane; its position vector r and momentum p = mv are shown. L mvr sin mvl (10-28) Where l is the perpendicular distance from the line of v to o. when a net force F acts on a particle, its velocity and momentum change, so its angular momentum may also change. We can show that the rate of change of angular momentum is equal to the torque of the net force. dL dr dv mv r m v mv r ma dt dt dt dL (for a particle acted on by net force) r F dt The rate of change of angular momentum of a particle equals the net force acting on it. We can use to find the total angular momentum of a rigid body rotating about the z-axis with angular speed . Li mi (ri )ri mi ri 2 (10-30) The total angular momentum of the slice of the body lying in the xy-plane is the sum Li of the angular momenta Li of the particle. Summing Eq. (10-30), we have L Li ( mi ri2 ) I Where I is the moment of inertia of the slice about the z-axis. The angular velocity vector also lies along the rotation axis, as we discussed at the end of Section 9-2.hence for a rigid body rotating around an axis of symmetry, L and are in the same direction. So we have the vector relationship L I (for a rigid body rotating around a symmetry axis) dL dt (for any system of particle). (10-32) 10-7 Conservation Of Angular Momentum When a system has several parts, the internal forces that the parts exert on each other cause changes in the angular momenta of the parts, but the total angular momentum doesn’t change. Here’s an example. Consider two bodies A and B that interact with each other but not with anything else. Suppose body A exerts a force FAonB on body B; the corresponding torque is AonB . According to Eq. (10-32), this torque is equal to the rate of change of angular momentum of B; AonB dLB dt At the same time, body B exerts a force FBonA on body A, with a corresponding torque dL BonA A dt Form Newton’s third law, FBonA = - FAonB. Furthermore, if the forces act along the same line, their lever arms with respect to the chosen axis are equal. Thus the torques of these two forces are equal opposite, and BonA= -AonB. So if we add the two previous equations, we find dL dLA dLB 0 (zero net external torque) 10-34 0 dt dt dt It also forms the basis for the principle of conservation of angular momentum. When the net external torque acting on a system is zero, the total angular momentum of the system is constant (conserved) 10-8 Gyroscopes And Precession In all of the situations we’ve looked at so far in this chapter, the axis of rotation either has stayed fixed or has moved and kept the same direction. But a variety of new physical phenomena, some quite unexpected, can occur when the axis of rotation can change direction. Periodic Motion 13-1 Introduction The motion repeats itself over and over. We call this periodic motion or oscillation. Understanding periodic motion will be essential for our later study of waves, sound, alternating electric currents, and light. A body that undergoes periodic motion always has a stable equilibrium position. When it is moved away from this position and released, a force or torque comes into play to pull it back toward equilibrium. 13-2 The Causes of Oscillation It’s simplest to define our coordinate system so that the origin O is at the equilibrium position, where the spring is neither stretched nor compressed. Then x is the x-component of the displacement of the body from equilibrium and is also the change in length of the spring. The x-component of acceleration a is given by a = F/m. Whenever the body is displaced from its equilibrium position, the spring force tends to restore it to the equilibrium position. We call a force with this character a restoring force. Oscillation can occur only when there is a restoring force tending to return the system to equilibrium. The amplitude of the motion, denoted by A, is the maximum magnitude of displacement from equilibrium; that is, the maximum value of x. it is always positive. The period, T, is the time for one cycle. It is always positive. The frequency, f, is the number of cycles in a unit of time. It is always positive. The angular frequency, ω, is 2πtimes the frequency: ω=2πf. 13-3 Simple Harmonic Motion The very simplest kind of oscillation occurs when the restoring force F is directly proportional to the displacement from equilibrium x. The x-component of force the spring exerts on the body is the negative of this, so the x-component of force F on the body is F kx (restoring force exerted by an ideal spring) 13-3 This equation gives the correct magnitude and sign of the force, whether x is positive, negative, or zero. When the restoring force is directly proportional to the displacement from equilibrium, as given by 13-3, the oscillation is called simple harmonic motions abbreviated SHM. The acceleration d 2x k a 2 x m dt (simple harmonic motion) 13- 4 The minus sign means the acceleration and displacement always have opposite signs. A body that undergoes simple harmonic motion is called a harmonic oscillator. Equation of Simple Harmonic Motion t A t+ A ·x o x = A cos( t + ) t=0 x 参考圆 (circle of reference) To explore the properties of simple harmonic motion, we must express the displacement x of the oscillating body as a function of time, x(t). The circle in which the ball moves so that its projection matches the motion of the oscillating body is called the circle of reference; we will call the point Q the reference point. We take the circle of reference to lie in the xy-plane, with the origin O at the center of the circle. The x-component of the phasor at time t is just the xcoordinate of the point Q: 13-5 x A cos This is also the x-coordinate of the shadow P, which is the projection Q onto the x-axis. Hence the acceleration of the shadow P along the x-axis is equal to the x-component of the acceleration vector of the reference point Q. aQ 2 A a aQ cos 2 A cos 13-6 13-7 k m 2 k m or (Simple harmonic motion) 1 f 2 2 k m T 1 2 m 2 f k Displacement, Velocity, And Acceleration In SHM We still need to find the displacement x as a function of time for a harmonic oscillator. Equation (13-4) for a body in simple harmonic motion along the x-axis is identical to Eq. (13-8) for the x-coordinate of the reference point in uniform circular motion with constant angular speed k / m . x A cos(t ) (displacement in SHM) 13-13 In simple harmonic motion the position is a periodic sinusoidal function of time. The period T is the time for one complete cycle of oscillation. Thus if we start at time t= 0, the time T to complete one cycle is given by T k T 2 m or T 2 m k The constant in Eq. (13-13) is called the phase angle. It tells us at what point in the cycle the motion was at t = 0. We denote the position at t = 0 by x0. putting t = 0 and x = x0 in equation 13-13, we get x0 A cos dx v A sin(t ) dt dv dx 2 a 2 2 A cos(t ) dt dt 13-14 13-15 13-16 13-4 Energy In Simple Harmonic Motion We can learn even more about simple harmonic motion by using energy consideration. The kinetic energy of the body is K = 1/2mv2, and the potential energy of the spring is U = 1/2kx2. There are no nonconservation forces that do work, so the total mechanical energy E = K + U is conserved; 1 2 1 2 E mv kx cons tan t 2 2 1 2 1 2 1 2 E mv kx kA cons tan t 2 2 2 Total mechanical energy in SHM 13-5 Applications Of Simple Harmonic Motion Vertical SHM Suppose we hang a spring with force constant k and suspend from it a body with mass m. X=0 l F kl mg kl mg Fnet k l x mg kx Angular SHM I I or d 2 2 dt I and 1 f 2 I 13-6 The Simple Pendulum A simple pendulum is an idealized model consisting of a point mass suspended by a massless, unstretchable string. When the point mass is pulled to one side of its straight down equilibrium position and released, it oscillates about The equilibrium position. L T x mgsin m mgcos mg F mg sin x F mg mg L F mg x L k mg / L m m 1 f 2 2 g L g L T 2 1 L 2 f g 13-7 The Physical Pendulum A physical pendulum is any real pendulum, using a body of finite size, as contrasted to the idealized model of the simple pendulum with all the mass concentrated at a single point. (mg )( d sin ) O θ (mgd ) d dsinθ mgsinθ d 2 (mgd ) I I 2 dt mgcosθ mg d 2 mgd 2 I dt 13-8 Damped Oscillations Red-world systems always have some dissipative forces, however, and oscillations do die out with time unless we provide some means for replacing the dissipated mechanical energy. The decrease in amplitude caused by dissipative forces is called damping, and the corresponding motion is called damped oscillation. F kx bv dx d 2x kx b m 2 dt dt k b2 m 4m 2 b 2 km kx bv ma x Ae (b / 2m)t cos( t ) k b2 0 2 m 4m x C1e a1t C 2 e a2t 13-9 Forced Oscillations, Resonance, And Chaos The Tacoma Narrows Bridge collapsed four months and six days after it was opened for traffic. 19 Mechanical Waves 19-1 Introduction Waves can occur whenever a system is disturbed from its equilibrium position and when the disturbance can travel or propagate from one region of the system to another. This chapter and the next two are about mechanical waves, waves that travel within some material called a medium. We’ll begin by deriving the basic equations for describing waves, including the important special case of periodic waves in which the pattern of the wave repeats itself as the wave propagates. Not all waves are mechanical in nature. Another broad class is electromagnetic waves, including light, radio waves, infrared and ultraviolet radiation, x-rays, and gamma rays. No medium is needed for electromagnitude waves; they can travel through empty space. 19-2 Type Of Mechanical Waves A mechanical wave is a disturbance that travels through some material or substance called the medium for the wave. Because the displacements of the medium are perpendicular or transverse to the direction of travel of the wave along the medium, this is called transverse wave. If the motions of the particles of the medium are back and forth along the same direction that the wave travels, we call this a longitudinal wave. t 0 t 0 T 4 T t 2 t t 3 T 4 5 T 4 T 4 t T 2 t 3 T 4 t T t T t t 5 T 4 3 t T 2 t Transverse wave longitudinal wave. 波面 波线 y x 球面波 柱面波 波线 Ray These examples have three things in common. First, in each case the disturbance travels propagates with a definite speed through the medium. This speed is called the speed of propagation, or simply the wave speed. It is determined in each case by the mechanical properties of the medium. We will use the symbol v for wave speed. Second, the medium itself does not travel through space; its individual particles undergo back-and-forth or up-and-down motions around their equilibrium positions. The overall pattern of the wave disturbance is what travels. Third, to set any of these systems into motion, we have put in energy by doing mechanical work on the system. The wave motion transports this energy from one region of the medium to another. Waves transport energy, but not matter, from one region to another. 19-3 Periodic Waves In particular, suppose we move the string up and down in simple harmonic motion with amplitude A, frequency f, angular frequency = 2f, and period T=1/f = 2 / . When a sinusoidal wave passes through a medium, every particle in the medium undergoes simple harmonic motion with the same frequency. For a periodic wave, the shape of the string at any instant is a repeating pattern. The length of one complete wave pattern is the distance from one crest to the next, or from one trough to the next, or from any point to the corresponding point on the next repetition of the wave shape. We call this distance the wavelength of the wave, denoted by . The wave pattern travels with constant speed v and advances a distance of one wavelength in a time interval of one period T. so the wave speed v is given by v = /T, or , because f = 1/T, v = f (periodic wave). 19-4 Mathematical Description Of A Wave For this description we need the concept of a wave function, a function that describes the position of any particle in the medium at any time. We will concentrate on sinusoidal waves, in which each particle undergoes simple harmonic motion about its equilibrium position. Wave Function For A Sinusoidal Wave Suppose that the displacement of a particle at the left end of string (x = 0), where the wave originates, is given by y ( x 0, t ) A sin t A sin 2ft 19-2 The wave disturbance travels from x = 0 to some point x to the right of the origin in an amount of time given by x/v, where v is the wave speed. So the motion of point x at time t is the same as the motion of point x = 0 at the earlier time t – x/v. Hence we can find the displacement of point x at time t by simply replacing t in Equation (19-2) by (t – x/v). x x y ( x, t ) A sin t A sin 2f t v v 19-3 t x y ( x, t ) A sin 2 T 19-4 We get another convenient form of the wave function if we define a quantity k, called the wave number: k 2 vk (wave number) (19-5) (periodic wave) (19-6) y ( x, t ) A sin( t kx) (sinusoidal wave moving in +x-direction) (19-7) y A x Wavelength y A t A Period t1+Δt时刻的波形 u t1时刻的波形 O x x1 x1 x Particle Velocity And Acceleration In A sinusoidal Wave From the wave function we can get an expression for the transverse velocity of any particle in a transverse wave. We call this vy to distinguish it from the wave propagation speed v. To find the transverse velocity vy at a particular point x, we take the derivative of the wave function y(x,t) with respect to t, keeping x constant. If the wave function is y ( x, t ) A sin(t kx) then y ( x, t ) v y ( x, t ) A cos(t kx t (19-9) The acceleration of any particle is the second partial derivative of y(x,t) with respect to t: 2 y( x, t ) 2 2 a y ( x, t ) A sin( t kx ) y( x, t ) 2 t 19-10 We can also compute partial derivatives of y(x,t) with respect to x, holding t constant. 2 y( x, t ) 2 2 k A sin( t kx ) k y( x, t ) 2 x (19-11) Form Eqs.(19-10) and (19-11) and the relation = vk we see that 2 y( x, t ) / t 2 2 2 v 2 y( x, t ) / x 2 k 2 2 y ( x, t ) 1 2 y ( x, t ) 2 2 x v t 2 (wave equation) (19-12) Equation (19-12), called the wave equation, is one of the most important equations in all of physics. 20 Wave Interference and Normal Modes 20-1 Introduction When a wave strikes the boundaries of its medium, all or part of the wave is reflected. When you yell at a building wall or a cliff face some distance away, the sound wave is reflected from the rigid surface, and an echo comes back. When you flip the end of a rope whose far end is tied to a rigid support, a pulse travels the length of the rope and is reflected overlap in the same region of the medium. This overlapping of waves is called interference. 20-2 Boundary Conditions For A String And The Principle Of Superposition As a simple example of wave reflections and the role of the boundary of a wave medium, let’s look again at transverse waves on a stretched string. What happens when a wave pulse or a sinusoidal wave arrives at the end of the string? L 2 L L 3 2 If the end is fastened to a rigid support, it is a fixed end that cannot move. The arriving wave exerts a force on the support; the reaction to this force, exerted by the support on the string, “kicks back” on the string and sets up a reflected pulse or wave traveling in the reverse direction. The conditions at the end of the string, such as a rigid support or the complete absence of transverse force, are called boundary conditions. The formation of the reflected pulse is similar to the overlap of two pulses traveling in opposite directions. The principle of superposition Combining the displacements of the separate pulse at each point to obtain the actual displacement is an example of the principle of superposition; when two waves overlap, the actual displacement of any time is obtained by adding the displacement the point would have if only the first wave were present and the displacement it would have if only the second wave were present. describes the resulting motion in this situation is obtained by adding the two wave functions for the two separate waves. 20-3 Standing Waves On A String We have talked about the reflection of a wave pulse on a string when it arrives at a boundary point. We will again approach the problem by considering the superposition of two waves propagating through the string, one representing the original or incident wave and the other representing the wave reflected at the fixed end. The general term interference is used to describe the result of two or more waves passing through the same region at the same time. Here, instead, the wave pattern in the same position along the string, the amplitude fluctuates. There are particular points called nodes that never move at all. Midway between the nodes is points called antinodes, where the amplitude of motion is greatest. Because the wave pattern doesn’t appear to be moving in either direction along the string, it is called a standing wave. (To emphasize the difference, a wave that does move along the string is called a traveling wave). The principle of superposition explains how the incident and reflected wave combine to form a standing wave. At a node the displacements of the two waves in red and blue are always equal and opposite and cancel each other out. This cancellation is called destructive interference. Midway between the nodes are the points of the greatest amplitude or antinodes, marked A. At the antinodes the displacement of the two waves in red and blue are always identical, giving a large resultant displacement; this phenomenon is called constructive interference. We can see from the figure that the distance between successive nodes or between successive antinodes is one half-wavelength, or 2. We can derive a wave function for the standing wave of Fig. 20-6 by adding the wave functions y1(x, t) and y2(x, t) for two waves with equal amplitude, period, and wavelength traveling in opposite directions. Here y1(x, t) represents an incident wave traveling to the left along the +x-axis, arriving at the point x = 0 and being reflected; y2(x, t) represents the reflected wave traveling to the right from x = 0. We noted in Section 20-2 that the wave reflected from a fixed end of a string is inverted, so we give a negative sign to one of the waves; y1 x, t A sin(t kx) y2 x, t A sint kx (traveling to the left), (traveling to the right). yx, t y1 x, t y2 x, t Asint kx sint kx yx, t y1 x, t y2 x, t 2 A sin kx cos t (20-1) The standing wave amplitude Asw is twice the amplitude A of the original traveling waves: Asw = 2A Equation (20-1) has two factors; a function of x and a function of t. The factor 2Asinkx shows that at each instant the shape of the string is a sine curve. But unlike a wave traveling along a string, the wave shape stays in the same position, oscillating up and down as described by cos t factor. This is in contrast to the phase differences between oscillations of adjacent points that we see with a wave traveling in one direction. We can use Eq. (20-1) to find the positions of the nodes; these are the points for which sin kx = 0, so the displacement is always zero. This occurs when kx =0, , 2, 3, , or, using k = 2, x 0, 2 3 k , , k k 2 3 0, , , 2 2 2 In particular, there is a node at x = 0, as there should be, since this point is a fixed end of the string. A standing wave, unlike a traveling wave, does not transfer energy from one end to the other. The two waves that form it would individually carry equal amounts of power in opposite directions. There is a local flow of energy from each node to the adjacent antinodes and back, but the average rate of energy transfer is zero at every point.