* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Slide 1
Old quantum theory wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Classical mechanics wikipedia , lookup
Internal energy wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Centripetal force wikipedia , lookup
Gibbs free energy wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
Heat transfer physics wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Joseph-Louis Lagrange wikipedia , lookup
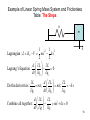
Hunting oscillation wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Equations of motion wikipedia , lookup
Lagrange Equations Use kinetic and potential energy to solve for motion! References http://widget.ecn.purdue.edu/~me563/Lectures/EOMs/Lagrange/In_Focus/page.html System Modeling: The Lagrange Equations (Robert A. Paz: Klipsch School of Electrical and Computer Engineering) Electromechanical Systems, Electric Machines, and Applied Mechatronics by Sergy E. Lyshevski, CRC, 1999. Lagrange’s Equations, Massachusetts Institute of Technology @How, Deyst 2003 (Based on notes by Blair 2002) 1 We use Newton's laws to describe the motions of objects. It works well if the objects are undergoing constant acceleration but they can become extremely difficult with varying accelerations. For such problems, we will find it easier to express the solutions with the concepts of kinetic energy. 2 Modeling of Dynamic Systems Modeling of dynamic systems may be done in several ways: Use the standard equation of motion (Newton’s Law) for mechanical systems. Use circuits theorems (Ohm’s law and Kirchhoff’s laws: KCL and KVL). Today’s approach utilizes the notation of energy to model the dynamic system (Lagrange model). 3 • • • • • • Joseph-Louise Lagrange: 1736-1813. Born in Italy and lived in Berlin and Paris. Studied to be a lawyer. Contemporary of Euler, Bernoulli, D’Alembert, Laplace, and Newton. He was interested in math. Contribution: – Calculus of variations. – Calculus of probabilities. – Integration of differential equations – Number theory. 4 Equations of Motion: Lagrange Equations • There are different methods to derive the dynamic equations of a dynamic system. As final result, all of them provide sets of equivalent equations, but their mathematical description differs with respect to their eligibility for computation and their ability to give insights into the underlying mechanical problem. • Lagrangian method, depends on energy balances. The resulting equations can be calculated in closed form and allow an appropriate system analysis for most system applications. • Why Lagrange: – – – – – Scalar not vector. Eliminate solving for constraint forces (what holds the system together) Avoid finding acceleration. Uses extensively in robotics and many other fields. Newton’s Law is good for simple systems but what about real systems? 5 Mathematical Modeling and System Dynamics Newtonian Mechanics: Translational Motion • The equations of motion of mechanical systems can be found using Newton’s second law of motion. F is the vector sum of all forces applied to the body; a is the vector of acceleration of the body with respect to an inertial reference frame; and m is the mass of the body. • To apply Newton’s law, the free-body diagram (FBD) in the coordinate system used should be studied. F ma Newton approach requires that we find accelerations in all three directions, equate F ma, solve for the constraint forces and then eliminate these to reduce the problem to " characteristic size". 6 Force : Fcoulomb Translational Motion in Electromechanical Systems • Consideration of friction is essential for understanding the operation of electromechanical systems. • Friction is a very complex nonlinear phenomenon and is very difficult to model friction. • The classical Coulomb friction is a retarding frictional force (for translational motion) or torque (for rotational motion) that changes its sign with the reversal of the direction of motion, and the amplitude of the frictional force or torque are constant. • Viscous friction is a retarding force or torque that is a linear function of linear or angular velocity. 7 Newtonian Mechanics: Translational Motion • For one-dimensional rotational systems, Newton’s second law of motion is expressed as the following equation. M is the sum of all moments about the center of mass of a body (Nm); J is the moment of inertial about its center of mass (kg/m2); and is the angular acceleration of the body (rad/s2). M j 8 Newton’s Second Law The movement of a classical material point is described by the second law of Newton: m d 2 r (t ) dt 2 F (r , t ) (r is a vector indicating a position of the material point in space) x r y z Vector F(r, t) represents a force field, which may be calculated by taking into account interactio ns with other particles, or interactio ns with electromag netic waves, or gravitational fields. The second law of Newton is an idealisation, of course, even if one was to neglect quantum and relativist ic effects. There is no justificat ion why only a second time derivative of r should appear in that equation. Indeed if energy is dissipated in the systemusually first time derivatives will appear in the equation too. If a material point loses energy due to EM radiation, third time derivatives will come up. 9 Energy in Mechanical and Electrical Systems • In the Lagrangian approach, energy is the key issue. Accordingly, we look at various forms of energy for electrical and mechanical systems. • For objects in motion, we have kinetic energy Ke which is always a scalar quantity and not a vector. • The potential energy of a mass m at a height h in a gravitational field with constant g is given in the next table. Only differences in potential energy are meaningful. For mechanical systems with springs, compressed a distance x, and a spring constant k, the potential energy is also given in the next table. • We also have dissipated energy P in the system. For mechanical system, energy is usually dissipated in sliding friction. In electrical systems, energy is dissipated in resistors. 10 Electrical and Mechanical Counterparts “Energy” Energy Mechanical Electrical Kinetic (Active) Ke Mass / Inertia 0.5 mv2 / 0.5 j2 Inductor 1 2 1 2 Li Lq 2 2 Potential V Gravity: mgh Spring: 0.5 kx2 Capacitor 0.5 Cv2 = q2/2C Dissipative P Damper / Friction 0.5 Bv2 Resistor 1 2 1 2 Ri Rq 2 2 11 Lagrangian The principle of Lagrange’s equation is based on a quantity called “Lagrangian” which states the following: For a dynamic system in which a work of all forces is accounted for in the Lagrangian, an admissible motion between specific configurations of the system at time t1 and t2 in a natural motion if , and only if, the energy of the system remains constant. The Lagrangian is a quantity that describes the balance between no dissipative energies. L K e V ( K e is the kinetic energy;V is the potential energy) 1 2 mv ; V mgh 2 d L L P Lagrange' s Equation : Qi dt q i qi q i Ke P is power function (half rate at which energy is dissipated); Qi are generalize d external inputs (forces) acting on the systemIf there are three generalize d coordinates, there will be three equations. Note that the above equation is a second - order differenti al equation 12 Generalized Coordinates • In order to introduce the Lagrange equation, it is important to first consider the degrees of freedom (DOF = number of coordinatesnumber of constraints) of a system. Assume a particle in a space: number of coordinates = 3 (x, y, z or r, , ); number of constrants = 0; DOF = 3 - 0 = 3. • These are the number of independent quantities that must be specified if the state of the system is to be uniquely defined. These are generally state variables of the system, but not all of them. • For mechanical systems: masses or inertias will serve as generalized coordinates. • For electrical systems: electrical charges may also serve as appropriate coordinates. 13 Cont.. • Use a coordinate transformation to convert between sets of generalized coordinates (x = r sin cos ; y = r sin sin ; z = r cos ). • Let a set of q1, q2,.., qn of independent variables be identified, from which the position of all elements of the system can be determined. These variables are called generalized coordinates, and their time derivatives are generalized velocities. The system is said to have n degrees of freedom since it is characterized by the n generalized coordinates. • Use the word generalized, frees us from abiding to any coordinate system so we can chose whatever parameter that is convenient to describe the dynamics of the system. 14 For a large class of problems, Lagrange equations can be written in standard matrix form L L P q q q f 1 1 1 1 . . . d . - dt . . . . L L P f n q n q n q n 15 Example of Linear Spring Mass System and Frictionless Table: The Steps k m 1 2 1 2 Lagrangian : L K e V mx kx 2 2 d L L Lagrang' s Equation : 0 dt q i qi L d L L mx; Do the derivatives : mx; kx qi dt qi qi d L L Combine all together : mx kx 0 dt q i qi x 16 Mechanical Example: Mass-Spring Damper 1 2 mx 2 1 V Kx 2 mg h x 2 1 1 L K e V mx 2 Kx 2 mg h x 2 2 1 P Bx 2 2 Ke We have the generalize d coordinate q x, and thus with the applied force Q f , we write the Lagrange equation : d L L P dt x x x d 1 1 ( ( mx 2 Kx 2 mg (h x))) dt x 2 2 1 1 1 ( mx 2 Kx 2 mg (h x)) ( Bx 2 ) x 2 2 x 2 d (mx 2 ) ( Kx mg ) ( Bx ) dt 17 mx Kx mg Bx f Electrical Example: RLC Circuit 1 2 Lq 2 1 2 V q 2C Ke L Ke V P 1 2 1 2 Lq q 2 2C 1 2 Rq 2 We have the generalize d coordinate q (charge), and with the applied force Q u , we have u d L L P dt q q q d 1 2 1 2 1 1 2 1 2 ( ( Lq q )) ( Lq 2 q ) ( Rq ) dt q 2 2C q 2 2C q 2 d Q Q di ( Lq ) Rq Lq Rq L vc Ri dt C C dt i q and q Cvc for a capacitor. This is just KVL equation 18 Electromechanical System: Capacitor Microphone About them see: http://www.soundonsound.com/sos/feb98/articles/capacitor.html This systemhas two degrees of freedom (electrica l and mechanical : charge q and displaceme nt x from equilibriu m) 1 2 1 2 1 2 1 2 Lq mx ; V q Kx 2 2 2C 2 A is the dielectric constant of the air (F/m), C xo x A is the area of the plate, xo - x is the plate separation 1 1 2 1 2 1 2 2 xo x q Kx ; P Rq Bx V 2 A 2 2 2 1 2 1 2 1 1 2 2 xo x q Kx L Lq mx 2 2 2A 2 Ke 19 L L q P mx; Kx; Bx x x 2A x L L xo x q P Lq; ; Rq q q A q Then we obtain the two Lagrange equations q2 mx Bx Kx f 2 A 1 xo x q v Lq Rq A 2 20 Robotic Example q Generalize d coordinates (θ angular position; r radial length; both vary) r Q Applicable forces to each component; is the torque; f is the force f 1 1 J mr 2 ; K e J 2 mr 2 ; V mgr sin 2 2 1 1 The power dissipation : P B1 2 B2 r 2 2 2 1 1 L K e V J 2 mr 2 mgr sin 2 2 P L L P B1 L J mr 2 L mgr cos ; ; q L mr mr q L mr 2 mg sin( ) q P B2 r r r r 21 The Lagrange equation becomes d L L P Q dt q q q mr 2 2mr r mgr cos B1 Q 2 mr mr mg sin( ) B2 r mr 2 0 B1 2mr θ mgr cos( ) m r mr θ B 2 r mg sin( ) f 0 M (q)q V (q, q ) G (q) Q M (q) is the inertia matrix; V (q, q ) is the Coriolis/c entripetal vector G (q) is the gravity vector; Q is the input vector 22 Example: Two Mesh Electric Circuit R1 Ua(t) C1 L1 q1 L2 L12 C2 q2 R2 Assume q1 and q 2 as the independent generalize d coordinates, where q1 is the electric charge in the first loop and q 2 is the electric charge in the second loop. The generalize d force applied to the systemis denoted as Q1 i1 i2 ; q2 ; Q1 U a (t ). s s The total magnetic energy (kinetic energy) is : 1 1 1 2 2 K e L1q1 L12 (q1 q2 ) L2 q 22 2 2 2 We should know that : i1 q1 ; i2 q 2 ; q1 23 K e K e 0; L1 L12 q1 L12 q 2 q1 q1 K e K e 0; L2 L12 q 2 L12 q1 q2 q 2 Use the equation for the total electric energy (potential energy) q q 1 q12 1 q22 V V V ; 1 and 2 2 C1 2 C 2 q1 C1 q2 C 2 The total heat energy dissipated : P 1 1 P P R1q12 R2 q 22 ; R1q1 and R2 q 2 2 2 q1 q 2 K e P V K e P V d K e d K e ( ) Q1 ; ( ) 0 dt q1 q1 q1 q1 dt q2 q2 q2 q2 ( L1 L12 )q1 L12 q2 R1q1 q1 q1 q U a ; - L12 q1 ( L2 L12 )q2 R2 q 2 2 0 C1 C2 q1 q 1 1 L12 q1 2 R2 q 2 R1q1 L12 q2 U a ; q2 ( L1 L12 ) C1 ( L2 L12 ) C2 24 Another Example ia(t) iL(t) R Ua(t) q1 L C uc q2 uL RL Use q1 and q2 as the independent generalize d coordinates : ia q1 ; i L q 2 ; u a (t ) Q1 K e 1 2 K e d K e 0 Lq 2 ; 0; 0; 2 q1 q1 dt q1 K e K e d K e Lq2 0; Lq 2 ; q 2 dt q 2 q 2 Ke 25 2 1 q1 q 2 The total potential energy is : V 2 C q1 q 2 V q1 q 2 V and q1 C q2 C The total dissipated energy is : P P Rq1 and q1 d K e dt q1 1 2 1 Rq1 RL q 22 2 2 P RL q 2 q 2 K e P V d K e K e P V Q1 ; 0 dt q2 q2 q 2 q 2 q1 q1 q1 q q q q2 Rq1 1 2 u a ; L q2 RL q 2 1 0 C C q1 q 2 1 q q2 1 q1 1 u a ; q 2 RL q 2 R C L C By using Kirchhoff' s law, we get duc 1 u c u (t ) di 1 i L a ; L u c RL i L dt C R R dt L 26 Directly-Driven Servo-System r Load TL ir r, Te Rotor Te : electromag netic torque TL : Load torque ur Stator Rr us Lr Ls is ir q1 ; q2 ; q3 r ; s s q1 is ; q 2 ir ; q 3 r ; Q1 u s ; Q2 u r ; Q3 TL is Rs 27 The Lagrange equations are expressed in terms of each independent coordinate K e P V d K e ( ) Q1 dt q1 q1 q1 q1 K e P V d K e ( ) Q2 dt q 2 q2 q 2 q2 K e P V d K e ( ) Q3 dt q3 q3 q3 q3 28 The total kinetic energy is the sum of the total electrical (magnetic) and mechanical (moment of inertia) energies 1 1 1 Ls q12 Lsr q1q 2 Lr q 22 (Electrica l); K em Jq 32 (Mechanical) 2 2 2 1 1 1 2 2 2 K e K ee K em Ls q1 Lsr q1q 2 Lr q2 Jq 3 2 2 2 Ns Nr Ns Nr Mutual inductance : Lsr ( r ) ; LM Lsr max m ( r ) m (90 0 ) K ee Lsr ( r ) LM cos r LM cos q3 ( LM is magnetizin g reluctance) 1 1 1 Ls q12 LM q1q 2 cos q3 Lr q 22 Jq 32 2 2 2 K K The following partial derivatives result : e 0; e Ls q1 LM q 2 cos q3 q1 q1 Ke K e K e K e K e 0; LM q1 cos q3 Lr q 2 ; LM q1q 2 sin q3 ; Jq 3 q 2 q 2 q3 q 3 29 We have only a mechanical potential energy: Spring with a constant ks The potential energy of the spring with constant k s : V 1 k s q32 2 V V V 0; 0; k s q3 q1 q2 q3 The total heat energy dissipated is expressed as : P PE PM 1 1 1 Rs q12 Rr q 22 ; PM Bm q 32 2 2 2 1 1 1 P Rs q12 Rr q 22 Bm q 32 2 2 2 P P P Rs q1 ; Rr q 2 ; and Bm q 3 q1 q2 q3 PE Substituting the original values, we have three differenti al equations for servo - system di di d Ls s LM cos r r LM i r sin r r Rs is u s dt dt dt di di d Lr r LM cos r s LM i s sin r r Rr ir u r dt dt dt d 2 r d r J L i i sin B k s r TL M s r r m 2 dt dt 30 dθ r ω). dt Also, using stator current and rotor current, angular velocity, and position as state variables The last equation should be written in terms of rotor angular velocity ( dis 1 dt Ls Lr L2M cos 2 r 1 2 Rs Lr is LM is r sin 2 r Rr LM ir cos r Lr LM r sin r Lr u s LM cos r u r 2 dir 1 1 1 2 R L i L L i sin R L i L i sin 2 L cos u L u s M s s M s r r r s r M r r M r s s r dt 2 2 Ls Lr L2M cos 2 r d r 1 ( LM is ir sin r Bm r k s r TL ) dt J d r r dt d 1 Considerin g the third equation : r ( LM is ir sin r Bm r k s r TL ) dt J We can obtain the expression for the electromag netic torque Te developed : Te LM is ir sin r 31 More Application Application of Lagrange equations of motion in the modeling of twophase induction motor and generator. Application of Lagrange equations of motion in the modeling of permanent-magnet synchronous machines. Transducers 32































![1. (a) [10 points] Sketch the region bounded by the curves y = −1, y](http://s1.studyres.com/store/data/004842050_1-4c7cc3fcabf5d75968dd69a43581831e-150x150.png)








