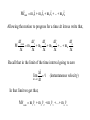Download A 0.300 kg ball is thrown at a frictionless wall, at a 30o angle with

Impulse, momentum (cont.)
y
Top view
A 0.300 kg ball is thrown
x
at a frictionless wall, at a 30o
θ
θ
angle with incident speed of
6 m/s, as shown. After a 4.0 ms
time of contact with the wall,
the ball comes off with a numerically equal angle, at the same speed.
What is the impulse on the ball and average force experienced by the
wall during the collision?
 
For the ball ∆p = Fav ∆t . Since this is a vector expressions we really
have two equations that hold independently along each coordinate
direction:
∆p x = Fxav ∆t
∆p y = Fyav ∆t
&
Top view
vyf
vxi
vyi
ŷ
x̂
θ
vxf
θ
Along x:
m(v xf − v xi=
) m(6
∆p=
x
m
m
o
cos30o − 6 cos30=
) 0
s
s
So no force acts along x (wall is frictionless).
Top view
Along y:
∆p=
m(v yf − v yi )
y
vyf
vxi
vyi
ŷ
x̂
 m
 m
o
o 
m 6 sin 30 −  −6 sin 30  
s


 s
θ
vxf
θ
kg m
∆p y = 1.8
= Fyav ∆t = impulse on ball
s
Then solving for Fyav ,
∆p y
F
=
=
yav
∆t
kg m
s= 450 N
0.004 s
1.8
Average force
on ball
The average force on the wall will be equal but opposite in direction to
this so,
Average force
Fyav = −450 N
on wall
HITT
In better days Maria & Arnold were on their honeymoon afloat on
separate inner tubes, tied together by a 10 m rope. Arnold was
2 times heavier and about 4 times stronger.
A floating cooler had drifted to halfway between them, and they
start a playful tug of war to get to the cooler.
Who gets to the cooler first?
Philanthropist
& ex-wife of
Ex-governor
of CA
Ex-governor
of CA
A) Arnold
B) Maria
C) Its a tie
Maria wins, even if she merely holds on with one hand and Arnold
does all the pulling.
No matter how hard one or the other (or both) pull, they will meet at
their center of mass.
We’ll soon see why this happens. For now we just want to define the
center of mass and learn how to calculated it in various circumstances.
For two objects of mass m1 and m2, the center of mass is a position
along the line connecting the objects from which the distance to each
object d1 and d2 is mass weighted such that:
xcm
m1
d1
d2
m2
m1 d1 = m2 d2
If the masses were connected by a rigid rod and the system suspended
by a knife edge support, the com is the point along the rod at which the
system will balance (also called the center of gravity but only the
same point in a uniform gravitational field).
xcom
m1
d1
d2
m2
m1 d1 = m2 d2
If we had m1= m2= m then the system would balance at d1= d2 = d
and the xcom would lie midway between the objects.
xcom
m
d
d
m
Usually we need to locate the objects and the com within a
coordinate system, hence suppose the two masses lie along
the x axis at positions x1 and x2.
y
xcom
m1
x1
d1
d2
m2
x2
x
y
xcom
m1
d1
x1
In this coordinate system,
x com= x1 + d1
=
x 2 x com + d 2
d2
m2
x2
=
d1 x com − x1
d=
x 2 − x com
2
For the com,
m1 d1 = m2 d2
substituting,
m1 (x com − x1=
) m 2 (x 2 − x com )
rearranging,
m1x com − m1x1 = m 2 x 2 − m 2 x com
m1x com + m 2 x com =
m1x1 + m 2 x 2
x
(m1 + m 2 )x com =
m1x1 + m 2 x 2
Hence with m1 at x1 and m2 at x2 the com is located at,
x com
m1x1 + m 2 x 2
=
m1 + m 2
If there were a third mass m3 at x3 we would find,
x com
m1x1 + m 2 x 2 + m 3x 3
=
m1 + m 2 + m 3
And if there were n masses we would have,
x com
1 n
= ∑ mixi
M i =1
n
where,
M = ∑ mi
i =1
This only considers the masses distributed along the x axis,
more generally, if the masses are distributed in space so that,

mass mi is at position ri = x i xˆ + y i yˆ + z i zˆ

Then, rcom = x com xˆ + y com yˆ + z com zˆ
where,
1 n
x com = ∑ m i x i ,
M i =1
y com
(position of the com)
1 n
1 n
= ∑ m i y i , z com = ∑ m i z i
M i =1
M i =1
Which can also be written


1 n
rcom = ∑ m i ri
M i =1
Vector eqn., gives the above 3 eqns.,
one along each coordinate axis.
y
Example:
m1= 1 kg

r1 =
−2xˆ + 0yˆ
Then:
3
M =∑ m i =1kg + 2 kg + 1.5 kg =4.5 kg
m2= 2 kg

=
r2 2xˆ + 1yˆ
x (meters)
m3= 1.5 kg

=
r3 3xˆ − 2yˆ
i =1

rcom
=

=
rcom

1 n
1
m i ri
[{1kg( −2m) + 2kg(2m) + 1.5kg(3m)}xˆ
=
∑
M i =1
4.5 kg
ˆ
+{1kg(0m) + 2kg(1m) + 1.5kg( −2m)}y]
1
ˆ (1.44m)xˆ − (0.22m)yˆ
[{6.5kg m}xˆ + {−1kg
=
m}y]
4.5 kg
y
m1= 1 kg
m2= 2 kg

=
r2 2xˆ + 1yˆ
x
com


r1 =
−2xˆ + 0yˆ =
rcom (1.44m)xˆ − (0.22m)yˆ
m3= 1.5 kg

=
r3 3xˆ − 2yˆ
Notice that the objects here have different shapes. This doesn’t
matter as long as their positions were given in terms of the
positions of their individual coms (which for symmetric objects,
of uniform density, are at their centers).
Newton’s 2nd law for a system of particles
For a single object we have,


Fnet = ma
Consider the expression for the center of mass,


1 n
rcom = ∑ m i ri
M i =1
Rearranging and expanding, this can be written,





Mrcom= m1 r1 + m 2 r2 + m 3 r3 + ... + m n rn





Mrcom= m1 r1 + m 2 r2 + m 3 r3 + ... + m n rn
Allowing the motion to progress for a time ∆t lets us write that,





∆rcom
∆r3
∆r1
∆r2
∆rn
M = m1
+ m2
+ m3
+ ... + m n
∆t
∆t
∆t
∆t
∆t
Recall that in the limit of the time interval going to zero

∆r 
lim
= v (instantaneous velocity)
∆t →0 ∆t
In that limit we get that,





Mv com= m1v1 + m 2 v 2 + m 3 v 3 + ... + m n v n





Mv com= m1v1 + m 2 v 2 + m 3 v 3 + ... + m n v n
Using this trick again we allow the motion to progress for a time
∆t letting us write that,





∆v com
∆v 3
∆v1
∆v 2
∆v n
M = m1
+ m2
+ m3
+ ... + m n
∆t
∆t
∆t
∆t
∆t
Now in the limit of the time interval going to zero

∆v 
lim
= a (instantaneous acceleration)
∆t →0 ∆t
Taking that limit again we now get that,





Ma com= m1a1 + m 2a 2 + m 3a 3 + ... + m n a n





Ma com= m1a1 + m 2a 2 + m 3a 3 + ... + m n a n
n
The l.h.s. is the total mass of all the particles M = ∑ m i
i =1
times the acceleration of the com of the system of particles.
While the r.h.s. we can recognize as the sum of the individual
forces acting on the individual particles,
  


Ma com = F1 + F2 + F3 + ... + Fn
Included in these forces on the right are all the external forces
acting on the system of particles as well as the internal forces
that the particles exert on one another.
Now comes a key point which makes a critical distinction between
these two types of forces: internal vs. external.
  


Ma com = F1 + F2 + F3 + ... + Fn

All the internal forces can be written as pairwise forces, Fn,m , which
represents the that force particle n experiences due to particle m.
But by Newton’s 3rd law, for
 every such force there must be an equal
and opposite force Fm,n = − Fn,m that particle m experiences due to n.
This means that in our sum on the right all the internal forces will
cancel each other out leaving only the external forces.
  


Ma com = F1 + F2 + F3 + ... + Fn
Hence Newton’s 2nd law for the system of particles is,


Fnet = M a com
Where,

Fnet = the sum of the external forces only.
n
M = the total mass of the system (i.e. M = ∑ m i )
i =1

a com = the acceleration of the center of mass of the system
Note that the com behaves like it is a single point object of mass
 M
(total mass of all the objects) acted upon by the external force Fnet .
Returning to Maria and Arnold, and their tug of war, we can now see
why Maria will always gets to the cooler first. Since no external
forces act,


=
Fnet M
=
a com 0
Which tells us that the center of mass does not move.
The only forces acting are therefore internal forces and we can write,
Fxnet= M a xcom= 0= FxMaria + FxArnold
FxMaria = − FxArnold
m Maria a xMaria = − m Arnold a xArnold
m Maria a xMaria = − m Arnold a xArnold
a xMaria
m Arnold
= −
a xArnold
m Maria
But mArnold = 2mMaria so,
a xMaria
So,
2m maria
= −
a xArnold
m Maria
a xMaria = −2a xArnold
Maria’s acceleration (magnitude) is twice Arnold’s.
We speak of the Moon revolving about the Earth, but this is slightly
inaccurate. Both the Earth and the Moon revolve around their common
com.
Because the Earth is so much more massive than the Moon their
center of mass actually lies within the volume of the Earth (~2/3 of
the way from the center of the Earth).
It is this center of mass that revolves
about the Sun in a slightly elliptical
orbit.
Earth
com
Moon
Sun
Collisions
Types:
Completely elastic: kinetic energy is conserved, at least during
the time of the collision (idealization).
Completely inelastic: energy dissipated in the collision and bodies
stick together after the collision.
In line (direct hit): all motion (before and after along same line)
General: use symmetry to advantage.
Example
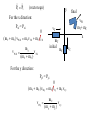
To measure the muzzle velocity of a very high velocity cartridge of
mass mb, it is fired into a much more massive block (mass, mB) that
is initially stationary on an air track. The bullet embeds itself in the
block and the more manageable speed of the two moving off after
the collision is measured to be vf. What was the bullets muzzle
velocity?
vib = ?
bullet, mb
at rest, viB = 0
Block, mB
Use conservation of momentum:
vf
(mb +mB) bullet & block
Pf = Pi
pfb + pfB = pib + piB
pfb + pfB = pib + piB
0
m b v fb + m B v fB = m b v ib + m B v iB
v=
v f so,
& v=
fb
fB
m b vf + m B vf =
m b v ib
(m b + m B )v f =
m b v ib
(m b + m B )
v ib =
vf
mb
vib = ?
bullet, mb
at rest, viB = 0
Block, mB
vf
(mb +mB) bullet & block
Then if the bullet had mass mb =10 g and the block had mass
mB =1 kg and their final speed was measured as 9 m/s,
v ib
(m b + m B )
(0.01 kg + 1.00 kg)
m
vf
(9.00 )
=
mb
0.01 kg
s
v ib = 101(9.00
v ib = 909
vib = ?
bullet, mb
m
)
s
m
s
at rest, viB = 0
Block, mB
vf
(mb +mB) bullet & block
Example
On a completely iced road a car of mass 1000 kg, traveling north
through an intersection at 36 km/hr (10 m/s), collides with a pick-up
truck of mass 2500 kg, traveling east at half that speed. The two
vehicles lock together after the collision.
What is the direction of the wreck and its velocity immediately
after the collision?
y final
vW
mT+ mC
vT
mT
initial m
C
x
vC
 
Pf = Pi
(vector eqn)
y
final
For the x direction:
Pxf = Pxi
(m T + m C )v WX
v WX
vW
mT+ mC
vT
0
=m T v TX + m C v CX
mT
initial m
mT
v TX
=
(m T + m C )
C
For the y direction:
Pyf = Pyi
(m T + m C )v Wy
v Wy
0
=m T v Ty + m C v Cy
mC
=
v Cy
(m T + m C )
x
vC
Then,

vW

vW
y
mC
mT
ˆ
v Tx x +
v Cy yˆ
mT + mC
mT + mC
m
m
ˆ
3.57 x + 2.86 yˆ
s
s
Which has angle (w.r.t. x axis),
final
vW
mT+ mC
vT
x
mT
initial
 2.86 
o
θ Tan
=
38.7


 3.57 
vC
mC
−1
vW
θ
m
3.57
s
And magnitude,
vW =
( 3.57 m / s ) + ( 2.86 m / s )
2
2
m
2.86
s
= 4.57 m / s
No external forces acted in the collision in the plane of the motion.
This means that,


=
Fnet M
=
a com 0


∆v com
y
final
=
a com = 0
∆t
vW
Which implies that
mT+ mC
vT

∆v com =
0
x
m


T
v f com − v i com =
0
initial


v f com = v i com
mC
vC
Which means that whatever the vector velocity of the com before
the collision, the com of the system maintains that same vector
velocity after the collision.
This would be true even if the vehicles separated after the collision.