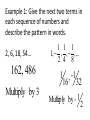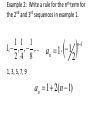Download Honors Geometry Section 1.0 Patterns and Inductive Reasoning

Honors Geometry Section 1.0
Patterns and Inductive Reasoning
Geometry, like much of
mathematics and science,
developed when people began
recognizing and describing
patterns. Much of the reasoning
in geometry consists of three
steps.
1.
Recognize a pattern.
2. Make a conjecture about the pattern.
A conjecture is an educated guess based on
past observations.
3.
Prove the conjecture.
Example 1: Give the next two terms in
each sequence of numbers and
describe the pattern in words.
2, 6, 18, 54…
162, 486
Multiply by 3
1 1 1
1,  , ,  ,...
2 4 8
1 , -1
16 32
Multiply by - 1
2
Example 1: Give the next two terms in
each sequence of numbers and
describe the pattern in words.
1, 3, 5, 7, 9…
11, 13
Add 2
1, 1.1, 21.1, 21.12, 321.12, …
321.123, 4321.123 Add the next larger integer to the
far left and then the far right
A sequence can be specified by an
equation or “rule”. For the first
example (2,6,18,54,…), the sequence
can be specified by the rule
n 1
an  2  3
where n = 1,2,3, etc. corresponding to
the 1st term, 2nd term, 3rd term , etc.
Example 2: Write a rule for the nth term for
the 2nd and 3rd sequences in example 1.
1 1 1
1,  , ,  ,...
2 4 8
 2
an  1  1
1, 3, 5, 7, 9
an  1  2(n  1)
n1
Reasoning based on past observations
is called inductive reasoning.
Keep in mind that inductive reasoning
does not guarantee a correct
conclusion.
Later in the course, we will prove a
conjecture is true using deductive
reasoning. To prove a conjecture is
false, you need to show a single
example where the conjecture is
false. This single example is called a
counterexample.
Example 2: Show the conjecture is false.
The product of two positive numbers is
always greater than the larger number.
1
 7  3.5
1 7  7
2
If m is an integer*, then m2 > 0.
0 0
2
You should know the following sets of numbers:
0,1,2,3,...
integers: ...,2,1,0,1,2,...
whole numbers:
rational numbers:
a
can be written as and a and b are integers
b
irrational numbers:
is not rational