Download Periodic Motion or Oscillations

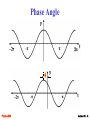
Periodic Motion
or
Oscillations
Physics 232
Lecture 01 – 1
Periodic Motion
Periodic Motion is motion that repeats about
a point of stable equilibrium
Stable Equilibrium
Unstable Equilibrium
A necessary requirement for periodic motion
is a Restoring Force
Physics 232
Lecture 01 – 2
Characteristics
T
A
A
Amplitude - A
The maximum displacement from the equilibrium position
Period - T
The time to complete one cycle of motion, peak to peak or valley to valley
Frequency - f
The number of cycles per unit time
Physics 232
f =
1
T
Lecture 01 – 3
Simple Harmonic Motion
Consider a mass m attached to a
horizontal spring having a spring
constant k with the spring unstretched
We now pull the mass to the right and
then let the mass go
What is the subsequent motion of the mass?
The restoring force is given by Hooke’s Law
Physics 232
F = ma = − k x
Lecture 01 – 4
Simple Harmonic Motion
This is a second order differential equation
d2x
m 2 = −k x
dt
Since this is a second order differential equation, there are
two constants of integration and the general solution is
x = A cos(ω t + φ )
where A is the maximum displacement, φ is a phase angle, and
ω is the angular velocity and is given by
k
ω=
m
A and φ are determined from the initial, boundary, conditions
Physics 232
Lecture 01 – 5
Phase Angle
φ
Physics 232
Lecture 01 – 6
Simple Harmonic Motion
The period of the motion is related to ω by
2π
m
T=
= 2π
k
ω
Note that the period of the motion is independent of the
displacement!
The velocity of the particle is given by
dx
v=
= −ω A sin (ω t + φ )
dt
with the maximum velocity being ω A
Physics 232
Lecture 01 – 7
Simple Harmonic Motion
We have so far that
x = A cos(ω t + φ )
dx
and v =
= −ω A sin (ω t + φ )
dt
The constants A and φ are determined from the initial
conditions, that is what are x and v at a specified time or some
other suitable initial conditions
The maximum displacement occurs when the velocity is zero,
which occurs at the extreme of motion (two locations: x = ±A)
The maximum velocity occurs when the displacement from the
equilibrium position is zero (two values: v = ±ωΑ)
Physics 232
Lecture 01 – 8
SHM – Energy Considerations
We assume that the system is isolated and frictionless
With the force being given by F = − k x
It can be shown that there is a potential energy in the system
that is
1
2
U= kx
2
The total energy is then given by
ETotal = KE + U
1
2 1
= m v + k x2
2
2
Physics 232
Lecture 01 – 9
SHM – Energy Considerations
If we substitute for x and v we find that
ETotal
1
= k A2
2
The total energy is constant
The energy shifts back and forth
between the kinetic energy and
the potential energy, but with the
sum of the two being constant
Physics 232
Lecture 01 – 10
SHM – Energy Considerations
The relationship between kinetic energy, potential energy,
displacement, velocity and acceleration can be seen in the
following diagram
Physics 232
Lecture 01 – 11
Choice of Oscillatory Function
Note that we used the cosine function in our development of
Simple Harmonic Motion
x = A cos(ω t + φ )
We could have also used the sine function for our description
of SHM
x = A sin (ω t + φ ')
The only difference is in the phase angle
Physics 232
Lecture 01 – 12
Simple Harmonic Motion
Simple Harmonic Motion can be used to describe motion in
many situations under appropriate approximations
Any potential energy function that under appropriate
circumstances can be approximated by a parabolic function
will exhibit SHM
Physics 232
Lecture 01 – 13
Simple Pendulum
Consider a mass m suspended from
a massless, unstretchable string of
length L
The forces acting on the mass are as
shown
The “restoring” force is the one
perpendicular to the string
Frestoring = − mg sin θ
But this is a nonlinear function of θ
However for small angles sin θ ≈ θ
We then have that
Frestoring = − mg θ
Physics 232
Lecture 01 – 14
Simple Pendulum
From before we have that Frestoring = − mg θ
We also have that
θ = xL
This then yields that Frestoring
If we then let
k = mg
mg
=−
x
L
L
this is then becomes the equation of SHM
1
The frequency of oscillation is given by f =
2π
g
L
which is independent of the mass attached to the string
Physics 232
Lecture 01 – 15
Damped Motion
Real life situations have dissipative forces
The fact that there is a dissipative force, leads to motion that is
damped, that is the amplitude decreases with time
The dissipative force is often related to the velocity that is in
the motion
Fdiss = −bv
The minus sign indicates that this force is in the opposite
direction to the velocity
The total force is then the sum of the restoring force and this
dissipative force
Fnet = − k x − b v
Physics 232
Lecture 01 – 16
Damped Motion
This net force leads to a slightly more complicated second order
differential equation
d2x
dx
m 2 + b + kx = 0
dt
dt
The exact solution to this equation depends upon the damping
constant
There are three possible solutions
Physics 232
Underdamped:
b < 2 km
Critically Damped:
b = 2 km
Overdamped:
b > 2 km
Lecture 01 – 17
Damped Motion - Underdamped
b < 2 km
The general solution for this situation is given by
2
k
b
−
x = Ae −(b / 2 m ) t cos(ω ' t + φ ) with ω ' =
m 4m 2
This solution looks like
The envelope is the the term
describing the decreasing
amplitude
Envelope = Ae −(b / 2 m )t
Physics 232
Lecture 01 – 18
Damped Motion- Critically Damped
b = 2 km
The general solution for this situation is given by
 b 
 − 2 m  t
t e
b

x = A1 +

 2m 
This solution looks like
Physics 232
Lecture 01 – 19
Damped Motion - Overdamped
b > 2 km
The general solution for this situation is given by
(
x = e −(b / 2 m ) t A1e −ω 2t + A2e −ω 2t
)
b2 k
with ω 2 =
−
4m m
This solution looks like
Physics 232
Lecture 01 – 20
Damped Motion
The most efficient damping, as far getting back to zero
amplitude, is the critically damped case
Note that the overdamped case may yield some interesting
behavior depending on the relative values of the parameters
Physics 232
Lecture 01 – 21
Forced Oscillation
It is also possible to drive a system such as an oscillator with
an external force that is also time varying
The general differential equation is of the form
d2x
m 2 + k x + bv = Fmax cos ω d t
dt
where the term on the right hand side is the driving force
This solution to this equation involves two functions,
a complementary function and a particular solution
Physics 232
Lecture 01 – 22
Forced Oscillation
The solution is given by
x (t ) =
with
(k
Fmax
) + b2ωd2
2 2
− mωd
−1
 2ω d
cos(ω d t − δ )
(b / 2m ) 
δ = tan 
2 
k
m
ω
/
−

d 
δ represents the phase difference between the driving force
and the resulting motion
There can be a delay between the action of the driving force
and the response of the system
Physics 232
Lecture 01 – 23
Resonance
The term in front of the cosine function represents the
amplitude
A=
(k
Fmax
) + b2ωd2
2 2
− mωd
If we vary the angular velocity of the driving force, we find
that the system has its maximum amplitude when
k
ωd ≈
m
This phenomenon of the amplitude peaking at a driving
frequency that is near the natural frequency of the system
is known as resonance
Physics 232
Lecture 01 – 24
Resonance
The strength of the amplitude depends upon the magnitude of
the damping coefficient
The smaller the value of b
the more pronounced the peak
The larger the damping
the peak becomes
broader,
less sharp, and
shifts to lower frequencies
If b > 2k m the peak disappears
completely
Physics 232
Lecture 01 – 25