Download phys1443-spring11

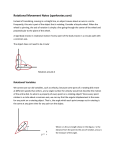
PHYS 1443 – Section 001
Lecture #18
Monday, April 18, 2011
Dr. Jaehoon Yu
•
•
•
•
•
•
Torque & Vector product
Moment of Inertia
Calculation of Moment of Inertia
Parallel Axis Theorem
Torque and Angular Acceleration
Rolling Motion and Rotational Kinetic Energy
Today’s homework is homework #10, due 10pm, Tuesday, Apr. 26!!
Announcements
• Quiz Wednesday, Apr. 20
– Beginning of the class
– Covers from CH9.5 to CH10
• Reading assignment: CH10 – 10.
• Remember to submit your extra credit special project
Monday, April 18, 2011
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
2
Torque
Torque is the tendency of a force to rotate an object about an axis.
Torque, , is a vector quantity.

F
r
P
The line
of Action
d2
d
Moment arm
F2
Consider an object pivoting about the point P by
the force F being exerted at a distance r from P.
The line that extends out of the tail of the force
vector is called the line of action.
The perpendicular distance from the pivoting point
P to the line of action is called the moment arm.
Magnitude of torque is defined as the product of the force
exerted on the object to rotate it and the moment arm.
When there are more than one force being exerted on certain
points of the object, one can sum up the torque generated by each
force vectorially. The convention for sign of the torque is positive
if rotation is in counter-clockwise and negative if clockwise.
Monday, April 18, 2011
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
  rF sin   Fd
  
1
 2
 F1d1  F2d2
3
Ex. 10 – 7: Torque
A one piece cylinder is shaped as in the figure with core section protruding from the larger
drum. The cylinder is free to rotate around the central axis shown in the picture. A rope
wrapped around the drum whose radius is R1 exerts force F1 to the right on the cylinder,
and another force exerts F2 on the core whose radius is R2 downward on the cylinder. A)
What is the net torque acting on the cylinder about the rotation axis?
The torque due to F1
R1
R2
1  R1F1 and due to F2
So the total torque acting on
the system by the forces is
  
1
 2  R2 F2
  2   R1F1  R2 F2
Suppose F1=5.0 N, R1=1.0 m, F2= 15.0 N, and R2=0.50 m. What is the net torque
about the rotation axis and which way does the cylinder rotate from the rest?
Using the
above result
 
Monday, April 18, 2011
 R1F1  R2 F2
 5.0 1.0 15.0  0.50  2.5 N  m
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
The cylinder rotates in
counter-clockwise.
4
Torque and Vector Product
z
Let’s consider a disk fixed onto the origin O and
the force F exerts on the point p. What happens?
rxF
O
r
The disk will start rotating counter clockwise about the Z axis
y
The magnitude of torque given to the disk by the force F is
p
θ
  Fr sin
F
x
But torque is a vector quantity, what is the direction?
How is torque expressed mathematically?
What is the direction?
The direction of the torque follows the right-hand rule!!
The above operation is called the
Vector product or Cross product
What is the result of a vector product?
Another vector
Monday, April 18, 2011
  rF
C  A B
ur ur
ur ur
ur
C  A  B  A B sin 
What is another vector operation we’ve learned?
ur ur
ur ur
Scalar product C  A  B  A B cos
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
Result? A scalar
5
Properties of Vector Product
Vector Product is Non-commutative
What does this mean?
ur ur ur ur
If the order of operation changes the result changes A  B  B  A
ur
Following the right-hand rule, the direction changes ur ur
Vector Product of two parallel vectors is 0.
ur
A  B  B  A
ur
ur ur
ur ur
ur ur
C  A  B  A B sin A B sin 0  0 Thus,
ur ur
AA0
If two vectors are perpendicular to each other
ur ur
ur ur ur ur
ur ur
o
A  B  A B sin  A B sin 90  A B  AB
Vector product follows distribution law


ur ur ur ur ur ur ur
A BC  A B AC
The derivative of a Vector product with respect to a scalar variable is
ur ur
ur
ur
u
r
u
r
d A B
dA
dB

 B A
dt
dt
dt

Monday, April 18, 2011

PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
6
More Properties of Vector Product
The relationship
r r between
r
unit vectors, i, j and k
r r r r
r r
i  i  j  j  k  k 0
r r
r r r
i  j  j  i  k
r r r
r r
j  k  k  j i
r
r r
r r
k  i  i  k  j
Vector product of two vectors can be expressed in the following determinant form
ur ur
AB
r
i
r
j
r
k
Ax
Ay
Az
Bx
By
Bz

 Ay Bz  Az By
Monday, April 18, 2011

r
i
Ay
Az
By
Bz
r
j
Ax
Az
Bx
Bz
r
k
Ax
Ay
Bx
By
r
r
r
i Ax Bz  Az Bx  j  Ax By  Ay Bx k

PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu

7
Moment of Inertia
Rotational Inertia:
For a group
of particles
Measure of resistance of an object to
changes in its rotational motion.
Equivalent to mass in linear motion.
I   mi ri2
i
What are the dimension and
unit of Moment of Inertia?
For a rigid
body
I   r 2 dm
 ML  kg  m
2
2
Determining Moment of Inertia is extremely important for
computing equilibrium of a rigid body, such as a building.
Dependent on the axis of rotation!!!
Monday, April 18, 2011
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
8
Example for Moment of Inertia
In a system of four small spheres as shown in the figure, assuming the radii are negligible
and the rods connecting the particles are massless, compute the moment of inertia and
the rotational kinetic energy when the system rotates about the y-axis at angular speed ω.
y
m
Since the rotation is about y axis, the moment of
inertia about y axis, Iy, is
b
l
M
O
l
2
2
2
2
2
2
I

m

0

m

0

m
r

2Ml

Ml

Ml
 ii
x
M
b
m
i
This is because the rotation is done about y axis,
and the radii of the spheres are negligible.
1 2 1
K R  I  2Ml 2  2  Ml 2 2
2
2
Why are some 0s?

Thus, the rotational kinetic energy is

Find the moment of inertia and rotational kinetic energy when the system rotates on
the x-y plane about the z-axis that goes through the origin O.

2
2
2
I   mi ri 2  Ml 
Ml 2 mb2 mb 2  2 Ml  mb
i
Monday, April 18, 2011

1
1
K R  I 2  2Ml 2  2mb2  2  Ml 2  mb2  2
2
2
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
9
Calculation of Moments of Inertia
Moments of inertia for large objects can be computed, if we assume
the object consists of small volume elements with mass, mi.
2
2
I

lim
r
m

r

i
i
The moment of inertia for the large rigid object is
 dm
m 0
i
i
It is sometimes easier to compute moments of inertia in terms
How can we do this?
of volume of the elements rather than their mass
Using the volume density,  , replace   dm
dm  dV The moments of
2
I


r
dV
 dV
dm in the above equation with dV.
inertia becomes
Example: Find the moment of inertia of a uniform hoop of mass M and radius R
about an axis perpendicular to the plane of the hoop and passing through its center.
y
O
The moment
of inertia is
dm
R
Monday, April 18, 2011
x
What do you notice
from this result?
I   r 2 dm  R2  dm  MR 2
The moment of inertia for this
object is the same as that of a
point of mass M at the distance R.
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
10
Ex.10 – 11 Rigid Body Moment of Inertia
Calculate the moment of inertia of a uniform rigid rod of length L and mass M about an
axis perpendicular to the rod and passing through its center of mass.
M


The line density of the rod is
y
L
M
so the masslet is
dm  dx  dx
L
dx
x
x
L
The moment
of inertia is
M  L 
 L

     
 2
3L  2 
3
What is the moment of inertia
when the rotational axis is at
one end of the rod.
Will this be the same as the above.
Why or why not?
Monday, April 18, 2011
L /2
M 1 3
x2 M

x 

r
dm
I 

dx

 L /2
L  3  L / 2
L
L /2
2
I
3
 M  L3  ML2

 4  
3L
12

L
M 1 3
x2 M
2

x 
dx
 r dm  0

L  3 0
L
2
M
M 3
ML
3
 L   0  

L 



3L
3L
3

L
Since the moment of inertia is resistance to motion, it makes perfect sense
for it to be harder to move when it is rotating about the axis at one end.
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
11
Parallel Axis Theorem
Moments of inertia for highly symmetric object is easy to compute if the
rotational axis is the same as the axis of symmetry. However if the axis of
rotation does not coincide with axis of symmetry, the calculation can still be
done in a simple manner using parallel-axis theorem. I  I CM  MD 2
y
Moment of inertia is defined as
r
yCM
y
y’
(x,y)
D
xCM
What does this
theorem
tell you?
Monday, April 18, 2011

x  xCM  x ' y  yCM  y'
One can substitute x and y in Eq. 1 to obtain
2
2
I   xCM  x'  yCM  y'  dm


CM
2
2
2
2
(xCM,yCM)
 xCM
 yCM
dm

2x
x'dm

2y
y'dm

x'

y'
dm
CM
CM





x’
x
Since x and y are

I   r 2 dm   x 2  y 2 dm (1)



Since the x’ and y’ are the
 x' dm  0  y' dm  0
x distance from CM, by definition
Therefore, the parallel-axis theorem
2
2
I  xCM
 yCM
 dm   x'2  y'2 dm  MD2  ICM
Moment of inertia of any object about any arbitrary axis are the same as
the sum ofPHYS
moment
of inertia
1443-001,
Spring for
2011a rotation about the CM and that
12of
Dr. Jaehoon
Yu axis.
the CM about the
rotation
Example for Parallel Axis Theorem
Calculate the moment of inertia of a uniform rigid rod of length L and mass M about an
axis that goes through one end of the rod, using parallel-axis theorem.
The line density of the rod is  
y
so the masslet is
CM
dm  dx 
dx
x
L
x The moment of
inertia about
the CM
M
L
M
dx
L
L /2
I CM
M 1 3
x2 M
2
x 
  r dm  
dx 

 L /2
L
3

 L / 2
L
L /2
3
3
M  L 
 L   M  L3  ML2


      
 2   3L  4 
3L  2 
12
2
Using the parallel axis theorem
I  I CM
ML2  L 
ML2 ML2 ML2
2
 D M
  M 




12
2
12
4
3
The result is the same as using the definition of moment of inertia.
Parallel-axis theorem is useful to compute moment of inertia of a rotation of a rigid
object with complicated shape about an arbitrary axis
Monday, April 18, 2011
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
13
Check out
Figure 10 – 20
for moment of
inertia for
various shaped
objects
Monday, April 18, 2011
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
14
Torque & Angular Acceleration
Ft
r F
r
Let’s consider a point object with mass m rotating on a circle.
What forces do you see in this motion?
m
The tangential force Ft and the radial force Fr
Ft  mat  mr
The torque due to tangential force Ft is   F r  ma r  mr 2  I
t
t
The tangential force Ft is
What do you see from the above relationship?
What does this mean?
  I
Torque acting on a particle is proportional to the angular acceleration.
What law do you see from this relationship?
Analogs to Newton’s 2nd law of motion in rotation.
How about a rigid object?
The external tangential force δFt is d Ft  d mat  d mr
dFt
2
r
dm 
d
F
r

d

The
torque
due
to
tangential
force
F
is
t
t
δm
The total torque is   lim  d   d   lim  r 2d m    r 2 dm  I
d 0
d m0
r
Contribution from radial force is 0, because its
What is the contribution due
line of action passes through the pivoting
O
to
radial
force
and
why?
Monday, April 18, 2011
PHYS 1443-001, Spring 2011point, making the moment arm 0.
15

Dr. Jaehoon Yu

Rolling Motion of a Rigid Body
What is a rolling motion?
A more generalized case of a motion where the
rotational axis moves together with an object
A rotational motion about a moving axis
To simplify the discussion, let’s
make a few assumptions
1.
2.
Limit our discussion on very symmetric
objects, such as cylinders, spheres, etc
The object rolls on a flat surface
Let’s consider a cylinder rolling on a flat surface, without slipping.
Under what condition does this “Pure Rolling” happen?
The total linear distance the CM of the cylinder moved is sR
R  s
s=Rθ
Monday, April 18, 2011
Thus the linear
speed of the CM is
ds d
vCM  R R

dt
dt
The condition for a “Pure Rolling motion”
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
16
More Rolling Motion of a Rigid Body
The magnitude of the linear acceleration of the CM is
P’
CM
dvCM
d
aCM 
R
R

dt
dt
As we learned in rotational motion, all points in a rigid body
2vCM moves at the same angular speed but at different linear speeds.
vCM
CM is moving at the same speed at all times.
At any given time, the point that comes to P has 0 linear
speed while the point at P’ has twice the speed of CM
P
Why??
A rolling motion can be interpreted as the sum of Translation and Rotation
P’
CM
P
vCM
P’
vCM
CM
v=0
vCM
Monday, April 18, 2011
+
v=Rω
v=Rω
2vCM
P’
=
P
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
CM
vCM
P
17
Kinetic Energy of a Rolling Sphere
Let’s consider a sphere with radius R
rolling down the hill without slipping.
R

h
θ
vCM
Since vCM=Rω
What is the speed of the
CM in terms of known
quantities and how do you
find this out?
Monday, April 18, 2011
1
2 1
R22
K ICM  M
2
2
2
1 2
1 v
C
M
 ICM   MvCM
2  R 2
1
I
CM 2
 2 
M
v

CM
2
R


Since the kinetic energy at the bottom of the hill must
be equal to the potential energy at the top of the hill
1
I
CM 2
Mgh

M
v
 2

K
CM
2
R

PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
2
gh
v

CM
2
1

I
/MR
CM
18
Ex. 10 – 16: Rolling Kinetic Energy
For solid sphere as shown in the figure, calculate the linear speed of the CM at the
bottom of the hill and the magnitude of linear acceleration of the CM. Solve this problem
using Newton’s second law, the dynamic method.
What are the forces involved in this motion?
Gravitational Force, Frictional Force, Normal Force
Newton’s second law applied to the CM gives
n
f
M
h
Mg
Mg
sin


fMa
F 
n

Mg
cos

0
F 
θ
x
CM
y
Since the forces Mg and n go through the CM, their moment arm is 0
  fRICM

and do not contribute to torque, while the static friction f causes torque CM
We know that
2 2
ICM
 MR
5
a

R

CM
Monday, April 18, 2011
We
obtain
2 2
MR
ICM
aCM 2Ma
f 
5
CM
R  R  R 5


Substituting f in
dynamic equations
5
7
a

g
sin

Mg
sin
Ma
CM CM
7
5
PHYS 1443-001, Spring 2011
Dr. Jaehoon Yu
19