* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download L. Fortunato - INFN Padova
Quantum chromodynamics wikipedia , lookup
Density matrix wikipedia , lookup
Self-adjoint operator wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Casimir effect wikipedia , lookup
Renormalization group wikipedia , lookup
Atomic theory wikipedia , lookup
Compact operator on Hilbert space wikipedia , lookup
History of quantum field theory wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Rotational–vibrational spectroscopy wikipedia , lookup
Scalar field theory wikipedia , lookup
Two-dimensional conformal field theory wikipedia , lookup
Lie algebra extension wikipedia , lookup
Vertex operator algebra wikipedia , lookup
Canonical quantization wikipedia , lookup
The algebraic way to molecular structure
Introductory Lecture given at National Institute of Chemical Physics and Biophysics , Tallinn, Estonia (Feb 2017)
Lorenzo Fortunato – Padova Univ. (Italy) & I.N.F.N.
H2
University of Padova,
Italy (founded 1222)
Dept. of Physics and
Astronomy
+
National Insitute of
Nuclear Physics
Summary
Online at:
www.pd.infn.it/~fortunat/lectures.html
• Why Lie algebras allow to write meaningful model
hamiltonians
• Dynamical symmetries and spectrum generating
algebra
• Examples (useful for Molecular Physics):
Angular momentum
Rigid rotor
SO(3) : CO molecule
The U(4) vibron model for diatomic molecules
• Seminar:
The algebraic approach to endohedral molecules
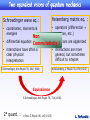
Two equivalent visions of quantum mechanics
Schroedinger wave eq.:
Heisenberg matrix eq. :
• coordinates, momenta &
energies
• operators (differential
matrices, etc.)
• interactions have often a
clear physical
interpretation
• interactions are more
general, but sometimes
difficult to intepret
Non
• equations
are algebrized
• differential equation Commutativity
!
E.Schroedinger, Ann.Physik 79, 361 (1926)
W.Heisenberg, Z.Physik 33, 879 (1925)
Equivalence
E.Schroedinger, Ann.Physik 79, 734 (1926)
2° quant. :
V.Fock, Z.Physik 98, 145 (1935)
L. Fortunato
Example: Angular Momentum so(3)
L =r p
[Lx , Ly ] = iLz
Lx , Ly , Lz
are generators of so(3)
+cyclic permutations over indices
C[so(3)] = L2= Lx2 + Ly2 + Lz2
is the quadratic Casimir operator (rank 1)
[C , Li ] = 0 , Li SO(3)
so(3) so(2)
L
M
|
Branching problem
Branching rules:
-L M L
L. Fortunato
… continues ...
One must specify the action of the generators on a
given orthonormal basis |LM
L±|LM = [(LM)(L±M+1)]½|LM±1
iLy
L± = Lx ±
Lz|LM = M|LM
L2|LM = L(L+1)|LM
Application in the rigid rotor:
H=k L²
E=k L(L+1)
with k=(h²/2I)
Notice it is the Casimir operator of SO(3)
L. Fortunato
… quantum rotors
H2
HCl,
CO, etc.
EJ= B J(J+1)
EJ= 2B(J+1)
L. Fortunato
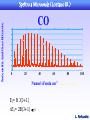
Intensità /unità arbitrarie
Spettro a Microonde (Lontano IR )
CO
0
20
40
60
80
100
Numeri d’onda cm-1
EJ= B J(J+1)
EJ= 2B(J+1)
L. Fortunato
Spectrum Generating Algebra (SGA)
When, in general, one can write an hamiltonian
H= E0 + ckXk + cklXk Xl +…
with
Xk G
as a polynomial in the elements of an algebra
then G is called spectrum generating algebra (SGA)
for H, because it is always possible to diagonalize
(numerically) H in the ONC basis labelled by all the
quantum numbers of a Complete Set of Commuting
Operators (CSCO) of any of the possible chains of
subalgebras of G G’ G’’ …
Once the action of the Xk on | is given, then one
can calculate the matrix elements |H|’
L. Fortunato
Example of SGA
The non-compact algebra SO(2,1) can be realized
with the following differential operators:
Z1=p2
Z2=r2
Z3= k(r·p + p·r)
These operators close under commutation with the
structure constants typical of the SO(2,1) algebra.
Once the action of the Zk on some | is given,
then one can calculate the matrix elements
|H|’ of hamiltonians, for example the
harmonic oscillator :
H = ½p2 + ½r2
(a part from some constants)
L. Fortunato
Dynamical Symmetry
In some cases
H= E0 + ckXk + cklXk Xl +…
with
Xk G
we have only some terms that correspond to invariant
operators of the algebras in the chain:
G G’ G’’ …
C C’ C’’
chain of subalgebras
(one or more for each subalgebra)
H= E0 + aC + a’C’ +a’’C’’ +…
in these cases we speak of a dynamical symmetry and
we have immediately (NO NEED FOR CALCULATIONS)
E= E0 + aC + a’ C’ +a’’ C’’ +…
L. Fortunato
Subalgebra chains: just as an example
Use in the IBM in nuclear physics
The number of possible chains grows with the
dimensions of the algebra. It might get really
complicated...
L. Fortunato
Consequences of a DS -1
1) All the states are soluble and we have analytic
expressions for energy and other observables
E= E0 + aC + a’ C’ +a’’ C’’ +…
2) All the states are characterized by quantum numbers
that “label” the irreducible representations (IRREPS) of
the chain of subalgebras
|12...n
3) The structure of the wavefunctions is dictated by
symmetry and it’s independent from the details of the
hamiltonian
L. Fortunato
Consequences of DS -2
Assume that H commutes with a set of operators
that form a given Lie algebra:
If | is eigenstate of H, then
also gi| is an eigenstate of H and we have
degeneration.
At the very origin of degeneration there is a conserved
quantity, an invariant, that is the Casimir operator of
some group.
L. Fortunato
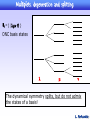
Multiplets, degeneration and splitting.
= { | lm }
ONC basis states
l
m
The dynamical symmetry splits, but do not admix
the states of a basis!
L. Fortunato
Magnetic Degeneration
M= +Jz
J2
M= -Jz
J1
O(3)
O(2)
States with a definite total angular momentum contain
a multiplet of substates with different third component:
these are called magnetic substates because can be
separated with a magnetic field (Zeeman effect)
Said another way, the magnetic interaction -mB
breaks the symmetry of the hamiltonian (Zeeman)
L. Fortunato
Not easy to digest…let’s go through it once again
D o th e ir c o m m u ta to rs c lo s e ?
[X i,X j]= X k
X i i= 1 ,...,n
o p e ra to rs
C a n y o u s o lv e
th e b ra n c h in g
p ro b le m ?
C h a in o f
n e s te d L ie
a lg e b ra s
If y e s
L ie A lg e b ra
o f so m e r a n k
(g e n e ra to rs)
so ( 3 ) m u st b e
co n ta in e d a s a
su b a lg e b r a
a ll cla ssifie d
kn o w n p r o p e r tie s:
- in va r ia n t o p .
- m a tr ix e le m e n ts
C a n H c a n b e e x p re s s e d
a s a lin .c o m b . o f C a s im ir
o p e ra to rs o f th e c h a in ?
C a n H c a n b e e x p re s s e d
in te rm s o f th e g e n e ra to rs ?
If y e s
T h e m a trix e le m e n ts o f
th e h a m ilto n a in c a n b e
c a lc u la te d a n d th e n H
c a n b e d ia g o n a liz e d
S p e c tru m g e n e ra tin g a lg e b ra
If y e s
H is a lre a d y d ia g o n a l in
th e O .N . b a s is d e fin e d
b y th e c h a in . S p e c tru m
c a n b e re a d o ff d ire c tly
D y n a m ic a l S y m m e tr y
L. Fortunato
Example: hydrogen atom so(4)
The states of the hamiltonian of the H atom are
clearly invariant with respect to SO(3), but…
L. Fortunato
Further degeneration
The spectrum shows a further degeneration in .
Where does it come from ?
Degeneration Conserved Quantity
Runge-Lenz vector:
[H,A]=0
there’s a larger symm.
group that contains both
L and A
so(4) so(3) so(3)
L. Fortunato
L. Fortunato
Other important dynamical Symmetries
From R.Bijker
L. Fortunato
The vibron model , U(4) diatomic molecules
Diatomic Molecules
•
Dipolar interaction N = 3
•
Spectrum Generating Algebra: U(4)
•
Vibron Model
F. Iachello. Chem. Phys. Lett. 78 581 (1981)
F. Iachello and R.D.Levine, book, “Algebraic theory of molecules”
L. Fortunato
Definitions:
“Elementary” bosons (IBM building blocks):
b , b †
with =1,…,4
b1= s
b2,…,4= pm
One constructs the u(4) algebra by taking bilinear
operators:
Such that they close into u(4):
[Gr , Gs] = ct Gt
L. Fortunato
Connection with important physical operators
Dipole
From the book :
F.Iachello & R.D.Levine «Algebraic theory of molecules»
Oxford Univ. Press 1995
L. Fortunato
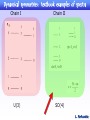
Dynamical symmetries: Chains I & II
I. Non-rigid molecule
(or soft)
II. Rigid molecule
L. Fortunato
Dynamical symmetries: textbook examples of spectra
Chain I
U(3)
Chain II
SO(4)
L. Fortunato
Application to H2 molecular states
Figures from A.Frank and P.van Isacker «Symmetry methods in molecules and nuclei»
Little discrepancies are explained because
this has been fitted with pure SO(4)
dyn.symm. and no Dunham
Ideally a mixture with U(3) should be used:
H = H[U(3)] + (1-) H[SO(4)]
Needs powerpoint to see animation
L. Fortunato
Message to be taken with you
• Some simple models are “naturally” written in terms
of creation and annihilation operators.
• To them we can always associate an algebra that
brings with itself a dynamical symmetry.
• By knowing how to deal mathematically with the
algebra one can get analytic solutions that can be
compared with experimental data (not only: you can
get also new, unexpected solutions!)
• The algebra naturally entails quantum numbers
(=classification), selection rules (= explain some weird
observations).
• The algebra gives a conceptual frame and might give
hints on new physics!!
L. Fortunato
References
• F. Iachello. Chem. Phys. Lett. 78 581 (1981)
• F. Iachello and R.D.Levine, « Algebraic theory of molecules »
• A.Frank and P.van Isacker «Symmetry methods in molecules
and nuclei» SyG editores
• S. Oss, Advances in chemical physics 93, 455-647
• F. Iachello, S.Oss, Chemical physics letters 205 (2-3), 285-289
• F. Pérez-Bernal and L.F., Physics Letters A 376 (2012) 236–244
• L.F. and F. Pérez-Bernal, Phys.Rev. A 94 (2016) 032508
L. Fortunato
Back-up slides
L. Fortunato
Casimir Operators and Rank
For each algebra one can
costruct a set of operators,
called Casimir operators or
invariants, C, such that
[C, Xi]=0 , Xi G
Hendrik Casimir (1909-2000) dutch physicist
The number of independent invariants is called rank of
the algebra, namely #C.
The order is the number of operators (generators) that
form the algebra, namely #Xi G.
L. Fortunato
Intensities in U(4) vibron model
From A.Frank and P.van Isacker book:
«Symmetry methods in Molecules and Nuclei»
L. Fortunato
Fisica Molecolare:
acetilene C2H2
F. Pérez-Bernal and L.F.
Physics Letters A
376 (2012) 236–244
L. Fortunato