* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Flux of an Electric Field - Erwin Sitompul
Survey
Document related concepts
Condensed matter physics wikipedia , lookup
Photon polarization wikipedia , lookup
Four-vector wikipedia , lookup
Electromagnetism wikipedia , lookup
Maxwell's equations wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Lorentz force wikipedia , lookup
Time in physics wikipedia , lookup
Chien-Shiung Wu wikipedia , lookup
Electric charge wikipedia , lookup
Field (physics) wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Transcript
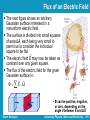
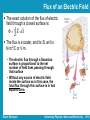
Lecture 8 Ch23. Finding the Electric Field – II University Physics: Waves and Electricity Dr.-Ing. Erwin Sitompul http://zitompul.wordpress.com Homework 6: Three Particles Three particles are fixed in place and have charges q1 = q2 = +p and q3 = +2p. Distance a = 6 μm. What are the magnitude and direction of the net electric field at point P due to the particles? p 1.602 1019 C e 1.602 1019 C Erwin Sitompul University Physics: Wave and Electricity 8/2 Solution of Homework 6: Three Particles EP ,net E1 E2 E3 E2 E3 E1 E1 E2 0 EP ,net E3 k EP ,net r3 P 12 aˆi 12 aˆj r3P 12 2a r rˆ3 P 3 P 12 2iˆ 12 2jˆ r3 P cos ˆi sin ˆj 45 Erwin Sitompul • Both fields cancel one another q3 r3 P r̂ 2 3P (2 1.602 1019 ) 8.99 10 1 ( 2 2(6 106 ))2 9 160 N C • Magnitude EP ,net 45 • Direction University Physics: Wave and Electricity 8/3 The Electric Field → The calculation of the electric field E can be simplified by using→symmetry to discard the perpendicular components of the dE vectors. For certain charge distributions involving symmetry, we can simplify even more by using a law called Gauss’ law, developed by German mathematician and physicist Carl Friedrich Gauss (1777–1855). → Instead of considering dE in a given charge distribution, Gauss’ law considers a hypothetical (imaginary) closed surface enclosing the charge distribution. Gauss’ law relates the electric fields at points on a closed Gaussian surface to the net charge enclosed by that surface. Erwin Sitompul University Physics: Wave and Electricity 8/4 Flux → Suppose that a wide airstream flows with uniform velocity v flows through a small square loop of area A. Let Φ represent the volume flow rate (volume per unit time) at which air flows through the loop. → Φ depends on the angle θ between v and the plane of the loop. A A rˆN Erwin Sitompul • Unit vector pointing to the normal direction of the plane University Physics: Wave and Electricity 8/5 Flux → If v is perpendicular to the plane (or parallel to the plane’s direction), the rate Φ is equal to vA. → If v is parallel to the plane (or perpendicular to the plane’s direction), no air moves through the loop, so Φ is zero. For an intermediate angle θ, the rate of volume flow through the loop is: (v cos ) A v A This rate of flow through an area is an example of a flux. The flux can be interpreted as the flow of the velocity field through the loop. Erwin Sitompul University Physics: Wave and Electricity 8/6 Flashback: Multiplying Vectors The Scalar Product → → →→ The scalar product of the vector a and b is written as a·b and defined to be: a b ab cos →→ Because of the notation, a·b is also known as the dot product and is spoken as “a dot b.” → → If a is perpendicular to b, means Φ = 90°, then the dot product is equal to zero. → → If a is parallel to b, means Φ = 0, then the dot product is equal to ab. Erwin Sitompul University Physics: Wave and Electricity 8/7 Flashback: Multiplying Vectors The dot product can be regarded as the product of the magnitude of the first vector and the projection magnitude of the second vector on the first vector a b ab cos (a cos )(b) (a)(b cos ) Erwin Sitompul University Physics: Wave and Electricity 8/8 Flashback: Multiplying Vectors When two vectors are in unit vector notation, their dot product can be written as ˆ (b ˆi b ˆj b k) ˆ a b (ax ˆi a y ˆj az k) x y z axbx a y by az bz ˆi ˆj kˆ î 1 0 0 ĵ 0 1 0 k̂ 0 0 1 Erwin Sitompul University Physics: Wave and Electricity 8/9 Flashback: Multiplying Vectors → ^ → ^ ^ ^ What is the angle Φ between a = 3i – 4j and b = –2i + 3k ? z Solution: a b ab cos 3 a 3 (4) 5 2 2 –4 b –2 y a b (2) 2 32 3.606 3 ˆ a b (3iˆ 4ˆj) (2iˆ 3k) ˆ 2i) ˆ (3i)( 6 x ˆi ˆj kˆ î 1 0 0 ĵ 0 1 0 k̂ 0 0 1 6 (5)(3.606) cos 6 1 cos 109.438 (5)(3.606) Erwin Sitompul University Physics: Wave and Electricity 8/10 Flux of an Electric Field The next figure shows an arbitrary Gaussian surface immersed in a nonuniform electric field. The surface is divided into small squares of area ΔA, each being very small to permit us to consider the individual square to be flat. → The electric field E may now be taken as constant over any given square. The flux of the electric field for the given Gaussian surface is: E A • Φ can be positive, negative, or zero, depending → on the → angle θ between E and ΔA Erwin Sitompul University Physics: Wave and Electricity 8/11 Flux of an Electric Field The exact solution of the flux of electric field through a closed surface is: E dA The flux is a scalar, and its Si unit is Nm2/C or Vm. • The electric flux through a Gaussian surface is proportional to the net number of field lines passing through that surface • Without any source of electric field inside the surface as in this case, the total flux through this surface is in fact equal to zero Erwin Sitompul University Physics: Wave and Electricity 8/12 Checkpoint The figure below shows a Gaussian cube of face area A immersed in a uniform electric field E that has the positive direction of the z axis. In terms of E and A, determine the flux flowing through: (a) the front face (xy plane) Φ = +EA (b) the rear face Φ = –EA (c) the top face Φ=0 (d) the whole cube Φ=0 Erwin Sitompul University Physics: Wave and Electricity 8/13 Example: Flux of an Electric Field In a three-dimensional space, a homogenous electric field of 10 V/m is directed down to the negative z direction. Calculate the flux flowing through: (a) the square ABCD (xy plane) z E (b) the rectangular AEFG (xz plane) 3 (a) E 10kˆ V m AABCD 4kˆ m2 ABCD E AABCD ˆ (4k) ˆ (10k) 40 Vm (b) AAEFG 6jˆ m 2 1 F A 2 AEFG E AAEFG ˆ (6ˆj) (10k) 0 G 1 0 B 1 2 3 y 2 3 D C x E Erwin Sitompul University Physics: Wave and Electricity 8/14 Homework 7 (a) The rectangle ABCD is defined by its corner points of A(2,0,0), B(0,3,0), C(0,3,2.5), and D(2,0,2.5). Draw a sketch of the rectangular. → ^ ^ (b) Given an electric field of E = –2i + 6j V/m, draw the electric field on the sketch from part (a). (c) Determine the number of flux crossing the area of the rectangular ABCD. Erwin Sitompul University Physics: Wave and Electricity 8/15 Homework 7 New (a) The triangle FGH is defined by its corner points of F(2,0,0), G(0,3,0), and H(0,0,4). Draw a sketch of the rectangular. → ^ ^ (b) Given an electric field of E = –2i + 6j V/m, draw the electric field on the sketch from part (a). (c) Determine the number of flux crossing the area of the triangle FGH. Erwin Sitompul University Physics: Wave and Electricity 8/16