* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download ch09
N-body problem wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Old quantum theory wikipedia , lookup
Center of mass wikipedia , lookup
Jerk (physics) wikipedia , lookup
Fictitious force wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Mass versus weight wikipedia , lookup
Rigid rotor wikipedia , lookup
Classical mechanics wikipedia , lookup
Virtual work wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Moment of inertia wikipedia , lookup
Centripetal force wikipedia , lookup
Photon polarization wikipedia , lookup
Angular momentum operator wikipedia , lookup
Hunting oscillation wikipedia , lookup
Angular momentum wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Equations of motion wikipedia , lookup
Work (physics) wikipedia , lookup
Classical central-force problem wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
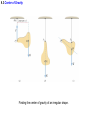
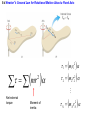
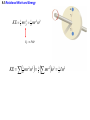
Chapter 9 Rotational Dynamics 9.1 The Action of Forces and Torques on Rigid Objects In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 9.1 The Action of Forces and Torques on Rigid Objects According to Newton’s second law, a net force causes an object to have an acceleration. What causes an object to have an angular acceleration? TORQUE 9.1 The Action of Forces and Torques on Rigid Objects The amount of torque depends on where and in what direction the force is applied, as well as the location of the axis of rotation. 9.1 The Action of Forces and Torques on Rigid Objects DEFINITION OF TORQUE Magnitude of Torque = (Magnitude of the force) x (Lever arm) F Direction: The torque is positive when the force tends to produce a counterclockwise rotation about the axis. SI Unit of Torque: newton x meter (N·m) 9.1 The Action of Forces and Torques on Rigid Objects Example 2 The Achilles Tendon The tendon exerts a force of magnitude 790 N. Determine the torque (magnitude and direction) of this force about the ankle joint. 9.1 The Action of Forces and Torques on Rigid Objects F cos 55 3.6 10 2 m 790 N 720 N 3.6 10 2 m cos 55 15 N m 9.2 Rigid Objects in Equilibrium If a rigid body is in equilibrium, neither its linear motion nor its rotational motion changes. ax a y 0 F x 0 0 F y 0 0 9.2 Rigid Objects in Equilibrium EQUILIBRIUM OF A RIGID BODY A rigid body is in equilibrium if it has zero translational acceleration and zero angular acceleration. In equilibrium, the sum of the externally applied forces is zero, and the sum of the externally applied torques is zero. F x 0 F y 0 0 9.2 Rigid Objects in Equilibrium Reasoning Strategy 1. Select the object to which the equations for equilibrium are to be applied. 2. Draw a free-body diagram that shows all of the external forces acting on the object. 3. Choose a convenient set of x, y axes and resolve all forces into components that lie along these axes. 4. Apply the equations that specify the balance of forces at equilibrium. (Set the net force in the x and y directions equal to zero.) 5. Select a convenient axis of rotation. Set the sum of the torques about this axis equal to zero. 6. Solve the equations for the desired unknown quantities. 9.2 Rigid Objects in Equilibrium Example 3 A Diving Board A woman whose weight is 530 N is poised at the right end of a diving board with length 3.90 m. The board has negligible weight and is supported by a fulcrum 1.40 m away from the left end. Find the forces that the bolt and the fulcrum exert on the board. 9.2 Rigid Objects in Equilibrium F 2 2 W W 0 W W F2 2 F2 530 N 3.90 m 1480 N 1.40 m 9.2 Rigid Objects in Equilibrium F y F1 F2 W 0 F1 1480 N 530 N 0 F1 950 N 9.2 Rigid Objects in Equilibrium Example 5 Bodybuilding The arm is horizontal and weighs 31.0 N. The deltoid muscle can supply 1840 N of force. What is the weight of the heaviest dumbell he can hold? 9.2 Rigid Objects in Equilibrium W a a Wd d M M 0 M 0.150 msin 13.0 9.2 Rigid Objects in Equilibrium Wa a M M Wd d 31.0 N 0.280 m 1840 N 0.150 m sin 13.0 86.1 N 0.620 m 9.3 Center of Gravity DEFINITION OF CENTER OF GRAVITY The center of gravity of a rigid body is the point at which its weight can be considered to act when the torque due to the weight is being calculated. 9.3 Center of Gravity When an object has a symmetrical shape and its weight is distributed uniformly, the center of gravity lies at its geometrical center. 9.3 Center of Gravity W1 x1 W2 x2 xcg W1 W2 9.3 Center of Gravity Example 6 The Center of Gravity of an Arm The horizontal arm is composed of three parts: the upper arm (17 N), the lower arm (11 N), and the hand (4.2 N). Find the center of gravity of the arm relative to the shoulder joint. 9.3 Center of Gravity W1 x1 W2 x2 xcg W1 W2 xcg 17 N 0.13 m 11 N 0.38 m 4.2 N 0.61 m 0.28 m 17 N 11 N 4.2 N 9.3 Center of Gravity Conceptual Example 7 Overloading a Cargo Plane This accident occurred because the plane was overloaded toward the rear. How did a shift in the center of gravity of the plane cause the accident? 9.3 Center of Gravity Finding the center of gravity of an irregular shape. 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis FT maT FT r aT r mr 2 Moment of Inertia, I 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis mr 2 Net external torque Moment of inertia 1 m1r12 2 m r 2 2 2 N mN rN2 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis ROTATIONAL ANALOG OF NEWTON’S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS Moment of Angular Net external torque inertia accelerati on I Requirement: Angular acceleration must be expressed in radians/s2. I mr 2 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis Example 9 The Moment of Inertial Depends on Where the Axis Is. Two particles each have mass and are fixed at the ends of a thin rigid rod. The length of the rod is L. Find the moment of inertia when this object rotates relative to an axis that is perpendicular to the rod at (a) one end and (b) the center. 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis (a) I mr 2 m1r12 m2 r22 m0 mL 2 m1 m2 m I mL 2 2 r1 0 r2 L 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis (b) I mr 2 m1r12 m2 r22 mL 2 2 mL 2 2 m1 m2 m I mL 1 2 2 r1 L 2 r2 L 2 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis Example 12 Hoisting a Crate The combined moment of inertia of the dual pulley is 50.0 kg·m2. The crate weighs 4420 N. A tension of 2150 N is maintained in the cable attached to the motor. Find the angular acceleration of the dual pulley. 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis equal F T y 2 mg may a y 2 T T2 mg may 1 1 T2 2 I 9.4 Newton’s Second Law for Rotational Motion About a Fixed Axis T1 1 mg may 2 I a y 2 T11 mg m 2 2 I T1 1 mg 2 I m 22 2150 N 0.600 m 451 kg 9.80 m s 2 0.200 m 6.3 rad 2 2 46.0 kg m 451 kg 0.200 m s2 9.5 Rotational Work and Energy s r W Fs Fr Fr W 9.5 Rotational Work and Energy DEFINITION OF ROTATIONAL WORK The rotational work done by a constant torque in turning an object through an angle is WR Requirement: The angle must be expressed in radians. SI Unit of Rotational Work: joule (J) 9.5 Rotational Work and Energy KE 12 mvT2 12 mr 2 2 vT r mr KE 12 mr 2 2 12 2 2 12 I 2 9.5 Rotational Work and Energy DEFINITION OF ROTATIONAL KINETIC ENERGY The rotational kinetic energy of a rigid rotating object is KER 12 I 2 Requirement: The angular speed must be expressed in rad/s. SI Unit of Rotational Kinetic Energy: joule (J) 9.5 Rotational Work and Energy Example 13 Rolling Cylinders A thin-walled hollow cylinder (mass = mh, radius = rh) and a solid cylinder (mass = ms, radius = rs) start from rest at the top of an incline. Determine which cylinder has the greatest translational speed upon reaching the bottom. 9.5 Rotational Work and Energy E 12 mv2 12 I 2 mgh ENERGY CONSERVATION 1 2 1 2 mv2f 12 I 2f mghf 12 mvi2 12 Ii2 mghi mv2f 12 I 2f mghi f vf r 9.5 Rotational Work and Energy 1 2 mv2f 12 I v 2f r 2 mghi 2mgho vf m I r2 The cylinder with the smaller moment of inertia will have a greater final translational speed. 9.6 Angular Momentum DEFINITION OF ANGULAR MOMENTUM The angular momentum L of a body rotating about a fixed axis is the product of the body’s moment of inertia and its angular velocity with respect to that axis: L I Requirement: The angular speed must be expressed in rad/s. SI Unit of Angular Momentum: kg·m2/s 9.6 Angular Momentum PRINCIPLE OF CONSERVATION OFANGULAR MOMENTUM The angular momentum of a system remains constant (is conserved) if the net external torque acting on the system is zero. 9.6 Angular Momentum Conceptual Example 14 A Spinning Skater An ice skater is spinning with both arms and a leg outstretched. She pulls her arms and leg inward and her spinning motion changes dramatically. Use the principle of conservation of angular momentum to explain how and why her spinning motion changes. 9.6 Angular Momentum Example 15 A Satellite in an Elliptical Orbit An artificial satellite is placed in an elliptical orbit about the earth. Its point of closest approach is 8.37x106m from the center of the earth, and its point of greatest distance is 25.1x106m from the center of the earth. The speed of the satellite at the perigee is 8450 m/s. Find the speed at the apogee. 9.6 Angular Momentum L I angular momentum conservation I AA I PP I mr 2 v r vA 2 vP mr mrP rA rP 2 A 9.6 Angular Momentum vA 2 vP mr mrP rA rP 2 A rA v A rP vP rP vP 8.37 106 m 8450 m s vA 2820 m s 6 rA 25.110 m