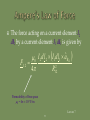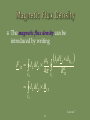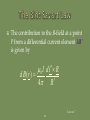* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download magnetic dipole
Geomagnetic storm wikipedia , lookup
Edward Sabine wikipedia , lookup
Skin effect wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
Electric dipole moment wikipedia , lookup
Superconducting magnet wikipedia , lookup
Magnetic stripe card wikipedia , lookup
Electromotive force wikipedia , lookup
Maxwell's equations wikipedia , lookup
Giant magnetoresistance wikipedia , lookup
Magnetometer wikipedia , lookup
Magnetic field wikipedia , lookup
Magnetic nanoparticles wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Earth's magnetic field wikipedia , lookup
Electromagnetism wikipedia , lookup
Mathematical descriptions of the electromagnetic field wikipedia , lookup
Magnetotactic bacteria wikipedia , lookup
Electromagnetic field wikipedia , lookup
Magnetic monopole wikipedia , lookup
Magnetotellurics wikipedia , lookup
Magnetoreception wikipedia , lookup
Multiferroics wikipedia , lookup
Electromagnet wikipedia , lookup
Magnetochemistry wikipedia , lookup
Ferromagnetism wikipedia , lookup
History of geomagnetism wikipedia , lookup
Faraday paradox wikipedia , lookup
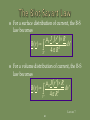
Lecture 7: Magnetostatics: Ampere’s Law Of Force; Magnetic Flux Density; Lorentz Force; Biot-savart Law; Applications Of Ampere’s Law In Integral Form; Vector Magnetic Potential; Magnetic Dipole; Magnetic Flux Lecture 7 1 To begin our study of magnetostatics with Ampere’s law of force; magnetic flux density; Lorentz force; Biot-Savart law; applications of Ampere’s law in integral form; vector magnetic potential; magnetic dipole; magnetic flux. Lecture 7 2 Fundamental laws of classical electromagnetics Special cases Electrostatics Statics: Input from other disciplines Maxwell’s equations Magnetostatics Electromagnetic waves 0 t Geometric Optics Transmission Line Theory Circuit Theory Kirchoff’s Laws d Lecture 7 3 Magnetostatics is the branch of electromagnetics dealing with the effects of electric charges in steady motion (i.e, steady current or DC). The fundamental law of magnetostatics is Ampere’s law of force. Ampere’s law of force is analogous to Coulomb’s law in electrostatics. Lecture 7 4 In magnetostatics, the magnetic field is produced by steady currents. The magnetostatic field does not allow for inductive coupling between circuits coupling between electric and magnetic fields Lecture 7 5 Ampere’s law of force is the “law of action” between current carrying circuits. Ampere’s law of force gives the magnetic force between two current carrying circuits in an otherwise empty universe. Ampere’s law of force involves complete circuits since current must flow in closed loops. Lecture 7 6 Experimental facts: Two parallel wires carrying current in the same direction attract. Two parallel wires carrying current in the opposite directions repel. F21 F12 I1 F21 I2 F12 I1 I2 Lecture 7 7 Experimental facts: A short currentcarrying wire oriented perpendicular to a long currentcarrying wire experiences no force. F12 = 0 I2 I1 Lecture 7 8 Experimental facts: The magnitude of the force is inversely proportional to the distance squared. The magnitude of the force is proportional to the product of the currents carried by the two wires. Lecture 7 9 The direction of the force established by the experimental facts can be mathematically represented by unit vector in direction of current I2 unit vector in direction of current I1 aˆ F1 2 aˆ 2 aˆ1 aˆ R1 2 unit vector in direction of force on I2 due to I1 unit vector in direction of I2 from I1 Lecture 7 10 The force acting on a current element I2 dl2 by a current element I1 dl1 is given by 0 I 2 d l 2 I1d l 1 aˆ R F 12 2 4 R12 12 Permeability of free space 0 = 4 10-7 F/m Lecture 7 11 The total force acting on a circuit C2 having a current I2 by a circuit C1 having current I1 is given by 0 I1 I 2 F 12 4 C 2 C1 d l 2 d l 1 aˆ R1 2 2 12 R Lecture 7 12 The force on C1 due to C2 is equal in magnitude but opposite in direction to the force on C2 due to C1. F 21 F 12 Lecture 7 13 Ampere’s force law describes an “action at a distance” analogous to Coulomb’s law. In Coulomb’s law, it was useful to introduce the concept of an electric field to describe the interaction between the charges. In Ampere’s law, we can define an appropriate field that may be regarded as the means by which currents exert force Lecture 7 on each other. 14 The magnetic flux density can be introduced by writing 0 F 12 I 2 d l 2 4 C 2 C1 I d l 1 1 aˆ R1 2 2 12 R I 2 d l 2 B12 C2 Lecture 7 15 where 0 B12 4 I1d l 1 aˆ R1 2 C1 2 12 R the magnetic flux density at the location of dl2 due to the current I1 in C1 Lecture 7 16 Suppose that an infinitesimal current element Idl is immersed in a region of magnetic flux density B. The current element experiences a force dF given by d F Id l B Lecture 7 17 The total force exerted on a circuit C carrying current I that is immersed in a magnetic flux density B is given by F I dl B C Lecture 7 18 A moving point charge placed in a magnetic field experiences a force given F byQ v B Id l Q v m Q v B The force experienced by the point charge is in the direction into the paper. Lecture 7 19 If a point charge is moving in a region where both electric and magnetic fields exist, then it experiences a total force given by F F e F m q E v B The Lorentz force equation is useful for determining the equation of motion for electrons in electromagnetic deflection Lecture 7 systems such as CRTs. 20 The Biot-Savart law gives us the B-field arising at a specified point P from a given current distribution. It is a fundamental law of magnetostatics. Lecture 7 21 The contribution to the B-field at a point P from a differential current element Idl’ is given by 0 I d l R d B (r ) 3 4 R Lecture 7 22 P R Id l r r Lecture 7 23 The total magnetic flux at the point P due to the entire circuit C is given by 0 I d l R B (r ) 3 4 R C Lecture 7 24 Line current density (current) - occurs for infinitesimally thin filamentary bodies (i.e., wires of negligible diameter). Surface current density (current per unit width) - occurs when body is perfectly conducting. Volume current density (current per unit cross sectional area) - most general. Lecture 7 25 For a surface distribution of current, the B-S law becomes 0 J s r R B (r ) ds 3 4 R S For a volume distribution of current, the B-S law becomes 0 J r R B (r ) dv 3 4 R V Lecture 7 26 Ampere’s Circuital Law in integral form states that “the circulation of the magnetic flux density in free space is proportional to the total current through the surface bounding the path over which the circulation is computed.” B d l I 0 encl C Lecture 7 27 By convention, dS is taken to be in the direction defined by the right-hand rule applied to dl. dl dS S I encl J d s S Since volume current density is the most general, we can write Iencl in this way. Lecture 7 28 Just as Gauss’s law follows from Coulomb’s law, so Ampere’s circuital law follows from Ampere’s force law. Just as Gauss’s law can be used to derive the electrostatic field from symmetric charge distributions, so Ampere’s law can be used to derive the magnetostatic field from symmetric current distributions. Lecture 7 29 Ampere’s law in integral form is an integral equation for the unknown magnetic flux density resulting from a given current distribution. B d l I 0 encl C known unknown Lecture 7 30 In general, solutions to integral equations must be obtained using numerical techniques. However, for certain symmetric current distributions closed form solutions to Ampere’s law can be obtained. Lecture 7 31 Closed form solution to Ampere’s law relies on our ability to construct a suitable family of Amperian paths. An Amperian path is a closed contour to which the magnetic flux density is tangential and over which equal to a constant value. Lecture 7 32 Consider an infinite line current along the z-axis carrying current in the +zdirection: I Lecture 7 33 (1) Assume from symmetry and the righthand rule the form of the field B aˆ B (2) Construct a family of Amperian paths circles of radius where Lecture 7 34 (3) Evaluate the total current passing through the surface bounded by the Amperian path I encl J d s S Lecture 7 35 y Amperian path x I I encl I Lecture 7 36 (4) For each Amperian path, evaluate the integral length B d l Bl C magnitude of B on Amperian path. of Amperian path. B d l B 2 C Lecture 7 37 (5) Solve for B on each Amperian path 0 I encl B l 0 I B aˆ 2 Lecture 7 38 B dl Bd s C S 0 I encl 0 J d s S Because the above must hold for any surface S, we must have Differential form of Ampere’s Law B 0 J Lecture 7 39 Ampere’s law in differential form implies that the B-field is conservative outside of regions where current is flowing. Lecture 7 40 Ampere’s law in differential form B 0 J No isolated magnetic charges B 0 B is solenoidal Lecture 7 41 Vector identity: “the divergence of the curl of any vector field is identically zero.” A 0 Corollary: “If the divergence of a vector field is identically zero, then that vector field can be written as the curl of some vector potential field.” Lecture 7 42 Since the magnetic flux density is solenoidal, it can be written as the curl of a vector field called the vector magnetic potential. B 0 B A Lecture 7 43 The general form of the B-S law is 0 J r R B (r ) dv 3 4 R V Note that R 1 3 R R Lecture 7 44 Furthermore, note that the del operator operates only on the unprimed coordinates so that J r R 1 J r 3 R R 1 J r R J r R Lecture 7 45 Hence, we have 0 B r 4 J r d v V R Ar Lecture 7 46 For a surface distribution of current, the vector magnetic potential is given by 0 A( r ) 4 J s r S R ds For a line current, the vector magnetic potential is given by 0 I d l A( r ) 4 L R Lecture 7 47 In some cases, it is easier to evaluate the vector magnetic potential and then use B = A, rather than to use the B-S law to directly find B. In some ways, the vector magnetic potential A is analogous to the scalar electric potential V. Lecture 7 48 In classical physics, the vector magnetic potential is viewed as an auxiliary function with no physical meaning. However, there are phenomena in quantum mechanics that suggest that the vector magnetic potential is a real (i.e., measurable) field. Lecture 7 49 A magnetic dipole comprises a small current carrying loop. The point charge (charge monopole) is the simplest source of electrostatic field. The magnetic dipole is the simplest source of magnetostatic field. There is no such thing as a magnetic monopole (at least as far as classical physics is concerned). Lecture 7 50 The magnetic dipole is analogous to the electric dipole. Just as the electric dipole is useful in helping us to understand the behavior of dielectric materials, so the magnetic dipole is useful in helping us to understand the behavior of magnetic materials. Lecture 7 51 Consider a small circular loop of radius b carrying a steady current I. Assume that the wire radius has a negligible crosssection. y x b Lecture 7 52 The vector magnetic potential is evaluated for R >> b as 0 I 2 aˆ bd A(r ) R 4 0 0 Ib 2 1 b sin cos d aˆ x sin aˆ y cos 2 r 4 0 r 0 Ib b sin aˆ x sin aˆ y cos r2 4 0 Ib 2 sin aˆ 2 4 r Lecture 7 53 The magnetic flux density is evaluated for R >> b as 0 2 ˆ ˆ B A I b a 2 cos a r sin 3 4 r Lecture 7 54 Recall electric dipole p aˆ r 2 cos aˆ sin E 3 4 0 r p electric dipole moment Qd The electric field due to the electric charge dipole and the magnetic field due to the magnetic dipole are dual quantities. Lecture 7 55 The magnetic dipole moment can be defined as 2 m aˆ z I b Direction of the dipole moment is determined by the direction of current using the right-hand rule. Magnitude of the dipole moment is the product of the current and the area of the loop. Lecture 7 56 We can write the vector magnetic potential in terms of the magnetic dipole moment as 0 m sin 0 m aˆ r A aˆ 2 2 4 r 4 r We can write the B field in terms of the magnetic dipole moment as 0 0 1 B m aˆ r 2 cos aˆ sin m 3 4 r 4 r Lecture 7 57 The B-field is solenoidal, i.e. the divergence of the B-field is identically equal to zero: B 0 Physically, this means that magnetic charges (monopoles) do not exist. A magnetic charge can be viewed as an isolated magnetic pole. Lecture 7 58 No matter how small the magnetic is divided, it always has a north pole and a south pole. The elementary source of magnetic field is a magnetic dipole. N N S S N S N I S Lecture 7 59 The magnetic flux crossing an open surface S is given by B Bds Wb S C S Wb/m2 Lecture 7 60 From the divergence theorem, we have B 0 B dv 0 B d s 0 V S Hence, the net magnetic flux leaving any closed surface is zero. This is another manifestation of the fact that there are no magnetic charges. Lecture 7 61 The magnetic flux across an open surface may be evaluated in terms of the vector magnetic potential using Stokes’s theorem: B d s A d s S S Adl C Lecture 7 62