Download Power Flow Analysis

Power Flow Analysis
Ian A. Hiskens
Department of Electrical and Computer Engineering
University of Wisconsin - Madison
November 6, 2003
1
Introduction
1.1
Background
Successful operation of electrical systems requires that:
• generation must supply the demand (load) plus the losses,
• bus voltage magnitudes must remain close to rated values,
• generators must operate within specified real and reactive power limits,
• transmission lines and transformers should not be overloaded for long periods.
Therefore it is important that voltages and power flows in an electrical system can be determined for a given set of loading and operating conditions. This is known as the power flow
problem. Power flow analysis is used extensively in the planning, design and operation of
electrical systems.
In power flow analysis, it is normal to assume that the system is balanced and that the
network is composed of constant, linear, lumped-parameter branches. (In the most basic form
of the power flow, transformer taps are assumed to be fixed. This assumption is relaxed in
commercial power flows though.) Therefore nodal analysis is generally used to describe the
network. However, because the injection/demand at busbars is generally specified in terms of
real and reactive power, the overall problem is nonlinear. Accordingly, the power flow problem
is a set of simultaneous nonlinear algebraic equations. Numerical techniques are required to
solve this set of equations.
1.2
Constraints at Nodes
Four variables are associated with each node:
• bus voltage magnitude (V ),
• voltage angle (θ),
• real power (P ), and
• reactive power (Q).
1
Also, as we will show later, each node introduces two equations, namely the real and reactive
power balance equations. To obtain (isolated) solutions for a set of simultaneous equations,
it is necessary to have the same number of equations as unknowns. Therefore two of the
variables associated with each bus must be specified, i.e., given fixed values. The other two
variables are free to vary during the solution process.
The traditional way of specifying busbar quantities allows buses to be identified as follows:
P Q Busbar, at which the nett active and reactive powers are specified. The nett power
entering a busbar is the power supplied to the system from a generating source minus
the power consumed by a load at that busbar.
P V Busbar, at which the nett active power is specified, and the voltage magnitude is specified. The nett reactive power is an unknown which is determined as part of the power
flow solution. This type of busbar typically represents a node in the system at which a
synchronous source (generator or compensator) is connected, where the source’s reactive
power output is varied to control the voltage magnitude to a scheduled value.
Slack or Swing Busbar, where the voltage magnitude and angle are specified. Generally
the angle is set to zero. Unlike the other two bus types, which represent physical system
conditions, this busbar type is more a mathematical requirement. It is needed to provide
a ‘reference’ angle to which all other angles are referred. Also, this bus absorbs any real
power mismatch across the system. (Note that it is not possible to specify the nett
active power at all buses in the system, because transmission losses are unknown until
the power flow solution is completed.) Normally there can only be one slack busbar in
the system. It is generally chosen from among the voltage controlled busbars.
Note that even though these bus types are the most common, others are possible, e.g.,
slack buses with constrained reactive power. In fact they are required at times. Also note that
in general transformer taps are not fixed, but vary to regulate bus voltage. This introduces
other bus types. However, so that the important aspects of power flows are clearly highlighted,
only P Q, P V and slack buses will be considered here. Further details of other bus types can
be found in [1].
1.3
Minimum Data Input Requirements for Solution
The minimum data required to fully specify system conditions is:
• Impedances (usually in per-unit) for all series and shunt branches of the transmission
network. Network elements are represented as lumped complex impedances at rated
frequency (e.g. transmission lines, in-phase transformers, series and shunt reactors and
capacitors). Transmission lines with non-negligible charging capacitance are represented
by their simple equivalent π networks.
• Active-power (P Q and P V ) and reactive-power (P Q) busbar generations and loads.
Voltage magnitudes at P V and slack busbars.
1.4
Solution Outputs
Power flow solution typically provides:
2
• Voltage magnitude and angle at each busbar.
• Real and reactive power generation and load at each busbar.
• Power flows and MVA loadings at both ends of each transmission line and transformer.
• Power generation or consumption of each static shunt compensating device.
• Total system losses.
2
Nodal Analysis of the Transmission Network
2.1
Introduction
Conventional power flows assume balanced three-phase networks. Therefore the network
may be represented in single-phase (positive sequence) form. Circuit elements are usually
represented in per-unit by linear lumped complex impedances at rated system frequency,
e.g. in-phase transformers, transmission lines, series and shunt capacitors and reactors. The
transmission line is represented by its equivalent π network. The equations describing the
transmission network are therefore linear.
In theory there are an infinite number of ways of describing analytically an electrical
network; the common factor being that Kirchoff’s current and voltage laws and the voltampere relations of the network branches must be satisfied. In practice, two methods - mesh
(or loop) and nodal analysis - have emerged as the most useful. Of these, the latter has been
found to be much more suitable for power system analysis.
2.2
The Basic Nodal Method
As far as power networks are concerned, the major advantages of the nodal approach may be
listed as follows:
• Data preparation is easy.
• The number of variables and equations is usually less than with the mesh method for
power networks.
• Parallel branches do not increase the number of variables or equations.
• Node voltages are available directly from the solution, and branch currents are easily
calculated.
• Off-nominal transformer taps can easily be represented.
In the application of the nodal method to power system networks, the variables are the
complex node (busbar) voltages and currents, for which some reference must be designated.
In fact, two different references are normally chosen: for voltage magnitudes the reference is
ground, and for voltage angles the reference is chosen as one of the busbar voltage angles,
which is fixed at the value zero (usually). This bus is called the slack (or swing) bus, as
discussed in Section 1.2. A nodal current is the nett current entering (injected into) the
network at a given node, from a source and/or load external to the network. From this
3
I 1(S 1 + E 1I *1)
I 2(S 2 + E 2I *2)
z 12
1
z 10
0
I 3(S 3 + E 3I *3)
z 23
2
+
+
+
E1
z 30
E3
E2
–
–
3
–
Figure 1: Simple network showing nodal quantities
definition a current entering the network (from a source) is positive in sign, while a current
leaving the network (to a load) is negative. The nett nodal injected current is the algebraic
sum of these. Nodal injected powers S = P + jQ are defined similarly. Figure 1 gives a simple
network showing the nodal currents, voltages and powers.
In the nodal method, it is convenient to use branch admittances rather than impedances.
Denoting the voltages of nodes i and k as Ei and Ek respectively, and the admittance of the
branch between them as yik , then the current flowing in this branch from node i to node k is
given by:
(1)
Iik = yik (Ei − Ek )
Let the nodes in the network be numbered 0, 1 · · · n, where 0 designates the reference
node (ground). By Kirchoff’s current law, the injected current Ii must be equal to the sum
of the currents leaving node i, hence:
Ii =
n
Iik =
k=0
n
yik (Ei − Ek )
(2)
k=0
Since E0 = 0 and if the system is linear,
Ii =
n
yik Ei −
k=0
In
Yn1
yik Ek
(3)
k=1
k=i
If this equation is written for all the
the case of a power system network, then
obtained in matrix form as:
 

Y11
I1
 I2   Y21
 

 ..  =  ..
 .   .
n
k=i
nodes except the reference, i.e. for all busbars in
a complete set of equations defining the network is
Y12 · · · Y1n
Y22 · · · Y2n
..
..
.
.
Yn2 · · · Ynn





E1
E2
..
.





En
where
Yii =
n
yik = self admittance of node i
k=0
k=i
Yik = −yik = mutual admittance between nodes i and k
4
(4)
I2
I1
y 12
+
+
y 23
y 13
E1
E3
+
E2
–
–
I3
–
Figure 2: Example of Singular Network
In matrix notation, (4) is simply
I=Y E
(5)
or in summation notation, we have
Ii =
n
Yik Ek
for i = 1, · · · n
(6)
k=1
The nodal admittance matrix in (4) or (5) has a well-defined structure, which makes it
easy to construct. Its properties are as follows:
• Square of order n × n.
• Symmetrical, since Yik = Yki .
• Complex.
• Each off-diagonal element Yik is the negative of the branch admittance between nodes
i and k, and is frequently of value zero.
• Each diagonal element Yii is the sum of the admittances of the branches which terminate
at node i, including branches to ground.
• Very few non-zero mutual admittances exist in practical networks. Therefore matrix Y
is generally highly sparse.
2.3
Conditioning the Y Matrix
The set of equations I = Y E may or may not have a solution. If not, there is generally
a simple physical explanation relating to the formulation of the network description. Any
numerical attempt to solve such equations is bound to break down at some stage of the
process. (In practice this usually results in a finite number being divided by zero.) The
example of Figure 2 illustrates this.
The nodal equations are constructed in the usual way as:
 



−y12
−y13
y12 + y13
E1
I1
 I2  =  −y12
y12 + y23
−y23   E2 
(7)
I3
−y13
−y23
y13 + y23
E3
5
i.e.
I=Y E
Suppose that the injected currents are known, and nodal voltages are unknown. In this case
no solution for the latter is possible. The Y matrix is singular, i.e. it has no inverse. This is
easily detected in this example by noting that the sum of the elements in each row and column
is zero, which is a sufficient condition for singularity. Hence, if it is not possible to express the
voltages in the form E = Y −1 I, it is clearly impossible to solve (7) by any method, whether
involving inversion of Y or otherwise.
The reason is that we are attempting to solve a network whose reference is disconnected,
i.e. there is no effective reference node. Therefore an infinite number of voltage solutions will
satisfy the given injected current values.
However, when a shunt admittance from at least one of the busbars in the network of
Figure 2 is present, the problem of insolubility immediately vanishes (in theory, but not
necessarily in practice). Practical computation cannot be performed with absolute accuracy,
and during a sequence of arithmetic operations, rounding errors due to working with a finite
number of decimal places accumulate. If the problem is well-conditioned and the numerical
solution technique is suitable, these errors remain small and do not mask the eventual results.
If the problem is ill-conditioned, and this usually depends upon the properties of the system
being analysed, any computational errors introduced are likely to become large with respect
to the true solution.
It can be seen intuitively that if a network having zero shunt admittances cannot be solved
when working with absolute computational accuracy, then a network having very small shunt
admittances may well present difficulties when working with limited computational accuracy.
This reasoning provides a key to the practical problems of network (Y matrix) conditioning. A
network with shunt admittances which are small with respect to the other branch admittances
is likely to be ill-conditioned. The conditioning tends to improve with the size of the shunt
admittances, i.e. with the electrical connection between the network busbars and the reference
node.
2.4
The Case Where One Voltage is Known
In power flow studies, it is normal for at least one of the voltages in the network to be
specified, with the current at that busbar being unknown. This immediately alleviates the
problem of needing at least one good connection with ground, because a fixed busbar voltage
can be interpreted as an infinitely strong ground tie. If it is represented as a voltage source
with a series impedance of zero, then when converted to the Norton equivalent, the fictitious
shunt admittance is infinite, as is the injected current. This approach is not computationally
feasible, however.
The usual way to deal with a voltage which is fixed is to effectively eliminate it as a
variable from the nodal equations. For the sake of analytical convenience, let this busbar be
numbered 1 in an n-busbar network. The nodal equations are then
I1 = Y11 E1 + Y12 E2 + · · · Y1n En
I2 = Y21 E1 + Y22 E2 + · · · Y2n En
..
.
6
(8)
In = Yn1 E1 + Yn2 E2 + · · · Ynn En
The terms in E1 on the right-hand side of (8) are known quantities, and as such are
transferred to the left-hand side.
I1 − Y11 E1 = Y12 E2 + · · · Y1n En
I2 − Y21 E1 = Y22 E2 + · · · Y2n En
..
.
(9)
In − Yn1 E1 = Yn2 E2 + · · · Ynn En
The first row of this set may now be neglected, leaving (n − 1) equations in (n − 1)
unknowns, E2 · · · En . In matrix form, this becomes
 



Y22 · · · Y2n
E2
I2 − Y21 E1
  ..

..
..   .. 
(10)
= .

.
.  . 
In − Yn1 E1
Yn2 · · · Ynn
En
or
Î = Ŷ Ê
(11)
The new matrix Ŷ is obtained from the full admittance matrix Y merely by removing the
row and column corresponding to the fixed-voltage busbar. (In the present case this refers to
the first row and column, though this need not be the case in general.)
In summation notation, the new equations are
Ii − Yi1 E1 =
n
Yik Ek
for i = 2, · · · n
(12)
k=2
which is a set of (n − 1) equations in (n − 1) unknowns. The equations are then solved for the
unknown voltages by any of the available techniques. Note that the problem of singularity
when there are no ground ties disappears if one row and column are removed from the Y
matrix.
Eliminating the unknown current I1 and the equation in which it appears is the simplest
way of dealing with the singularity problem, and reduces the order of the equations by one.
I1 is evaluated after the solution using the first equation in (8).
3
Analytical Definition of the Load Flow Problem
The variables in the power flow problem are the complex nodal voltages and currents. These
are related to each other by the linear nodal network equations (5),
I=Y E
and by the busbar constraints:
7
(13)
P Q busbar
sp
sp
sp
sp Ei Ii∗ = Pisp + jQsp
i = PGi − PLi + j QGi − QLi
(14)
where subscripts G and L signify the specified generation and load respectively connected to
the busbar i.
P V busbar
sp
sp
− PLi
Re {Ei Ii∗ } = Pisp = PGi
|Ei | =
Visp
(15)
(16)
Slack busbar
The slack busbar voltage is normally designated as the system angle reference, and its angle
is normally zero. In this case, the complex voltage is known:
Ei = Visp
(17)
Equations (14) - (17), written for all appropriate busbars, define with (13) the power flow
problem. This is a nonlinear set with the special feature that (13) is linear, a feature that is
made use of in many solution methods. Almost all solution algorithms are designed to provide
a solution directly for the voltages, rather than the currents. Another special feature of the
problem is that one complex voltage (the slack) in (13) is known. This case was discussed in
Section 2.4.
4
Newton-Raphson Method
The Newton-Raphson power flow method involves the formal application of a well-known
general algorithm for the solution of a set of simultaneous nonlinear equations f (x) = 0,
where f is a vector of functions f1 · · · fn in the variables x1 · · · xn .
This technique follows from a Taylor series expansion of f (x) = 0, i.e.,
f (x + ∆x) = f (x) + J (x)∆x + higher order terms
(18)
∂f
∂fi
where J (x) = ∂x is the square Jacobian matrix of f (x), with Jik = ∂x
. In developing
k
the solution technique, the higher order terms are neglected and (18) is solved iteratively.
Defining ∆xp := xp+1 − xp , (18) can be rewritten for the (p + 1)th iteration as
f (xp + ∆xp ) = f (xp ) + J (xp )∆xp
(19)
At each step in the iteration process, the value of ∆xp which makes f (xp +∆xp ) = f (xp+1 ) = 0
is determined. Hence (19) becomes
i.e.
0 = f (xp ) + J (xp )∆xp
(20)
∆xp = −J (xp )−1 f (xp )
(21)
8
f (x)
Dx p
tangent to f(x)
xp
x p)1
solution
Figure 3: Graphical interpretation of a Newton-Raphson iteration
Hence at each iteration of the Newton-Raphson method, the nonlinear problem is approximated by a linear matrix equation.
This linearizing approximation can best be visualised using a single-variable problem
f (x) = 0. Figure 3 gives the graphical interpretation of one iteration of (21) for this single variable case. Equation (21) can be restated for the single variable case as ∆xp = −f (xp )/f (xp ).
The method converges very rapidly (quadratically) if the initial estimates are good and
f (x) is well-behaved.
To use the algorithm for power flow solutions, it is merely required to write the equations
defining the power flow problem as a set f (x) = 0. There are any number of different ways of
writing these equations, but the most popular method is to use (6) to substitute for Ii in (14)
or (15). The Newton-Raphson algorithm can only handle real equations and variables, so the
complex equations are split into their real and imaginary parts, and the voltage variables are
taken as V and θ. This gives
= Ei Ii∗
Pisp + jQsp
i
n
= Ei
Yik∗ Ek∗
k=1
= Vi
n
ejθi (Gik − jBik )Vk e−jθk
k=1
= Vi
n
(Gik − jBik )Vk ej(θi −θk )
k=1
= Vi
n
(Gik − jBik )Vk (cos θik + j sin θik )
k=1
where θik = θi − θk . Therefore,
Pisp + jQsp
i = Vi
n
Vk [(Gik cos θik + Bik sin θik ) + j(Gik sin θik − Bik cos θik )]
k=1
The resulting load flow equations are:
9
P Q busbar
∆Pi =
∆Qi =
Pisp
Qsp
i
n
− Vi
Vk (Gik cos θik + Bik sin θik ) = 0
(22)
Vk (Gik sin θik − Bik cos θik ) = 0
(23)
k=1
− Vi
n
k=1
where ∆Pi and ∆Qi are called the active and reactive power mismatches at busbar i.
P V busbar
Only (22) is used, since Qsp
i is not available.
Slack busbar
No equations.
Note that the voltage magnitudes appearing in (22) and (23) for P V and slack busbars
are not variables, but are fixed at their specified values. Similarly θ at the slack busbar is
fixed.
The complete set of equations is made up of two for each P Q busbar and one for each
P V busbar. The problem variables are V and θ for each P Q bus and θ for each P V bus.
The number of variables is therefore equal to the number of equations. Equation (20) then
becomes




..
p 
p 
p
p
∆P
. N  ∆θ
 H
 ··· 
(24)
0 =  ···  − 
 · · · · · · · · ·  ∆V p
p
.
∆Q
.. Lp
Vp
Jp
where ∆P p are the real power mismatches at all P Q and P V buses, ∆Qp are the reactive
power
mismatches at all P Q buses, ∆θp are the θ corrections for all P Q and P V buses, and
∆V p
V p provide the V corrections for all P Q buses.
The division of each ∆Vip by Vip does not numerically affect the algorithm, but simplifies
some of the Jacobian matrix terms. For busbars i and k (not row i and column k in the
matrix),
∂∆Pi
∂θk
∂∆Pi
= −Vk
∂Vk
∂∆Qi
= −
∂θk
∂∆Qi
= −Vk
∂Vk
Hik = −
Nik
Jik
Lik
As an example, for the 4-busbar system of Figure 4, (24) becomes,
10
X
slack
1
2
3
4
X
Figure 4: Sample System




0=



∆P1
∆P3
∆P4
···
∆Q1
∆Q4


H11
0
H14


  0 H33 H34
 
  H
 −  41 H43 H44
 
  ··· ··· ···
 
 J
0
J14
 11
J41
J43
J44
..
.
..
.
..
.
···
..
.
..
.
N11 N14
0
N41
···
L11
L41



∆θ1

N34   ∆θ3


N44 
  ∆θ4

···
··· 
  ∆V1 /V1
L14 
 ∆V4 /V4
L44








(25)
The Jacobian matrix is symmetrical in structure but not value. It is highly sparse for
large networks, since mutual elements Hik , Nik , Jik , Lik , are only non-zero where a physical
connection between busbars i and k exists. The expressions for the calculation of the elements
of H, N , J and L are obtained by partial differentiation of (22) and (23) with respect to θ
and V . The expressions are as follows:
i = k
Hik = Lik = Vi Vk (Gik sin θik − Bik cos θik )
k
Nik = −Jik = Vi Vk (Gik cos θik + Bik sin θik ) i =
Hii
Nii
Jii
Lii
=
=
=
=
−Bii Vi2 − Qi
Gii Vi2 + Pi
−Gii Vi2 + Pi
−Bii Vi2 + Qi

















(26)
where Pi and Qi are the calculated nett busbar active and reactive powers, given by the
summation terms in (22) and (23).
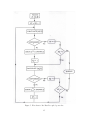
A logic flow-chart for the Newton Raphson method is shown in Figure 5.
It can be economical to calculate the mismatches and the Jacobian matrix elements in the
same subroutine, since many of the individual calculated terms can be used for both. This
can be seen by comparing (26) with (22) and (23).
11
24
Figure 5: Flow-chart of Newton-Raphson power flow
12
4.1
Practical Solution Considerations
The efficient solution of (24) at each iteration is crucial to the success of the Newton-Raphson
method. If conventional matrix techniques were to be used, the storage (an2 ) and computing
time (an3 ) would be prohibitive for large systems. In practice, the sparsity of the Jacobian
matrix is exploited, using sparsity-programmed ordered elimination. In this scheme, the way
in which the rows and columns of (24) are written is different to that shown, and only the
non-zero elements of the Jacobian matrix are stored and operated upon.
Alternative formulations of the Newton-Raphson power flow approach have been used.
One method is to express ∆Pi and ∆Qi in (22) and (23) in terms of the busbar voltages in
rectangular form ei + jfi , and to designate e and f as the problem variables (rectangular
power-mismatch version). The expressions for ∆Pi and ∆Qi are then partially differentiated
with respect to each ek and fk . Extra equations are needed for the P V busbar voltage
constraints. The Jacobian matrix is larger than, and different to, that in (24).
Other versions may be formulated by using current mismatches rather than power mismatches. The complex current mismatch equation at a P Q busbar i is obtained by substituting (14) into (6):
n
Pisp − jQsp
i
∆Ii =
−
Yik Ek = 0
(27)
Ei∗
k=1
The real and imaginary parts of ∆Ii are separated out, using either polar voltages (V and θ
as variables) or rectangular voltages (e and f as variables).
Convergence behaviour will differ for each different formulation.
4.2
Aids to Convergence
The Newton-Raphson method can diverge very rapidly or converge to the wrong solution if
the equations are not well-behaved or if the starting voltages are badly chosen. Such problems
can often be overcome by a variety of techniques. The simplest device is to impose a limit
on the size of each ∆θi and ∆Vi correction at each iteration. Figure 6 illustrates two cases
which would diverge without this device.
Another method is to obtain good starting values for θ and V , perhaps from a previous
solution. This also reduces the number of iterations required.
5
Fast Decoupled Power Flow
Numerical methods tend to be most successful when they take special advantage of the physical properties of the system being solved. This idea can be applied to the Newton-Raphson
(NR) power flow method (which is mathematically entirely general), to produce new algorithms with various computational advantages. The decoupled methods approximate the NR
power flow algorithm by using knowledge of the physical characteristics of electrical systems.
The decoupling principle recognises that in the steady state, active powers are strongly
related to voltage angles, and reactive powers to voltage magnitudes. However, there is quite
weak coupling between active powers and voltage magnitudes, and between reactive powers
and voltage angles. Referring back to the Jacobian matrix equation (24) of the NR method, it
is seen that the Jacobian sub-matrices J and N represent the weak P −V and Q−θ couplings.
13
Figure 6: Limited ∆x
Equations (26) indicate that because (for most practical power systems) Gik Bik and θik
is close to zero, the elements of J and N are small compared to those of H and L.
If we therefore neglect sub-matrices J and N we shall have approximated the Jacobian
matrix, and in particular will have decoupled the P − θ and Q − V problems. Equation (24)
can now be separated into two smaller matrix equations:
= H∆θ
(28)
∆Q = L[∆V /V ]
(29)
∆P
with the elements of H and L given by (26).
This not only reduces computation and storage for the construction and solution of these
equations, but it enables successive-displacement iteration to be performed between (28) and
(29). In this scheme (28) is first solved, and θ updated. Then the new θ are used in (29) to
solve for voltage magnitudes V . The initial rate of convergence of this block-successive type of
scheme is very fast in the power flow application. It takes only a small number of iterations to
reach normal convergence accuracies. However because the quadratic convergence property
has been sacrificed by the approximations, a high-accuracy solution may require many more
iterations.
(Note: The Jacobian matrix defines the directions in which the algorithm progresses. It
does not make the solution more approximate simply because the Jacobian matrix has been
approximated.)
The following assumptions are now made to simplify the elements of H and L:
cos θik 1 ; Gik sin θik Bik ; Qi Bii Vi2
These assumptions are physically justifiable for many practical power systems since the angle
between adjacent busbars in a power system is usually small and the resistance/reactance
ratio of most transmission lines is much less than unity. Also, Qi is normally very much
smaller than Bii . However the assumptions may not be so good for lower voltage distribution
systems where resistances are often large.
14
Equations (28) and (29) now become
∆P
= V t B V ∆θ
t
∆Q = V B V [∆V /V ]
(30)
(31)
The elements of B and B are now strictly elements of −B where B is the imaginary part
of the nodal admittance matrix Y defined in (4) as Y = G + jB.
The decoupling process and the final algorithmic form are now completed by:
• omitting from B the representation of those network elements that predominantly affect
reactive power flows, i.e. shunt reactances and off-nominal in-phase transformer taps.
• omitting from B the angle-shifting effects of phase shifting transformers.
• taking the left-hand V terms in (30) and (31) onto the left-hand sides of the equations,
and then in (30) removing the influence of reactive power flows on the calculation of ∆θ
by setting all the right-hand V terms to 1 p.u. Note that the V terms on the left-hand
side of (30) and (31) affect the behaviours of the defining functions and not the coupling.
Transferring V to the left-hand sides makes the equations more linear and hence easier
to solve.
• neglecting series resistances in calculating the elements B .
The final fast decoupled load flow equations become
[∆P /V ] = B ∆θ
[∆Q/V ] = B ∆V
(32)
(33)
where
= −1/Xik (i = k)
Bik
n
Bii =
1/Xik
k=1
k=i
B = −Bik
It is clear that elements of B must be derived and stored separately from those of B . The
latter are the negated imaginary elements of the admittance matrix.
Both B and B are real, sparse and have the structures of H and L respectively. Since
they contain only network admittances they are constant. Therefore they need be factorised
once only at the beginning of the study, whereas the NR method requires re-factorisation at
each iteration as the solution proceeds.
The steps in the power flow solution are:
(i) Form B and B and factorise them.
(ii) Choose the initial voltage estimates (magnitude and angle). Normally, the choice of
starting point is either a flat start (with all unspecified voltage magnitudes at unity and
all angles set to zero) or from the solution point of a previous study.
15
(iii) At each iteration cycle
- calculate the terms [∆P /V ] from
∆Pi /Vi =
Pisp /Vi
−
n
Vk (Gik cos θik + Bik sin θik )
(34)
Vk (Gik sin θik − Bik cos θik )
(35)
k=1
- solve (32) for ∆θ
- update the values of θ
- use the new θ to calculate [∆Q/V ] from
∆Qi /Vi =
Qsp
i /Vi
−
n
k=1
- solve (33) for ∆V
- update the values of V
(iv) Continue the iteration loop (iii) until the mismatches (represented by [∆P /V ] and
[∆Q/V ] are sufficiently small at all busbars.
The flow diagram of the process is given in Figure 7. The convergence testing logic permits
the calculation to terminate after a ∆θ solution (called a 1/2 iteration).
5.1
Comparison with the Newton Raphson Method
The main computational effort of the fast decoupled method (apart from initially factorizing
the B and B matrices) is the calculation at each iteration of the mismatch vectors [∆P /V ]
and [∆Q/V ]. This is much less computation than is required by the NR method where the full
Jacobian J is built and factorized each iteration. Typically a NR iteration takes around five
times as long as a fast decoupled iteration. However the fast decoupled method requires more
iterations than the NR method, taking in the order of two times as many iterations for normal
power systems with normal loading conditions. Consequently the fast decoupled method is
much faster for ‘normal’ systems and for moderate accuracy. Under these circumstances it is
also very reliable.
However, if the system is stressed (i.e. is operating close to its limits), or if it contains
R
ratios, then convergence of the fast decoupled
a significant proportion of lines with high X
method can become slow and unreliable. This occurs because the assumptions upon which
the fast decoupled method is based are no longer valid. Because the NR technique does not
rely on any such assumptions, it is more robust and will often converge reliably in situations
where the fast decoupled method would not converge.
If high accuracy is required for the solution, then the NR method is more suitable than
the fast decoupled method. The NR method recalculates the Jacobian J at each iteration,
so near the solution point, the ∆θ and ∆V updates always drive the process closer and
closer toward that solution point. On the other hand, the fast decoupled method uses an
approximate relationship between ∆P , ∆Q and ∆θ, ∆V . It therefore cannot be guaranteed
that at each iteration the updates ∆θ, ∆V will drive the process closer to the solution point.
The values of V , θ obtained at each iteration may bounce around the actual solution point.
Convergence is slowed, and in fact may not occur at all.
16
32
33
Figure 7: Flow-chart of the Fast Decoupled power flow
17
The fast decoupled method has an advantage over the NR method if storage requirements
are critical. Because the fast decoupled method does not store the J and N sub-matrices, its
storage requirements are typically only 70% of those of the NR method.
References
[1] I.A. Hiskens, “Network solution techniques for transmission planning”, ACADS Seminar
on Power System Analysis Software, Brisbane, November 1989.
[2] W.F. Tinney and J.W. Walker, “Direct solution of sparse network equations by optimally
ordered triangular factorization”, Proc. IEEE, Vol. 55, 1967, pp. 1801-1809.
[3] W.F. Tinney and C.E. Hart, “Power flow solution by Newton’s Method”, IEEE Trans.
on Power Apparatus and Systems, Vol. PAS-86, November 1967, pp. 1449-1456.
18