* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Document
Crystal radio wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Index of electronics articles wikipedia , lookup
Regenerative circuit wikipedia , lookup
Schmitt trigger wikipedia , lookup
Power electronics wikipedia , lookup
Operational amplifier wikipedia , lookup
Zobel network wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Two-port network wikipedia , lookup
Surge protector wikipedia , lookup
Electrical ballast wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Opto-isolator wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
Power MOSFET wikipedia , lookup
Current mirror wikipedia , lookup
Current source wikipedia , lookup
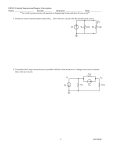
1. A 12.6 V battery is in a circuit with a 30 mH inductor and a 0.150 Ω resistor, as in Figure 1. The switch is closed at t=0. (a) Find the time constant of the circuit. (b) Find the current after one time constant has elapsed. (c) Calculate the energy in the inductor after one time constant has elapsed. (d) Find the voltage drops across the resistance when t= 0 and t= one time constant. (e) What’s the rate of change of the current after one time constant? Figure 1 2. A 6.0 V battery is connected in series with a resistor and an inductor. The series circuit has a time constant of 600 μs, and the maximum current is 300 mA. What’s the value of the inductance? 3. Calculate the resistance in an RL circuit in which L = 2.50 H and the current increases to 90.0% of its final value in 3.00 s. 4. How much energy is stored in a 70 mH inductor at an instant when the current is 2.00 A? 5. A 24 V battery is connected in series with a resistor and an inductor, with R= 8.0 Ω and L= 4.0 H, respectively. Find the energy stored in the inductor (a) when the current reaches its maximum value and (b) one time constant after the switch is closed. 6. An AC voltage source has an output of Δv= (2.00×102 V) sin 2πft. This source is connected to a 1.00×102 Ω resistor as in Figure 2. Find the rms voltage and rms current in the resistor. Figure 2 7. An 8.00 μF capacitor is connected to the terminals of a 60.0 Hz AC source whose rms voltage is 150 V. Find the capacitive reactance and the rms current in the circuit. 8. In a purely inductive AC circuit (see Fig. 3), L= 25.0 mH and the rms voltage is 150 V. Find the inductive reactance and rms current in the circuit if the frequency is 60.0 Hz. Figure 3 9. A series RLC AC circuit has resistance R= 250 Ω, inductance L=0.600 H, capacitance C= 3.50 μF, frequency f= 60.0 Hz, and maximum voltage Δvmax= 150 V. Find (a) the impedance, (b) the maximum current in the circuit, (c) the phase angle, and (d) the maximum voltage across the elements. 10. Calculate the average power delivered to the series RLC circuit in Ex 9. 11. Consider a series RLC circuit for which R = 150 Ω, L = 20.0 mH, ΔVrms = 20.0 V, and f= 796 s-1. (a) Determine the value of the capacitance for which the rms current is a maximum. (b) Find the maximum rms current in the circuit. Answers 1. (a)0.200 s (b) 53.1 A (c) 42.3 J (d) 0 V; 7.97 V (e) 150A/s 2. 12mH 3. 1.92 Ω 4. 0.140 J 5. (a) 18 J (b) 7.2 J 6. (a) 141 V (b) 1.41 A 7. (a) 332 Ω (b) 0.452 A 8. (a) 9.42 Ω (b) 15.9 A 9. (a) 588 Ω (b) 0.255 A (c) -64.8o (d) 63.8V; 57.6V; 193V 10. 8.12 W 11.(a) 2.00×10-6 F (b) 0.133 A