Download INTRODUCTION TO QUANTUM SUPERCONDUCTING CIRCUITS

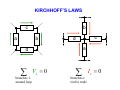
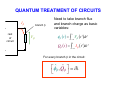
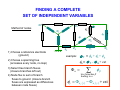
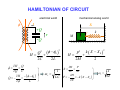
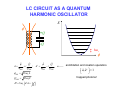
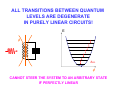
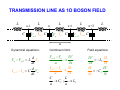
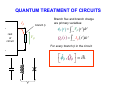
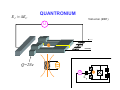
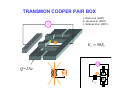
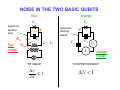
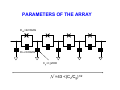
INTRODUCTION TO QUANTUM
SUPERCONDUCTING CIRCUITS:
PART 1
QUAN
ELEC
UM – MECHANICAL
RONICS LAB
Applied Physics and Physics, Yale University
R. VIJAY (U.C.Berkeley)
I. SIDDIQI (U.C.Berkeley)
C. RIGETTI
M. METCALFE (NIST)
V. MANUCHARIAN
N. BERGEAL (ESPCI Paris)
F. SCHACKERT
A. KAMAL
B. HUARD (ENS Paris)
A. MARBLESTONE (MIT)
N. MASLUK
M. BRINK
K. GEERLINGS
L. FRUNZIO
M. DEVORET
Acknowledgements: R. Schoelkopf, S. Girvin, D. Prober & D. Esteve
W.M.
KECK
Rutgers
Dec. 09
MESOSCOPIC ELECTRONS vs PHOTONS
INDEPENDENT ELECTRON INTERFERENCES
DIRECTLY REVEAL QUANTUM MECHANICS
Schrödinger's equation
Example: Sharvin-Sharvin & A.B. effects
Φ
2
⎡ 2⎛
⎤
eA ⎞
∂
∇
−
+
Ψ
=
Ψ
i
eU
i
⎢ ⎜
⎥
⎟
∂t
⎠
⎢⎣ m ⎝
⎥⎦
Interactions provide further quantum effects
INDEPENDENT PHOTON INTERFERENCES
DO NOT DIRECTLY REVEAL QUANTUM MECHANICS
Maxwell's equations
(
)
(
∂
c∇ × E + icB = i
E + icB
∂t
Planck's constant drops out!
Need ph-ph interactions....
)
QUANTUM OPTICS
QUANTUM RF CIRCUITS
FIBERS, BEAMS
TRANSM. LINES, WIRES
BEAM-SPLITTERS
COUPLERS
MIRRORS
CAPACITORS
LASERS
~
GENERATORS
PHOTODETECTORS
AMPLIFIERS
ATOMS
JOSEPHSON JUNCTIONS
ADVANTAGES OF CIRCUITS: - PARALLEL FABRICATION METHODS
- LEGO BLOCK CONSTRUCTION OF HAMILTONIAN
- ARBITRARILY LARGE ATOM-FIELD COUPLING
DRAWBACKS OF CIRCUITS:
ARTIFICIAL ATOMS PRONE TO VARIATIONS
SELECTED BIBLIOGRAPHY
ON QUANTUM CIRCUITS
Michel Devoret, in "Quantum Fluctuations", S. Reynaud, E. Giacobino,
J. Zinn-Justin, Eds. (Elsevier, Amsterdam, 1997) p. 351-385
Michel Devoret & John Martinis, Quant. Inf. Proc., 3, 351-380 (2004)
Robert J. Schoelkopf & Steve M. Girvin, Nature 451, 664-669 (2008)
John Clarke & Frank K. Wilhelm, Nature 453, 1031-1042 (2008)
OUTLINE
TODAY:
TOMORROW:
PRESENT BASIC CIRCUIT ELEMENTS
COMPARE QUBIT CIRCUITS
SUPERCONDUCTING CIRCUIT ELEMENTS
CAPACITANCE
INDUCTANCE
RESISTANCE
SUPERCONDUCTING CIRCUIT ELEMENTS
e2
EC =
2C
CAPACITANCE
EL =
2
2
4e L
EJ =
INDUCTANCE
RESISTANCE
2
4e 2 L J
TRANSMISSION LINES ARE JUST
L's AND C's
L
L
C
L
C
L
C
L
C
LIKEWISE, EVERY LINEAR PASSIVE RECIPROCAL RF COMPONENT IS BUILT
FROM INDUCTANCES AND CAPACITANCES
RESISTORS CAN BE THOUGHT OF AS INFINITE TRANSMISSION LINES
(NYQUIST, CALDEIRA & LEGGETT)
DYNAMICAL VARIABLES OF CIRCUIT
CIRCUIT : ARBITRARY NETWORK OF ELECTRICAL ELEMENTS
node n
element
Vnp
branch
np
loop
Inp
node p
TWO DYNAMICAL VARIABLES CHARACTERIZE THE STATE
OF EACH DIPOLE ELEMENT AT EVERY INSTANT:
Voltage across the element:
Vnp ( t ) = ∫ E ⋅ d
p
n
Current through the element:
I np ( t ) = ∫∫ j ⋅ dσ np
Signals:
any linear
combination
of these variables
CONSTITUTIVE RELATIONS
OF CIRCUIT ELEMENTS
linear inductance:
V = L dI/dt
non-linear inductance:
linear capacitance:
I = C dV/dt
E = LI2/2= Φ2/2L
E = f(Φ)
f non-quadratic
E = CV2/2= Q2/2L
Inductances and capacitances are "bottles" for electric and magnetic fields
KIRCHHOFF’S LAWS
b
c
a
b
b
d
∑ λ Vλ = 0
branches
around loop
c
d
a
b
∑ν
branches
tied to node
Iν = 0
CONSTITUTIVE RELATIONS
+
KIRCHHOFF'S LAWS
MAXWELL'S
EQUATIONS
ON A
NETWORK
QUANTUM TREATMENT OF CIRCUITS
Iβ
rest
of
circuit
branch β
Vβ
Need to take branch flux
and branch charge as basic
variables:
φβ ( t ) = ∫ Vβ ( t ')dt '
t
−∞
Qβ ( t ) = ∫ I β ( t ')dt '
t
−∞
For every branch β in the circuit:
⎡φˆβ , Qˆ β ⎤ = i
⎣
⎦
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Method of nodes
1) Choose a reference electrode
(ground)
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Method of nodes
1) Choose a reference electrode
(ground)
2) Choose a spanning tree
(accesses every node, no loop)
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Method of nodes
1) Choose a reference electrode
(ground)
2) Choose a spanning tree
(accesses every node, no loop)
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Method of nodes
1) Choose a reference electrode
(ground)
2) Choose a spanning tree
(accesses every node, no loop)
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Method of nodes
φb
φc
φa
1) Choose a reference electrode
(ground)
2) Choose a spanning tree
(accesses every node, no loop)
3) Select tree branch fluxes
(closure branches left out)
φd
φg
φf
φe
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Φ2
Method of nodes
Φ3
Φ7
Φ1
Φ6
1) Choose a reference electrode
(ground)
2) Choose a spanning tree
(accesses every node, no loop)
3) Select tree branch fluxes
(closure branches left out)
4) Node flux is sum of branch
fluxes to ground (closure branch
fluxes are expressed as differences
between node fluxes)
Φ4
Φ5
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Φ2
Method of nodes
Φ3
φh
Φ1
φf
1) Choose a reference electrode
(ground)
2) Choose a spanning tree
(accesses every node, no loop)
3) Select tree branch fluxes
(closure branches left out)
4) Node flux is sum of branch
fluxes to ground (closure branch
fluxes are expressed as differences
between node fluxes)
φd
Φ4
example:
Φ7
φg
Φ6
φe
Φ5
Φ 7 = φd + φe + φg
φh = Φ 7 - Φ 6 + cst
FINDING A COMPLETE
SET OF INDEPENDENT VARIABLES
Φ2
Method of nodes
Φ3
φh
Φ1
φf
1) Choose a reference electrode
(ground)
2) Choose a spanning tree
(accesses every node, no loop)
3) Select tree branch fluxes
(closure branches left out)
4) Node flux is sum of branch
fluxes to ground (closure branch
fluxes are expressed as differences
between node fluxes)
φd
φg
Φ6
φe
Φ4
example:
Φ7
Φ5
Φ 7 = φd + φe + φg
φh = Φ 7 - Φ 6 + cst
Φn =
∑
tree branches β
leading to n
φβ
φγ = Φ n (γ ) − Φ n (γ ) + cst
+
−
TWO METHODS FOR DEFINING A COMPLETE
SET OF INDEPENDENT VARIABLES
Method of nodes
Method of loops
Defines loop charges
HAMILTONIAN OF CIRCUIT
mechanical analog world
electrical world
φ
I
X
+Q
-Q
V
M
Q (φ − φ0 )
H=
+
2C
2L
2
φ=
∂H Q
=
∂Q C
∂H − (φ − φ0 )
Q=−
=
L
∂φ
ωr =
f
2
1
LC
k
k ( X − X0 )
P
H=
+
2M
2
2
∂H
P
=
X=
∂P M
∂H
P=−
= −k ( X − X 0 )
∂X
2
ωr =
k
M
A SUPERCONDUCTING CIRCUIT
BEHAVING LIKE AN ATOM?
SIMPLEST EXAMPLE: SUPERCONDUCTING
MICROFABRICATION
LC OSCILLATOR
CIRCUIT
L ~ 3nH, C ~ 10pF, ωr /2π ~ 2GHz
ELECTRONIC FLUID SLOSHES BACK AND FORTH
FROM ONE PLATE TO THE OTHER, INTERNAL MODES FROZEN
BEHAVES AS A SINGLE CHARGE CARRIER
DEGREE OF FREEDOM IN ATOM vs CIRCUIT
Superconducting
LC oscillator
Example of Rydberg atom
L
velocity of electron →
force on electron →
voltage across capacitor
current through inductor
C
LC CIRCUIT AS A QUANTUM
HARMONIC OSCILLATOR
E
φ
+Q
-Q
hω r
φ
φˆ
Qˆ
φˆ
Qˆ
†
aˆ =
; aˆ =
+i
−i
φZPF QZPF
φZPF QZPF
φZPF = 2 ωr L
(
⎡⎣ aˆ , aˆ † ⎤⎦ = 1
trapped photons!
QZPF = 2 ωr C
Hˆ = ωr aˆ † aˆ + 1
annihilation and creation operators
2
)
ALL TRANSITIONS BETWEEN QUANTUM
LEVELS ARE DEGENERATE
IN PURELY LINEAR CIRCUITS!
E
φ
hω r
φ
CANNOT STEER THE SYSTEM TO AN ARBITRARY STATE
IF PERFECTLY LINEAR
NEED NON-LINEARITY TO FULLY
REVEAL QUANTUM MECHANICS
Potential energy
Position coordinate
JOSEPHSON TUNNEL JUNCTION
PROVIDES A NON-LINEAR INDUCTOR
WITH NO DISSIPATION
S
1nm
I
S
Ι
Ι
LJ
superconductorinsulatorsuperconductor
tunnel junction
Ι = φ / LJ
CJ
LJ =
φ0
I0
I0
φ
φ = ∫−∞ V ( t ')dt '
t
I = I 0 sin (φ / φ0 )
φ0 =
2e
JOSEPHSON TUNNEL JUNCTION
PROVIDES A NON-LINEAR INDUCTOR
WITH NO DISSIPATION
S
1nm
I
S
superconductorinsulatorsuperconductor
tunnel junction
LJ
CJ
LJ =
U = − EJ cos (φ / φ0 )
Ι
φ = ∫−∞ V ( t ')dt '
t
φ02
EJ
φ
2 EJ
bare Josephson potential
φ0 =
2e
TRANSMISSION LINE AS 1D BOSON FIELD
L
n-1
C
L
Vn −1 I n −1 C
n
L
L
n+1
Vn I n C
n+2
L
Vn +1 I n +1 C
a
Dynamical equations:
d
Vn − Vn +1 = L I n
dt
d
I n −1 − I n = C Vn
dt
Continuum limit:
Field equations:
Vn +1 − Vn
∂V
→
∂x
a
I n +1 − I n
∂I
→
∂x
a
C
L
→C ; → L
a
a
∂V
= −L
∂x
∂I
= −C
∂x
∂I
∂t
∂V
∂t
CHARGE AND FLUX IN CONTINUUM LIMIT
Φ ( x)
Lδx
Π ( x)δ x
Φ ( x + δ x)
Lδx
C δx
Lδx
C δx
Π ( x + δ x)δ x
δx
⎡⎣Φ ( x ) , Π ( x ) δ x ⎤⎦ = i
⎡⎣Φ ( x ) , Π ( x + δ x ) δ x ⎤⎦ = 0
δx→0
ˆ ( x ),Π
ˆ ( x )⎤ = i δ ( x − x )
⎡Φ
1
2 ⎦
1
2
⎣
Hamiltonian : energy density as a function of field and conjugate momentum:
2
2⎫
+∞
⎧ 1 ˆ
1
ˆ
ˆ
⎡
⎤
⎡
⎤
H = ∫ dx ⎨
Π ( x )⎦ +
∇Φ ( x ) ⎦ ⎬
⎣
⎣
−∞
2L
⎩ 2C
⎭
COMPATIBILITY WITH STANDARD QED
For simplest geometry, consider stripline waveguide:
w
y
h
x
z
B ( x1 , y1 , z1 )
E ( x2 , y2 , z2 )
Flux between strips:
x
yb + h
−∞
yb
ˆ ( x ) = 1 dx
Φ
1
∫ ∫
Strip charge per unit length:
dy Bˆ z ( x, y, z1 )
ˆ (x ) = ε
Π
2
0∫
z f +w
zf
dz Eˆ y ( x2 , y2 , z )
Commutation relations between field operators in standard QED:
i ∂
⎡ Bˆ z ( x1 , y1 , z1 ) , Eˆ y ( x2 , y2 , z2 ) ⎤ =
⎣
⎦ ε ∂x δ ( x1 − x2 ) δ ( y1 − y2 ) δ ( z1 − z2 )
0
1
ˆ ( x ),Π
ˆ ( x )⎤ = i δ ( x − x )
⎡Φ
1
2 ⎦
1
2
⎣
OK!
END OF 1ST LECTURE
INTRODUCTION TO QUANTUM
SUPERCONDUCTING CIRCUITS:
PART 2
QUAN
ELEC
UM – MECHANICAL
RONICS LAB
Applied Physics and Physics, Yale University
R. VIJAY (U.C.Berkeley)
I. SIDDIQI (U.C.Berkeley)
C. RIGETTI
M. METCALFE (NIST)
V. MANUCHARIAN
N. BERGEAL (ESPCI Paris)
F. SCHACKERT
A. KAMAL
B. HUARD (ENS Paris)
A. MARBLESTONE (MIT)
N. MASLUK
M. BRINK
K. GEERLINGS
L. FRUNZIO
M. DEVORET
Acknowledgements: R. Schoelkopf, S. Girvin, D. Prober & D. Esteve
W.M.
KECK
Rutgers
Dec. 09
OUTLINE
YESTERDAY:
TODAY:
PRESENT BASIC CIRCUIT ELEMENTS
COMPARE QUBIT CIRCUITS
QUANTUM TREATMENT OF CIRCUITS
Iβ
rest
of
circuit
branch β
Branch flux and branch charge
are primary variables:
φβ ( t ) = ∫ Vβ ( t ')dt '
t
−∞
Vβ
Qβ ( t ) = ∫ I β ( t ')dt '
t
−∞
For every branch β in the circuit:
⎡φˆβ , Qˆ β ⎤ = i
⎣
⎦
IRREVERSIBLE/REVERSIBLE
CHARGE TRANSFER
e tunneling
quasiparticle
energy
2Δ
rate
before
SIS
TUNNEL
JUNCTION
after
IRREVERSIBLE/REVERSIBLE
CHARGE TRANSFER
e tunneling
quasiparticle
energy
2Δ
rate
before
SIS
TUNNEL
JUNCTION
after
2e CP tunneling
quasiparticle
energy
matrix
element
DYNAMICS OF JOSEPHSON ELEMENT
FROM CHARGE POINT OF VIEW
(IN ABSENCE OF Q.P. TUNNELING)
integer
Hopping
N0 − 1 N0 N0 + 1
Q
=N
2e
1
h / e2
M = EJ =
Gt Δ
2
16
Charge states:
N̂ N = N N
Josephson tunneling hamiltonian in charge basis:
EJ
ˆ
HJ = −
2
∑( N
N
N +1 + N +1 N
)
FROM NUMBER TO "PHASE" REPRESENTATION
ϕˆ = 2eφˆ /
⎡ϕˆ , Nˆ ⎤ = i
⎣
⎦
eiϕˆ Nˆ e − iϕˆ = Nˆ − 1
EJ
ˆ
HJ = −
N N +1 + N +1 N
(
∑
2 N
EJ iϕˆ
(from expression of
− iϕˆ
= − ( e + e ) translation operator)
2
= − EJ cos ϕˆ
(
= − EJ cos φˆ / φ0
Josephson's
ϕ
)
)
ϕ
Φ0
φ0 = =
2e 2π
runs on a line but tunnel hamiltonian is periodic
ELECTRODYNAMICS OF JUNCTION IN ITS ENVRONMENT
REST
OF
CIRCUIT
Z (ω )
CJ
EJ
U(t)
2
φ ( t ) = ∫−∞ ∫ E ( x,τ ) dxdτ
t
1
N.B. The electric field E
encompasses here all
contributions of the force
on the electrons doing work,
including those usually
called chemical potential
effects.
ELECTRODYNAMICS OF JUNCTION IN ITS ENVRONMENT
t
Qext = ∫ Idτ
−∞
Q = 2eN
REST
OF
CIRCUIT
EJ
QC
Z (ω )
CJ
U(t)
2
φ ( t ) = ∫−∞ ∫ E ( x,τ ) dxdτ
t
1
Equation of motion:
∂
CJ φ +
∂φ
⎡
⎛ φ ⎞⎤
⎢ − EJ cos ⎜ ⎟ ⎥ = I φ , φ ,....
⎝ φ0 ⎠ ⎦
⎣
(
)
Can be obtained in general from a Lagrangian:
d ∂L ∂L
−
=0
dt ∂φ ∂φ
CJ 2
φ
L = L J +L ext =
φ + EJ cos + L ext φ , φ ,...
2
φ0
(
)
TWO CHARACTERISTIC ENERGIES OF
ENVIRONMENT
Total environment admittance:
Effective shunt capacitance of junction:
Effective shunt inductance of junction
Ytot (ω ) = iCJ ω + Z −1 (ω )
Im ⎡⎣Ytot (ω ) ⎤⎦
CΣ = lim
ω
ω →0
Leff
⎧⎪ ⎡
⎤ ⎫⎪
1
= lim ⎨Im ⎢
⎥⎬
ω →0
⎩⎪ ⎣ ωYtot (ω ) ⎦ ⎭⎪
(electron charge
appears here instead
of Cooper pair charge
for convenience in
some formulas)
2
Coulomb charging energy
Inductive energy
e
EC =
2CΣ
EL
h / 2e )
(
=
Leff
2
(form chosen for
easy comparison
with Josephson
energy)
TWO BASIC SUPERCONDUCTING "ATOMS"
flux
charge
superconducting
island
LJ
superconducting
loop
ϕ∈
LJ
N∈
CJ
Φext
L > LJ
Cg
CJ
U
I
"HYSTERETIC RF SQUID"
E J > EL
EC
Δϕ
2π
Friedman et al. (2000)
"COOPER PAIR BOX"
1
EL = 0; EJ
EC
ΔN < 1
Bouchiat et al. (1998), Nakamura, Pashkin, Tsai (1999)
PHASE POTENTIALS OF SQUID AND BOX
E J > EL
EL = 0; EJ
EC
EC
E
SQUID
BOX
max. curvature
= EL − E J
2EJ
−1
2eΦ ext /
0
ϕ
2π
+1
+2
−
ϕ
2π
1
2
e
+
1
2
iπ C gU / e
RICH LEVEL STRUCTURE, BUT EXTREME SENSITIVITY TO NOISE
09-III-10
PHASE-CHARGE DUALITY
E J > EL
EL = 0; EJ
EC
EC
E
SQUID
BOX
8 EC N g −
2π EL ϕext − π
−1
0
ϕ
2π
+1
+2
1
2
−1
+1
0
N
+2
CHARGE QUBIT FAMILY
THE SINGLE COOPER PAIR BOX
ARTIFICIAL ATOM
EJ
Bouchiat et al. (1998)
Nakamura, Tsai and Pashkin (1999)
0.5EC
U
Φ
U
Q=2Ne
Φ
Cg
EJ
4 EC
QUANTRONIUM
Vion et al. (2001)
U
Φ
Q=2Ne
Φ
U
Cg
TRANSMON COOPER PAIR BOX
J. Koch et al. (2007)
A. Houck et al. (2007)
J. Schreier et al. (2007)
U
Φ
EJ
50 EC
U
Q=2Ne
Φ
Cg
Cottet et al. (2002)
Koch et al. (2007)
ANHARMONICITY vs OFFSET CHARGE
INSENSITIVITY IN COOPER PAIR BOX
gap
EJ
"C.P. BOX"
"QUANTRONIUM"
"TRANSMON"
FLUX QUBIT FAMILY
EXAMPLES OF QUANTUM CIRCUITS
BELONGING TO THE RF-SQUID TYPE
Readout
Readout
Friedman, Patel, Chen, Tolpygo and J. E. Lukens,
Nature 406, 43 (2000).
Chiorescu, Nakamura, Harmans & Mooij,
Science 299, 1869 (2003).
"flux" qubit
"phase" qubit
Readout
Steffen et al., Phys. Rev. Lett. 97, 050502 (2006)
FLUXONS PLAY WITH FLUX QUBITS
A ROLE SIMILAR TO WHAT
COOPER PAIRS PLAY WITH CHARGE QUBITS
Inductive energy
-1
0
1
Φ
Φ0
⎛
EJ ⎞
~ exp ⎜⎜ −α
⎟⎟
E
C ⎠
⎝
OUR RECENT CHILD IN
FLUX QUBIT FAMILY
NOISE IN THE TWO BASIC QUBITS
superconducting
loop
flux
charge
LJ
LJ
ϕ
ΦN
Φext
flux
superconducting
island
CJ
L ∼ LJ
noise!
N
Cg
CJ
UN
U
charge
noise!
I
"RF SQUID"
Δϕ
2π
1
"COOPER PAIR BOX"
ΔN < 1
FLUXONIUM IDEA: SHUNT A COOPER PAIR BOX
AT DC, LEAVE IT UNSHUNTED AT RF
L
LJ
LJ
Cg
CJ
UN
U
Manucharyan. et al., Science, 326, 113; arxiv 0906.0831
Koch. et al., Phys. Rev. Lett, to appear; arxiv 0902.2980
Manucharyan. et al., submitted to Nature, arxiv 0910.3039
PRACTICAL IMPLEMENTATION
write
/
d
a
e
r
Small junction:
EJ/EC = 3.6
Array junctions (N =43):
EJA/ECA = 28
Readout
f0 = 8 GHz;
Q=400
Every island is shunted by at least one large junction: array performs as inductor
CHIP AND MODEL
“Atom”
EC = ½ e2/(CJ+Cc)=2.5 GHz
EJ = ½ (Φ0/2π)2/LJ=8.9GHz
EL = ½ (Φ0/2π)2/L=0.52GHz
“Cavity”
ωR=(LRCR)-1/2/2π = 8.2GHz
ZR=(LR/CR)1/2 = 82Ω
Coupling constant
g = ωR(ZR/2RQ)1/2 /(1+CJ/Cc)
= 135MHz (RQ=1 kΩ)
CJ/Cc=11
PARAMETERS OF THE ARRAY
EJA=22.5GHz
ECA=0.8GHz
Cg~CJ/2000
N =43 <(CJ/Cg)1/2
TWO-TONE SPECTROSCOPY vs EXTERNAL FLUX
Φ0
Φ≈
2
0-3 transition
Parasitic resonance in the array
(accounted by a minor model correction)
0-2 transition
Inset:
0-2 transition symmetry-forbidden
at zero flux
resonator & vacuum Rabi
0-1 transition
More than 106 points,
taken over >72 hours
w/o jumps or drifts!
NO OFFSET CHARGE
THY vs EXP CONFIRMS SINGLE COOPER PAIR REGIME
V.Manucharyan, J.Koch, L.Glazman, M.Devoret,
Science, 326, 113; arxiv 0906.0831
LOCATING FLUXONIUM ON THE
SUPERCONDUCTING QUBIT MAP
A QUBIT OPERATING FOR ALL
VALUES OF FLUX
~350MHz
Inductive energy
9GHz
Potential energy
-1
1
0
Φext =1/4 Φ0
Φext =1/2 Φ0
Φ
Φ0
Φext = 0
~2EJ
2π
2π2EL
2π
4π
ϕ
Φ0
TWO-TONE SPECTROSCOPY vs EXTERNAL FLUX Φ ≈ 2
A 370MHz ATOM MEASURED THROUGH A 8.2GHz CAVITY?
atom transition 0-1: store/manipulate
atom transition 1-2: couple to readout
g12 = g <1|N|2> ~ 100MHz
ω12 - ωR ~ 1GHz
χ= g122/(ω12 - ωR) ~10MHz
At the same time ω01 << ωR
reflected phase (deg)
TIME DOMAIN COHERENCE
time (μs)
Time, ns
Frequency, GHz
COHERENCE AS A FUNCTION OF FLUX BIAS
∂Φ
T21/ f =
Q1=130,000
quasiparticles, quantum phase slips?
External flux Φ ext / Φ 0
∂ω01
A ⎡⎣ = 10−6 Φ 0 ⎤⎦
Time, ns
Frequency, GHz
COHERENCE AS A FUNCTION OF FLUX BIAS
External flux Φ ext / Φ 0
CONCLUSIONS AND PERSPECTIVES
QUANTUM CIRCUITS OFFER A RICH PLAYGROUND
FOR EMULATING EXISTING MANY-BODY QUANTUM
SYSTEMS AND CREATING NEW ONES
STRONG COUPLING, NON-PERTURBATIVE REGIME
IS EASILY ACCESSIBLE
PRESENT CHALLENGE IS QUBIT WITH BUILT-IN
ERROR-CORRECTION, AND MORE GENERALLY
QUANTUM FEEDBACK
MECHANICAL ANALOG OF RF SQUID
angle of pendulum : gauge invariant phase difference
moment of inertia of pendulum : junction capacitance
spring : loop inductance
torque due gravity : Josephson current
potential energy of pendulum : Josephson energy
U(ϕ )
ϕ
ϕ
MECHANICAL ANALOG OF COOPER PAIR BOX
angular velocity:
Cg U
Ω=
CΣ φ0
rotating
magnet
ϕ̂
compass needle
needle
angular momentum:
Nh
torque on needle due to magnet
current through junction
velocity of needle in magnet frame
voltage across junction
Introduction to quantum superconducting circuits
1) Usual 2deg physics: circuit with normal electrons.
quantum circuits means that the electron obeys S. equation over the whole scal
of circuit. Electron propagate as Fermi waves
2) What about electromagnetic Bose wave propagation?
⎡−
⎤
∂
Δ + U ( x, t ) ⎥ Ψ ( x, t ) = i
Ψ ( x, t )
⎢
∂t
⎣ m
⎦
2
(
)
c∇ × E + icB = i
(
∂
E + icB
∂t
)
3) Need non-linearity. But usually, non-linear element are also
dissipative. Dissipation not good for QM
4) Josephson element: non-linear, non-dissipative, point-like
5) Lumped element electromagnetism: L and C's
6) L bottle for B field. C bottle for E field.
Constitutive equations
+ Kirchhoff equations for circuits are equivalent to Maxwell's equation
Define flux and charge for one element
Flux and charge are conjugate variables
How do we understand it?
2 choices flux is position, charge is position
Connections between elements
Example of harmonic oscillator
Always in the correspondence limit
The Josephson junction non linear inductance
Two superconducting electrodes: islands
1sole degree of freedom in an island : its number of Cooper pair
Charge hopping between two islands (zero external field)
Gives back Josephson formula
Arrays of Josephson junctions tends toward inductances
Quantum phase slips
Conclusions: finite networks are caricature of distributed systems
infinite networks are more powerful than distributed systems
single junction is non-linear inductance. Infinite junction array
is linear inductance
Artificial Josephson junction atoms
3 types of energies
Capacitive environem: easy
Inductive environment: more sutble