Download Lecture Notes # 3

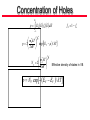
Lecture Notes # 3
• Understanding Density of States
– Solve 1-D Schrödinger equation for particlein-a-box
– Extend to 3-D
– Invoke periodicity requirement
– Solve for density of states
Review of Quantum Mechanics
H  
H  Hamiltonia n operator
  Mathematic wavefunct ion depicting
nature of electron in space/time
  Energy or allowable quantized energies
of that electron
• Often times you do not know  or , but
you have boundary conditions and want to
solve for possible values of  and a
functional form of 
Review of Quantum Mechanics
• Most general case: Time independent
 2 2
H
  U  x, y , z 
2m
Kinetic E.
Potential E.
• How do we know first part is K.E?
1 2
mv classicall y
2
1 2 p2
mv 
2
2m
pˆ  i is quantum momentum operator
KE 
1 2  2 2
So, mv 

2
2m
Review of Quantum Mechanics
For  r   exp ik  r 
pˆ   a
Momentum operator
Eigenvalue

pˆ   i r   i  r   iik  r   k r 
r
a = Momentum Eigenvalue
p  mv  k
k
v
 velocity of particle
m
Particle in a 1-D Box
• Free electron floating around in vacuum
• Let’s impose some boundary – confine it to a
region of space, a box or a unit cell in 1-D
U 
Confine it by setting U  
outside the box and U = 0
inside the box
U 
Confined
e-
U=0
0
L
x
• Since U(x) = 0 for 0<x<L, we can drop U(x) out
of the Hamiltonian, which becomes
 2 2
H

2m
Particle in a 1-D Box
• Because U   outside the box, we know the eCANNOT be there, so we get the boundary
condition:
 x  0   x  L   0
Because the Hamiltonia n must give
back an eigenvalue , we must pick
  f x  where f x   Af x 
and f 0  f L   0
• We do not care what happens between 0 and L,
so the simplest solution is just:
 n 
  A sin 
x , n  1,2,3,4...
 L 
for x  0, sin( 0)  0 OK
for x  L, sin( nL)  0 OK
Particle in a 1-D Box
• Plug  into the Schrödinger equation to make
sure H = E
 2 d 2 
 n

A
sin

2 
2m dx 
 L

x   

  2 d  n
 n
A cos

2m dx  L
 L
 2
2m

x  

 n 2 2
 n 
x  
 2 A sin 
 L 
 L
1  n 
 n
A
sin



2m  L 
 L
2
Energy, E


x

Particle in a 1-D Box
• Energy values are quantized since n
is an integer
• n=1 is lowest energy state, n=2 has
higher energy, etc.
n=4
E
n=3
9x
n=2
4x
n=1
18
0
16
14
L
• We can map out (x,n) vs. E
12
10
n  
E x 
2
 2mL
2
2
2



8
• Allowed energy states
6
4
2
0
0
1
2
n
3
4
Particle in a 1-D Box
• Now let’s fill up the states with electrons.
Suppose we have N e- we want to pour into our
1-D box.
• For N e- you can calculate the energies since
we know we can have 2e-/n states (two spins).
• So N electrons fills nF= N/2 states.
• The highest energy state, nF, gives F, the Fermi
energy.
2
F 
  nF  


2m  L 
Fermi-Dirac Distribution
• Fermi energy is well defined at
T = 0 K because there is no
n   

E x 
thermal promotion
 2mL 
• At high T, there is
F
thermalization, so F is not as
clear
2
2
18
16
14
2
12
2
10
8
6
4
2
0
0
1
2
n
3
• Officially defined as the energy where the probability of finding an
electron is ½
• This definition comes from the Fermi-Dirac Distribution:
1
f   
exp     / k BT   1
• This is the probability that an orbital (at a given energy) will be
filled with an e- at a given temperature
• At T=0, =F and  = F, so f(F)=1/2
4
Particle in a 3-D Box
• Let’s confine e- now to a 3-D box
• Similar to a unit cell, but e- is confined
inside by U   outside the box
• Schrödinger’s equation is now
 2  2
2
2 
 2  2  2  x, y, z    x, y, z 
2m  x y z 
• You can show that the answer is:
 nx   n y
 n x, y, z   A sin 
x  sin 
 L   L
  nz 
y  sin 
z
  L 
• We now have 3 quantum numbers nx, ny, and nz that are
totally independent
• (1,2,1) is energetically degenerate with (2,1,1) and (1,1,2)
Particle in a 3-D Box
• Now let’s repeat this box infinitely in each direction to get a
repeated “unit cell”
• What’s different about this situation?
– U(x,y,z)=0
– No region where U = infinity
• So, there’s really no reason that  x  0   x  L   0
since U  x  0  U  x  L   
• We don’t need those boundary conditions anymore
Periodic Boundary Condition
• For now, we don’t need such a strict boundary condition
• Make sure  is periodic with L, which would make each 3D box identical
• Because of this, we’ll have a periodic boundary condition
such that
 x  L, y, z    x, y, z 
• Wave functions that satisfy this periodic B.C. and are
solutions to the Schrödinger equation are TRAVELING
WAVES (not a standing wave anymore)
Periodic Boundary Condition
• Bloch function

 

 k r   exp ik  r

• Wave vector k satisfies

2
4
k x  0;
;
;...
L
L
• Etc. for ky and kz
• Quantum numbers are components of k of the form 2n/L
where n=+ or - integer
exp ik x x  L   exp i 2nx  L  / L
 exp i 2nx / Lexp i 2n
 exp i 2nx / L
 exp ik x x 
• Periodicity satisfied
Back to Schrödinger Equation
• Substitute

 

 k r   exp ik  r

into
 2  2
2
2  

 2  2  2  k r    k k r 
2m  x y
z 
gives

2 2 2 2
k 
k 
k x  k y2  k z2
2m
2m

• Important that kx can equal ky can equal kz or NOT
p̂  i
• The linear momentum operator



for  k r   exp ik  r



pˆ  k r   i k r   k k r 

so the plane wave  k r  is an eigenfunct ion
of linear momentum with an eigenvalue of
k , and the particle velocity in orbital k is
k
v
m


Fermi Level in 3-D
kx
• Similarly, can calculate a Fermi level
F 
Fermi level
2
 2
kF
2m
kF
kz
Vector in 3-D space
• Inside sphere k<kF, so orbitals are filled.
k
k>kF, orbitals are empty
• Quantization of k in each direction leads
to discrete states within the sphere
• Satisfy the periodic boundary conditions
at ± 2/L along one direction
This is a sphere only if
• There is 1 allowed wave vector k, with NOTE:
k =k =k . Otherwise, we have
an ellipsoid and have to
distinct kx, ky, kz quantum #s for the
recalculate everything. That can
3
volume element (2/L) in k-space
be a mess.
Sphere: GaAs (CB&VB), Si (VB)
• So, sphere has a k-space volume of
Ellipsoid: Si (CB)
y
x
4
V  k F3
3
y
z
Number of Quantum States
• Number of quantum states is
4 k 3
F
total volume
 3 3
volume of 1 allowed quantized state
2
L
• Since there are 2 e- per quantum state
 4 k 3 
 3 F  L3 3
N  2
 2 kF
3 
 2
 3
L 

V
N  2 k F3
3
Solve for k F ,
 
 3 N 

k F  
 V 
2
1
3
• Depends on e- concentration
 
Density of States
• Plug kF into
2 2
F 
k
2m
  3 N 


F 
2m  V 
2
2
2
3
• Relates Fermi energy to electron concentration
• Total number of electrons, N:
3
V  2m  2
N 2 2 
3   
• Density of states is the number of3 orbitals per unit energy
dN
V  2m  2 1 2
D  
 2 2  
d 2   
Relate to the surface of the sphere. For the next incremental growth in the sphere,
how many states are in that additional space?
Density of States
• Divide by V to get N/V which is electron density (#/cm3)
• Volume density of orbitals/unit energy for free electron gas
in periodic potential
3
1  2m  2 1 2
D   2  2  
2   
Starting point energy
Effective mass of e-
1  2m
D   2  2
2  
*
e



3
2
E  ECB  2
1
CB
Effective mass of h+
1  2m
 2
D  
2 
2  
*
h



3
2
EVB  E  2
1
Start from VB and go down
VB
Concentration of Electrons

n
 D E  f E dE  fun
e
e
EC
“EF”
3
 m kT  2
 exp   EC  / kT 
n  2
2 
 2 
*
e
 m kT 

N C  2
2 
 2 
*
e
3
2
Effective density of states in CB
n  NC exp  EC  EF  / kT 
Writing it with a minus sign indicates that as E difference between EC
and EF gets bigger, probability gets lower
Concentration of Holes
p
EV
 D E  f E dE
h
h
fh  1  fe

3
 m kT  2
 exp EV    / kT 
p  2
2 
 2 
*
h
 m kT 

NV  2
2 
 2 
*
h
3
2
Effective density of states in VB
p  NV exp EF  EV  / kT 
Intrinsic Carrier Concentration
  EC  EF   EF  EV  
n  p  N C NV exp 

kT


  EC  EV  
n  p  N C NV exp 

kT


EC  EV  EG , the band gap
n  p  NC NV exp EG / kT 
Entropy term
Enthalpy term
n  p  ni2
ni  intrinsic carrier concentrat ion
Constant for a given temperature.
Intrinsic = undoped
Intrinsic Carrier Concentration
  EG 
ni  N C NV exp 

2
kT


ni  constant for a given T means that
n  p is constant, too, which holds under
equilibriu m and away from it
•
•
•
•
ni
Ge: 2.4 x 1013 cm-3
Si: 1.05 x 1010 cm-3
GaAs: 2 X 106 cm-3
At 300 K
At temperature T, n = p by conservation
Add a field and np = constant, but n does not equal p
As n increases, p decreases, and vice versa
Useful to define Ei, which is Ei = EF when it is an intrinsic
semiconductor (undoped), so n = p = ni
  EC  Ei  
  Ei  EV  
ni  N C exp 
  NV exp 

kT
kT




Intrinsic Fermi Level
  EC  Ei  
  Ei  EV  
ni  N C exp 
  NV exp 

kT
kT




 NV 
  EC  Ei     Ei  EV  



  ln 
kT
kT

 

 NC 
 NV 

Ei  EC  EV  Ei  kT ln 
 NC 
 NV 

2 Ei  EV  EC  kT ln 
 NC 
 NV
2Ei  EV   EC  EV  kT ln 
 NC
EG kT  NV
Ei  EV    ln 
2
2  NC






Intrinsic Fermi Level
EG kT  NV
Ei  EV    ln 
2
2  NC



• This says that the intrinsic Fermi level (relative to the
valence band) is about mid-gap ± the (kT/2)ln(NV/NC)
scaling factor
kT  NV
ln 
2  NC
EG (eV)

  -13 meV for Si
1.12

35 meV for GaAS 1.42
0.67
- 7 meV for Ge
• So Ei for Si and Ge is slightly below mid-gap. Ei for GaAs is
slightly above. It is minor compared to EG, but just so you
know
• All of this has been intrinsic with no dopants
Dopants
• Let’s consider adding dopants
n-type
carriers n  ni  N D
ED
ECB
Ei
EVB
Depends
on EG, T
Depends on D, T, and
dopant density
 D  ECB  ED
At T=0, all donor states are filled. Hence, n = 0.
But at room temperature in P doped Si, 99.96%
of donor states are ionized.
At mid temperature, if N D  ni , then n  N D
At high temperature, such that
ni  N D , then n  ni
Dopants
n  p  ni2 still holds, just substitute
n  ni  N D
ni2
p
at room temperatu re, n  N D for typica l dopant densities
ni  N D
Say N D  1016 cm 3 
 N D  1016 cm 3 
 n  1016 cm 3
n  NC exp  EC  EF  / kT 
n 1016 cm 3
 19 3  exp  EC  EF  / kT 
N C 10 cm
about 60 mV/decade
3 decades x 60 mV  180 mV  180 meV down