* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Moments of INERTIA
Mitsubishi AWC wikipedia , lookup
Coriolis force wikipedia , lookup
Classical mechanics wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Fictitious force wikipedia , lookup
Centrifugal force wikipedia , lookup
Hunting oscillation wikipedia , lookup
Jerk (physics) wikipedia , lookup
Moment of inertia wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Accretion disk wikipedia , lookup
Work (physics) wikipedia , lookup
Equations of motion wikipedia , lookup
Seismometer wikipedia , lookup
Center of mass wikipedia , lookup
Classical central-force problem wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Moments of INERTIA
Review of Inertia
• Inertia – Objects with mass always resist a
change in there motion (acceleration). From
Newton’s second law we see that this
resistance depends on the objects’ mass only.
• SF = ma or a = SF/m
• However this concept of inertia applies to
translational does it also apply to rotational
motion?
The “Roll” of Mass
• Let us say there are two wheels, both the same
size, one is made out of a light plastic and the
other heavy lead. If you to spin them, which
would be harder to get to move, and which one
would be harder to stop once it started spinning?
• The answer many would say the lead one and
they would be right, but why?
• Obviously the lead wheel has more mass so it will
have a greater resistance to change.
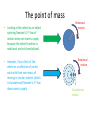
The point of mass
• Looking at the wheel as an object
spinning Newton’s 2nd law of
motion does not seam to apply
because the wheel’s motion is
rotational and not translational.
• However, if you think of the
wheel as a collection of points
each with their own mass all
moving in circular motion (which
is translational) Newton’s 2nd law
does seam to apply
Rotational
motion
Rotational
motion
Translational
motion
The Shape of things
• Who is harder to spin in a circle with a rotational
speed of 1 RPM; a 10 g point moving with a
radius of 20 cm, or a 10 g point moving with a
radius of 1 m?
• Since both points complete 1 circle in the same
amount of time the outside point must travel 5x
faster than the inside point, which means it is
harder to get the outside point to move at the
same angular rate as an inside point.
• So let us say we have to a 1 kg
disk, with a radius of 50 cm,
whose mass is evenly
distributed through from it’s
center to edge. And a 1kg
hoop, with a radius of 50 cm,
that has no mass on the interior
and all of it’s mass is on it’s
edge.
• Which of these two would be
harder to get to spin, and which
would be harder to stop
spinning once they get started?
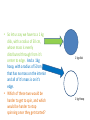
1 kg disk
1 kg Hoop
• There can be no difference due to the quantity
of mass since they both have the same mass.
• However the hoop has all of its mass moving
in the largest possible circle making it a
difficult as possible to change the hoop’s
rotational motion.
• So the difficulty is not just about mass, but
how it is distributed in the object that is
rotating.
• The disk’s mass is spread out meaning it will
be easier to change the rotational motion of
the inter mass since
The sum resistance of each hoop from small to large is Less than the resistance of one large hoop.
Moments of Inertia
• Moments of Inertia is an object’s resistance to
change in it’s rotational motion
– It is how well an objects resists angular
acceleration
– Moments of Inertia play the same roles in
rotational motion as mass does in translational
motion.
Moments of Inertia
• The symbol we use for the Moment of Inertia
is the letter “I”
• The Units for the Moment of inertia are often
Kg*m2
– They are always mass*distance2
• Each shape has it’s own unique equation for
its moment of inertia
– Some examples:
•
•
•
•
I Thin Hoop = Mass*Radius2 = mr2
I Disk = (1/2) Mass*Radius2 = (1/2)mr2
I solid Sphere = (2/5)Mass*Radius2 = (2/5)mr2
I Hollow Sphere = (2/3)Mass*Radius2 = (2/3)mr2
A “rotational version of Newton’s 2nd
Law”
• We know that when an object is pulled by an unbalanced force it
moves in a translational way with an acceleration that is a = SF/m.
But what if the object had an unbalanced torque?
• For example let’s say there is
a wheel that has a fixed axis
in it’s center. And there is
a force that pulls an the rim
of the wheel. (For simplicity
we will ignore gravity)
Radius
(r)
Torque (t)
Fixed axis lets the wheel spin, but
Not translate (holds the wheel in place)
•
The net unbalanced torque cause the rotation of the disk to change
– The net torque creates and angular acceleration (much like a force creates a
translational acceleration)
•
The relationship between the Net torque and angular acceleration is very logical if
you remember the following
– Torques are like forces for the “rotational world”
– Moments of inertia acts like mass for the “rotational motion”
– Accelerations are accelerations
•
So since for translational motion SF = ma
– Or a = SF/m
– The rate of an object’s change in motion is a ratio of the Force’s influence to create
change in translational motion and the object’s ability to resist change
•
Then for rotational motion St = Ia
– Or a= St /I
– The rate of an object’s change in rotational motion is a ratio of the torque’s influence to create
change in rotational motion and the object’s ability to resist change
A “rotational version of Newton’s 2nd
Law”
• Now let’s say there is a wheel that has a fixed axis in it’s center. And there
is a force that pulls an the rim of the wheel. And we want to find the
angular acceleration of the disk. (For simplicity we will ignore gravity)
q
Force (F)
creates the torque
Since St =Ia
And t = [Fsin(q)]r
Radius
(r)
[Fsin(q)]r = Ia
Torque (t)
Created by the force
a = {[Fsin(q)]r}/I
t = Fr = [Fsin(q)]r
Fixed axis lets the wheel spin, but
Not translate (holds the wheel in place)
Remember that for a disk
I = (1/2)mr2
Problem Solving
• Since rotational dynamics follows its own version of Newton’s 2nd Law (like
translational dynamics) we can use pretty much the same strategy
• Step 1: Draw free body diagram
– Done similarly with forces, but here you need to draw the forces where the
act on the object, not just at the object’s center of mass.
• Step 2: Write out the net Force equation, AND torque equation
– Instead of just SF = ma, we also use St = Ia
• Step 3: Find accelerations and Moments of inertia
– Since it is not just the object’s mass, but shape determines how an object
resists a net torque we will normally have to calculate the object’s moment of
inertia.
– We normal will have to find the angular acceleration in the system, sometimes
we will need to relate the object’s angular acceleration to the tangential
acceleration to the object’s surface.
• Step 4: Solve the problem
Single Object same problem
• We have a disk that has a mass of 10 kg and a radius of
.5 meters. A string is wrapped around the disk and
pulled with a constant force of 50N as shown, for a
time of 6 seconds. What is the disk’s final angular
velocity, and what is the tangential speed of the
wheel’s rim?
50 N
30O
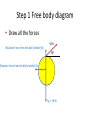
Step 1 Free body diagram
• Draw all the forces
50 N
(Reaction Force from the disk’s holder) Ry
30O
(Reaction Force from the disk’s holder) Rx
Fg = -98 N
Step 1 Free body diagram
• Draw Torques
50 N
(Reaction Force from the disk’s holder) Ry
30O
(Reaction Force from the disk’s holder) Rx
Picking the axial as the pivot.
Fg = -98 N
Notice that all the blue forces
go trough the axils so the
produce no torque.
Step 1 Free body diagram
• Draw and find torques
50 N
60O
30O
.5m
-[(50N Sin(60)).5m)]
or
-[(50N Cos(30)).5m]
Picking the axial as the pivot.
Only the 50N force does not go through the axel so it creates a torque around it.
Step 2 Write the torque equation
50 N
60O
30O
.5m
-[(50N Sin(60)).5m)]
or
-[(50N Cos(30)).5m]
Picking the axial as the pivot.
St = -[(50N Sin(60)).5m)] = Ia
= -[12.5Nm] = Ia
Step 3 Find moments of inertia and/or
accelerations
50 N
60O
30O
.5m
-[(50N Sin(60)).5m)]
or
-[(50N Cos(30)).5m]
Picking the axial as the pivot.
IDisk = (1/2)Mr2 = (1/2)(10kg)(.5m)2
IDisk = 12.5 kgm2
Step 3 Find moments of inertia and/or
accelerations
50 N
60O
30O
.5m
-[12.5Nm]]
Picking the axial as the pivot.
St = Ia
= -[12.5Nm] = [12.5 kgm2]a
a = -1 rad/sec2
Step 3 Find moments of inertia and/or
accelerations
a = (.5m/s2)
.5m
a = -1 rad/sec2
a = ar
a = (1 rad/sec2)(.5m)
Remember we remove the sign
for the acceleration because
rotational language is different
than translational language
Step 4: Solve
Vf = Vi + at
Vf = ( 0m/s) + (.5m/s2)(6s)
Vf = 3m/s
wf = wi + at
wf = ( 0m/s) + (-1 rad/s2)(6s)
wf = -6 rad/s
wf = 6 rad/s clockwise
An Application
• Let us look at a disk that is attached and wrap around
several times by a rope that is also attached to an
object that will fall. The disk has a fixes axel in it’s
center. How can we find the falling objects
acceleration? (Since the object is attached to the disk it
can’t fall freely so the acceleration must be less than
9.8 m/s2.)
Radius = r
Mass = MD
Mass = Mh
Step 1: FBD
Just like all problems where forces are involved we start with a free body diagram.
It is easier to 1st separate the objects and then look at all the forces on the objects.
Fn = The reaction force from
the axel (since it is fixed)
Tension force = FT
Radius = r
Mass = MD
Mass = Mh
Tension force = -FT
Fg = (MD)(-9.8
m/s2)
Fg = (Mh)(-9.8 m/s2)
Step 2: Force equations
Fn = The reaction force from
the axel (since it is fixed)
Tension force = FT
Radius = r
Mass = MD
Mass = Mh
Tension force = -FT
Fg = (MD)(-9.8
m/s2)
Fg = (Mh)(-9.8 m/s2)
SF: Fn + FTension + Fg = (MD)(0 m/s2)
SF: FTension + Fg = (Mh)a
SF: Fn + -FT + (MD)(-9.8 m/s2) = 0 N
SF: FT + (Mh)(-9.8 m/s2) = (Mh)a
Oh no!!
Here we would normally find the acceleration by we can’t just yet. We do not have
enough information. But when faced to a large problem it is often best to torque you
way through it.
SF: Fn + -FT + (MD)(-9.8 m/s2) = 0 N
FT = (MD)(-9.8
m/s2)
+ Fn
SF: FT + (Mh)(-9.8 m/s2) = (Mh)a
FT + (Mh)(-9.8 m/s2) = (Mh)a
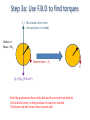
Step 3a: Use F.B.D to find torques
Tension force = FT
Mass = Mh
Fg = (Mh)(-9.8 m/s2)
These forces produce no
Torque on the hanging mass
So we can ignore this.
Step 3a: Use F.B.D to find torques
Fn = The reaction force from
the axel (since it is fixed)
Radius = r
Mass = MD
Tension force = -FT
-FT
Fg = (MD)(-9.8 m/s2)
Both the gravitational force of the disk and the normal force both act
On the disk’s center, so they produce no torque on the disk,
This leaves only the tension force to work with.
Step 3b: Torque equations
Radius = r
Mass = MD
Tension force = -FT
St =(-FT)r = Ia
a = (-FT)r /I
Remember that for a disk
I = (1/2)MDr2
a = (-FT)r /(1/2) MDr2
a = 2(-FT) /MDr
Step 4: relating angular to tangential
Radius = r
Mass = MD
Tension force = -FT
So the torque equation gives us the angular acceleration:
a = 2(-FT) /MDr
We can now relate angular acceleration of the disk to the tangential
acceleration of it’s rim. That tangential acceleration is equal to the acceleration of
the falling object.
a = ar so a =a/r
a/r = 2(-FT) /MDr
a = 2(-FT) /MD
Now we can find acceleration
a = 2(-FT) /MD
FT + (Mh)(-9.8 m/s2) = (Mh)a
(-FT) = (1/2)aMD
(1/2)aMD = (-FT)
(-FT) = (1/2)aMD
(Mh)(-9.8 m/s2) = (Mh)a + (1/2)aMD
(Mh)(-9.8 m/s2) = a[(Mh) + (1/2)MD]
[(Mh)(-9.8 m/s2)]/ [(Mh) + (1/2)MD] = a