* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download slides
Survey
Document related concepts
Exact cover wikipedia , lookup
Knapsack problem wikipedia , lookup
Birthday problem wikipedia , lookup
Lateral computing wikipedia , lookup
Computational complexity theory wikipedia , lookup
Corecursion wikipedia , lookup
Pattern recognition wikipedia , lookup
Smith–Waterman algorithm wikipedia , lookup
Travelling salesman problem wikipedia , lookup
Simplex algorithm wikipedia , lookup
Algorithm characterizations wikipedia , lookup
Fast Fourier transform wikipedia , lookup
Expectation–maximization algorithm wikipedia , lookup
Genetic algorithm wikipedia , lookup
Planted motif search wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
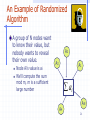
Transcript
Randomized Algorithms 1 Upper Bounds We’d like to say “Algorithm A never takes more than f(n) steps for an input of size n” “Big-O” Notation gives worst-case, i.e., maximum, running times. A correct algorithm is a constructive upper bound on the complexity of the problem that it solves. 2 Lower Bounds Establishe the minimum amount of time needed to solve a given computational problem: Searching a sorted list takes at least O(log N) time. Note that such arguments also classify the problem; need not be constructive! 3 Randomized vs Deterministic Algorithms Deterministic algorithms Take at most x steps Assuming input distribution, analyze expected running time. Randomized algorithms Take x steps on average Take x steps with high probability Output “correct” answer with probability p 4 Randomized Quicksort Always output correct answer Takes O(N log N) time on average Likelihood of running O(N log N) time? Running time is O(N log N) with probability 1-N^(-6). 5 Order Statistics The ith order statistic in a set of n elements is the ith smallest element The minimum is the 1st order statistic The maximum is the nth order statistic The median is the n/2th order statistic If n is even, there are 2 medians How can we calculate order statistics? What is the running time? 6 Order Statistics How many comparisons are needed to find the minimum element in a set? The maximum? Can we find the minimum and maximum with less than twice the cost? Yes: Walk through elements by pairs Compare each element in pair to the other Compare the largest to maximum, smallest to minimum Total cost: 3 comparisons per 2 elements, 3n/2 comparisons in total 7 Finding Order Statistics: The Selection Problem A more interesting problem is selection: finding the ith smallest element of a set We will show: A practical randomized algorithm with O(n) expected running time A cool algorithm of theoretical interest only with O(n) worst-case running time 8 Randomized Selection Key idea: use partition() from quicksort But, only need to examine one subarray This savings shows up in running time: O(n) q = RandomizedPartition(A, p, r) A[q] p A[q] q r 9 Randomized Selection RandomizedSelect(A, p, r, i) if (p == r) then return A[p]; q = RandomizedPartition(A, p, r) k = q - p + 1; if (i == k) then return A[q]; if (i < k) then return RandomizedSelect(A, p, q-1, i); else return RandomizedSelect(A, q+1, r, i-k); k A[q] p A[q] q r 10 Randomized Selection Analyzing RandomizedSelect() Worst case: partition always 0:n-1 = T(n-1) + O(n) = ??? = O(n2) (arithmetic series) No better than sorting! T(n) “Best” case: suppose a 9:1 partition = T(9n/10) + O(n) = ??? = O(n) (Master Theorem, case 3) Better than sorting! T(n) What if this had been a 99:1 split? 11 Randomized Selection Average case For upper bound, assume ith element always falls in larger side of partition: n 1 1 T n T max k , n k 1 n n k 0 2 n 1 T k n n k n / 2 What happened here? Let’s show that T(n) = O(n) by substitution 12 Randomized Selection Assume T(n) cn for sufficiently large c: T ( n) 2 n 1 T (k ) n n k n / 2 The recurrence we started with 2 n 1 ck n n k n / 2 n 2 1 2c n 1 k k n n k 1 k 1 2c 1 1n n Expand arithmetic series n 1n 1 n What happened here? n 2 2 2 2 cn cn 1 1 n 2 2 What happened Substitute T(n) here? cn for T(k) What happened here? “ Split” the recurrence Multiply it out here? What happened 13 Randomized Selection Assume T(n) cn for sufficiently large c: T ( n) cn cn 1 1 n 2 2 cn c cn c n 4 2 cn c cn n 4 2 cn c cn n 4 2 cn (if c is big enough) The recurrence so far What happened Multiply it out here? What happened Subtract c/2 here? Rearrange the arithmetic What happened here? What we set out here? to prove happened 14 Worst-Case Linear-Time Selection Randomized algorithm works well in practice What follows is a worst-case linear time algorithm, really of theoretical interest only Basic idea: Generate a good partitioning element Call this element x 15 Worst-Case Linear-Time Selection The algorithm in words: 1. Divide n elements into groups of 5 2. Find median of each group (How? How long?) 3. Use Select() recursively to find median x of the n/5 medians 4. Partition the n elements around x. Let k = rank(x) 5. if (i == k) then return x if (i < k) then use Select() recursively to find ith smalles element in first partition else (i > k) use Select() recursively to find (i-k)th smallest element in last partition 16 Worst-Case Linear-Time Selection How many of the 5-element medians are x? At least 1/2 of the medians = n/5 / 2 = n/10 How many elements are x? At least 3 n/10 elements For large n, 3 n/10 n/4 (How large?) So at least n/4 elements x Similarly: at least n/4 elements x 17 Worst-Case Linear-Time Selection Thus after partitioning around x, step 5 will call Select() on at most 3n/4 elements The recurrence is therefore: T (n) T n 5 T 3n 4 n n/5 ??? n/5 T n 5 T 3n 4 n cn 5 3cn 4 (n) Substitute T(n) =??? cn 19cn 20 (n) Combine fractions ??? Express in desired form ??? cn cn 20 n ??? cn if c is big enough What we set out to prove 18 Worst-Case Linear-Time Selection Intuitively: Work at each level is a constant fraction (19/20) smaller Geometric progression! Thus the O(n) work at the root dominates 19 Selection Algorithm Using sorting, takes O(nlogn) time A randomized algorithm Takes O(n) time on average Takes O(n) time with high probability A deterministic algorithm Takes O(n) time 20 An Example of Randomized Algorithm A group of N nodes want to know their value, but nobody wants to reveal their own value. Node Ai’s value is ai We'll compute the sum mod m, m is a sufficient large number A2 A3 A1 ai A4 AN 21 An Example of Randomized Algorithm – the protocol Node Ai chooses N-1 random numbers X1i, X2i, ..., XN-1i in the range 0,...,M-1 and a number pi ai ( x1i ... xii1 xii1 ... xNi 1 p i ) mod m Each node Ai distributes the N-1 Xji to the N-1 other nodes and keeps the number pi to his own Each node computes si like this si ( xi1 ... xii 1 xii 1 ... xiN 1 p i ) mod m Each node Ai distributes the si to others All nodes can know the sum by (i 1 s i ) mod m N 22 Many Other Randomized Algorithms Hashing: Universal Hash Function Resource Sharing Ethernet collision avoidance Load Balancing Packet Routing Primality Test 23