* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Foundations
Meaning (philosophy of language) wikipedia , lookup
Modal logic wikipedia , lookup
Mathematical logic wikipedia , lookup
Quantum logic wikipedia , lookup
Intuitionistic logic wikipedia , lookup
Tractatus Logico-Philosophicus wikipedia , lookup
Bernard Bolzano wikipedia , lookup
Laws of Form wikipedia , lookup
Axiom of reducibility wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Natural deduction wikipedia , lookup
Halting problem wikipedia , lookup
Analytic–synthetic distinction wikipedia , lookup
History of the function concept wikipedia , lookup
Law of thought wikipedia , lookup
Propositional calculus wikipedia , lookup
Propositional formula wikipedia , lookup
Discrete Mathematics
Chapter 1.
The Foundations
Cheng-Chia Chen
Transparency No. 1-0
The Foundations
1. The foundations
Logic:
The basis of all mathematical reasoning
has practical applications to the design of
computing machine
give the precise meaning of math. statements.
Sets:
The basis of all mathematical structures.
definitions, operations
Functions :
definitions, classification, operations
Transparency No. 1-2
The Foundations
1.1 Logic
Proposition:
A statement that is either true or false (,but not
both).
Example:
1. Taipei is the capital of ROC. 2. Tokyo is the capital of Korea.
3. 1+1 = 2. 4. 2+2 = 3.
5. There is no integer x,y,z and n > 2 s.t.
xn + yn = zn ---- Fermat’s last theorem
6. “Every even number is the sum of two prime numbers.” ---Goldaach’s conjecture (1742)
==>
1. Statement (1)~(5) are propositions,
2. (1),(3) are true; (2),(4) are false.
3. Nobody knew (5) is true or false until 1994, but it must be
true or false, hence it is a proposition. (6) open problem.
Transparency No. 1-3
The Foundations
More Examples
Examples:
1. What time is it? (interrogative)
2. Read this carefully! (command)
3. x+1 = 2.
4. x+y = z.
==>
1. (1) and (2) are not statements
2. (3) and (4) are not propositions:
neither true nor false!
Transparency No. 1-4
The Foundations
Propositional variables and propositional constants
In algebra, we use variables to denote an item with
unspecified value.
e.g. 10 chickens and rabbits in a cage with 16 feet. ==>
#rabbits = ? and #chickens=?
==> let x = #rabbits, y = #chickens
==> x + y = 10 /\ 2x + 4y = 16.
Likewise, In logic, we can use propositional variable
to denote an arbitrary proposition with unspecified
truth value.
e.g., If it is raining, the ground is wet. since the ground is
wet, it is raining now.
==> Let p =def “It is raining”, q =def “the ground is wet”
==> ((p ->q) /\ q) -> p.
Propositional constants: only two values:
T(true), F(false).
Transparency No. 1-5
The Foundations
Forming Compound propositions from simpler ones
Primitive propositions:
propositional variables
propositional constants
P, Q: two known propositions
Then the followings are also propositions:
1. “P and Q” : ( P /\ Q) conjunction of P and Q
2. “It is not the case that p”: (~P) negation of P
3. “P or Q” : (P \/ Q) disjunction of P and Q
4. “P implies Q” : ( P Q) implication
P : antecedent, premise, hypotheses;
Q: consequence, conclusion
equivalent phrase:
– “P entails Q”, “Q if P”, “P only if Q”
5. “p iff q” (p <->q) equivalence of P and Q
Transparency No. 1-6
The Foundations
Truth conditions for compound propositions
1.
2.
3.
4.
5.
P /\ Q is true iff both P and Q are true
P \/ Q is true iff either P or Q is true
~P is true iff P is not true (i.e., false)
P<->Q is true iff both are true or both are false.
PQ is true iff whenever P is true, Q is true
( i.e., it is not the case that P is true but Q is false )
In the propositions, /\, \/, <-> and are called binary
connectives(or operations) and ~ is called unary
connective(or operations).
Other binary connectives are possible.
What about the truth condition for primitive
propositions?
Transparency No. 1-7
The Foundations
From natural language statements to formal logic expressions
Natural language statement
Today is Friday
I have a test today
It is not the case that today is
Friday
Today is not Friday
Today is Friday and
I have a test today
If today is Friday, then I have
a test today.
Today is Friday or I have a
test today.
symbolized logic expr.
p
q
~p
~p
(P ∧ q)
(pq)
(P ∨ q)
Transparency No. 1-8
The Foundations
Truth conditions for propositions
Problem: when will you say that the sentence:
It_is_raining
is true ?
=> The proposition:” It_is_raining” is true if the meaning
(or fact) that the proposition is intended to represent
occurs(happens, exists) in the situation that the
sentence referred to.
=>Example: Since it is not raining now(the current situation), the
statement It_is_raining is false (in the current situation). But if
it were raining now, then I would say that It_is_raining is true.
Factors affecting the truth value of a proposition:
the situation in which the proposition is used.
the meaning of the proposition.
Transparency No. 1-9
The Foundations
Truth table
•The meaning of logical connectives can be
represented by a truth table.
A
B
~A
A/\B
A\/B
A->B
A<->B
0
0
1
0
0
1
1
0
1
1
0
1
1
0
1
0
0
0
1
0
0
1
1
0
1
1
1
1
Transparency No. 1-10
The Foundations
Other usual connectives
Besides /\,\/, and <->, there are also some other
connectives as you have known in digital system.
xor , nand, nor.
Rules: let I(x) denote the truth value of x.
I(A B)= I(~(A<->B))=1 iff not I(A)=I(B)
I(A nand B) = I(~(A/\B)).
I(A nor B) = I(~( A \/B)).
Transparency No. 1-11
The Foundations
1.2 Propositional Equivalence
Some definitions: Let A be any proposition,
then
1. A is a tautology(contradiction) iff A is true
(false) no matter what the truth values of the
prop. variables inside A are given.
2. If A is neither a tautology nor a
contradiction, then A is called a contingency.
Contingencies
Tautologies
(valid)
Contradictions
(unsatisfiable)
The geography of propositions
Transparency No. 1-12
The Foundations
Logical Equivalence
A and B are logically equivalent (,A B) if A <-> B is a
tautology
Theorem1: Logical equivalence relation is reflexive,
symmetric and transitive.
I.e., for all propositions A,B and C,
1. A A
2. A B implies B A and
3. A B and B C imply A C.
Theorem2[substitution theorem]: If A B and C[X] is
a proposition containing X as a subproposition, then
C[A] and C[B] are logically equivalent, where C[A] is
the result of C with X in C replaced by A.
ex: (p∨q) (q∨p), C[X] =def ~(p ∧ X)
=> ~(p∧ (p∨q) )~(p∧ (q∨p))
Transparency No. 1-13
The Foundations
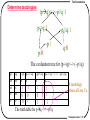
Determine tautologies, contradictions and contingencies
Problems: Given a proposition A, how can you determine
whether it is a tautology, a contradiction or a contingency?
=>Exhausted evaluation! (by using truth table)
e.g., A = (p->q) <-> (~p \/q) a tautology ?
1. there are two primitive props: p, q.
2. So there are 4 possible assignments of truth values to p
and q.
p=0,q=0: p=0,q=1:
p=1,q=0:
p=1,q=1:
3. Under each assignment, we can evaluate the truth value of
A (in bottom up way) by the truth condition rule of
connecting connectives.
Transparency No. 1-14
The Foundations
Determine tautologies
(pq)<->~p\/q :1
p->q:1
~p:1
p:0
~p \/q:1
q:0
The evaluation tree for (p->q)<-> (~p\/q)
p
q
~p p->q
~p\/q
p->q <-> ~p\/q
0
0
1
1
1
0
1
1
1
T
1
0
0
1
1
0
1
1
1
0
1
0
1
1
1
The truth table for pq <-> ~p\/q
A tautology
since all are 1’s
Transparency No. 1-15
The Foundations
Determine other properties
1. logical equivalence: A <=> B iff A<->B is a tautology.
So we can apply the procedure for determining
tautology to determine if A <=>B.
2. contradiction: A is a contradiction iff ~A is a
tautology
3. Satisfiability: A is satisfiable iff ~A is not a tautology.
4. contingence: A is a contingence iff neither A nor ~A
is a tautology.
5. logical consequence: B is a logical consequence of
A [denoted A |= B] iff AB is a tautology.
Transparency No. 1-16
The Foundations
Some important logical equivalences
P /\ T P
P/\P P
• Identity law
•Idempotent law
P \/ F P
P\/P P
P \/ T
• Domination law
P /\ F
~(~P)
• Double negation
P \/ Q
•Commutative
P /\ Q
P \/ (Q \/ R)
•Associative
P /\ (Q /\ R)
==> P /\ (Q /\ R) = (P/\Q/\R)
P /\(Q \/ R)
•Distribution law
P \/(Q /\ R)
~(P /\Q)
•DeMorgan’s law
~(P\/Q)
==> ~(P1 /\ P1/\.../\Pn)
Transparency No. 1-17
The Foundations
One Example:
Show that
~(p \/ (~p /\ q) ~p /\ ~q
Proof:
1. By truth table (omitted)
2. ~(p \/ (~p /\ q) deM
~p /\ ~(~p /\ q) deM
~p /\ (~(~p) \/ ~q) DbNeg
~p /\ (p \/ ~q) Distr
(~p \/ ~q) /\ (~p \/ p) ExMd
(~p \/ ~q) \/ T identity
(~p \/ ~q)
Transparency No. 1-18
The Foundations
1.3 Predicates (述詞) and quantifiers(量詞)
Problems of Propositional logic:
Cannot analyze the content of primitive
propositions.
cannot group similar propositions
cannot analyze quantifiers.
Ex: Consider the following situations:
1. Family = {a,b,c1,c2,c3 }
2. We are interested in who is whose
brother.
3. Suppose In Family, ci is cj’s brother if i
j for i,j =1..3.
Transparency No. 1-19
The Foundations
Inadequancy of propositional logic
Primitive propositions needed:
x_is_y’s_brother, x,y Family
So we need 25 propositions.
New approach: Parameterized
proposition(Predicate).
Use a (predicate) symbol B to symbolize the
statement:
B(x,y) x is y ‘s brother.
e.g.,
B(a,c1) : a is c1’s brother,
B(c2,c2) : c2 is c2’s brother,
...
Transparency No. 1-20
The Foundations
Benefits of Predicates
Advantage of using predicates:
==>
1. need only 6 (1 predicate and 5 names)
symbols.
2. can group related propositions together.
(B(x,y) and others, for instance,
q(x) x_is_old. )
3.The most important : allow representation of
quantified statement like: c1_has_a_brother (or,
there is an object x which is c1’s brother, $ x B(x, c1))
to be inferred from
c2_is_c1’s brother ( B(c2,c1) )
Transparency No. 1-21
The Foundations
Predicates
In the expression:
B(x,y )
B : predicate symbol (or proposition function)
x (y) : first (2nd) argument
B(x,y) : [atomic] proposition(or formula)
#arguments in B(X,Y): the arity of the predicate
symbol B.
Notes:
1. Each arity has a fixed arity.
2. B(x,y,c1) and B(x) are meaningless.
because used #arguments different from B’s arity.
Transparency No. 1-22
The Foundations
Predicates (cont’d)
3. The truth value of a proposition p(x1,...,xn)
depends on both p and x1,...,xn.
Ex1: Let p(x) “x >3 “. then
P(4) “4 > 3” has truth value T,
P(2) “2 > 3” has truth value F.
Ex2: Let Q(x,y) “x = y +3” then
Q(1,2) = “1 = 2 + 3” is false.
Q(3,0) = “3 = 0 + 3” is true.
Mathematically, we can define (the meaning of) P as a
function [P]
[P]: Un (n is P’s arity) --> {T,F}with the intention that
“P(x1,...,xn)” holds (is true) iff [P]([x1],...,[xn]) = T.
Transparency No. 1-23
The Foundations
Set representations of truth-functions
Ex:
[B]: Family2 -->{T,F} s.t. [b](x,y) = T iff x =[ci], y=[cj], i j.
p(x) “x >3 “ , So [P]: N --> {T,F } s.t. [P](x) = T iff x > 3.
Q(x,y) “x = y +3” , so
[Q] : N2 --> {T,F} with
[Q](x,y) = T iff x = y +3.
Note: P partition N into two sets, one with members
So, instead of represent
mapped to T and one mapped to F.
P(x) = T.
P as a truth function, we
equivalently represent P
{1,2,3}
{4,5,...}
as the set {x | P(x) = T }
= {4,5,6,...}
P(x) = F
Similarly, we can represent Q as {(x,y) | x = y + 3 }
N
Transparency No. 1-24
The Foundations
constant, function, variables and terms
In the statement:
“y > min(x, 3)” --- (s1)
x,y are called variables,
3 is a constant,
min is a function symbol with arity 2
“min(3,2)” behaves more like x, 3 than “x >y”.
So if let P(x,y) “x > y”, then
s1 can be represented as
P(y, min(x,3))
we call any expression that can be put on the
argument position of an atomic proposition a term
Obviously, constants and variables are terms;
moreover,if f is a function of arity n, and t1,...tn are n terms,
then so is f(t1,...,tn).
Transparency No. 1-25
The Foundations
Universal and existential quantifications
A: any statement (or called formula)
e.g., A = p(x,y) /\ q(x,f(3)),...
x: any variable,
Then
1. ("x A) is a new formula called the universal
quantification of A,
2. ("x A) means:
“A(x) is true for all values of x in the universe of
discourse.”
3. ($x A) is a new formula called the existential
quantification of A,
4. ($x A) means:
“A(x) is true for some value of x in the universe of
discourse.”
Transparency No. 1-26
The Foundations
Quantifiers and universe of discourse
Consider the sentence: p(x) = “x > 0”.
1. as stated before, p(x) is true or false depending on
the value of x.
2. p(1), p(2),... : true;
p(0) , p(-1),...: false
Universe of Discourse (U,論域):
The set of objects (domain) from which all variables
are allowed to have values.
Ex: consider the sentence:
s2: ”all numbers are greater than 0”.
(for-all x “x > 0” ) or (" x p(x) )
U = N+={1,2,3,...} => s2 is true. U = Z={...,-1,0,1,...}=>
s2 is false.
Transparency No. 1-27
The Foundations
Translation of NL statement into logical one
Translate the following sentences into logical
expressions:
1. Every body likes Chang
2. Everybody loves somebody.
3. There is somebody loved by every one.
4. Nobody likes everybody.
5.There is somebody Chang don’t like.
6. there is somebody no one likes.
7.there is exactly one person everybody likes.
8 Chang likes exactly two persons
9. Everyone likes himself.
10. There is someone who likes no one who does not
like himself.
Transparency No. 1-28
The Foundations
Terminology about formulas
Occurrences of variables in formulas:
A = p(f(x), c) \/ q(x,y)
A contains 2 variables, one of which occurs
twice.
Free and bound variables:
A: a formula
fv(A) = the set of all free variables in A is defined as
follows:
If A is atomic => fv(A) is the set of all variables
in A
fv(~A) = fv(A)
fv(A/\B)=fv(A\/B)=fv(A->B)=fv(A<->B)= fv(A) U
fv(B).
fv( for-all x A) = fv($xA) = fv(A)\ {x}.
Transparency No. 1-29
The Foundations
bd(A): the set of bound variables in A is defined as
follows;
1. If A is atomic => bd(A) = {}
2. bd(~A) = bd(A)
3. bd(A/\B) = d(A\/B) = bd(AB)
=bd(A<->B) = bd(A) U bd(B).
4. bd( ∀x A) =
bd(A) if x ∉ fv(A).
bd(A) U {x} if x ∈ fv(A).
Example A = ($ x p(x,y)) \/ q(x)
=> fv(A) = {x,y}; bd(A) = {x}
x occurs twice in A, one occurs free and the other
occurs bound.
Def: A is a sentence iff fv(A) = {}
Note: A is a proposition if A is a sentence
Transparency No. 1-30
The Foundations
More logical notions [omitted!!]
A B [logical equivalence (in predicate logic)]
iff A <-> B is a tautology(or valid) for all possible values
of free variables in A and in B.
Common equivalences:
1. all propositional equivalences
A->B ~A \/ B,
~~A A, ~(A/\B) ~A\/~B,...
2. ~ "x A < $x ~A.
3. ~$xA "x ~A.
4. "x (A /\ B) "x A /\ "xB.
5. $x(A \/B) $xA \/ $XB
If x is not free in B, and Q is " or $, then
6 Qx (A /\ B) QxA /\ QxB
7. Qx(A\/B) QxA \/ QxB
Transparency No. 1-31
The Foundations
1.4 Sets
Basic structure upon which all other (discrete and
continuous ) structures are built.
a set is a collection of objects.
an object is anything of interest, maybe itself a set.
Definition 1.
A set is a collection of objects.
The objects is a set are called the elements or
members of the set.
If x is a member of a set S, we say S contains x.
notation: x S vs x S
Ex: In 1,2,3,4,5, the collection of 1,3 5 is a set.
Transparency No. 1-32
The Foundations
Set description
How to describe a set:?
1. List all its member.
the set of all positive odd integer >10 = ?
The set all decimal digits = ?
the set of all upper case English letters = ?
The set of all nonnegative integers
=?
2. Set builder notation:
P(x) : a property (or a statement or a proposition)
about objects. e.g., P(x) = “ x > 0 and x is odd”
then {x | P(x) } is the set of objects satisfying
property P.
P(3) is true => 3 {x | P(x)}
P(2) is false => 2 {x | P(x)}
Transparency No. 1-33
The Foundations
Conventions
N =def {x | x is a natural numbers } = { 0,1,2,3,...}
N+ =def {1,2,3,...}
Z =def {...,-3,-2,-1,0,1,2,3,...}
R =def the set of real numbers.
Problem:
The same set may have many different descriptions.
{x | 0 < x <10 /\ x is odd }
{1,3,5,7,9}, {5,3,1,9,7}
{9,7,1,3,5}.
Transparency No. 1-34
The Foundations
Set predicates
Definition 2.
Two sets S1, S2 are equal iff they have the
same elements
S1 = S2 iff "x (x S1 <-> x S2)
Ex: {1,3,5} = {1,5,3} = {1,1,3,3, 5}
Graphical representation of sets:
Venn Diagrams:
rectangle: Universal set: U
circles: sets
points: particular elements
point x inside circle S => x S
point x outside S => x S.
Transparency No. 1-35
The Foundations
Set predicates (cont’d)
Null set ={} = =def the collection of no objects.
Def 3’: [empty set] for-all x x .
Def 3. [subset]
A B iff all elements of A are elements of B.
A B for-all x (x A ⇒ x B)).
Def 3’’: A B =def A B /\ A B.
Exercise : Show that:
1. For all set A (
2. (A B /\ B A) (A = B)
3. A
Diagram representation of the set inclusion
relationship.
Transparency No. 1-36
The Foundations
Size or cardinality of a set
Def. 4: | A | = the size(cardinality) of A = # of distinct
elements of A.
Ex:
|{1,3,3,5}| = ?
|{}| = ?
| the set of binary digits } | = ?
|N| = ? ; |Z| = ? ; | {2i | i ∈ N} = ?
|R| = ?
Def. 5.
A set A is finite iff |A| is a natural number ; o/w it is
infinite.
Two sets are of the same size (cardinality) iff there
is a 1-1 & onto mapping between them.
Transparency No. 1-37
The Foundations
countability of sets
Exercise: Show that
1. |N| = |Z | = | Q | = |{4,5,6,...}|
2. |R| = | (-1, 1) | = |(0,1)|
3. |(0,1)| is uncountable
Def.
A set A is said to be denumerable iff |A| = |N|.
A set is countable iff either |A| = n for some n
in N or |A| = |N|.
By exercise 1,2,3,
R is not countable.
Q and Z is countable.
Transparency No. 1-38
The Foundations
The power set
Def 6.
If A is a set, then the collection of all subsets
of A is also a set, called the poser set of A and
is denoted as P(A) or 2A.
Ex:
P({0,1,2}) = ?
P({}) = ?
|P({1,2,..., n})| = ?
Order of elements in a set are
indistinguishable. But some sometimes we
need to distinguish between (1,3,4) and
(3,4,1) --> ordered n-tuples
Transparency No. 1-39
The Foundations
Show that |A| ≠ |2A|
Pf: (1) The case that A is finite is trivial since |2A| =
2|A| > |A|
and there is no bijection b/t two finite sets with
different sizes.
(2) assume |A| = |2A|, i.e., there is a bijection f: A -> 2A.
Let D = {x ∈ A | x f(x) }. ==>
1. D is a subset of A; Hence
2. $y ∈ A s.t. f(y) = D.
Problem: Is y D ?
if yes (i.e., y D) ==> y f(y) = D, a contradiction
if no (i.e., y D) ==> y f(y) =D, a contradiction too.
So the assumption is false, i.e., there is no bijection
b/t A and 2A.
Transparency No. 1-40
The Foundations
The Halting Problem
L : any of your favorite programming languages (C,
C++, Java, BASIC, etc. )
Problem: write an L-program HALT(P,X), which takes
another L-program P(-) and string X as input, and
HALT(P,X) returns true if P(X) halts and
returns false if P(X) does not halt.
P
Pr(x:String) {
…..
}
“It’s a test …”
X
Program you
are asked to
design
HALT(P,X)
P(X) Halt ?
yes
true
no
false
Transparency No. 1-41
The Foundations
Halt(P,X) does not exist
Motivations of the proof:
Problem1 : What about the truth value of the sentence:
L: L is false
Problem 2 : Let S = {X | X X}. Does S belong to S or
not ?
The analysis: S S => S S; S S => S S.
Conclusion:
1. S is not a set!!
2. If a language is too powerful, it may produce expressions
that is meaningless or can not be realized.
Question: If HALT(P,X) can be programmed, will it
incur any absurd result like the case of S?
Ans: yes!!
Transparency No. 1-42
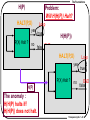
H(P) : Another program using HALT(-,-) as a
subroutine
The Foundations
H(P)
HALT(P,X)
P
yes
P
Pr(x:String) {
…..
}
Loop
P(P) Halt ?
no
true
false
END
P
Note: H(P) Halts iff HALT(P,P) returns false iff P(P) does not halt.
Transparency No. 1-43
The Foundations
H(P)
Problem:
Will H(H(P)) Halt?
HALT(P,X)
yes
P(X) Halt ?
Loop
true
H(H(P))
no false END
HALT(P,X)
yes
P(X) Halt ?
H(P)
no
Loop
true
END
false
The anomaly :
H(H(P) halts iff
H(H(P)) does not halt.
Transparency No. 1-44
The Foundations
Cartesian Products
Def. 7 [n-tuple]
If a1,a2,...,an (n > 0) are n objects, then “(a1,a2,...,an)”
is a new object, called an (ordered) n-tuple [ with
ai as its ith element. ]
Any ordered 2-tuple is called a pair.
(a1,a2,...,am) = (b1,b2,...,bn) iff
(1) m = n and (2) for i = 1,..,n ai = bi.
Transparency No. 1-45
The Foundations
Cartesian product
Def. 8: [Cartesian product]
A x B =def {(a,b) | a ∈ A and b ∈ B }
A1 x A2 x ...x An =def {(a1,...,an) | ai ∈ Ai }.
Ex: A = {1,2}, B = {a,b,c} , C = {0,1}
1. A x B = ? ; 2. B x A = ?
3. A x {} = ? ;4. A x B x C = ?
problem: 1. when will A x B = B x A ?
2. |A x B | = ?
Transparency No. 1-46
The Foundations
1.5 Set operations
union, intersection,difference , complement,
Definition.
1. A B = {x | x ∈ A or x ∈ B }
2. A B = {x | x ∈ A and x ∈ B }
3. If A B = {} => call A and B disjoint.
4. A - B = {x | x ∈ A but x ∉ B }
5. ~ A = U - A
Venn diagram representations
Ex: U = {1,..,10}, A = { 1,2,3,5,8}
B = {2,4,6,8,10}
=> A B , A B , A - B , ~ A = ?
Transparency No. 1-47
The Foundations
Set identities
Identity laws:
A??=A
Domination law: U ? ? = A; {} ?? = {}
Idempotent law: A ? A = A ;
complementation: ~~A = A
commutative :
Associative:
Distributive:
DeMoregan laws:
A?B=B?A
A ? (B ? C) = (A ? B ) ? C
A ? (B ? C) = ?
~(AUB) = ?; ~(A ⋂ B)=?
Transparency No. 1-48
The Foundations
Prove set equality
1. Show that ~(A B) = ~A ~B by show that
1. ~(A B) ~A ~B
2. ~A ~B ~(A B)
pf: (By definition) Let x be any element in ~(A
B) ...
2. show (1) by using set builder and logical
equivalence.
3. Show distributive law by using membership
table.
4. show ~(A (B C)) = (~C ~B) ~A by set
identities.
Note the similarity between logical equivalence and
set identities.
Transparency No. 1-49
The Foundations
Generalized set operations
Def. 6
A1,A2,...An: n sets
B = {A1,A2,...An }
.n {i=1,..n} Ai =def ?
.n {i=1,..n} Ai=def ?
quiz: if B = {} => = ?;
Venn diagram representation of and
.
Example:
{0,,4,6,8},{0,,,,4},C{0,,6,9}>
= ?
Transparency No. 1-50
The Foundations
Set representation
(in computer)
Unordered list or array
union, intersection, ~: time consuming.
Bit string:
U = {a1,...,an} is the universal set.
A: any subset of U
A can be represented by the string:
s(A) = x1 x2 x3....xn where
xi = 1 if a1 ∈ A and 0 o/w.
fast set operations
suitable only if U is not large.
constant size representation.
Transparency No. 1-51
The Foundations
1.6 Functions
Def. 1 [functions]
A, B: two sets
1. a function f from A to B is a set of pairs (x, y) ∈ AxB
s.t., for each x ∈ A there is at most one y ∈ B s.t. (x,y) ∈
f.
2. if (x,y) ∈ f, we write f(x) = y.
3. f :A B means f is a function from A to B.
Def. 2. If f:A B then
1. A: the domain of f; 2. B: the codomain of f
if f(a)=b =>
3. b is the image of a 4. a is the preimage of b
5. range(f) = ?
6. preimage(f) = ?
7. f is total iff ?
Transparency No. 1-52
The Foundations
Types of functions
Def 4.
f: A x B; S: a subset of A,
T: a subset of B
1. f(S) =def ?
2. f-1(T) =def ?
Def. [1-1, onto, injection, surjection, bijection]
f: A -> B.
f is 1-1 (a injection) iff ?
f is onto (surjective, a surjection) iff ?
f is 1-1 & onto <=> f is bijective (a bijection, 1-1
correspondence)
Exercise:Show that if there are onto mappings from A
to B and from B to A, then |A|=|B|.
Transparency No. 1-53
The Foundations
Real valued functions
F:A B is a real valued function iff A and B
are subsets of R.
f1,f2: real valued functions
=> 1. f1+f2 (x) = ?
2. f1• f2 (x) = f1(x) x f2(x).
3. f is increasing iff ?
4. f is strictly increasing iff ?
Transparency No. 1-54
The Foundations
operations on functions
A, B, C: any sets ; f: A B; g: B C, then
1. [identity function]
idA : A A s.t. idA(x) = x for all x in A.
2. [composition of g and f]
gf: A C s.t. gf(x) = g(f(x)) for x in A.
3. [inverse] If f is a bijection, then
f-1: B A s.t. f-1(y) = x iff f(x) = y for y in B.
Graphical representations
Transparency No. 1-55
The Foundations
Properties of operations on functions
f: A B. g: B C; h: C D,
then
1. idA f = f = f idB
2. f(gh) = (fg) h --- assoc.
3. (fg)-1 = g-1 f-1
If f: A A is a bijection then
4. f f-1 = f-1 f= idA .
Sequence:
finite A-sequence: a: [n] (or [1,n]) A
w A-sequence: a : N (or N+) A.
B indexed A-sequence : f:BA.
Transparency No. 1-56
The Foundations
The growth of functions
Summation rules
S ai =def a1 + a2+...an+ (...)
a + (a+d) + (a+2d)+... = ?
a + ar +arr + ... = ?
The growth of functions:
If f is a positive valued function, then what do
the following terms mean?
O(f) means ? o(f) means ?
W(f) means ? w(f) means ?
Q(f) means ?
useful in the analysis of the efficiency of
computer algorithms.
Transparency No. 1-57
The Foundations
Problem, algorithm and Complexity
A problem is a general question:
description of parameters [input]
description of solution[output]
An algorithm is a step by step procedure to
solve a problem.
a recipe
a computer program
We want the most efficient algorithm
fastest (mostly)
most economical with memory (sometimes)
expressed as a function of problem size
Transparency No. 1-58
The Foundations
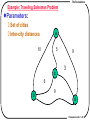
Example: Traveling Salesman Problem
Parameters:
Set of cities
Inter-city distances
a
10
5
c
9
3
6
b
9
d
Transparency No. 1-59
The Foundations
Solution [output]
Solution:
The shortest tour passing all cities
Example: a,b,d,c,a has length 27
a
10
5
c
9
3
6
b
9
d
Transparency No. 1-60
The Foundations
Problem Size
What is appropriate measure of problem
size?
m nodes?
m(m+1)/2 distances?
Use an encoding of the problem
alphabet of symbols: a,b,c,d,0-9, |.
strings: abcd||10|5|9|6|9|3.
Measures
Problem Size: length of encoding.
Time Complexity: how long an algorithm takes,
as function of problem size.
Transparency No. 1-61
The Foundations
Time Complexity
What is tractable?
A function f(n) is O(g(n)) whenever
∃ c > 0 ∃ n0 > 0 s.t. |f(n)| ≤ c ∙ |g(n)| for all n > n0.
A polynomial time algorithm is one whose time
complexity is O(p(n)) for some polynomial p(n).
An exponential time algorithm is one whose
time complexity cannot be bounded by a
polynomial
(e.g., nlog n ).
Transparency No. 1-62
The Foundations
Tractability
Basic distinction:
polynomial time = tractable
exponential time = intractable
execution time in microseconds(μs)
10
20
30
40
50
60
n
.00001s .00002s .00003s .00004s .00005s
.00006s
n2
.0001s
.0004s
.0009s
.0016s
.0025s
.0036s
n3
n5
2n
.001s
.1s
.001s
.008s
3.2s
1.0s
.027s
24.3s
17.9s
.064s
1.7 m
12.7d
.125s
5.2 m
35.7 y
.216s
13.0 m
366c
3n
.059 s
58 m
6.5 y
3855 c
2∙108c
1.3∙10 13 c
Transparency No. 1-63
The Foundations
Effect of Speed-ups for different order of functions
Wait for faster hardware!
Consider maximum problem size you can solve in an
hour.
present 100 times faster
1000 times faster
n
N1
100 N1
1000 N1
n2
N2
10N2
31.6 N2
n3
N3
4.64 N3
10 N3
n5
N4
2.5 N4
3.98 N4
2n
N5
N5+6.64
N5+9.97
3n
N6
N6+4.19
N6+2.29
Transparency No. 1-64
The Foundations
Asymptotic notations
Q((g(n)) = {f(n) | $c2,c1 and n0 > 0 s.t. c2g(n)
f(n) c1 g(n) for all n n0 }
O((g(n)) = {f(n) | $ c and n0 > 0 s.t. f(n) cg(n)
for all n n0 }
W((g(n)) = {f(n) | $c and n0 > 0 s.t. c g(n) f(n)
for all n n0 }
o((g(n)) = {f(n) | "arbitrary small c >0 $ n0 > 0
s.t. f(n) < c g(n) for all n n0 }
w((g(n)) = {f(n) | "arbitrary large c >0 $ n0 > 0
s.t. c g(n) < f(n) for all n n0 }
Transparency No. 1-65
The Foundations
Using the asymptotic notations
We use f(n) = D(g(n)) to mean f(n) D(g(n)),
where D = Q,O,o,W,or w.
analog:
O (asymptotic upper bound):
f(n) = O(g(n)) means like f(n) g(n)
o (asymptotic upper bound but not tight): <
f(n) = o(g(n)) means like f(n) < g(n)
W (asymptotic lower bound):
f(n) = W(g(n)) means like f(n) g(n)
w (asymptotic lower bound but not tight): >
f(n) = w(g(n)) means like f(n) > g(n)
Q (asymptotic tight bound : =
f(n) = O(g(n)) means like f(n) = g(n)
Transparency No. 1-66
The Foundations
Exercises
Let f and g be positive real function. Show
that
1. f = O(g) iff g = W(f)
2. f =o(g) iff g = w(f)
3. f =o(g) iff f =O(g) but not f = Q(g)
4 f = w (g) iff f =W(g) but not f = Q(g)
5 f = o(g)
iff
limit n f/g = 0 iff
limit n g/f = iff
g = w(f).
Transparency No. 1-67