* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 20.2 INDUCED EMF
Survey
Document related concepts
Buck converter wikipedia , lookup
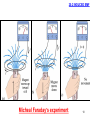
Wireless power transfer wikipedia , lookup
Loading coil wikipedia , lookup
Transformer wikipedia , lookup
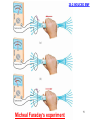
Brushed DC electric motor wikipedia , lookup
Induction motor wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Alternating current wikipedia , lookup
Electric machine wikipedia , lookup
Ignition system wikipedia , lookup
Skin effect wikipedia , lookup
Transcript
UNIT 20 : ELECTROMAGNETIC INDUCTION Electromagnetic induction is the production of an electrical potential difference (induced emf) across a conductor situated in a changing magnetic field. 20.1 20.2 20.3 20.4 20.5 Magnetic flux Induced emf Self-inductance Mutual inductance Energy stored in inductor 1 20.1 MAGNETIC FLUX ,Φ • is defined as the scalar product between the magnetic flux density, B and the vector of the surface area, A. Unit:T.m2 or Wb B A BA cos θ area, A A B B = 90 =0 A BA = 0 2 Example 20.1.1 A small surface of area 10 mm2 inside a uniform magnetic field of strength 0.10 T is inclined at an angle α to the direction of the field. Determine the magnetic flux through the surface if i) α = 0º, ii) α = 30º iii) α = 90º Solution : B A BA cos θ 20.2 INDUCED EMF • An electric current produces a magnetic field. (chapter 19) If electric currents produce a magnetic field, is it possible that a magnetic field can produce an electric current ? • Scientists (American Joseph Henry and the Englishman Michael Faraday) independently found that is possible. • Henry actually made the discovery first, but Faraday published his results earlier and 4 investigated the subject in more detail. 20.2 INDUCED EMF • The diagram below shows the apparatus used by Faraday in his attempt to produce an electric current from a magnetic field. Faraday’s experiment to induce an emf 5 20.2 INDUCED EMF • In this experiment, Faraday hoped by using a strong enough battery, a steady current in X would produce a current in a second coil Y but failed. • Faraday saw the galvanometer in circuit Y deflect strongly at the moment he closed the switch in circuit X. • And the galvanometer deflected strongly in the opposite direction when he opened the switch. • A steady current in X had produced no current in Y. 6 20.2 INDUCED EMF • Only when the current in X was starting or stopping was a current produced in Y. • Faraday concluded that although a steady magnetic field produces no current, a changing magnetic field can produce an electric current. • Such a current is called an induced current. • We therefore say that an induced current is produced by a changing magnetic field. • The corresponding emf required to cause this current is called an induced emf. 7 20.2 INDUCED EMF • Induced emf is an electromotive force resulting from the motion of a conductor through a magnetic field , or from a change in the magnetic flux that threads a conductor. • Faraday did further experiments on electromagnetic induction, as this phenomenon is called.( refer diagram ) a) A current is induced when a magnet is moved toward a coil/loop. b) The induced current is opposite when the magnet is moved away from the coil/loop. c) No current is induced if the magnet does not move relative to the coil/loop. 8 9 20.2 INDUCED EMF Micheal Faraday’s experiment 10 20.2 INDUCED EMF Micheal Faraday’s experiment 11 20.2 INDUCED EMF • Direction of the induced current depends on : i ) the direction of the magnet’s motion and ii) the direction of the magnetic field. • Magnitude of the induced current depends on : i ) the speed of motion (v ↑,Iind↑) ii) the number of turns of the coil (N ↑, Iind↑) iii)the strength of the magnetic field (B↑,Iind↑) • From the observations, Michael Faraday found that, “ the current/emf is induced in a coil/loop or complete circuit whenever there is a change in the magnetic flux 12 through the area surrounded by the coil” Faraday’s law and Lenz’s law 20.2 INDUCED EMF Faraday’s law “the magnitude of the induced e.m.f. is proportional to the rate of change of the magnetic flux” Lenz’s law “an induced electric current always flows in such a direction that it opposes the change producing it.” 13 Faraday’s law and Lenz’s law 20.2 INDUCED EMF • These two laws are summed up in the relationship, dΦB dΦB or dt dt dt : change of time : induced e.m.f. dΦB : change of magnetic flux The (-) sign indicates that the direction of induced e.m.f. always opposes the change of magnetic flux producing it (Lenz’s law). 14 Faraday’s law and Lenz’s law 20.2 INDUCED EMF • The concept of Faraday's Law is that any change in the magnetic environment of a coil of wire will cause a voltage (emf) to be "induced" in the coil. • No matter how the change is produced, the voltage will be generated. • The change could be produced by a) changing the magnetic field strength, b) moving a magnet toward or away from the coil, c) moving the coil into or out of the magnetic field, d) rotating the coil relative to the magnet, etc. 15 (A) Induced emf in coil 20.2 INDUCED EMF Faraday’s law and Lenz’s law 16 (A) Induced emf in coil 20.2 INDUCED EMF Faraday’s law and Lenz’s law dΦB Notes i ) the magnitude of induced emf, dt d dt d or N dt N final initial t final tinitial dB NA dt dA NB dt ii) the flux through the coil can change in any of 3 ways, a) B , b) A , c) θ = B • A = BA cos θ 17 (A) Induced emf in coil 20.2 INDUCED EMF Faraday’s law and Lenz’s law Notes iii) If the coil is connected in series to a resistor of resistance R and the induced e.m.f exist in the coil as shown in figure below. dΦ | | B dt and - I induced R + I induced IR I induced R 18 Lenz's Law (based on censervation of energy) • When an emf is generated by a change in magnetic flux according to Faraday's Law, the polarity of the induced emf (next slide) is such that it produces a current whose magnetic field opposes the change which produces it. • The induced magnetic field inside any loop of wire always acts to keep the magnetic flux in the loop constant. • In the examples below, if the B field is increasing, the induced field acts in opposition to it. • If it is decreasing, the induced field acts in the 19 direction of the applied field to try to keep it constant. (A) Induced emf in coil Faraday’s law and Lenz’s law 7.2 INDUCED EMF The polarity of the induced emf Induced current is directed out of the positive terminal, through the attached device (resistance) and into the negative terminal. 20 (A) Induced emf in coil Faraday’s law and Lenz’s law Example 20.2.1 A coil of wire 8 cm in diameter has 50 turns and is placed in a B field of 1.8 T. If the B field is reduced to 0.6 T in 0.002 s , calculate the induced emf. 21 Faraday’s law and Lenz’s law Solution d = 8 cm, N = 50 turns, B from 1.8 T to 0.6 T in 0.002 s dB NA dt final initial dΦB N N dt t BA final BA initial B final Binitial NA N t t d 2 B final Binitial 151 V N t 2 22 (A) Induced emf in coil Faraday’s law and Lenz’s law Example 20.2.2 An elastic circular loop in the plane of the paper lies in a 0.75 T magnetic field pointing into the paper. If the loop’s diamater changes from 20.0 cm to 6.0 cm in 0.50 s, a)What is the direction of the induced current, b)What is the magnitude of the average induced emf, and c)If the loop’s resistance is 2.5 Ω, what is the average induced current during the 0.50 s ? 23 Faraday’s law and Lenz’s law Solution: B=0.75 T, di= 20.0 cm, df= 6.0 cm, t = 0.50 s a) Direction of the induced current, b) Magnitude of the average induced emf, dA NB dt c) R = 2.5 Ω, 24 Example 20.2.3 Faraday’s law and Lenz’s law A circular shaped coil 3.05 cm in radius, containing 40 turns and have a resistance of 3.55 is placed perpendicular to a magnetic field of flux density of 1.25 x 10-2 T. If the magnetic flux density is increased to 0.450 T in time of 0.250 s, calculate the induced current flows in the coil. 25 (A) Induced emf in coil Faraday’s law and Lenz’s law How to determine the direction of induced current.- Lenz’s law Case A Thumb – induced magnetic field Fingers - induced current N + I induced Direction of induced current – induced-current right hand rule. - I induced 26 Faraday’s law and Lenz’s law How to determine the direction of induced current.- Lenz’s law Case A • Consider a bar magnet that is moved towards a solenoid. • As the north pole of the magnet approaches the solenoid, the amount of magnetic field passing through the solenoid increases , thus increasing the magnetic flux through the solenoid. • The increasing flux induces an emf (current) in the solenoid and galvanometer indicates that a current is flowing. 27 Faraday’s law and Lenz’s law How to determine the direction of induced current.- Lenz’s law Case A • The direction of the induced current is such as to generate a magnetic field in the direction that opposes the change in the magnetic flux, so the direction of the induced field must be in the direction that make the solenoid right end becomes a north pole. • This opposes the motion of the bar magnet and obey the Lenz’s law. 28 Faraday’s law and Lenz’s law How to determine the direction of induced current.- Lenz’s law Case B (a) When the magnet is moved toward the stationary conducting loop, a current is induced in the direction shown. (b) This induced current produces its own magnetic field (Binduced) directed to the left that counteracts the increasing external flux. Bexternal Binduced 29 Faraday’s law and Lenz’s law How to determine the direction of induced current.- Lenz’s law Case B (c) When the magnet is moved away from the stationary conducting loop, a current is induced in the direction shown. (d) This induced current produces a magnetic field (Binduced) directed to the right and so counteracts the decreasing external flux. Bexternal Binduced 30 (A) Induced emf in coil Faraday’s law and Lenz’s law Faraday’s law and Lenz’s law Example 20.2.4 Calculate the current through a 37 Ω resistor connected to a single turn circular loop 10 cm in diameter, assuming that the magnetic field through the loop is increasing at a rate of 0.050 T/s. State the direction of the current. 31 Example 20.2.4 R = 37 Ω , d = 10 cm dB/dt = 0.050 T/s. Faraday’s law and Lenz’s law S N 2 dB d dB | | A dt 2 dt I induced I induced 3.93 x 10-4 I 1.06 x 10-5 A R 37 Direction of Iinduced : from b to a. 32 (B) Induced emf of a straight conductor • Consider a straight conductor of length l is moved at a speed v to the right on a U-shaped conductor in a uniform magnetic field B that points out the paper. dA dx vdt • This conductor travels a distance dx =vdt in a time dt. 33 (B) Induced emf of a straight conductor • The area of the loop increases by an amount dA ldx dA lvdt • According to Faraday’s law, the e.m.f. is induced in the conductor and its magnitude is given by dA dx vdt 34 (B) Induced emf of a straight conductor d dA B dt dt lvdt B dt Blv Blv sin θ = angle between v and B = 90 o ε L vB • This induced emf is called motional induced emf. 35 (B) Induced emf of a straight conductor • As the conductor is moved to the right (Fapplied to the right) with speed v, the magnetic flux through the loop increases. • A current is induced in the loop. • The induced current flows in the direction that tends to oppose this change. FB Fapplied dA dx vdt • In order to oppose this change, the current through the conductor must produce a magnetic force (F=BIL) directed to the left. 36 (B)Induced emf of a straight conductor Faraday’s law and Lenz’s law •The direction of the induced current due to induced e.m.f. flows in the linear conductor can be determine by using Fleming’s right hand rule (based on lenz’s law). • The induced current flows from P to Q. (motion) B Fapplied P FB Q I induced or induced Only for the straight conductor. Fapplied dA dx vdt Thumb – direction of Motion First finger – direction of Field Second finger – direction of Induced current 37 or Induced e.m.f. (B)Induced emf of a straight conductor Polarity • When the conductor is moved to the right (Fapplied to the right) with speed v, the electrons in the rod move with the same speed. • Therefore, each feels a force F=Bqv, which acts upward in the figure. dA dx vdt • If the rod were not in contact with the U-shaped conductor, electrons would collect at the upper end of the rod, leaving the lower end positive. There 38 must thus be an induced emf. Induced emf of a straight conductor Example 20.2.5 Suppose the length in figure above is 0.10 m, the velocity z is 2.5 m/s, the total resistance of the loop is 0.030 Ω and B is 0.60 T. Calculate a) the induced emf b) the induced current c) the force acting on the rod d) the power dissipated in the loop a) | | Blv b) I R c) F BIL d) Pdissipated I 2 R 39 Induced emf of a straight conductor Example 20.2.6 A 0.2-m length of wire moves at a constant velocity of 4 m/s in a direction that is 40 o with respect to a magnetic flux density of 0.5 T. Calculate the induced emf. Blv sin 40 Induced emf of a straight conductor Example 20.2.7 In figure above, a rod with length l = 0.400 m moves in a magnetic flux with magnitude B = 1.20 T. The emf induced in the moving rod is 3.60 V. a) Calculate the speed of the rod. b) If the total resistance is 0.900 Ω, calculate the induced current. c) What force does the field exert on the rod as a result of this current? 7.50 m/s , 4.00 A , 1.92 N to the left 41 42 Fig 31-CO, p.967 (C) Induced emf in a rotating coil An ac generator / dynamo (transforms mechanical energy into electric energy) 43 (C) Induced emf in a rotating coil An ac generator / dynamo (transforms mechanical energy into electric energy) 44 (C) Induced emf in a rotating coil • Consider a coil of N turns each of area A and is being rotated about a horizontal axis in its own plane at right angle to a uniform magnetic field of flux density B. • As the coil rotates with the angular speed ω, the orientation of the loop changes with time. A 45 (C) Induced emf in a rotating coil • The emf induced in the loop is given by Faraday’s law, d N , AB cos AB cos t dt d AB cos t N , A and B are constant dt NAB sin t NAB sin t ε NABω sin θ o sin t , o max NAB • The emf induced in the loop varies sinusoidally in time. 46 (C) Induced emf in a rotating coil 0 0 0 0 0 max max max max A The alternating emf induced in the loop plotted 47 as a function of time. Induced emf in a rotating coil Example 20.2.8 The armature of a simple ac generator consists of 100 turns of wire, each having an area of 0.2 m2 . The armature is turned with a frequency of 60 rev/s in a constant magnetic field of flux density 10-3 T. Calculate the maximum emf generated. max NAB 48 Induced emf in a rotating coil Example 20.2.9 ε (V) 28 V 0.42 s 0 0.21 s t 0.63 s 0.84 s -28 V The drawing shows a plot of the output emf of a generator as a function of time t. The coil of this device has a cross-sectional area per turn of 0.020 m2 and contains 150 turns. Calculate a)The frequency of the generator in hertz. b)The angular speed in rad/s c) The magnitude of the magnetic field. 2.4 Hz , 15 rad/s , 0.62 T 49 Induced emf in a rotating coil Example 20.2.10 An amarture in ac generator consists of 500 turns, each of area 60 cm2 . The amarture is rotated at a frequency of 3600 rpm in a uniform 2 mT magnetic field. Calculate a) the frequency of the alternating emf b) the maximum emf generated c) the instantaneous emf at time when the plane of the coil makes an angle of 60o with the magnetic field ? 380 rad/s, 1.13 V, 2.26 V 50 20.3 SELF-INDUCTANCE • Self-induction is defined as the process of producing an induced e.m.f. in the coil due to a change of current flowing through the same coil. S N I S R I • Consider a current is present in the circuit above. 51 20.3 SELF-INDUCTANCE • This current produces a magnet field in the coil that causes a magnetic flux through the same coil. • This flux changes when the current changes. • An emf is induced in this coil called a selfinduced emf. S N I S R • This coil is said to have self-inductance (inductance). • A coil that has inductance is called an inductor. I 52 20.3 SELF-INDUCTANCE • The symbol for an inductor is if air-cored, and a core of magnetic material. if it has • By Lenz’s law, the induced current opposes the change that cause it. • If the current is increasing, the direction of the induced field and emf are opposite to that of the current, to try to decrease the current. • If the current is decreasing, the direction of the induced field and emf are in the same direction as the current, to try to increase the 53 current. 20.3 SELF-INDUCTANCE Iinduced Iinduced (a) A current in the coil produces a magnetic field directed to the left. (b) If the current increases, the increasing magnetic flux creates an induced emf having the polarity shown by the dashed battery. (c) The polarity of the induced emf reverses if 54 the current decreases. 20.3 SELF-INDUCTANCE • The magnetic flux in a coil is proportional to the current ΦB I ΦB LI L : self - inductance of the coil • From the Faraday’s law, dΦB …. (1) ε dt dI L dt d LI ε dt …. (2) 55 dI L dt L dI 20.3 SELF-INDUCTANCE dt Self-inductance, L is defined as the ratio of the self induced e.m.f. to the rate of change of current in the coil. 56 (1) = (2) 20.3 SELF-INDUCTANCE dΦB dI L dt dt If the coil has N turns, hence dI dΦB L N dt dt L dI N dΦB LI NΦB NΦB L I - scalar quantity - unit is henry (H). 1 H 1 Wb A-1 1 T m 2 A-1 57 20.3 SELF-INDUCTANCE NΦB L I • The value of the self-inductance depends on a) the size and shape of the coil b) the number of turn (N) c) the permeability of the medium in the coil (). • Self-inductance does not depend on current. 58 20.3 SELF-INDUCTANCE Self-inductance of a Loop and Solenoid NΦB μ NI 0 From L And B ΦB BA cos 0 I l By substituting we get, μ0 N 2 A 2 L μ n Al or L 0 l N n l For the medium-core solenoid : μr μ0 N 2 A μN 2 A or L L l l where μr : relative permeabili ty μ : permeabili ty of medium A : area of the solenoid μ μr μ0 59 20.3 SELF-INDUCTANCE Example 20.3.1 If the current in a 230 mH coil changes steadily from 20.0 mA to 28.0 mA in 140 ms, what is the induced emf ? dI L dt (Given 0 = 4 x 10-7 H m-1) Example 20.3.2 μN L Suppose you wish to make a solenoid l whose self-inductance is 1.4 mH. The inductor is to have a cross-sectional area of 1.2 x 10 -3 m2 and a length of 0.052 m. How 60 many turns of wire needed ? 220 turns 0 2 A 20.3 SELF-INDUCTANCE Example 20.3.3 The current in a coil of wire is initially zero but increases at a constant rate; after 10.0 s it is 50.0 A. The changing current induces an emf of 45.0 V in the coil. a) Calculate the self – inductance of the coil. b) Calculate the total magnetic flux through the coil when the current is 50.0 A. a) L dI dt b) NΦB L I 61 20.3 SELF-INDUCTANCE Example 20.3.4 A 40.0 mA current is carried by a uniformly wound air-core solenoid with 450 turns, a 15.0 mm diameter and 12.0 cm length. Calculate a) the magnetic field inside the solenoid. b) the magnetic flux through each turn. c) the inductance of the solenoid. (Given 0 = 4 x 10-7 H m-1) a) B μ0 NI l b) ΦB BA cos 0 c) NΦB L I or μ0 N A L l 2 62 20.4 MUTUAL INDUCTANCE 20.4 MUTUAL INDUCTANCE Mutual Inductance for two coaxial solenoids A N1 N2 I1 l Ac generator I1 • Consider a long solenoid with length l and cross sectional area A is closely wound with N1 turns of wire. A second solenoid with N2 turns surrounds it at its centre as shown in figure above. Mutual Inductance for two coaxial solenoids 20.4 MUTUAL INDUCTANCE • The first solenoid is the one connected to an ac generator, which sends an alternating current I1 through it. • The current I1 produces a magnetic field lines inside it and this field lines also pass through the solenoid 2 as shown in figure. • If the current I1 changes with time, the magnetic flux through the solenoids 1 and 2 will change with time simultaneously. • Due to the change of magnetic flux through the solenoid 2, an e.m.f. is induced in solenoid 2. • This process is known as mutual induction. • At the same time, the self-induction occurs in the 64 solenoid 1 since the magnetic flux through it changes. Mutual Inductance for two coaxial solenoids 20.4 MUTUAL INDUCTANCE • Mutual induction is defined as the process of producing an induced e.m.f.in one circuit/coil due to the change of current in another circuit/coil. Mutual inductance, M • If the current I1 in solenoid 1 is continously changing, then the flux it produces will also change continously. • The changing magnetic flux from the solenoid 1 induces an emf in the solenoid 2. • The induced emf in the solenoid 2 is proportional to the rate of change of the current I1 in solenoid 1. dI 1 2 dt dI1 ….. (1) 2 M 21 dt 65 Mutual Inductance for two coaxial solenoids Mutual inductance, M 20.4 MUTUAL INDUCTANCE • Also the induced emf in the solenoid 1 is proportional to the rate of change of the current I2 in solenoid 2. dI 2 1 dt dI 2 1 M 12 dt M 21 M12 M a constant of proportionality mutual inductance • The mutual inductance of the two solenoids is the same if current flows in the solenoid 2 and flux links the solenoid 1, causing an induced emf when a change in flux linkage occurs. 66 Mutual Inductance for two coaxial solenoids Mutual inductance, M • Rearrange, M 2 dI1 dt 20.4 MUTUAL INDUCTANCE 1 dI 2 dt M is defined as “ the ratio of the induced emf in one solenoid/coil/ to the rate of change of current in the other solenoid/coil.” • Unit M : Henry (H) • From Faraday’s law, d N dt d2 2 N2 dt ….. (2) 67 Mutual Inductance for two coaxial solenoids Mutual inductance, M (1) = (2) 20.4 MUTUAL INDUCTANCE dI1 d2 M 21 N2 dt dt M 21 dI1 N 2 dΦ2 M 21I1 N 2Φ2 N 2Φ2 M 21 I1 • Since M12=M21=M, equation above can be written as N 2Φ2 N 1Φ1 M I1 I2 68 Mutual Inductance for two coaxial solenoids Mutual inductance, M • From N 2Φ2 M 21 I1 20.4 MUTUAL INDUCTANCE and 2 B1 A o N1 I 1 A l • He mutual inductance of the solenoid 2 is, N 2Φ2 N 2 o N1 I1 A M 21 I1 I1l M 21 M 12 M N 2Φ2 N 1Φ1 M I1 I2 o N 2 N1 A l M o N 2 N1 A l 69 20.4 MUTUAL INDUCTANCE Mutual inductance, M N 2Φ2 N 1Φ1 M I1 I2 M o N 2 N1 A l dI 2 1 M 12 dt 70 20.4 MUTUAL INDUCTANCE Example 20.5.1 The primary coil of a solenoid of radius 2.0 cm has 500 turns and length of 24 cm. If the secondary coil with 80 turns surrounds the primary coil at its centre, calculate a. the mutual inductance of the coils b. the magnitude of induced e.m.f. in secondary coil if the current in primary coil changes at the rate 4.8 A s-1. 71 7.5 MUTUAL INDUCTANCE Solution 20.5.1 rp = 2.0 cm , Np =500 , lp 24 cm Ns = 80 dIs/dt = 4.8 A s-1 a) M M o N 2 N1 A l o N s N p A lp dI 2 b) 1 M 12 dt s M dI p dt 72 73 20.4 MUTUAL INDUCTANCE Transformer Vp (input) primary coil NP turns laminated iron core NS turns Vs (output) secondary coil Symbol in circuit • A transformer is a device for increasing or decreasing an ac voltage. • The operation of transformer is based on the 74 principle of mutual induction and self-induction. Transformer 20.4 MUTUAL INDUCTANCE • Two types of transformer a) step-up transformer (Ns > Np) b) step-down transformer (Np > Ns). • There are three assential parts; (1) a primary coil connected to an ac source (2) secondary coil (3) soft iron core • When ac voltage is applied to the input coil (primary coil), the alternating current produces an alternating magnetic flux that is concentrated in the iron core, without any leakage of flux outside the core. 75 20.5 ENERGY STORED IN INDUCTOR • The functions of an inductor are ; - to control current - to keep energy in the form of magnetic field • An inductor carrying current has energy stored in it. • It is because a generator does work to establish a current in an inductor. • Suppose an inductor is connected to a generator whose terminal voltage can be varied continously from zero to some final value. 76 20.5 ENERGY STORED IN INDUCTOR • As the voltage is increased, the current I in the circuit rises continously from zero to its final value. • While the current is rising, an emf (back emf) is induced in the inductor. • Because of this, the generator that supplies the current must maintain a potential difference between its terminals while the current is rising (changing), and therefore it must supply energy to the inductor. • Thus, the generator must do work to push the charges through the inductor against this induced emf. 77 20.5 ENERGY STORED IN INDUCTOR • To do this, power has to be supplied by the generator to the inductor. W U W P I P t dI dW dU P I L P dt dt dt dU Pdt Pdt LIdI • The total work done while the current is changed from zero to its final value is given by U I 0 0 dU L dI 1 2 U LI 2 • This work is stored as energy in the inductor. 78 20.5 ENERGY STORED IN INDUCTOR • For a long air-core solenoid, the self-inductance is μ0 N 2 A L l • Therefore the energy stored in the solenoid 2 2 is given by U 1 LI 2 μ N AI 1 2 U 2 0 l Example 20.5.1 How much energy is stored in a 0.085-H inductor that carries a current of 2.5 A ? 1 2 U LI 2 79 20.5 ENERGY STORED IN INDUCTOR Example20.5.2 A steady current of 2.5 A in a coil of 500 turns causes a flux of 1.4 x 10-4 Wb to link (pass through) the loops of the coil. Calculate a) the average back emf induced in the coil if the current is stopped in 0.08 s b) the inductance of the coil and the energy stored in the coil (inductor). dΦB | | dt dI L dt 1 2 U LI 2 80