Download Photonic Devices and Systems (ELEC ENG 4EM4)

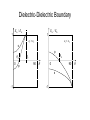
Basics of Optics
-Maxwell’s equations
-From Maxwell’s equations to the wave
equation
- Plane wave as the free-space solution to the
wave equation
- Plane wave at the boundary: reflection and
refraction
- Wave confinement and waveguide
Maxwell’s Equations
• Coulomb’s law：

F
e1e2 
er
40 r122
1
E
F
1 e1
1 Ze

e

er
r
e2 4 0 r122
4 0 r 2
• Feature 1: why inverse square law?
Maxwell’s Equations
• Total force flux must be conserved in 3D space and
equal to the source (i.e., total “detected” = total “created”)
• We immediately have Gaussian law:
 
Ze
E

d
s

s
40
1   Ze
1
e

d
s


s r 2 r
0
0

V
dV


E 
0
• Coulomb force in spaces with other dimensions
Maxwell’s Equations
• Feature 2: centric force
• We therefore know that the static electric field is curl-free:

rB
rA
  Ze rB 1   Ze rB 1
Ze rB 1
Ze 1 1
E  dl 
e

d
l

dr

dr

(  )
r
40 rA r 2
40 rA r 2
40 rA r 2
40 rA rB
 
 E  dl  0

 E  0
l
• From Helmholtz’s law, a vector is uniquely specified by
its divergence and curl, hence Gaussian law plus curlfree description is equivalent to Coulomb’s law
• Why go from the direct (explicit) description to constraint
(implicit) description?
Maxwell’s Equations
• Constraint description
– Field is specified in a limited set of spatial points, not specified in
the rest area (– not specified doesn’t necessarily mean that the
field is zero)
– Specification is given in the form of equations – implicit
expressions
– These equations must be in the differential or integral form,
cannot be in simple algebraic form
• Why constraint description
– We have to deal the coupling between the electric and magnetic
field later – it is easier to deal with coupling problems if we
express source by field, rather than to express field by source.
Maxwell’s Equations
• Current definition:


dr

J  v  
dt
• Total charge must be conserved, the net current flow
through a closed surface must be equal to the change of
charge density enclosed by the surface, hence we have
the charge conservation law:
 
 ( Ze)

J

d
s




dV
s

V
t
t


J  
t
Maxwell’s Equations
• Another constant current flow will feel the Biot-Savert force, hence we
have Biot-Savert’s law:
 0
F
4

l1 l2

 
I1dl1  ( I 2 dl2  er )
r122

   0 I 2 dl 2  er  0

  B(r ) 
2

l2
4

4
r
I 1dl1 
12

F

l1
' 
Idl  er r '
l ' | r  r ' |2
• Biot-Savert force is similar to Coulomb’s force, only the interactive scalar
charges are replaced by the interactive unit current flow vectors
• Coulomb’s force is originated by the point sources (and their
superposition), whereas Biot-Savert’s force comes from the vortex
sources (and their superposition) – a vortex cannot be reduced to a
single point, and exists only in space with dimension higher than 3!
• Biot-Savert’s force only acts on current flows, has no effect on static
charges, hence is an independent force (cannot be included by
Coulomb’s force)
Maxwell’s Equations
• Feature 1: close vector flow
• Magnetic field is continuous in 3D space →
divergence free
• Vector potential can be introduced, and we have
Gaussian law for magnetic field:
 

B(r )  0
4

l'
' 
Idl  er r '
0

 
4
| r  r ' |2


B   A
 
J  er r '
0
dV
'



V | r  r ' |2
4

B  0

J
V | r  r ' |dV '
Maxwell’s Equations
• Feature 2: non-centric field anymore, otherwise,
divergence free plus curl free makes no magnetic field
anywhere (following Helmholtz’s theorem); and the
magnetic force, again, follows the inverse square law as
a function of the interactive distance
• Reason – magnetic flux must be conserved in 3D space
• Also from which, we can derive Ampere’s law:





2
  B      A  (  A)   A  0   2 0
4


J
V | r  r ' |dV '   0 J
Maxwell’s Equations
• Electric field interacts between two static charges, reflects
a pure “adiabatic” effect
• Magnetic field interacts between two moving charges,
reflects a pure “derivative” effect
• Electric + Magnetic field provides a complete description
Maxwell’s Equations
• Static charge distribution creates a curl free, divergence
driven field; the field can be detected by another charge,
hence “electric” field
• Constant current flow not only creates an electric field, it
also creates a divergence free, curl driven field; the field
can be detected by another current, enhance “magnetic”
field
• Up to now, the electric and magnetic field are static,
without any coupling in between
Maxwell’s Equations
Static Electric Field
Field Explicit
Description
Field Implicit
Description
E (r ) 
1
4 0
Static Magnetic Field
 (r ')eˆrr '
 | r  r ' |
2
V'
 
  E (r ) 

 (r )
0
 
  E (r )  0
B(r ) 
dV '

0
4
0
4

V'

L'
Idl ' eˆrr '
| r  r ' |2
J (r ')  eˆrr '
dV '
| r  r ' |2
 
  B(r )  0
 

  B(r )   0 J
Maxwell’s Equations
• However, there is no absolute inertia system – moving or
steady depends on the system where the observer stays,
hence a static charge and a constant current can be
exchanged
• Therefore, the static electric field comes from a static charge
and the static magnetic field comes from a constant current
can be exchanged!
• How can we have a consistent description then?
Maxwell’s Equations
• Unify the static electric and magnetic fields as a single 3D
vector in a unified spatial - temporal 4D space, under the
non-relativistic condition, we have:
E' EvB
B'  B 
v
E
2
c
to make the E/M description consistent
Maxwell’s Equations
• Accelerated electron creates time-varying current, timevarying current creates time-varying magnetic field, timevarying magnetic field will create electric field vortex
• Why?
• Explanation – isolated natural system tend to eliminate
any disturbance, with time evolution towards its eigen
state: once a time-varying magnetic field is established, a
electric field vortex will be induced, to establish yet
another magnetic field with an opposite change towards a
cancellation of the total field, hence Faraday’s law holds

t
 
 
 B  ds   E  dl  0
s
l


B
 E  
t
Maxwell’s Equations
• Accelerated charge causes a time-varying charge distribution,
leading to a time-varying current; from Ampere’s law, time-varying
magnetic field exists; from Faraday’s law, electric vortex exists
• Therefore, not only electric field can be generated in its divergence
form by the static charge distribution, it can also be generated in its
curl form by the “temporary” charge distribution which
• Indicating that the electric field is brought in by both its divergence
and curl, following the Helmholtz theorem, the electric field is
complete
• Hence, time-varied magnetic field excites electric field, electric and
magnetic fields become coupled; however, such coupling is still unidirectional
Maxwell’s Equations
Static
charge
Div.
Time-varying charge
distribution (time-varying
current, temporary charge)
Moving charge, static charge
distribution (constant current)
Div.
Curl
Curl
Static Electric
Field
Time-varying
electric field
Static Magnetic
Field
Time-varying
magnetic field
Curl


J  
t
Charge conservation law
Gauss’s law
 
E 
0

B  0
Ampere’s law
  B  0 J
Faraday’s law


B
 E  
t
(Derived from Coulomb’s law)
(Derived from Biot-Savert’s law)
Maxwell’s Equations
• Contradiction between Ampere’s law and the charge
conservation law


    B  0  J

0


 0

t
• Maxwell mended Ampere’s law, solved the problem


 


E
    B   0 (  J 
)
  B   0 J   0 0
t
t


 
Gaussian law is called   E 
0

0
0
Maxwell’s Equations
• Significance – likes a current, the time-varying electric field can
generate magnetic field
• Hence the time-varying rate of the electric displacement vector is
equivalent to a current, named as the displacement current; the
conventional current caused by the moving charge is then called
the conduction current to make a difference
• Not only time-varying magnetic field, equivalent to temporary
charges, can excite electric field, time-varying electric field,
equivalent to a “temporary” current (i.e., the displacement current),
can also excite magnetic field
• Finally, electric and magnetic fields are fully coupled through mutual
excitation
Maxwell’s Equations
• Therefore
– 1. accelerated charge creates time-varying magnetic field in its
neighborhood (through the time-varying conduction current and
following Ampere’s law);
– 2. time-varying magnetic field excites electric field in its
neighborhood (through Faraday’s law)
– 3. time-varying electric field excites magnetic field in its
neighborhood (through Ampere’s law)
• Step 2 and 3 form a sustainable loop, and make electricmagnetic fields propagation! Such an electric-magnetic
non-local oscillation is named as the electromagnetic
wave
Maxwell’s Equations in Vacuum


Faraday’s law
B
 E  
t

Maxwell modified Ampere’s law,


E
  B   0 J   0 0
derived from Biot-Savert’s law
t

  E   / 0
Gaussian law, derived from Coulomb’s law

B 0
Gaussian law, derived from Biot-Savert’s law
Maxwell’s Equations in General Form


B
 E  
t


 D
 H  J 
t

D  

B  0


D  E


B  H


J  E
17 equations, yet 16 unknowns, one equation is redundant,
e.g., the 4th equation is embedded in the 1st equation
Why independent sources, i.e., the free charge and conduction
current, have to be taken as unknowns as well?
Wave Equation
• From Maxwell’s equations to the wave equation
sourceless, harmonic

B
t

 H  J 
D
t
 E  
homogeneous medium
 E  j B  j H
    E   2 E
 H   j D   j E
   H   2 H
(  E )   2 E   2 E
coupling term
independent term
Wave in Free Space
• Simplified wave equation
sourceless, homogenous
 D    0    E    E   E   E  0   E  0
simplified wave equation
 2 E   2 E  0
from
B  0   H  0
we have 2 H   2 H  0
• Obviously, to manipulate the polarization through coupling
among different field components, the introduction of
medium inhomogeneity and/or structure is necessary
• Free space solution of the wave equation – plane harmonic
wave 
 
E0 e j ( k r t )
 j ( kr t )
H 0e
where
 2
| k |   2  or
| k |  
The Wave Concept
• Solution to wave equation – traveling wave
– 1D f ( z  vt ) or f (  z  t ) propagation along 
– 3D f (k  r  t ) propagation along k
t
z
• The element of traveling wave and its complex expression
– plane harmonic wave
sin(k  r  t ), cos(k  r  t )  e j ( k r t )
The Wave Concept
• Standing wave – formed by the superposition of two contradirectionally propagating (traveling) waves
cos(k  r ) cos(t )  cos(k  r )e jt
• Evanescent wave – spatially decayed wave
e ki r cos(kr  r  t )  e ki r e j ( kr r t )
• Wave coupling – phase matching condition
cos(k1  r  1t ), cos(k2  r  1t )
kˆ11 kˆ22

| k1 |
| k2 |
• Phase velocity and group velocity
vp 
 c
d  d (c | k | / n )
| k | dn
 dn
 , vg 

 v p (1 
)  v p (1 
)
|k| n
d |k|
d |k|
n d |k|
n d
Wave in Free Space

• Dispersion in free space
1/ 
1/ 
|k |
• Plane harmonic wave characteristics
 E  0   [ E0e j ( k r t ) ]  e j ( k r t )  E0  ( jk  E0 )e j ( k r t )  0  k  E0  0
for the same reason k  H 0  0
we have k0  E0   /  H0


also from   E  j H   H   jE
k0  H0    /  E0
where
k0  k / | k |
Wave in Free Space
• Therefore, the plane harmonic wave in free space has its
electric field, magnetic field, and propagation direction all
orthogonal – it is a condition forced by the electric and
magnetic divergence free requirement


| E0 |  /  | H 0 |
E [V/m]
k
free space impedance
H [A/m]
Wave in Free Space
• Significance of the plane harmonic wave – eigen solution of
the wave equation in free space, i.e., for whatever
excitation, after waiting for infinitely long, the solution at
infinitely far distance from the source in free space can only
be the plane harmonic wave
• Therefore, regardless of the source distribution, the
electromagnetic wave in free space will become the plane
harmonic wave after infinitely long at infinity, the evolution
process is the spatial diffraction that eventually smears out
any initial nonuniformity
Plane Harmonic Wave at Boundary
z
ki
i r
[ E0i e j ( ki r t )  E0 r e j ( kr r t ) ]t  [ E0t e j ( kt r t ) ]t
kr
z=0
t
kt
must hold for any point (x, y) at plane z=0, hence
ki  r |z 0  kr  r |z 0  kt  r |z 0
or
kix  krx  ktx , kiy  k ry  kty the three wave vectors have identical projection
on the boundary plane
Feature 1：The incident wave vector can always be selected in a plane (y=0)
perpendicular to the boundary plane (z=0). As such, the reflected and
refracted wave vectors must be in the same plane (y=0), since kiy=0 requires
kry= kty=0 as well. This plane (y=0) is called the incident plane.
Feature 2: ki sin i  kr sin r  kt sin t or  11 sin i   11 sin r    2 2 sin t
i.e., i  r , 11 sin i   2 2 sin t Snell’s law
Plane Harmonic Wave at Boundary
z
E-field parallel to the boundary (s-wave):
i r
ki
E0i  E0 r  E0t
kr
z=0
t
or
kt
E
H
Hence
E0 r

E0i
H 0i cos i  H 0 r cos  r  H 0t cos t
1
cos i 
1
1
cos i 
1
E0i  E0 r  E0t
1


E0i cos i  1 E0 r cos r  2 E0t cos t
1
1
2
2
cos t
2
2
cos t
2
1
cos i
1
E0t

E0i
1

cos i  2 cos t
1
2
2
Plane Harmonic Wave at Boundary
H-field parallel to the boundary (p-wave):
z
i r
ki
z=0
t
H
Hence
H 0i  H 0 r  H 0t
kr
kt
E0i cos i  E0 r cos  r  E0t cos t
or
H 0i  H 0 r  H 0t
1
1
2
H 0i cos i 
H 0 r cos  r 
H 0t cos t
1
1
2
E
H 0r

H 0i
1
cos i 
1
1
cos i 
1
2
1
cos t
cos i 
2
1
E0 r


E0i
2
1
cos t
cos i 
2
1
1
cos i

H 0t
1

H 0i
1
2
cos i 
cos t
1
2
2

E0t

E0i
2
cos t
2
2
cos t
2
2
cos i
2
1
2
cos i 
cos t
1
2
2
Dielectric-Dielectric Boundary
For non-magnetic materials 1  2  0
E0 r

E0i
s-wave
E0t

E0i
E0 r

E0i
1 cos i   2 cos t
k  ktz
 iz
kiz  ktz
1 cos i   2 cos t
2 1 cos  i
1 cos i   2 cos  t

2kiz
kiz  ktz
 2 cos i  1 cos t
k /   ktz /  2
 iz 1
kiz / 1  ktz /  2
 2 cos  i  1 cos  t
p-wave
E0t

E0i
2 1 cos i
 2 cos i  1 cos t

2kiz / 1
1
 2 kiz / 1  ktz /  2
Dielectric-Dielectric Boundary
1
E0 r / E0i
s
B
0
p
1
E0 r / E0i
1   2
1   2
p
C
90

0
90
s
-1
-1
B

Total Internal Reflection

Under the internal
sin t  1 sin i  sin i
reflection scheme
2
t  i for i  C  sin 1  2
1
2
total reflection happens. Since cos t  1  sin t  1 
1 2

sin i  j | 1 sin 2 i  1|
2
2
is purely imaginary, the refracted wave vector becomes:
ktz    2 0 cos t  j  2 0 |
ktx    2 0 sin t    2 0
1
sin 2  i  1|
2
1
sin  i   10 sin  i  kix
2
i.e., the refracted wave is propagating along the boundary, decaying in the direction
perpendicular to the boundary.
Therefore, the refracted wave under TIR is reduced to a surface wave propagating
along the boundary only, formed by the projection of the incident and reflected
wave vectors on the boundary plane.
TIR as an All-Pass Filter
Once i  C we find
s-wave
p-wave
E0 r kiz  j | ktz |
|k |

 e2 js , s  tan 1 tz  tan 1
E0i kiz  j | ktz |
kiz
2 |
E0 r kiz / 1  j | ktz | / 2
 |k |
2 j

 e p ,  p  tan 1 1 tz  tan 1
E0i kiz / 1  j | ktz | / 2
 2 kiz
1
sin 2 i  1|
2
1 cos i
1 |
1 2
sin i  1|
2
 2 cos i
Applications of TIR
• APF – for polarization splitting and conversion (example:
wave plate)
• Stop the traveling wave – for waveguide
• Under TIR, refracted wave is traveling along the surface –
for surface wave excitation
• TIR is not wavelength sensitive, however, its combination
(multiple TIR) is wavelength sensitive! – for construction of
BPF
Total Refraction
If i  t  90 we have
Hence
1 sin i   2 sin(90  i )   2 cos i or i  tan 1
 2 cos i  1 cos t   2 cos  B  1 sin  B   2 cos  B (1 
2
 B
1
1
tan  B )  0
2
For p-wave, if the incident angle hits the Brewster angle, total refraction happens.
For s-wave, total refraction is impossible, since for 1   2 we always have
1 cosi   2 cost  1  1 sin 2 i   2   2 sin 2 t  1  1 sin 2 i   2  1 sin 2 i  0
Total Reflection and Total Refraction
• Total reflection happens to both s- and p- waves for internal
reflection (when incident light from high refractive index
medium); it doesn’t happen to external reflection (when
incident light from low refractive index medium); hence the
name total internal reflection.
• Total refraction, however, only happens to p-wave,
regardless of internal or external incidence; it doesn’t
happen to s-wave.
• Why total refraction can happen?
• What will happen at the boundary with identical permittivity
but different permeability?
Applications of Total Refraction
• Polarization splitting
• Filtering (Once the medium is dispersive, the Brewster
angle becomes wavelength dependent. Otherwise, a front
stage, e.g., a prism or a diffractional grating, is needed to
convert the wavelength change into the angle change)
Free Space and Plane Wave
• Propagating wave in free-space – for any source,
it will gradually turn itself into a plane wave as it
propagates in free-space, and becomes more
difficult to be collected in a distance away, for a
limited receiver surface
• How can we force the EM wave to propagate
along a specific direction without any spreading
in the 3D world? – That comes to the waveguide
concept
The Concept of Waveguide
• The wave has to localized in certain directions
• How to localize the wave? – Convert the traveling wave
into the standing wave
• Introduce the transverse resonance
kx2
| k2 |   2 

k x1
x
| k2 |    k
2
2
2
x2
| k1 |  1

s-wave reflection at the boundary:
z
| k1 |2   2  k x21
2
1
R
k x1  k x 2
k x1  k x 2
standing wave is formed underneath
the boundary
The Concept of Waveguide
2
d
E0
1
x
E0 R 2 e jk x1 (2 d )
z
The resonance condition for standing
wave in transverse direction (x):
E0  E0 R 2e jkx1 (2 d )  R 2e jk x1 (2 d )  1
A necessary condition is: | R | 1
How to make it possible?
TIR – dielectric waveguide
Conductor reflection – metallic waveguide
Photonic crystal – Bragg waveguide
Plasma reflection – plasmonic polariton waveguide
The Dielectric Waveguide
If k x 2 becomes purely imaginary, or:  2 | k2 |2   2 2   kx 2  | k2 |2  2  j  2   2 2 
k  k x 2 k x1  j | k x 2 |
|k |
R  x1

 e2 j ,   tan 1 x 2  tan 1
k x1  k x 2 k x1  j | k x 2 |
k x1
 2   2 2 
 21   2
The resonance condition becomes: e4 j e2 jk d  1  2k x1d  4  2m
x1
d  1    2 tan
2
2
1
 2   2 2 
 2   2 2 
d
m
2
2
 m  tan(  1   
)
2
2
 21   2
 21   2
Even mode tan  1   
2
2
 2   2 2 
 1  
2
2
Odd mode
Obviously, we have:   2      1
we find:
 r 2  n2  neff  n1   r1
1
tan  21   2
or:
Dispersion relation for the
dielectric slab waveguide

 2   2 2 
 21   2
With definition     0  neff
neff - waveguide effective index
The Dielectric Waveguide

Dispersion relation
E-field E0 ( x )e j ( z t ) (y-component)
Symmetric (even mode):
1/  2   c / n2
1/ neff  0   c / neff
1/ 1  c / n1


Ae  k x 2 ( x  d / 2 ) , x  d / 2

E0 ( x)   B cos( k x1 x),  d / 2  x  d / 2
k x 2 ( x d / 2)

Ce
, x  d / 2

Anti-symmetric (odd mode):

Ae  k x 2 ( x  d / 2 ) , x  d / 2

E0 ( x )   B sin( k x1 x ),  d / 2  x  d / 2
 Ce k x 2 ( x  d / 2 ) , x   d / 2

A, B, C – given by the tangential boundary condition
H-field is given by the Faraday’s law, with x and z
components only – that’s the TE wave
Metallic Waveguide
By letting k x 2  j in previous derivations, we will be able to obtain the
EM wave solution in metallic waveguide.
1D (slab) or 2D dielectric waveguide – support TE and TM waves, not
TEM wave
1D (slab) metallic waveguide – support all TEM, TE, and TM waves
2D (hollow) metallic waveguide – support TE and TM waves, not TEM
wave
Transmission Line – TEM Wave
2
 2  E0 x ( x, y) 
For TEM wave:   k    Hence: ( 2  2 ) 
0
E
(
x
,
y
)
x
y  0 y

TEM solution is the same as the static electric and magnetic field solution.
E
I
I
E
H
parallel lines or
H twisted pair
coaxial cable
TEM Wave - Characteristics
•
TEM wave – “localized” plane wave with k, E, H mutually orthogonal: k is
along the direction in which the waveguide (transmission line) is extended; Eand H- fields are restricted in the 2D cross-section, with their longitudinal
dependence identical to the plane wave, and transverse dependence identical
to the static E- and H- fields with the same boundary condition.
•
Propagation of the TEM wave relies on the free charge and conduction current
on the metal (conductor) – dielectric surface. Namely, the TEM wave is a
resonance between the EM fields and the free charge distribution.
•
For the TEM wave, we can readily introduce the voltage and current concept
to turn a field problem into a circuit problem.
•
The TEM wave can be supported by the dual conductor transmission line:
– Parallel lines or twisted pair
– Coaxial cable
– Printed metal stripe lines (on PCB or other substrates)
•
The TEM wave has no cut-off frequency, it can send DC power through.
Various Waveguides for EM Waves
WG Structure
Guiding
Pattern
Applications
Remarks
DC
Paired metal wires
TEM
Power transmission
Transmission in freespace impossible
VLF
Paired metal wires or
free-space
TEM or plane
wave
Power transmission,
submarine
communication
Huge antenna size
required for broadcasting
LF-MF
Paired metal strips on
PCB or free-space
TEM or plane
wave
Circuits, (AM)
broadcasting
MF for radio
broadcasting
HF-VHF
Coaxial cables, microstrips on PCB, or freespace
TEM or plane
wave
Circuits, (FM)
broadcasting, wireless
communication, remote
control, blue tooth, etc.
TV broadcasting
MW
Coaxial cables, hollow
metallic waveguides, or
free-space
TEM, TE/TM,
HE/EH, or
plane wave
Circuits, radars, space
(satellite) communication
Long-haul
telecommunication
through antenna relay
LW
Optical fibres, dielectric
waveguides, or freespace
TE/TM,
HE/EH, or
plane wave
Optical communication,
sensor systems, space
(satellite) communication
Li-Fi (Lightening LED for
Wi-Fi)