Download By Angles

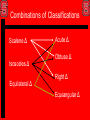
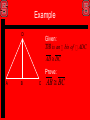
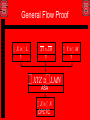
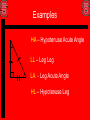
4.1 Classifying Triangles
Classifying Triangles
By Sides
• Scalene Δ
A triangle with no two
sides congruent.
• Isosceles Δ
A triangle with two or
mores sides
congruent.
• Equilateral Δ
A triangle with all sides
congruent.
By Angles
• Acute Δ
A triangle with all acute
angles.
• Obtuse Δ
A triangle with one obtuse
angle.
• Right Δ
A triangle with one right angle.
• EquiangularΔ
A triangle with all angles
congruent.
Combinations of Classifications
Scalene Δ
Isosceles Δ
Equilateral Δ
Acute Δ
Obtuse Δ
Right Δ
Equiangular Δ
What Can You Determine?
• Distance Formula?
• Lengths of segments, thus you can
determine if segments are congruent or not.
• Helps with classification by sides?
• Can it help with classification by angles?
• Pythagorean Theorem…
 If leg2 + leg2 = Hypt2, then it is a Rt Δ
• What can slopes help you with?
• Slopes can help determine if a Rt Δ
4.2 Angles of Triangles
Angle Sum Theorem
• Angle Sum Theorem – The sum of the
measures of the angles of a triangle equals
180°.
A
B
Three adjacent angles –
the sum of their
measurements is 180
C
Third Angle Theorem
• The Third Angle Theorem (No Choice
Theorem) states if two angles in one
triangle are congruent to two angles in
another triangle, then the third set of angles
are also congruent.
90°
60°
90°
30°
60°
30°
Exterior Angles
• Exterior Angle – An angle made between
one side of a triangle and the extension of
the other side.
5
6
1
2
3
4
• There six exterior angles in a triangle,
two per vertex.
Exterior Angle Theorem
• Exterior Angle Theorem – The measure of
the exterior angle of a triangle is equal to
the sum of the two remote interior angles.
C
1
B
2
A
Triangle Sum Theorem
m<2 + m<A + m<C = 180
<1 and <2 are LP,
therefore Supplementary
m<2 + m<1 = 180
Substitution: m<2 + m<1 = m<2 + m<A + m<C
Add/Subt: m<1 = m<A +m<C
Triangle Corollaries
• Corollaries are just like theorems but are
easily proved.
• Two Triangle Corollaries are:
 The acute angles of a right triangle are
complementary.
 There can be at most one right or obtuse angle
in a triangle (Euclidian Geometry)
A
B
m<A + m<B + m<C = 180° ΔSum Thrm
m<A + 90° + m<C = 180° Subst.
C
m<A + m<C = 90° Add/Sub
Flow Proofs
• Flow proofs are the 2nd and last formal proof
that we will study.
• Similarities with the two column proof is that
each element has a statement and reason.
• Two column proofs work well for “linear”
type proofs – in other words, one step
follows another, etc.
• Flow proofs work better for “non-linear”
proofs – in other words, the order is less
defined.
Old Proof
A
B
C
Given: AB = CD
Prove AC = BD
D
BC = BC
Reflexive
AB = CD
Given
AB + BC = AC
BC + CD = BD
SAP
AB + BC = BC + CD
Add/Subt
AC = BD
Substitution
4.3 Congruent Triangles
Congruent Triangles
• Definition of Congruent Segments – Are
Segments that have the same measurement.
• There is only one measurement for a segment.
• How many parts are in a triangle?
• Six? Three segments and three angles.
• So, Congruent Triangles are triangles where all
SIX corresponding parts are congruent.
• CPCTC – Corresponding Parts of Congruent
Triangles are Congruent.
Congruent Triangles
A
O
T
C
G
D
CAT  DOG
Δ congruency statement
C D
A O
T G
CA  DO
AT  OG
TC  GD
Important Concepts
• Unlike the order of the letters of an angle,
the order of the letters of the triangles
matters.
• <ABC is congruent to <CBA
• ΔABC may or may not be congruent to
ΔCBA b/c <A may not be congruent to <C
etc….
• When you write a triangle congruency
statement make sure the corresponding
parts in fact are congruent.
Properties of Triangle
Congruence
• Reflexive:
 ΔABC is congruent to ΔABC
• Symmetric:
 If ΔABC is congruent to ΔXYZ, then ΔXYZ is
congruent to ΔABC.
• Transitive:
 If ΔABC is congruent to ΔXYZ, and ΔXYZ is
congruent to ΔLMN, then ΔABC is congruent to
ΔLMN.
4.4 Proving Congruence –
SSS and SAS
Shortcuts
• Previously – in order to prove triangles were
congruent to each other you needed to
prove all three sets of angles and all three
sets of sides were congruent.
• There are 8 shortcuts that can be used to
prove triangles congruent.
• Today we’re going to use two of them:
 SSS (Side – Side – Side)
 SAS (Side – Angle – Side)
SSS
• SSS – If the three sides of one triangle are
congruent to the three sides of another
triangle, then the triangles are congruent.
N
T
R
S
L
RST  LMN
M
SAS
• SAS – If two sides and one included angle
of one triangle are congruent to the two
sides and one included angle of the other
triangle, then the triangles are congruent.
N
T
R
S
L
RST  LMN
M
Important Concepts
• In the order of the proof you must have
three sets of congruent marks (for sides
and/or angles) BEFORE you can say that
the triangles are congruent.
• Once you say that the triangles are
congruent, then you can say that any other
part of the triangle can be congruent by
CPCTC.
Example
N
T
S
R
L
RS  LM , ST  NM ,
RT  NL
RST  LMN
R L
M
Given
SSS
CPCTC
Flow Proof
• Hints: Make each piece of the given it’s
own line down.
• Make the stuff you can get from the pictures
(Vert Angles, LP, SAP, AAP, etc..) their own
line down too.
• See example on next slide.
Example
D
Given:
DB is an
bis of
AD  DC
Prove:
A
B
C
AB  BC
ADC
4.5 Proving Triangles
Congruent by ASA and AAS.
ASA and AAS
• There are two more ways to prove triangles are
congruent.
• ASA (Angle – Side – Angle) – If two angles and
the included side of one triangle are congruent
to two angles and an included side of another
triangle, then the triangles are congruent.
• AAS (Angle – Angle – Side) If two angles and a
non included side of one triangle are congruent
to two angles and a non included side in another
triangle, then the triangles are congruent.
Example ASA
Z
X
XYZ  LMN
Y
N
L
M
Here we have two sets of
congruent angles that are
congruent along with the
included sides that are
congruent, therefore the
two triangles are
congruent by ASA.
Example AAS
Z
X
XYZ  LMN
Y
N
L
M
Here we have two sets of
congruent angles that are
congruent along with the
non included sides that
are congruent, therefore
the two triangles are
congruent by AAS.
Important Reminders
• If you’re trying to prove triangles congruent, you
MUST have three sets of corresponding parts
that are congruent BEFORE you can say that the
triangles are congruent. (SSS, SAS, ASA and
AAS)
• If you don’t have three sets of parts that are
congruent, you can’t prove the triangles
congruent.
• After you prove the triangles congruent, you can
use CPCTC to prove any of the unused parts
congruent.
General Flow Proof
X L
?
XY  LM
?
XYZ  LMN
ASA
Z N
CPCTC
Y M
?
Proving Right Triangles
Congruent
Four Additional Ways
• I told you there were 8 short cuts to proving
triangles congruent.
• Four ways that work for all triangles are SSS,
SAS, ASA and AAS.
• The other four ways work for Right Triangles
only.
• They are HA, LL, LA, and HL.
• S was for sides, and A was for angles.
• H is for Hypotenuse, L is for Leg and A is for
ACUTE angle.
Process
• Notice that these four ways, HA, LL, LA,
and HL only have two letters.
• That means you only need two sets of
congruent marks to prove Right Triangles
congruent.
• However, you need to tell me that they’re
right triangles too.
• So, you still need three things…. Two sets
of congruent marks on Right Triangles.
Examples
HA – Hypotenuse Acute Angle
LL – Leg Leg
LA - Leg Acute Angle
HL – Hypotenuse Leg
Similarities
• You will notice that SAS looks like LL if the
sides are the legs.
• ASA looks like LA.
• AAS can look like HA or LA
• HL is the only Right Triangle Congruency
Theorem that can not have a similar “all
triangle” way to prove the triangles are
congruent.
Right Triangle Flow Proof
X L
?
XY  LM
?
XYZ and
are Rt ' s
XYZ  LMN
(HA, LL, LA HL)
Z N
CPCTC
?
LMN
4.6 Isosceles Triangles
Parts of Isosceles Triangles
• Def – A triangle with two or more sides
congruent.
• The parts have special names.
C
The Congruent Sides are called
the Legs
The included angle made by the
legs is the Vertex Angle
The angles opposite the legs
are called the base angles
A
B
The side opposite the vertex is the Base
Parts of Isosceles Triangles
• The key thing to remember is this:
• It doesn’t matter which way the triangle is
oriented, the parts are all in relationship to
the congruent sides.
• The Base is not on the bottom!
• The Vertex is not on the top!
Isosceles Triangle Theorem
B
ΔABC is Isosceles, with <B as the Vertex.
Legs AB and BC are Congruent.
Draw Auxiliary Line from B to D (D is MP of
Segment AC.
Segment AD is Congruent to DC (MP Thrm)
A
D
C
Segment BD is Congruent to itself (Ref)
is Congruent
to ΔCBD (SSS)
If Two sides of ΔABD
a triangle
are congruent,
then the angles<A
opposite
those
are congruent
is Congruent
to sides
<C (CPCTC)
IF Δ
then
Δ
Converse of Isosceles Δ Thrm
• The Converse of the Isosceles Triangle
Theorem is also true.
• If two angles of a triangle are congruent,
then the sides opposite them are congruent.
If..
then…
Triangle Corollaries
• A triangle is equilateral if and only if it is
equiangular.
• Each angle of an equilateral triangle
measures 60°
Equilateral Triangles
• Since an Equilateral Triangles are also
Isosceles, each of the vertices of the
triangle are Vertex angles.
• Each side is a Leg and a Base.
• All the properties of Isosceles Triangles
exist for Equilateral Triangles as well.