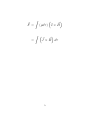Download Magnetostatics The force on a moving charged particle A particle

Magnetostatics
The force on a moving charged particle
A particle with charge Q moving with
~ is
velocity ~v in a magnetic field B
subject to a force
~
F~mag = Q ~v × B
~
If there is also an electric field E
present, then
~ + ~v × B
~
F~ = Q E
This is called the Lorentz Force Law.
75
The force on a line current
An electric current is just a large
number of moving electric charges.
Since moving charges in a magnetic
field experience a force, so too must a
current
A line charge λ C/m travelling down a
wire with velocity ~v constitutes a
current of
I~ = λ~v
76
The principle of superposition applies,
so
F~ =
=
Z
~
(λdl) ~v × B
Z ~ dl
I~ × B
77
The force on a volume current flow
Consider a charge distribution of
ρ C/m3, moving with velocity ~v .
If da is a small rectangular element of
area da which is perpendicular to the
current flow, then
~
d
I
J~ =
da
It’s the current per unit area (A/m2)
J~ = ρ~v
The magnetic force on a volume
current is then
78
F~ =
=
Z
~
(ρdτ ) ~v × B
Z ~ dτ
J~ × B
79
Moving charges create magnetic fields.
In the case of a steady electric current
~ the resulting magnetic field is given
I,
by the Biot-Savart Law . . .
Z ~ ~
µ0 I × R
~
~
B(P ) =
dl
3
4π
R
where µ0 is the permeability of free
space,
µ0 = 4π 10−7 N/A2
and where the integration is along the
current path
80
Example
Find the magnetic field a distance z
above a long straight wire carrying a
steady current I~
Z 1
µ
~
~ = 0
I~ × R
dl
B
3
4π
R
~ points out of the page
I~ × R
~ = IR sin φ = IR cos θ
I~ × R
z
dθ
l = z tan θ ⇒ dl =
2
cos θ
81
z
R
1
cos2 θ
cos θ =
⇒ 3= 2=
R
R
R
z2
µ0 I
B=
4π
Z
cos2 θ
z2
(cos θ)
!
z
dθ
2
cos θ
Z θ2
µ0 I
=
cos θdθ
4πz θ1
µ0 I
=
(sin θ2 − sin θ1)
4πz
For an infinite wire, θ1 = −π/2 and
θ2 = +π/2 so
µ0 I
B=
2πz
82
Example
Find the force of attraction between
two long parallel wires a distance d
apart, carrying currents of I1 and I2.
We showed previously that
µ0I1
B=
2πd
F~ =
F = I2B
Z
Z
~
I~ × Bdl
µ0I1I2
dl =
2πd
83
Z
dl
So the force per unit length is
I2B
Z
µ0I1I2
dl =
2πd
84
Example
Find the magnetic field a distance z
above the center of a circular loop of
radius r which carries a steady current
I
Use the Biot-Savart Law, . . .
Z ~ ~
µ0 I × R
dl
B=
3
4π
R
The horizontal components cancel.
Z
µ0 IR cos θ
dl
B=
3
4π
R
85
µ0I cos θ
=
4πR2
Z
dl
2πr2
µ0I cos θ
=
4π (z 2 + r2)3/2
86
The Continuity Equation
The Divergence Theorem says that
Z
sur
~ =
J~ • da
Z
vol
~
(∇ • J)dτ
Since charge is conserved, whatever
flows out through the surface must be
at the expense of the amount of charge
enclosed.
Z
Z
d
~
(∇ • J)dτ = −
ρdτ
dt vol
vol
Z
∂ρ
=−
dτ
vol ∂t
Since this holds for any voloume,
87
∂ρ
~
∇•J =−
∂t
This is called the continuity equation.
Magnetostatics deals with the case
where all currents are steady,
unchanging,
∇ • J~
88
The Div of B
~ =0
∇•B
This is a consequence of the
Biot-Savart Law. The proof is
starightforward, but tedious.
The Curl of B
For an infinte wire, we had
µ0 I
B=
2πz
Integrate B around a circle with the
wire as center.
Then, the path points in the same
~
direction as B
89
Z
~
~ • dl
B
=B
Z
dl
= µ0I = µ0Ienc
This holds much more generally.
Ienc =
Z
sur
~
J~ • da
From the curl theorem,
Z
path
~ =
~ • dl
B
Z
sur
~
~ • da
∇×B
= µ0Ienc
90
= µ0
Z
sur
~
J~ • da
Since this holds for any surface,
~ = µ0J~
∇×B
91
Magnetic Forces do no Work
Consider a particle with charge Q
moving with velocity ~v in a magnetic
~ It is subject to a force
field B.
~
F~mag = Q ~v × B
The work done ∆W in moving a
~ is
distance ∆l
Work done = force * distance
~
~ • ∆l
∆W = Q(~v × B)
~ • ~v ∆t
= Q(~v × B)
~ is perpendicular to ~v ,
Since ~v × B
~ • ~v = 0 so ∆W = 0
then (~v × B)
92
Vector Potential
~ = 0 then by Theorem 2, it
Since ∇ • B
must be the curl of something.
~ =∇×A
~
So B
~ is called the vector potential.
A
~ To fully
This fixes the curl of A.
~ its divergence must be
specify A,
~ so that
given. Choose A
~=0
∇•A
Recall that if φ is a scalar field, then
∇ • (∇φ) = ∇2φ
93
where the Laplacian operator is
2
2
2
∂
∂
∂
∇2 = 2 + 2 + 2
∂x
∂y
∂z
The Laplacian takes scalar fields to
scalar fields.
We now extend this notation to vector
~ where
fields. For a vector field A,
~ = Ax~i + Ay~j + Az~k
A
~ to be
we define the Laplacian of A
2A
2A
2A
∂
∂
∂
y
z ~
x
~=
~i +
~j +
k
∇2 A
2
2
2
∂x
∂y
∂z
It is straightforward (but tedious) to
show that
~ = ∇(∇ • A)
~ − ∇2 A
~
∇ × (∇ × A)
94
~ = µ0J~
Since ∇ × B
~ = µ0J~ then
and B
~ = µ0J~
∇ × (∇ × A)
~
~ − ∇2 A
= ∇(∇ • A)
~ then
Since ∇ • A
~ = −µ0J~
∇2 A
This is just Poisson’s equation
(or three Poisson’s equations, one for
each vector direction).
95
Some Terminology
~ is called the Electric Field Intensity
E
~ = 0 E
~ is called the Electric Flux
D
Density
~ is called the Magnetic Flux Density
B
~ = B/µ
~ 0 is called the Magnetic
H
Field Intensity
~ = µ0 H
~
So B
Most materials obey the laws of
electrostatics and magnetostatics,
provided that 0 and µ0 are replaced
by other constants and µ, which
depend on the material.
96
There are exceptions,
when the material’s molecules are
electrically or magnetically active, and
when the materials’ properties vary
with direction, as in crystals.
97
Summary of Electrostatics
~
F~ = QE
1
~
E=
4π0
Z
~
ρR
dτ
3
R
Alternatively, (consequences)
ρ
~
∇•E =
0
~ = 0,
∇×E
I
Z
~ = 0,
~ • dl
E
98
Qenc
~
~
E • da =
0
Alternatively, (consequence)
~ = −∇V
E
ρ
2
∇ V =−
0
1
V =
4π0
99
Z
ρ
dτ
R
Summary of Magnetostatics
F~ =
Z
~
J~ × Bdτ
Z ~ ~
µ0 J × R
~
B=
dτ
3
4π
R
Alternatively, (consequences)
~ = µ0J,
~
~ =0
∇×B
∇•B
Z
~ = µ0Ienc,
~ • dl
B
100
Z
~ =0
~ • da
B
Alternatively, (consequence)
~ =∇×A
~
B
~ = −µ0J~
∇2 A
Z ~
µ0
J
~
A=
dτ
4π R
101