Download Math 3329-Uniform Geometries — Lecture 03 1. Right angles Euclid

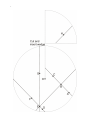
Math 3329-Uniform Geometries — Lecture 03
1. Right angles
Euclid defines a right angle as follows
When a straight line set up on a straight line makes the adjacent angles equal to one another,
each of the equal angles is right, and the straight line standing on the other is called a
perpendicular to that on which it stands.
1.1. Quiz.
–1– Draw a picture of this.
Euclid’s Fourth Postulate states
That all right angles are equal to one another.
Taking (straight) lines and geodesics as being the same, this property is shared by all smooth surfaces. It
roughly means that there has to be 360◦ around every point (or at least the same number of degrees), which
isn’t necessarily true on a cone. In the first model at the end of these lecture notes, we have a cone formed
by adding a 90◦-wedge leaving 450◦ around the vertex. The geodesic shown through A, O, and B is OK,
because there are 225◦ degrees on either side. As long as there are at least 180◦ on either side, we’d be
OK. The ray OC cuts the 225◦ in half, so here, we have two right angles that measure 112.5◦. Taking other
geodesics through the vertex, we could get right angles that measure anything from 90◦ to 135◦.
Euclid’s Fourth Postulate is his statement that points like this don’t exist in his universe. He probably
couldn’t imagine such a thing, but he somehow found it important to mention. Now that we know about
things like black holes, we should be ready embrace cone points and worse.
2. Parallel lines
Euclid’s 23rd definition defines parallel lines.
Parallel straight lines are straight lines which being in the same plane and being produced
indefinitely in both directions, do not meet one another in either direction.
This probably seems intuitive, but I think most of us more strongly associate parallel with equidistant. I’m
glad that Euclid chose this definition, because it inspired some really cool stuff later on. The same goes for
Euclid’s Fifth Postulate.
That, if a straight line falling on two straight lines make the interior angles on the same side
less than two right angles, the two straight lines, if produced indefinitely, meet on that side
on which are the angles less than the two right angles.
Look at the second paper model. The line BE falls on the lines AC and EG. The angle ∠CBE = 90◦
and the angle ∠BEG = 45◦ , which sum to less than two right angles (180◦). In the plane, of course, we
would expect the lines AC and EG to intersect. On this cone, however, this does not happen. It is not
the sharpness of the cone point that makes this happen in this case. We could, for example, smooth off the
cone point without changing the rest of the geometry. This is a manifestation of curvature. Euclid’s Fifth
Postulate, therefore, is saying that Euclid’s universe has no curvature. We know that our universe has at
least some curvature, so we’ll want to understand that to some extent.
1
2
2.1. Quiz.
–1– What does Euclid’s Fifth Postulate say, if the interior angles make exactly two right angles? more
than two right angles?
–2– The two examples of cones today were formed by adding a wedge. Does Euclid’s Fifth Postulate
hold on a cone formed by removing a wedge?
2.2. Homework.
–1– Make a model of a cone with a removed 90◦ wedge. Describe what happens, in general, when you
try to make parallel lines with the cone point between the two lines.
3
4
5
References
[Bonola]
Roberto Bonola (1955). Non-Euclidean Geometry (H.S. Carslaw, Trans.). Dover Publications, New York. (Original
translation, 1912, and original work published in 1906.)
[Descartes] Rene Descartes (1954). The Geometry of Rene Descartes (D.E. Smith and M.L. Latham, Trans.). Dover Publications, New York. (Original translation, 1925, and original work published in 1637.)
[Euclid]
Euclid (1956). The Thirteen Books of Euclid’s Elements (2nd Ed., Vol. 1, T.L. Heath, Trans.). Dover Publications,
New York. (Original work published n.d.)
[Eves]
Howard Eves (1990). An Introduction to the History of Mathematics (6th Ed.). Harcourt Brace Jovanovich, Orlando, FL.
[Federico] P.J. Federico (1982). Descartes on Polyhdra: A study of the De Solidorum Elementis. Springer-Verlag, New York.
[Henderson] David W. Henderson (2001). Experiencing Geometry: In Euclidean, Spherical, and Hyperbolic Spaces 2nd Ed.
Prentice Hall, Upper Saddle River, NJ.
[Henle]
Michael Henle (2001). Modern Geometries: Non-Euclidean, Projective, and Discrete 2nd Ed. Prentice Hall, Upper
Saddle River, NJ.
[Hilbert]
David Hilbert (1971). Foundations of Geometry (2nd Ed., L. Unger, Trans.). Open Court, La Salle, IL. (10th
German edition published in 1968.)
[Hilbert2]
D. Hilbert and S. Cohn-Vossen (1956). Geometry and the Imagination (P. Nemenyi, Trans.). Chelsea, New York.
(Original work, Anschauliche Geometrie, published in 1932.)
[Motz]
Lloyd Motz and Jefferson Hane Weaver (1993). The Story of Mathematics. Avon Books, New York.
[Weeks]
Jeffrey R. Weeks (1985). The Shape of Space. Marcel Dekker, New York.