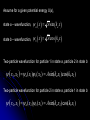Download Document

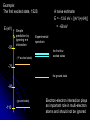
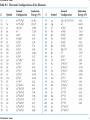
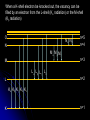
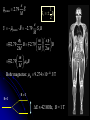
自旋—軌道作用
internal magnetic field
The spin-orbit interaction
In the absence of an external magnetic field, internal field generated
by electron motion (proportional to orbital angular momentum) will
interact with spin dipole moment
Frame of electron
 LB
S
when L is parallel to S
Frame of nucleus

S
e

L
Ze
Ze
e
s
Nucleus circulates around electron
 a B-field due to the nuclear motion
Orbital dipole moment is anti-parallel to
spin dipole moment
higher energy
U    s  B  0
state
(spin up)
Frame of electron
when L is anti-parallel to S
s
Frame of nucleus
Ze
e
Ze

S
2p3/2
2p1/2
1s
(l = 0, |L| = 0)

S
Nucleus circulates around electron
 a B-field due to the nuclear motion
Orbital dipole moment is parallel to spin
dipole moment
(l = 1, |L| > 0)
2p
e
LB
 
L S 
s

 S
s
U   s  B  0 lower energy
state
(spin
down)
The spin-orbit interaction
causes fine structure doubling
of atomic spectral lines
(3/3/2010)
Total angular momentum (as a result of spin-orbit interaction)
J  LS
magnitude:
J 
j  j  1
z-component: J z  m j
m j   j,  j  1, , j  1, j
Neither L nor S is conserved separately!
Permissible values for the total angular momentum quantum number j
j  l  s, l  s  1, , | l  s |
(maximum
value)
For an atomic electron s = 1/2
1
1
jl , l
2
2
(minimum
value)
Example,
for the 2p state l = 1, j = 3/2 or 1/2
for the 3d state l = 2, j = 5/2 or 3/2
for the s state l = 0, j = 1/2
l=1
j = 1/2
3
| J |
2
1 1
mj   ,
2 2
j = 3/2 | J |
15
2
3 1 1 3
mj   , , ,
2 2 2 2
mj has an even number of values
(a) A vector model for determining the total angular momentum J = L + S of a
single electron
(b) The allowed orientations of the total angular momentum J for the states j = 3/2
and j = 1/2. Notice that there are now an even number of orientations possible,
not the odd number familiar from the space quantization of L alone
Energy shift due to spin-orbit interaction
Square of total angular momentum

J  LS
2
  L  S L  S 
U LS   s  Binternal
Binternal  ?
2
 L2  S 2  2 L  S
J 2  L2  S 2
LS 
2
Spin-orbit interaction energy (a relativistic effect):
U LS

Ze2 ge
1

LS
2 2 3
4 o 2 4me c r
U LS  L  S 
2
 j  j  1 
2

U

U
Write
LS
o  j  j  1 



r: radius of the orbiting electron
c: speed of light

 1  s( s  1) 
3
 1  
4
Spin-orbit energy shift
2P3/2
3
1
j  , l  1, s 
2
2
2P1/2
1
1
j  , l  1, s 
2
2
2S1/2
1
1
j  , l  0, s 
2
2
e.g., For a hydrogen atom
Uo = 1.510-5 eV

U LS  U o  j  j  1 

ms=1/2
(n = 2)
3
1  1 
E  2P1/ 2   E2  U o    1  11  1    E2  2U 0
4
2  2 
3
1  1 
E  2S1/ 2   E2  U o    1  0  0  1    E2
4
2  2 
B=0
(2) 2S1/2
(8)
n1
2  2  1
0
3
 1  
4
3
3 3 
E  2P3/ 2   E2  U o    1  11  1    E2  U 0
4
2  2 
(4) 2P3/2
2S, 2P

(2) 2P1/2
B0
(but small)
mj
3/2
1/2
1/2
3/2
1/2
1/2
1/2
1/2
Remarks:
In a small external B field, the spin-orbit interaction is dominant
and the total angular momentum J as a whole precesses
around the B field. The no. of split lines = the no. of mj values
In a large external B field, both the orbital angular momentum L
and the spin angular momentum S precess independently
around the B field. The no. of splitting lines = 2  (2l + 1)
Quantum numbers – in the absence of spin-orbit effect, a state
of an atomic electron is specified by (n, l, ml, ms). If the spin-orbit
interaction is taken into account, the state may be specified by
(n, l, j, mj)
2P3/2, 2P1/2, 2S1/2
Example: electronic states associated with the principle quantum
number n = 2
(n, l , ml , ms )
( n, l , j , m j )
1

 2,0,0,  ,
2

1

2,1,0,

,
2

1 1

2,0,
, ,

2 2

3 3

2,1,
, ,

2 2

1

 2,0,0,  
2

1

2,1,0,



2

1 1

2,0,
, 

2 2

3 1

2,1,
, 

2 2

1 
1

2,1,1,
,
2,1,1,


 

2 
2

1 
1

2,1,

1,
,
2,1,

1,


 

2 
2

3 1 
3 3

2,1,
,

,
2,1,
, 

 
2 2 
2 2

1 1 
1 1

 2,1, ,  ,  2,1, ,  
2 2 
2 2

(in the absence of spin-orbit
interaction)
(in the presence of spin-orbit
interaction)
Weak B field
Strong B field
The angular momentum vectors L, S,
and J for a typical case of a state with
l = 2, j = 5/2, mj = 3/2.
The vectors L and S precess uniformly
about their sum J, as J precesses
randomly about the z axis
In a strong B field, the
orbital angular momentum
L precesses about the z
axis.
(Similarly for the spin
angular momentum S )
(3/8/2010)
Pauli Exclusion Principle
Pauli (1900–1958)
From spectra of complex atoms, Pauli (1925) deduced a new rule:
In a given atom, no two electrons can be in the same quantum
state, i.e. they cannot have the same set of quantum numbers
n,,m,ms
Every “atomic orbital with n,,m” can hold two electrons:
(n,,m,) and (n,,m,)

Thus, electrons do not pile up in the lowest energy state, i.e, the (1,0,0)
orbital
 They are distributed among the higher energy levels according to
the Pauli Principle
 Particles that obey Pauli exclusion principle are called “fermions”
More generally, no two identical fermions (any particle with spin of ħ/2,
3ħ/2, etc.) can be in the same quantum state
Two-particle problems
– Consider two particles in a one-dimensional potential well U = U(x)
There exist a series of eigenstates
Quantum state labels: a, b, c, ……
Eigenfunctions: a(x), b(x), c(x), ……
Eigenvalues: Ea, Eb, Ec, ……
e.g., one-particle problem – if there is only one particle in the potential well
and the particle is in the state a
2
d2

 a  x   U ( x ) a  x   Ea a  x 
2
2m dx
Write: H a  x   Ea a  x 
H: Hamiltonian
Now consider two particles, 1 and 2, in the potential well. Assume
particle 1 be in the state a and particle 2 be in the state b
2
d2

 a  x1   U ( x1 ) a  x1   Ea a  x1 
2
2m dx1
2
d2

 b  x2   U ( x2 ) b  x2   Eb b  x2 
2
2m dx2
H ( x1 ) a  x1   Ea a  x1 
H ( x2 ) b  x2   Eb b  x2 
Guess: the total wavefunction for this two-particle system
2


d2
 2 d2
  2m dx 2  U ( x1 )  2m dx 2  U ( x2 )   x1 , x2 
1
2


  H ( x1 )  H ( x2 )   x1 , x2 
  H ( x1 )  H ( x2 )  a  x1  b  x2 
 Ea a  x1   b  x2    a  x1   Eb b  x2 
 ( Ea  Eb ) a  x1  b  x2 
 ( Ea  Eb )  x1 , x2 
The wavefunction for
particle 1 in state a and
particle 2 in state b
 (x1,x2) = a(x1)b(x2)
is a solution, with the total
energy E = Ea + Eb
Now let the positions of the two particles be exchanged. Let
particle 2 be in the state a and particle 1 be in the state b
2
d2

 a  x2   U ( x2 ) a  x2   Ea a  x2 
2
2m dx2
H ( x2 ) a  x2   Ea a  x2 
2
H ( x1 ) b  x1   Eb b  x1 
d2

 b  x1   U ( x1 ) b  x1   Eb b  x1 
2
2m dx1
Guess: the total wavefunction for this two-particle system
The wavefunction for particle 2 in
 H ( x2 )  H ( x1 )  x2 , x1 
state a and particle 1 in state b
  H ( x2 )  H ( x1 ) a  x2  b  x1 
 Ea a  x2   b  x1    a  x2   Eb b  x1   (x ,x ) =  (x ) (x )
2 1
a 2
b 1
 ( Ea  Eb ) a  x2  b  x1 
is a solution, with the total
energy E = Ea + Eb
 ( Ea  Eb )  x2 , x1 
Assume for a given potential energy U(x),
state a – wavefunction,
 a  x   A sin  ka x 
state b – wavefunction,
 b  x   A cos  kb x 
Two-particle wavefunction for particle 1 in state a, particle 2 in state b
  x1, x2    a ( x1 ) b ( x2 )  Asin(ka x1 )cos(kb x2 )
Two-particle wavefunction for particle 2 in state a, particle 1 in state b
  x2 , x1    a ( x2 ) b ( x1 )  Asin(ka x2 )cos(kb x1 )
“Probability density” for particle 1 in state a and particle 2 in state b
P  x1, x2  |  x1, x2  | | A | sin (ka x1 )cos (kb x2 )
2
2
2
2
“Probability density” for particle 2 in state a and particle 1 in state b
P  x2 , x1  |  x2 , x1  | | A | sin (ka x2 )cos (kb x1 )
2
2
2
2
The guess solutions (x1,x2) = a(x1)b(x2) and (x2,x1) = a(x2)b(x1) imply
that the “probability density” for finding the two particles is not the same
under exchange of the two particle coordinates
P  x2 , x1   P  x1, x2 
Can measurable physical quantities
be differing under particle exchange ?
Quantum particles are “indistinguishable” –
a purely quantum-mechanical concept; no classical analogy !
The scattering of two electrons as a result of their mutual repulsion. The events
depicted in (a) and (b) produce the same outcome for identical electrons but are
nonetheless distinguishable classically because the path taken by each electron is
different in the two cases. In this way, the electrons retain their separate identities
during collision. (c) According to quantum mechanics, the paths taken by the
electrons are blurred by the wave properties of matter. In consequence, once they
have interacted, the electrons cannot be told apart in any way!
Electrons are identical particles. It is impossible to distinguish one
electron from another ! Also, wavefunctions can overlap !!
 a(x1)b(x2) and a(x2)b(x1) are not the correct wavefunctions
 Need to search for the right wavefunctions ?!
Exchange Symmetry
The simplest case: Two identical (“indistinguishable”) particle system
Consider two identical particles satisfying 3D Schrödinger equations
with coordinates r1 and r2. Assume no interaction between them


2
2m
2
2m
12 a  r1   U  r1  a  r1   Ea a  r1   H  r1  a  r1 
22 b  r2   U  r2  b  r2   Eb b  r2   H  r2  b  r2 
 H  r1   H  r2   r1 , r2   E  r1 , r2 
  r1, r2    a  r1  b  r2 
Particle 1 has energy Ea and particle 2 has energy Eb. E = Ea + Eb
exchange particles r1  r2
  r2 , r1    a  r2  b  r1 
A distinguishable solution !
Particle 1 has energy Eb and particle 2 has energy Ea
Try linear combinations of the two wavefunctions:
1
 S  r1 , r2  
 a  r1  b  r2   a  r2  b  r1  
2
S is a solutions
of the (linear)
Schrödinger eq.
with E = Ea + Eb
 H  r1   H  r2  S  r1 , r2 
1
  H  r1   H  r2 
 a  r1  b  r2    a  r2  b  r1 
2
1

 H  r1  a  r1  b  r2   H  r1  a  r2  b  r1 
2
1

 H  r2  a  r1  b  r2   H  r2  a  r2  b  r1 
2
1

 Ea a  r1  b  r2   Eb a  r2  b  r1 
2
1

 Eb a  r1  b  r2   Ea a  r2  b  r1 
2
1
  Ea  Eb 
 a  r1  b  r2    a  r2  b  r1   ( Ea  Eb ) S (r1 , r2 )
2
Try linear combinations of the two wavefunctions:
1
 A  r1, r2  
 a  r1  b  r2   a  r2  b  r1  
2
A is a solutions
of the (linear)
Schrödinger eq.
with E = Ea + Eb
 H  r1   H  r2  A  r1 , r2 
1
  H  r1   H  r2 
 a  r1  b  r2   a  r2  b  r1 
2
1

 Ea a  r1  b  r2   Eb a  r2  b  r1 
2
1

 Eb a  r1  b  r2   Ea a  r2  b  r1 
2
1
  Ea  Eb 
 a  r1  b  r2   a  r2  b  r1 
2
 ( Ea  Eb ) A ( r1, r2 )
Under exchange of particle coordinates r1  r2
1
symmetric
 S  r1,r2  
 a  r1  b  r2    a  r2  b  r1 
2
1
 S  r2 , r1  
 a  r2  b  r1    a  r1  b  r2    S  r1 , r2 
2
1
anti-symmetric
 A  r1 , r2  
 a  r1  b  r2   a  r2  b  r1 
2
1
 A  r2 , r1  
 a  r2  b  r1   a  r1  b  r2    A  r1 , r2 
2
Both satisfy the Exchange Symmetry Principles
 S  r1, r2    S  r2 , r1  ,  A  r1, r2    A  r2 , r1 
2
2
2
2
No observable
difference !!
Exchange symmetry: For both S and A, all the probability densities
(observable effects) are unaffected by the interchange of particles
A two-electron system: the helium atom He

 a r1 

2
2me
4 o r1
 a  r1   Ea a  r1 
H  r1  a  r1   Ea a  r1 
2e+

 b r2 
12 a  r1  
2e 2
2
2
2
e

22 b  r2  
 b  r2   Eb b  r2 
2m
4 o r2
H  r2  b  r2   Eb b  r2 
 S  r1 , r2  
1
 a  r1  b  r2    a  r2  b  r1 
2
1
 A  r1 , r2  
 a  r1  b  r2   a  r2  b  r1 
2
symmetry space
wavefunction
anti-symmetric
space wavefunction
Total two-particle wavefunction:
(r1 , r2 )   space  r1, r2   spin (, )
A
describes a class of particles called “fermions”
 A (r1 , r2 )   A ( r2 , r1 )
S
describes a class of particles called “bosons”
 S ( r1 , r2 )   S ( r2 , r1 )
(Both the spatial
coordinates and the
spin orientations of
the two particles are
to be simultaneously
interchanged)
Pauli exclusion principle states that no two electrons in an atom can
have the same set of quantum numbers (no two electrons can
occupy the same quantum state). The exclusion principle applies
only to fermions
It is an experimental fact that integer spin particles are bosons, but
half-integer spin particles are fermions
The symmetry character of various particles
particle
symmetry
Spin (s)
Electron
antisymmetric
1/2
Fermions（費米子）
Positron
antisymmetric
1/2
Proton
antisymmetric
1/2
half-integer spin
particles
Neutron
antisymmetric
1/2
Muon
antisymmetric
1/2
 particle
symmetric
0
Bosons（玻思子）
He atom (G)
symmetric
0
integer spin particles
 meson
symmetric
0
Photon
symmetric
1
Deuteron
symmetric
1
e.g., Helium isotope 3He (2 protons + 1 neutron) – a fermion
Example 9.5 Ground state of the helium atom
Construct explicitly the two-electron ground state wavefunction for
the helium atom in the independent particle approximation
(Assume each helium electron sees only
the doubly charged helium nucleus)
Hydrogen-like atom with the lowest energy, Z = 2
1 2
 100  r   R10 ( r )Y00 ( ,  ) 
 
  ao 
3/ 2
e 2 r ao
E1 =  2213.6
=  54.4 eV
1
 S  r1 , r2  
 100 ( r1 ) 100 ( r2 )   100 ( r2 ) 100 ( r1 )
2
3
2  2  2( r1  r2 ) / a0

  e
  a0 
symmetric spatial
wavefunction
Spin eigenfunctions for two-electron systems
Singlet state (單重態), S = 0, ms = 0


1
1
A 
| | 
| ,  | ,  
2
2
Linear
combinations
of
|, |
|, |
anti-symmetric spin wavefunction
Triplet state (三重態), S = 1, ms = 0, 1

|
| , 



 1
 1
S  
| |  
| ,  | ,  
 2
 2


|
| , 

ms=1
ms=0

symmetric spin wavefunction
ms=1
Total two-electron wavefunction for a helium atom
The ground state – only once choice: 1S2, spin singlet (total spin = 0)
 A ( r1 , r2 )   S ( r1 , r2 )   A
3
1  2  2( r1  r2 ) / a0
   e
 | ,   | , 
  a0 
The equal admixture of the spin states |+ and |+ means the spin
of the first helium electrons is just as likely to be up as it is to be
down
The spin of the second electron must always be opposite the first
If both electrons had the same spin orientations  A = 0. The
theory allows no solution  no two electrons can occupy the same
quantum state
Energy for the two electrons in a helium atom
A naïve estimate:
E = 2  ( Z213.6 eV) = 108.8 eV,
with Z = 2, n = 1
Remarks:
In practice, it requires only 24.6 eV to remove the first electron. To
remove the second electron requires 54.4 eV. The electron left
behind screens the nuclear charge and make the ionization of the
first electron easier
The other possible choice of wavefunction A(r1,r2) = A(r1,r2)triplet
must comprise a higher energy eigenstate
symmetric under
spin exchange
Example:
The first excited state, 1S2S
A naive estimate:
E = 13.6 eV  [(4/1)+(4/4)]
E (eV)
-50
= 68 eV
Simple
prediction by
ignoring e-e
interaction
(1st excited state)
Experimental
spectrum
the first four
excited states
-70
the ground state
-90
(ground state)
-110
Electron-electron interaction plays
an important role in multi-electron
atoms and should not be ignored
Hydrogen molecular ion: H2+
(Serway, Fig. 11.7)
The wavefunction (a) and probability density (b) for the approximate molecular wave
+ formed from the symmetric combination of atomic orbitals centered at r = 0 and r
= R. (c) and (d): Wavefunction and probability density for the approximate molecular
wave - formed from the anti-symmetric combination of these same orbitals
The bonding state (a), a spin singlet state, possesses a lower energy than
the anti-bonding state (c), a spin triplet state
1921 – Stern-Gerlach experiment of anomalous Zeeman effect
1925 – Pauli exclusion principle (the fourth degree of freedom)
1925 – Goudsmit-Uhlenbeck theory of electron spin
當泡利處心積慮的鑽研反常塞曼效應時，當時在慕尼黑的朋友
問他：「你為何總是愁眉苦臉的？」泡利馬上反問道：「要是
你陷入了反常塞曼效應的思慮，難道還快樂的起來嗎？」根據
當時的條件，泡利是無法圓滿的解釋這個效應的。而沿著這條
路走下去，卻使他得以發現不相容原理。
《微觀絕唱》，p.143
Ehrenfest on Goudsmit-Uhlenbeck theory:
「你們還很年輕，做點蠢事也沒有什麼關係！」
Wolfgang Pauli
Otto Stern
Lorentz
Kondo effect – a singlet ground state formed by the localized
moment and the screening conduction electron spins
Electron-electron interactions and Screening effects
Helium atom:
( e)( e)
H  r1 , r2   H  r1   H  r2  
4 0 | r1  r2 |
(??)
Each electron sees not only the attractive helium nucleus but also the
other electron
Electrons confined to the small space of an atom exert strong repulsive
electrical forces on each other (especially in multi-electron atoms)
Is the charge of nucleus = +2e from electron’s viewpoint ?
Inner electrons screen the positive charge of nucleus, and hence reduce
the effective Z and the attractive potential  smaller negative potential
energy (especially for multi-electron atoms)
The resulting effective potential energy seen by an electron in the atom
can be notably smaller than the bare potential energy
The Periodic Table
Mendeleev’s table as published in 1869 – 63 elements
Mendeleev
1834~1907
Ga
Ge
Sc
“All good theories should be able to make predictions and
this was no exception”
Build a multiple electron atom
Chemical properties of an atom are determined by the least tightly
bound electrons
Occupancy of subshell
Energy separation between the subshell and the next higher subshell
n
1
2
3
s shell
=0
Helium and Neon
and Argon are inert.
Their outer subshell
is closed
p shell
=1
Hydrogen: (n, , mℓ, ms) = (1, 0, 0, ±½) in ground state
In the absence of a magnetic field, the state ms = ½ is degenerate with the
ms = −½ state
Helium: (1, 0, 0, ½) for the first electron; (1, 0, 0, −½) for the second
electron.
The two electrons have anti-aligned spins (ms = +½ and ms = −½)
The principle quantum number has letter codes.
n=
1 2 3 4...
n = shells (e.g., K shell, L shell, …)
Letter =
K L M N…
How many electrons may be placed in each subshell?
Total
For each mℓ: two values of ms
2
For each  : (2  + 1) values of mℓ
 =
0 1 2 3 4 5 …
Letter = s p d f g h …
2(2 + 1)
n = subshells (e.g., 1s, 2p, 3d, …)
1s
1s2
1s22s
The filling of electronic
states must obey the
Pauli exclusion principle
and Hund’s rule (spinspin correlation)
1s22s2
1s22s22p1
1s22s22p2
1s22s22p3
1s22s22p4
1s22s22p5
1s22s22p6
1s22s22p63s
1s22s22p63s2
Energies of orbital subshells increase with increasing 
Energies of orbital subshells are lower for lower . Lower angular momentum
implies more eccentric classical orbits, with greater penetration into the
nuclear regime
Fill electrons to states according to the lowest value of n+, with “preference”
given to n
n+
The lower  values have more eccentric
classical orbits than the higher  values
Electrons with higher  values are more shielded
from the nuclear charge
Electrons lie higher in energy than those with
lower  values
4s fills before 3d
7s
6s
5s
4s
3s
2s
1s
7p
6p
5p
4p
3p
2p
7d
6d
5d
4d
3d
7f 7g 7h 7i
6f 6g 6h
5f 5g
4f
8
8
7
7
6
6
6
5
5
5
4
4
3
3
2
1
Groups:
 Vertical columns
 Same number of
electrons in an  orbit
 Can form similar
chemical bonds
Periods:


Horizontal rows
Correspond to filling
of the subshells
Inert Gases:




Last group of the periodic table
Closed p subshell except helium
Zero net spin and large ionization energy
Their atoms interact weakly with each other (van der Waals forces)
Alkalis:




Single s electron outside an inner core
Easily form positive ions with a charge +1e
Lowest ionization energies
Electrical conductivity is relatively good
Alkaline Earths:



Two s electrons in outer subshell
Largest atomic radii
High electrical conductivity
Halogens:



Need one more electron to fill outermost subshell
Form strong ionic bonds with the alkalis
More stable configurations occur as the p subshell is filled
Transition Metals:




Three rows of elements in which the 3d, 4d, and 5d are being filled
Properties primarily determined by the s electrons, rather than by the
d subshell being filled
Have d-shell electrons with unpaired spins
As the d subshell is filled, the magnetic moments, and the tendency
for neighboring atoms to align spins are reduced
Lanthanides (rare earths): Z = 57 ~ Z = 70



Have the outside 6s2 subshell completed
As occurs in the 3d subshell, the electrons in the 4f subshell have
unpaired electrons that align themselves
The large orbital angular momentum contributes to the large
ferromagnetic effects
Actinides:



Z = 89 ~ Z = 102
Inner subshells are being filled while the 7s2 subshell is complete
Difficult to obtain chemical data because they are all radioactive
Have longer half-lives
X-ray spectra and Moseley’s law
Target :W
Electronic transitions within the
inner shells of heavy atoms are
accompanied by emission of highenergy photons (x rays)
series of sharp lines: “characteristic
spectrum” of the target material
1913–4, Moseley measured characteristic x-ray spectra of 40 elements,
and observed “series” of x-ray energy levels, called K, L, M, … etc.
Analogous to optical series for hydrogen (e.g. Lyman, Balmer, Paschen…)
The characteristic spectrum
hole in K-shell (n = 1)
discovered by Bragg
systematized by Moseley
ejected
K-shell electron
incident
electron
scattered
incident electron
hole in L-shell
(n = 2)
The characteristic peak is created
when a hole in the inner shell created
by a collision event is filled by an
electron from a higher energy shell
x-ray
When a K-shell electron be knocked out, the vacancy can be
filled by an electron from the L-shell (K radiation) or the M-shell
(K radiation)
O
N N
N
n=5
n=4
M M M
n=3
M
L L L  L
n=2
L
K K K K K
K
n=1
K series: n = 2, 3, … to n = 1
Consider the K line. An electron in the
L shell is partially screened from the
nucleus by the one remaining K shell
electron
( Z  1)2
EL  13.6 
eV
2
n
( Z  1)2
EK  13.6 
eV
2
1
1
2

 EL  EK  13.6  1  2   Z  1 eV

 n 
hc
e.g., (K) = 0.723 Å for molybdenum
(Z = 42)
Atomic number versus square
root of frequency (Moseley, 1914)
L series: n = 3, 4, … to n = 2
2
1 1
EL 
 13.6  2  2   Z  7.4  eV

2 n 
hc
Moseley’s law: the square root of photon frequency should vary
linearly with the atomic number Z (A direct way to measure Z )
Moseley established the fact that the correct sequence of
elements in the periodic table is based on atomic number rather
than atomic mass
Nuclear Magnetic Resonance Imaging (NMRI or MRI)
MRI is a medical imaging technique used in radiology to visualize the
internal structure and function of the body. It provides great contrast
between the different soft tissues of the body, making it very useful in
brain and cancer imaging. It uses no ionizing radiation, but uses a
powerful magnetic field to align the nuclear magnetization of hydrogen
atoms in water in the body
Proton magnetic moment: (very small
compared with electron magnetic moment)
proton  2.79
e
M proton
1
Sproton , s =
2
U  proton  B  10  102 MHz
Resolution: 1 – 0.1 mm
An expensive, large-volume superconducting magnet
of several Tesla
proton
e
 2.79 S
M
1
Sz  
2
e
U   proton  B  2.79 S z B
M
e
 m  e 
 2.79
B  2.79   
B
2M
 M   2m 
m
 2.79   B B
M 
Bohr magneton: B  9.274  10 24 J/T
B0
B=0
E  42 MHz, B = 1 T
Summary:
Orbital magnetism and the normal Zeeman effect
Electron spin
The spin-orbit interaction
Exchange symmetry and the Exclusion principle
The periodic table
X-ray spectra and Moseley’s law