Download Chemical equilibrium and the kinetic theory of gases

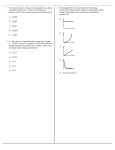
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
.
61
Chemical equilibrium
and the kinetic theory
of gases
Equilibrium processes have a central importance to industrial chemistry.
Although reactions are rarely allowed to reach equilibrium, knowledge of
the factors that influence the position of equilibrium is critical for a chemical
engineer. In this unit you will become familiar with various quantitative
methods for solving problems connected with such equilibria.
The unit begins with a study of the kinetic theory of gases because many of
the processes that are used in industry involve gaseous reactants. The ideal
gas equation, which is derived from kinetic theory, is important in allowing
chemists to be able to analyse equilibrium systems involving gases.
On successful completion of this topic:
•• you will be able to apply the concept of chemical equilibrium (LO1).
To achieve a Pass in this unit you should be able to:
•• account for the relationship between the variables in the ideal gas
equation (1.1)
•• calculate terms in the ideal gas equation (1.2)
•• write expressions for calculating chemical equilibrium constants (1.3)
•• solve problems involving chemical equilibrium (1.4).
1
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
1 The kinetic theory of gases
Chemical engineers deal with a wide range of gases as components of the systems
that they use in reactors. Knowledge of how these gases behave under different
conditions of temperature and pressure is clearly going to be very important to
a chemical engineer – and fortunately the behaviour of all gases is governed to a
large extent by an equation known as the ideal gas law.
You will see below how this law is derived from very simple principles.
The kinetic model of gases
This is a very simple model to describe the nature of gases, built on three key
assumptions:
•• gases consist of molecules in continuous random motion
•• the size of these molecules is very much smaller than the distance between
them
•• there are no forces between gas molecules (except during a collision process).
Collisions and distribution of speeds
The total kinetic energy of a sample of gas at a given temperature will be constant,
and therefore the average energy (and speed) of a gas molecule will also be
constant.
However, molecules do collide with each other and these collisions result in the
transfer of momentum and kinetic energy. As a result, the speed of individual
molecules within the gas varies from molecule to molecule.
The distribution of these speeds is described as the Maxwell distribution and is
most conveniently shown as in Figure 6.1.1, which is a plot of the fraction of
molecules possessing particular ranges of speeds.
Figure 6.1.1: The Maxwell distribution
can be used to show how the
distribution of molecular speeds
changes at different temperatures.
Relative abundance
273 K
373 K
473 K
0
200
6.1: Chemical equilibrium and the kinetic theory of gases
400
600
800
1000
1200
1400
Speed in m/s
2
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Collisions and pressure
Take it further
For more information on how
this equation is derived from
the kinetic theory and on the
idea of root mean square speed,
you could consult a physical
chemistry textbook such as
Elements of Physical Chemistry
(P. Atkins and J. de Paula, OUP,
2009). The derivation of this
equation is covered on pages
23–24 and pages 37–38.
What we usually call the pressure of a gas can be thought of as arising from the
force exerted by molecules colliding with the walls of a container.
The kinetic theory of gases allows us to calculate the pressure of a gas in terms of
the speed of the molecules, c (more strictly this is the root mean square speed):
nMc2
3V
p=
where
n = number of moles of molecule
M = molar mass of molecules
c = root mean square speed
V = volume of gas.
The ideal gas law
Gas laws
The behaviour of gases when subjected to changes of pressure, volume or
temperature can be summarised by three simple experimentally-derived
equations:
•• Boyle’s law: the pressure of a fixed mass of gas (at constant temperature) is
inversely proportional to its volume.
Hence if a gas has pressure P1 with volume V1, the new pressure P2 when the
volume is changed to V2 is given by the relationship:
(1) P1 V1 = P2V2
•• Charles’s law: the volume of a fixed mass of gas (at constant pressure) is
proportional to its absolute temperature (that is, the temperature measured
in Kelvin).
(2)
V1
T1
=
V2
T2
•• Gay-Lussac’s law (or the pressure law): the pressure of a fixed mass of gas (at
constant volume) is proportional to its absolute temperature.
P1
P2
Activity
(3)
Show how equation (4) is derived.
(Hint: start from equation (1) and
use equation (2) to substitute
in values of V1 and V2 in terms of
temperature.)
Using any two of these equations, they can be combined into one equation:
(4)
T1
=
P1 V1
T1
T2
=
P2 V2
T2
or
PV
T
= a constant
Avogadro’s law
A further experimentally derived law states that the volume of a gas is
proportional to the number of moles (n) of gas it contains.
1 mole of gas occupies 22.4 dm3 at 273 K and 1 atm pressure, so at 273 K:
V = 22.4 n
6.1: Chemical equilibrium and the kinetic theory of gases
3
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Equation of state: the ideal gas law
The ideas from the gas laws and Avogadro’s law can be combined into the ideal
gas law:
Activity
Calculate a value for R in units of
atm dm–3 K–1 mol–1 by using data
for the volume of 1 mole of a gas at
1 atm pressure and 273 K.
For 1 mole of gas
PV
T
= R, the gas constant
For n moles of gas:
PV
T
= nR, so (5) PV = nRT
R is the ideal gas constant and has a value of 8.314 J K−1 mol−1.
When the gas law is used, all the quantities must be in SI units.
The ideal gas law is described as an equation of state, describing the properties of
matter under a specific set of conditions.
Conversion to SI units
•• Pressure in Pa: 1 Pa = 9.871 × 10–6 atm = 105 bar = 0.1 Mbar.
•• Volume in m3: 1 m3 = 106 dm3 = 106 litres.
•• Temperature in K: temperature in K = temperature in °C + 273.
The ideal gas law and kinetic theory
Although the ideal gas law was first derived from experimental laws, it can be
shown to be consistent with the expression for pressure obtained from the
kinetic theory:
nMc2
1
P=
so PV = nMc2
3
3V
Since temperature is a measure of the average kinetic energy of the molecules
in the gas, ½Mc2, this equation is obviously related directly to the ideal gas
equation above.
Case study: Using the ideal gas equation
Chemical engineers may need to be able to calculate the volumes required to store or collect specified amounts
of gases (as products or reactants). The gases may be cooled (for storage) or heated (to meet the requirement for
specific reaction conditions). The ideal gas equation enables a simple prediction of these volumes to be made.
In different manufacturing locations, different units may be used for pressure, volume (and even temperature; for
instance, °F is still in common use in the USA), so before the ideal gas equation can be used, these data must be
converted into SI units.
The following calculations will give practice in applying the ideal gas equation and/or the individual gas laws. In each
case, assume that the gas is behaving ideally.
R, the gas constant = 8.314 J K−1 mol−1.
1 The volume of a gas at 10 bar pressure is 36.4 dm3. Calculate the new volume if the pressure is increased to
200 bar (temperature remains constant).
2 The volume of a gas at 24 °C is 135 dm3. Calculate the new volume if the temperature is increased to 200 °C (note:
think about the units that should be used in the calculation). The pressure remains constant.
3 Calculate the volume of 2.0 moles of gas at 400 K and 20 bar pressure.
6.1: Chemical equilibrium and the kinetic theory of gases
4
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Real gases
Although the ideal gas equation is an adequate description of the behaviour
of gases at atmospheric conditions of temperature and pressure, considerable
deviation from ideal behaviour occurs at high pressure and low temperature.
This is most easily seen by looking at Figure 6.1.2, which shows how the quantity
PV
PV
RT varies over a range of temperatures and pressures. If the gas behaved ideally, RT
would have a value of 1, regardless of the conditions.
PV
RT
Figure 6.1.2: Deviations from
ideal gas behaviour occur at high
pressures and low temperatures.
3
200 K
500 K
2
1000 K
Ideal gas
1
0
0
300
600
900
P (atm)
These variations occur because two of the assumptions used in deriving the ideal
gas equation theoretically are not justified at high pressure:
•• the size of the molecules becomes significant, compared to their separation,
when a gas is compressed
•• there is significant interaction (‘intermolecular forces’) between molecules
when a gas is compressed.
Van der Waals equations
These deviations from ideal behaviour can be corrected for by adding some extra
terms into the ideal gas equation.
This yields alternative equations of state, such as the Van der Waals equation:
[P +
an2
](V – nb) = nRT
V2
This represents the
reduction in pressure due
to the attraction between
molecules.
This represents the reduction
in ‘available volume’ due to the
space occupied by the molecules
themselves.
In this equation a and b are constants that vary for different gases; they are
evaluated experimentally and the larger the value the more deviation from ideal
behaviour will be observed.
Compressibility and the virial equation
PV
Figure 6.1.3 shows the values of RT for a range of gases at 273 K.
PV
RT is known as the compressibility factor of a gas. For an ideal gas it would have
the value 1, but for non-ideal gases it is described by the virial equation.
6.1: Chemical equilibrium and the kinetic theory of gases
5
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
For 1 mole of gas:
PV
B
C
RT = (1 + V + V2 …)
where B and C are temperature dependent coefficients that have different values
for each gas.
B
C
Figure 6.1.3: Different gases
show different levels of deviation
from ideal behaviour.
PV
RT
When V is large (as at low pressure), the terms V + V2 in the bracket become
negligible, and so the gas behaves like an ideal gas.
2.0
1.5
Ideal gas
1.0
N2
CH4
H2
CO2
0.5
0
0
200
400
600
800
1000
P (atm)
Take it further
Chemical engineers may need to use equations such as the Van der Waals or virial equations
frequently in their calculations of pressure and volume of reacting gases. Solving equations like this
is mathematically tricky and chemical engineers will have access to suitable software packages to
enable rapid solutions to be obtained.
A simplified version of one of these types of packages is available online at
http://www.webqc.org/van_der_waals_gas_law.html, enabling you to apply the Van der Waals
equation to a range of situations.
Portfolio activity (1.1, 1.2)
Hydrogen is widely used as a reactant in important industrial processes, such as the Haber process.
Along with helium, it is one of the gases whose behaviour most closely matches the behaviour of
an ideal gas.
Use ideas about ideal gas behaviour to carry out the following calculations:
1 A sample of hydrogen occupies 14 m3 at 140 K. Calculate the volume of this sample at 300 K
(assume the pressure remains constant).
2 The volume of a sample of hydrogen at 298 K is 23.6 dm3 and 1 bar pressure. The pressure is
increased to 50 bar, but the temperature is kept constant at 298 K. Calculate the new volume of
the gas.
3 Calculate the volume in dm3 of 5 moles of hydrogen gas at a temperature of 500 °C and
2 × 106 bar pressure.
In your answer:
•• state any equations you use, explaining the meaning of the terms
•• describe how the equations used to describe the behaviour of ideal gases are consistent with
the ideas of the kinetic theory of gases
•• (Distinction) discuss why hydrogen might be expected to show little deviation from ideal
behaviour under these conditions.
6.1: Chemical equilibrium and the kinetic theory of gases
6
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
2 Chemical equilibrium
Equilibrium constants
Link
This section links to Unit 5: Chemistry
for Applied Biologists, Topic guide 5.3.
Kc
From previous chemistry courses you will be aware that for any given chemical
equation, an expression for the equilibrium constant can be written, in terms of
the concentrations of the substances present in the equilibrium mixture:
aA + bB ⇌ cC + dD
(5) Kc (the equilibrium constant in terms of concentration) =
[C]c . [D]d
[A]a . [B]b
(where [A] = concentration of substance A in mol dm−3 etc.)
Kp
Key terms
Partial pressure: In a mixture of
gases, the partial pressure of a single
gas is the pressure that the gas would
exert if it was the only gas present.
Mole fraction: In a mixture of gases,
the mole fraction of a single gas is the
ratio of the number of moles of that
gas divided by the total number of
moles of gas.
For a gas phase reaction, it is more convenient to express the equilibrium constant
in terms of partial pressures.
The partial pressure of a gas, A, can be calculated from its mole fraction:
(6) XA (mole fraction of component A) =
nA
ntotal
then PA (partial pressure of component A) = Ptotal XA
so: (7) PA = Ptotal .
nA
ntotal
Then, for the equilibrium system above:
pCc . pDd
(8) Kp (the equilibrium constant in terms of partial pressures) = pa . pb
A
B
Activity
The formation of ammonia from nitrogen and hydrogen (known as the Haber process) is an
important industrial process. In one reaction vessel, equilibrium was set up at conditions of 400 °C
and 200 bar pressure.
The equation for the Haber process is: N2(g) + 3H2(g) ⇌ 2NH3 (g)
The number of moles of N2, H2 and NH3 present at equilibrium in the reaction vessel were as
follows:
N2: 1.5 mol
H2: 4.6 mol
NH3: 3.9 mol.
1
2
3
4
Calculate the mole fraction of N2, H2 and NH3.
Calculate the partial pressures of each of these gases.
Write an expression for Kp in terms of the partial pressures of N2, H2 and NH3.
Calculate a value for Kp for the reaction under the conditions specified. Give appropriate units.
6.1: Chemical equilibrium and the kinetic theory of gases
7
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
The relationship between pressure and concentration
The ideal gas law shows you how partial pressure and concentration are related:
PA = Ptotal .
Activity
Show how equation (9) can be
derived from the equations for Kp (7)
and Kc (5), along with the relationship
between pressure and concentration
(8). (Hint: Start by substituting
the expressions for PA, PB etc.
(equation (8)) into the expression for
Kp (equation (7)).)
nA
ntotal
But, from the ideal gas equation, Ptotal =
(9) So PA =
ntotalRT
Vtotal
ntotalRT nA
n
= A RT = [A] RT
Vtotal ntotal Vtotal
This also means that:
(10) Kp = KcRT−Δn
(where Δn = number of moles of product molecules in the equation − number of
moles of reactant molecules in the equation = (c+d) − (a+b)).
Kx
For a liquid phase reaction, it is more convenient to express the equilibrium
constant in terms of mole fractions:
aA(l) + bB(l) ⇌ cC(l) + dD(l)
XCc . XDd
(11) Kx (the equilibrium constant in terms of mole fractions) = Xa . Xb
Now, because from (6) PA = Ptotal . XA
A
B
(12) Kp = Kx PtotalΔn where Δn = (c+d) − (a+b)
There is a similar relationship between Kp and Kc:
(13) Kp = Kc (RT)∆n
If Kc is quoted in units of mol dm−3, then R = 0.0831 bar dm3 mol−1 K−1.
Activity
Activity
(Distinction level) Show how
equation (12) can be derived from
the expressions for Kp (8), Kx (11)
and the definition of mole fraction
(6). (Hint: Start by substituting the
expressions for PA, PB etc. (6) into the
expression for Kp (8).)
The Haber process was introduced in an earlier activity. The equation for the reaction occurring in
the Haber process is: N2(g) + 3H2(g) ⇌ 2NH3(g)
You wrote an expression for Kp in the earlier activity and calculated a value of Kp at 400 °C. In a
second reaction vessel, with a total pressure of 150 atm and a higher temperature of 450 °C, Kp has
a value of 4.9 × 10−5 bar−2.
1 Write expressions for Kc and Kx for the reaction happening in this second reaction vessel.
2 Use the value for Kp given above and equation (12) to calculate values for Kx and Kc in this
second reaction vessel (R = 0.0831 bar dm3 mol−1 K−1).
Take it further
Derivations of the interconversions between Kc, Kp and Kx are discussed in more detail online at
http://www.psci305.utep.edu/ch1305/Chapter12/gc12.pdf, which also discusses how these
expressions can be used to help interpret Le Chatelier’s principle.
6.1: Chemical equilibrium and the kinetic theory of gases
8
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Calculations using equilibrium constants
Activity
1 Hydrogen can be manufactured from steam and carbon monoxide. The equation for the
process is:
H2O(g) + CO(g) ⇌ H2(g) + CO2(g)
The Kp value for this reaction at 700 K is 8.13.
The partial pressures (in bar) of H2O, CO and CO2 in an equilibrium reached in a reaction vessel
at 700 K were: H2O: 0.72; CO: 1.21; CO2: 2.10. Calculate the partial pressure of H2.
2 Esters, used in the food industry as flavourings, are manufactured by reacting carboxylic acids
and alcohols. The equilibrium for the formation of ethyl ethanoate, CH3COOC2H5, is represented
by the equation below:
CH3COOH(l) + C2H5OH(l) ⇌ CH3COOC2H5(l) + H2O(l)
Assuming that the initial concentrations of the product molecules were both zero, what can
you say about the values of [CH3COOC2H5] and [H2O] at equilibrium?
3 In a reaction to manufacture ethyl ethanoate, the concentration of CH3COOH at equilibrium (at
a temperature of 298 K) was 0.24 mol dm−3 and that of C2H5OH was 0.58 mol dm−3. Kc for this
reaction at 298 K = 4.1.
Use this information and your answer to 2 to calculate a value for the concentration of ethyl
ethanoate at equilibrium.
Equilibrium and thermodynamic quantities
You will probably be familiar with the use of thermodynamic quantities to evaluate
the feasibility of reactions and, by extension, to make qualitative conclusions
about equilibrium positions of these reactions.
Link
Thermodynamic quantities that are used in this way include:
You can remind yourself of these
ideas in Unit 5: Chemistry for applied
biologists, Topic guide 5.2.
ΔG (Gibbs energy): The standard Gibbs energy change, ΔGƟ, is negative for any
feasible reaction.
ΔStotal (total entropy change): ΔStotal is positive for any feasible reaction.
The Gibbs energy change and equilibrium
As reaction mixtures reach equilibrium, the Gibbs energy of a mixture tends to
reach a minimum value, as shown in Figure 6.1.4.
Figure 6.1.4: Gibbs energy is a
minimum at equilibrium.
ΔGӨ reactants
ΔG° =–20 kJ mol–1
equilibrium position
favours products
100%
reactants
6.1: Chemical equilibrium and the kinetic theory of gases
Δ = GӨ products
100%
products
9
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
If the Gibbs energy of reactants and products are measured under standard
conditions, then the difference in Gibbs energy between them, as shown on the
graph in Figure 6.1.4, is simply ΔGƟ.
In this case, ΔGƟ is negative so the reaction is described as feasible. As ΔGƟ is
less negative than about −40 kJ mol−1 we would expect the reaction to reach an
equilibrium, favouring the products.
However, if we consider any point on the graph between the pure reactants
and pure products, then conditions will be non-standard. Nevertheless it is still
possible to make a conclusion about the driving force for the reaction (the value of
the Gibbs energy change) at this point in the reaction.
We can think of the reaction Gibbs energy change, ΔGr, at this point as being
represented by the slope of the graph of Gibbs energy, G, vs composition:
ΔGr =
ΔG
Δn
The different values of ΔGr are shown in Figure 6.1.5.
Figure 6.1.5: The variation in reaction
Gibbs energy with composition.
Gθ
ΔGθ
ΔGr –ve
Δn
100%
reactants
Take it further
The idea of the variation of Gibbs
energy with reaction progress is
an important and difficult idea in
thermodynamics. A fuller and stricter
explanation of its derivation can be
found in level 4/5 physical chemistry
textbooks, such as Elements of Physical
Chemistry (Atkins and de Paula, 2009),
pages 154–156.
ΔGr = 0
ΔGr +ve
100%
products
A negative value for ΔGr indicates that the reaction will tend to progress in the
forward direction and a positive value that the reaction will tend to progress in the
backwards direction.
Clearly, as Figure 6.1.5 shows, equilibrium will be reached when ΔGr = 0, since
at this point there is no driving force causing the reaction to progress in either
direction.
At this equilibrium point, ΔGr is related to both the standard Gibbs energy change,
ΔGƟ, and to the equilibrium constant K.
(14) ΔGr = ΔGƟ + RTlnK
But, since ΔGr = 0 at equilibrium,
(15) ΔGƟ = −RTlnK
R, the gas constant, has a value of 8.314 J K−1 mol−1. Notice that this means that
ΔGƟ must be expressed in units of J mol−1.
For a reaction involving gases, K is numerically equivalent to the equilibrium
constant in terms of partial pressures, Kp, although the two constants may differ in
terms of their units.
6.1: Chemical equilibrium and the kinetic theory of gases
10
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Calculating K and Kp from thermodynamic quantities
Equation (15) allows you to calculate K (and hence Kp) at given temperatures from
ΔGƟ data.
From earlier work on ΔG, you should also know how to express ΔGƟ in terms of
ΔHƟ and ΔSƟ.
(16) ΔGƟ = ΔHƟ − TΔSƟ
So, alternatively, a calculation of K could start with ΔHƟ and ΔSƟ data.
Case study
Silver(I) carbonate decomposes reversibly to form silver(I) oxide and carbon dioxide.
Ag2CO3(s) ⇌ Ag2O(s) + CO2(g)
The position of equilibrium depends on the temperature; above about 220 °C decomposition is
favoured, whereas below this temperature the reverse reaction is favoured. As a result, silver(I)
oxide is used as a reversible absorber of carbon dioxide in environments such as spacecraft – it was
used extensively in the space shuttle, for example.
ΔHƟ for this reaction = +81.6 kJ mol−1 and ΔSƟsys= +168.5 J K–1 mol−1.
1 Calculate ΔGƟ at 25 °C (298 K). Comment on the answer you get in terms of the favourability of
the process.
2 Calculate ΔGƟ at 493 K (220 °C), assuming that ΔHƟ and ΔSƟsys remain unchanged.
3 Use your answer to question 2 to calculate a value for Kp at 493 K. Comment on your answers
for ΔGƟ and Kp at this temperature.
4 Suggest how silver(I) oxide could have been used as a reversible absorber of carbon dioxide in
the space shuttle. Why is the reversibility of the process an advantage in this situation?
Activity
Lime (calcium oxide) is produced by the thermal decomposition of calcium carbonate:
CaCO3(s) ➝ CaO(s) + CO2(g)
As calcium oxide and calcium carbonate are solids, they do not appear in the Kp expression, which
therefore has the form Kp = pCO
2
The decomposition is carried out at temperatures above 1200 K, at which point ΔGƟ becomes
negative.
1 Calculate Kp at 1200 K, given that ΔGƟ at this temperature = −13.8 kJ mol−1.
2 Comment on the value of Kp at this temperature.
The effect of temperature
As you saw in the previous section, the favourability (as measured by the values of
ΔGƟ and Kp) of a process varies with temperature.
Van’t Hoff isochore
How the favourability changes depends on the sign of ΔSƟ. If it has a negative
value (because, for example, the number of moles of gas molecules increases)
then ΔGƟ will be more negative at higher temperatures and the reaction will be
more favourable.
6.1: Chemical equilibrium and the kinetic theory of gases
11
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Because ΔGƟ is in turn related to the value of the equilibrium constant, K, an
equation can be constructed showing how the value of K depends on ΔHƟ, ΔSƟ
and T.
Key term
Isochore: An equation describing an
isochoric process – i.e. one occurring
in a closed system with constant
volume.
This is known as the Van’t Hoff isochore.
(17) InK = –
ΔHƟ ΔSƟ
ΔHƟ 1 ΔSƟ
+
or InK = –
. +
RT
R
R T
R
(ΔHƟ and ΔSƟ are assumed to be constant over the temperature range being
studied.)
1
A plot of InK vs T will therefore produce a straight line with slope: –
ΔHƟ
R
ΔSƟ
The y-intercept R can also be used to derive a value for ΔSƟ (although this may
not always be easy to measure from a particular graph).
Figure 6.1.6 shows a Van’t Hoff isochore plot for the reaction:
In(Kp)
Figure 6.1.6: The Van’t Hoff
isochore suggests that a plot of
ln(Kp) vs 1/T will produce a straight
line graph, as shown here.
C(s) + CO2(g) ⇌ 2CO(g)
4
3.5
3
2.5
2
1.5
1
0.5
0
0.00084
0.00086
0.00088
0.0009
0.00092
0.00094
1/T(K-1)
Case study
Iron is produced industrially by the reduction of iron(III) oxide to iron. At the temperatures used in
the blast furnace, the reducing agent is carbon monoxide, generated by the reaction of carbon and
carbon dioxide: C(s) + CO2(g) ⇌ 2CO(g)
A plot of Kp for this process against 1/T is shown in Figure 6.1.6.
•• Calculate the gradient of this graph.
•• Use this value and equation (13) to calculate a value for ΔHƟ, in J mol−1 (R = 8.314 J K−1 mol−1).
Alternatively, this equation can be used to show how the equilibrium constants
(K1 and K2) at two different temperatures, T1 and T2, are related:
)
ΔH 1 1
Or (19) InK = InK +
R (T – T )
(18) In
(
K2 ΔHƟ 1 1
=
K1
R T1 – T2
Ɵ
2
6.1: Chemical equilibrium and the kinetic theory of gases
1
1
2
12
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Activity
Water vapour reacts with carbon to form hydrogen and carbon monoxide:
H2O(g) + C(s) ⇌ H2(g) + CO(g)
The equilibrium constant, Kp, has a value of 66 bar at 1200 K. Calculate a value for Kp at 800 K
(ΔHƟ = +145.4 kJ mol−1; assume ΔHƟ remains constant between these temperatures).
Use equation (18) or (19) to do this; let K2 represent the value of Kp at this new temperature (T2 ),
and let K1 represent the value of Kp at T1 (1200 K).
Portfolio activity (1.3, 1.4 part 1)
The Haber process is represented by the equation N2(g) + 3H2(g) ⇌ 2NH3(g)
•• Write expressions to demonstrate the meanings of the three different types of equilibrium
constant (Kp, Kc and Kx).
•• Use research to obtain values of ΔHƟ and ΔSƟ for this reaction and explain how these are used
to calculate ΔGƟ and hence the equilibrium constant K for this reaction at a given temperature.
•• Explain how Kc and Kx are related to the value for Kp for this reaction, and use the mathematical
relationships obtained to calculate values for Kc and Kx.
Portfolio activity (1.4 part 2)
The oxidation of sulfur dioxide is a critical step in the manufacture of sulfuric acid.
The reaction is represented by the equation SO2(g) + ½O2(g) ⇌ SO3(g)
Data for the equilibrium constant, Kp, (numerically equal to K) is given in Table 6.1.1.
•• Use a suitable graph and the Van’t Hoff isochore to explain how the sign and value of ΔHƟ may
be deduced from this data.
•• By using the graph or by calculation, find the value of Kp at 298 K.
Kp (bar–½)
Temperature (K)
400
397.0
500
48.1
600
9.53
700
2.63
800
0.915
900
0.384
1000
0.185
6.1: Chemical equilibrium and the kinetic theory of gases
Table 6.1.1.
13
Unit 6: Physical chemistry of spectroscopy, surfaces and chemical and phase equilibria
Checklist
At the end of this topic guide you should be familiar with the following ideas:
 the behaviour of gases is described by the ideal gas equation, pV = nRT
 deviations from ideal behaviour can occur at high pressure and low temperature and
equations exist to describe this non-ideal behaviour
 equilibrium systems are characterised by the value of the equilibrium constant at a particular
temperature
 equilibrium constants can be written in terms of concentration, partial pressures
or mole fractions
 the Gibbs energy change of a reaction is a measure of the feasibility or favourability
of a process
 Gibbs energy changes are related to equilibrium constant values by the equation
ΔG = −RTlnK
 equations can also be written which relate ΔH and/or ΔS values to equilibrium
constant values.
Further reading
Much of the content of this topic guide is covered in greater detail in level 4/5 textbooks of
physical chemistry. An excellent example is Elements of Physical Chemistry (Atkins and de Paula,
2009). This not only provides a clear background to many of the ideas encountered in the topic
guide, but also takes the concepts much further, particularly in the derivation and application of
the key mathematical equations encountered. Chapters 1, 7 and 8 are particularly relevant to this
topic guide.
For a more general (and less mathematical) treatment of the key ideas of chemical equilibrium and
Gibbs energy, Why Chemical Reactions Happen (Keeler and Wothers, 2003) is a useful resource. It is
designed as an introductory text to a level 4 chemistry course. Chapters 2 and 8 are most relevant
to this topic guide.
Acknowledgements
The publisher would like to thank the following for their kind permission to reproduce their
photographs:
Corbis: David Sutherland
All other images © Pearson Education
Every effort has been made to trace the copyright holders and we apologise in advance for any
unintentional omissions. We would be pleased to insert the appropriate acknowledgement in any
subsequent edition of this publication.
6.1: Chemical equilibrium and the kinetic theory of gases
14