Download SHM TAP1.04 MB

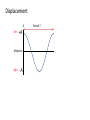
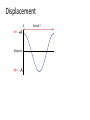
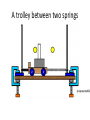
SHM TAP
Main aims
• Recognize the characteristics of SHM.
• State the condition required for SHM.
• Use equations and graphs which represent the variation of
displacement, velocity and acceleration with time.
• Investigate mass-spring systems and the simple pendulum.
• Discuss the effects of damping on SHM.
• Describe energy changes during SHM.
• State the conditions required for resonance to occur, and
its effects.
Displacement
X
left
+A
Midpoint
right
-A
Period T
Features of SHM
• An object moving with SHM oscillates either side
of a midpoint
• The distance of the object from the midpoint =
displacement
• There is always a restoring force pulling or
pushing the object back towards the midpoint
• The size of the restoring force depends on the
displacement and this force makes it accelerate
towards the midpoint
• the period is independent of the amplitude
Displacement
X
left
+A
Midpoint
right
-A
Period T
Consider …
• Where is the equilibrium position?
• Will the period of each oscillation change if
the amplitude (starting point) changes?
• How does the energy change as it oscillates?
• If there was no friction, the amplitude would
stay constant. Such oscillations (or near
constant ones) are called free oscillations.
• Does the period change as the pendulum
slows down?
• What force(s) is/are acting?
• Is it constant throughout the oscillation?
• Consider a trolley between two springs or a
mass on one spring. Would these be the
same?
• If we measure displacement from the
equilibrium position, or midpoint, sketch the
displacement – time graph for one complete
oscillation from left to right and back.
• Label +A, -A and T
+A
s = A sin t
amplitude A
A
a
0
time t
–A
periodic time T
phase changes by 2
f turns per
second
 = 2f radian
Periodic time T, frequency f, angular freque
f = 1/T unit of frequency Hz
 = 2f
Equation of sinusoidal oscillation:
s = A sin 2ft
s = A sin 
Phase dif
s = A sin 2
s = 0 when
sand falling from a swinging pendulum leaves
a trace of its motion on a moving track
s = A cos
s = A whe
t=0
• What else does the graph tell us about the motion?
• Is velocity constant throughout the oscillation? If not,
how does it accelerate?
• How can you tell that from the displacement-time
graph?
• Which way is it accelerating?
• Draw a velocity time graph on the same axis (in a
different colour)
• When is velocity zero and maximum?
• Draw an acceleration-time graph on the same axis.
When is acceleration zero/max? Compare this graph
with the displacement graph.
• What would the force-time curve look like? When is
force zero/max?
Consider your graphs with reference to the
other situations. How do they compare?
• a mass bouncing on a spring
• a trolley oscillating between two springs.
A trolley between two springs
SHM
• All clocks (starting with the pendulum in a grandfather
clock) are essentially simple harmonic oscillators
• all transmitters and receivers of waves are essentially
simple harmonic oscillators
• many aspects of engineering design from the massive to
the microscopic require a detailed knowledge of SHM (e.g.
bridges, earthquake protection of buildings, atomic force
microscopes for imaging single atoms)
• Detailed theories of the behaviour of atoms and molecules
(in solids and gases) are applications of SHM. Other aspects
of SHM are at the heart of unsolved questions in physics
today. Thus although the model oscillators that students
meet appear rather basic, they mirror pretty well
applications and problems far beyond the school laboratory
Identifying SHM
Using the apparatus of the earlier
demonstration, set one oscillator in motion.
Now change the amplitude.
What do you notice about the time period of
the oscillation?
This is a characteristic of SHM; the period is
independent of the amplitude, and we say that
the motion is isochronic.
Do these display SHM?
1. mass on a spring (vertical)
2. mass (large cube of polystyrene) on the end of a slinky
spring suspended from the ceiling
3. mass between two springs (vertical, both springs in
tension when the mass is at rest)
4. mass between two springs (horizontal, both springs in
tension when the mass is at rest – use an air track slider
for the mass to have a low friction system)
5. air track slider moving between two ‘buffer’ springs, or
rebounding due to magnetic repulsionvibrating cantilever
6. simple pendulum
7. simple ‘half’ pendulum (one that bounces off a hard
surface when its string is vertical)
1.
simple pendulum whose string intercepts a peg when vertical, so the
length of the pendulum gets shorter for one half of its cycle
2. a torsion pendulum
3. a ball bouncing off a hard surface
4. ball moving in a semi-circular shaped track (curtain rail)
5. ball moving in a vertical V shaped track (rounded enough at the point of
the V to let the ball pass easily)
6. ball moving in a vertical parabolic shaped track (draw out the parabola
on a large piece of paper to aid the bending of the track into the
parabolic shape)
7. a right circular cone on an inclined plane
8. a rectangular or square section bar balanced on top of a cylinder – the
length of the bar at right angles to the axis of the cylinder
9. water in a U tube
10. hydrometer in water
• ‘simple’ pendulum (small mass on a string)
• ‘compound’ pendulum (a rigid pendulum like a metre rule, with or
without a mass on the end)
• ‘torsion’ pendulum (a mass hanging from a single wire, executing
twisting oscillations)
• flexible strip of wood or plastic, clamped horizontally to a vertical
support, oscillating in a horizontal plane
• inertia balance (a version of the previous oscillator)
• rolling ball on curved plastic tracking
• mass oscillating on a vertical spring
• large amplitude ‘pendulum’ (vertically rotating disc, pivoted at the
centre with an off-centre mass clamped to it)
• test tube ballasted and floating vertically in water
• liquid in a large U-tube
• vehicle on an airtrack between elastic barriers
• ‘catapulting’ type oscillator (on an airtrack, or a trolley on a runway)
Study some, or all, of the following oscillating systems:
• ‘simple’ pendulum (small mass on a string)
• ‘compound’ pendulum (a rigid pendulum such as a metre rule, with
or without a mass on the end)
• ‘torsion’ pendulum (a mass hanging from a single wire, executing
twisting oscillations)
• flexible strip of wood or plastic, clamped horizontally to a vertical
support, oscillating in a horizontal plane
• inertia balance (a version of the previous oscillator)
• rolling ball on curved plastic tracking
• mass oscillating on a vertical spring
• large amplitude ‘pendulum’ (rotating disc, pivoted at the centre
with an off-centre mass clamped to it)
• test tube ballasted and floating vertically in water
• liquid in a large U-tube
• vehicle on an air track between elastic barriers
• ‘catapulting’ type oscillator (on an air track, or a trolley on a
runway).
The oscillations will fall into three
categories:
• (a) SHM (i.e. constant period) (within the
accuracy of observations)
• (b) Approximately SHM, but departing at high
amplitudes
• (c) Definitely not SHM.
It will probably emerge that (b) is the largest
category. The main point of the activity is to
demonstrate that many different oscillators behave
in a way that is simple harmonic or nearly so.
T  T0  (1 
2
16
)
• where T0 is the period for very small
amplitudes and q is the angular amplitude in
radians. For an amplitude of 1 radian (nearly
60°), T = 1.063T0, and for very lightly damped
oscillations it ought to be possible to detect
the 6% increase in period.
Observations
While you experiment on a particular oscillator consider the following
questions:
• Is the period constant (i.e. is it affected by the amplitude)? If the
motion dies away quickly, you will need to think carefully how you
will answer this point.
• Can you identify separate stiffness (k) and inertia (m) components?
If you cannot easily do this, can you pick out features of the system
that behave like k and m (and try and say in a sentence or two why
you found it difficult)?
• What adjustments do you think you would need to make to the
system to reduce its period (increase its frequency)?
Motion of harmonic oscillator
displacement
against time
large displacement to right
right
zero velocity
mass m
large force to left
left
small displacement to right
right
small velocity
to left
mass m
small force to left
left
right
large velocity
to left
mass m
zero net force
left
small displacement to left
right
small velocity
to left
mass m
left
small force to right
large displacement to left
right
zero velocity
mass m
large force to right
left
velocity
against time
force
against time
Language to describe oscillations
Sinusoidal oscillation
+A
Phasor picture
s = A sin t
amplitude A
A
angle t
0
time t
–A
periodic time T
phase changes by 2
f turns per 2 radian
second
per turn
 = 2f radian per second
Periodic time T, frequency f, angular frequency :
f = 1/T unit of frequency Hz
 = 2f
Equation of sinusoidal oscillation:
s = A sin 2ft
s = A sin t
Phase difference /2
s = A sin 2ft
s = 0 when t = 0
sand falling from a swinging pendulum leaves
a trace of its motion on a moving track
s = A cos 2ft
s = A when t = 0
t=0
Force, acceleration, velocity and displacement
Phase differences
Time traces
varies with time like:
displacement s
/2 = 90
/2 = 90
 = 180
cos 2ft
... the velocity is the rate of change
of displacement...
–sin 2ft
... the acceleration is the rate of
change of velocity...
–cos 2ft
...and the acceleration tracks the force
exactly...
–cos 2ft
velocity v
acceleration = F/m
same thing
zero
If this is how the displacement varies
with time...
force F = –ks
displacement s
... the force is exactly opposite to
the displacement...
cos 2ft
Dynamics of harmonic oscillator
How the graph starts
zero initial velocity would stay
zero if no force
velocity
force changes
velocity
How the graph continues
force of springs accelerates mass towards
centre, but less and less as the mass nears the
centre
change of velocity
decreases as
force decreases
new velocity
= initial velocity
+ change of
velocity
trace curves
inwards here
because of
inwards
change of
velocity
t
0
0
time
trace straight
here because no
change of
velocity
no force at centre:
no change of velocity
time
Uniform Circular Motion
(radius A, angular velocity )
Simple Harmonic Motion
(amplitude A, angular frequency )
Simple harmonic motion can
be visualized as the projection
of uniform circular motion onto
one axis.
The phase angle t in SHM
corresponds to the real angle
t through which the ball has
moved in circular motion.