Download Non-Euclidean Geometry

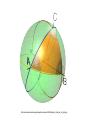
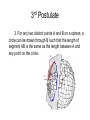
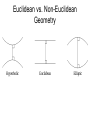
Non-Euclidean Geometry
Presented by
Daphne Hoard and Ricardo Chapa
Rice University
Mathematics Leadership Institute
July 1, 2009
Why Non-Euclidean?
Goal:
Introduce the audience to
other types of geometries
Euclidean Geometry
• Mathematical system attributed to Euclid.
• Euclid is a Greek mathematician who lived
around 300 BC.
• In the Elements, Euclid presents many
theorems deduced from a five postulates.
• It remained the only known geometry until
the 19th century.
Euclid of Alexandria
Elements
A fragment from Elements
http://scientists.penyet.net/euclid-the-father-of-geometry.html
Euclidean Geometry
Euclid’s First Four Postulates:
1. A unique straight line can be drawn
through any two points A and B
2. A segment can be extended indefinitely
3. For any two distinct points A and B, a
circle can be drawn with center A and
radius AB
4. All right angles are congruent
Euclidean Geometry
5. Given a line L and a point P not on L,
there exists a unique line though P parallel
to L.
Euclidean Geometry is Geometry in which
the parallel postulate is true.
Non-Euclidean Geometry
Throughout the centuries mathematicians
kept pondering Euclid’s parallel postulate,
refusing to accept it as an obvious truth
and trying to prove it from the first four
postulates. This ultimately gave rise to the
discovery of non-Euclidean geometries in
the 19th century.
Spherical Geometry
Spherical Geometry is geometry in which
Euclid’s fifth postulate is replaced with the
following:
Given a line G and a point P not on G, every
line through P intersects G; that is, no line
through P is parallel to G.
Spherical Geom. Terms
How do Euclidean terms, postulates, and
coordinates on the plane change in
Spherical Geometry?
A plane is the surface of a sphere.
A point is a location on the plane; however,
when we look at any two points, these
could be polar points (antipodal points).
Spherical Geom. Terms
• Polar points are the end points of the
sphere’s diameter.
• Straight lines are great circles; that is,
circles that contain any pair of polar points.
• A segment (arc segment) on a sphere is
the shortest distance between two points.
A segment is always part of a great circle,
and is also called geodesic.
Spherical Geometry
• The angle between two lines in spherical
geometry is the angle between the planes
(Euclidean) of the corresponding great
circles, and a spherical triangle is defined
by its three angles.
http://upload.wikimedia.org/wikipedia/commons/9/93/Spherical_triangle_3d_opti.png
1st & 2nd Postulates
1. Given a pair of nonpolar points A and B,
there is exactly one
line (great circle) that
contains them.
2. Any segment on a
sphere can be
extended to form a
line.
http://www.astro.uu.nl/~strous/AA/pic/Figure_4.jpg
3rd Postulate
3. For any two distinct points A and B on a sphere, a
circle can be drawn through B such that the length of
segment AB is the same as the length between A and
any point on the circle.
4th Postulate
4. All right angles are
congruent.
http://www.ugrad.physics.mcgill.ca/wiki/images/8/8c/FermiSphere1.gif
Parallel Postulate
5. Given a great circle G and a point P not
on G, every great circle through P
intersects G; that is, no great circle
through P is parallel to G
http://www.mpassociates.gr/software/distrib/science/rock/stereo_great_circles.jpg
Triangle Sum Theorem
The sum of the interior angles in
spherical triangle is greater than 180 and
less than 540 .
Interesting Facts about Spherical
Geometry
There are no rectangles in spherical
geometry.
In spherical geometry it is possible to
have a two sided polygon.
Lune
Digon
Interesting Facts about Spherical
Geometry
If A and B are not polar points, it is said that C is
between A and B if C lies on the shorter geodesic (great
circle arc) joining A and B. If A and B are antipodal, it is
said that every point is between A and B!
Longitude & Latitude
Just as Cartesian coordinates are used
to locate points in Euclid’s geometry,
Longitude and Latitude can be used on the
spherical “plane”.
The following figure illustrates
latitude lines:
http://publib.boulder.ibm.com/infocenter
The following figure illustrates
longitude lines
http://publib.boulder.ibm.com/infocenter
The following figure shows a location represented by the
coordinates longitude 80° E and latitude 55° N
http://publib.boulder.ibm.com/infocenter
http://www.worldatlas.com
Houston’s Latitude and Longitude
Houston, Tex. 29 N 95 W
http://www.infoplease.com
HYPERBOLIC GEOMETRY
HYPERBOLIC GEOMETRY
• Follows Euclid’s first four postulates:
• A unique straight line can be drawn through any two
points A and B
• A segment can be extended indefinitely
• For any two distinct points A and B, a circle can be
drawn with center A and radius AB
• All right angles are congruent
• The fifth postulate has been replaced
Hyperbolic Parallel Postulate:
• Given a line l, and a point A, not lying on
l, there exists at least two lines through A
that are parallel to line l.
Hyperbolic geometry takes place on a
curved 2-dimensional surface called
hyperbolic space.
In hyperbolic space, every point looks like a
saddle.
MODELS OF THE HYPERBOLIC
PLANE
• Upper half
• Beltrami-Klein
• Poincare Disk
POINCARE DISK
•
•
•
•
Inside of a circle
Circle not included
Edge is not a part of hyperbolic space
Disk is distorted near its edge
Terms Defined
• Geodesic- arcs of circles which meet at
the edge of the disk at 90º.
• Lines – geodesics which pass through the
center of the circle
• Polygons – a sequence of points and
geodesic segments joining those points
ANGLE MEASURES
• The measure of an angle is the radian
measure of the angle formed by
– The tangent rays at a point of intersection of
two arcs, or
– An ordinary ray and the tangent ray at a point
of intersection of the arc and the ordinary ray
TRIANGLE THEOREMS
• If two triangles are similar, they are
congruent
• All triangles have angle sums less than
180.
DEFECT OF A TRIANGLE
180 – (angle sum of triangle)
DEFECT OF A POLYGON
180(n-2) – angle sum of polygon
Finding the defect of a triangle
» Find the defect of the triangle on the left, if
its angle measures are 78º, 32º, and 43º.
» First we must find the sum of the angles of
the triangle.
» 78º+32º+43º=153º
» Next we find the defect of the angle
» Defect = 180 -153
»
= 27
AREA OF A TRIANGLE
• To find the area of a triangle in hyperbolic
space we use the formula
Area = ( π / 180 ) x defect
FIND THE AREA
Find the area of a triangle
whose angle sum is 153º.
A= π / 180 x defect
= π /180 x 27
= .471 units
IDEAL TRIANGLES
• Ideal triangles consist of 3 geodesics that
touch at the boundary of the Poincare
disk.
• The boundary of the Poincare disk is not a
part of hyperbolic space
• The sides of an ideal triangle extend
infinitely
• The sides will not intersect
• The sides of an ideal triangle get closer as
they approach the edge of the disk
• The sides of an ideal triangle are all
perpendicular to the boundary of the
Poincare disk
• They form an angle 0º with each other
Area of a Ideal Triangle
• Since all of the angles measure 0º,
the defect of the triangle is 180.
Therefore, the area of an ideal
triangle is:
• Area
=( π / 180 ) x defect
=(π / 180 ) x 180
=π
ART AND HYPERBOLIC
GEOMETRY
• M.C. Escher created four patterns using
hyperbolic geometry.
• Escher’s prints illustrates what one would
see when looking down on a hyperbolic
universe
Circle limit I
Circle Limit II
Circle Limit III
Circle Limit IV
Angels and Devils
Euclidean vs. Non-Euclidean
Geometry
NON-EUCLIDEAN GEOMETRY
• Spherical/Elliptical geometry
• Hyperbolic geometry
• Taxicab geometry
Bibliography
•
Jacobs, Harold R. Geometry. San Francisco: W.H. Freeman and Company,
1974
•
Websites
•
http://math.slu.edu/eacher/indes/php/Hyperbolic_Geometry
•
http://raider.muc.edu/MA/maendel.pdf
•
http://www.regentsprep.org/Regents/math/geometry/GGI/Euclidean.htm
•
http://members.tripod.com/~noneuclidean/hyperbolic.html
•
http://www.math.cornell.edu/~mec/Winter2009/Mihai/section5.html