Download Lecture 13 - TTU Physics

Damped Oscillators
• SHO’s: Oscillations  “Free oscillations”
because once begun, they will never stop!
• In real physical situations & for real physical
systems, of course:
– There are retarding forces: These will damp
oscillations, which eventually die away to the stop motion.
• Usual approximation: Damping force Fr  v = x
• In what fallows, take Fr = -bv, b = a constant > 0,
which depends on the system.
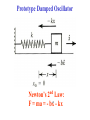
• Prototype oscillator: Mass m in 1d under combined
linear restoring force - kx + retarding force -bv.
Prototype Damped Oscillator
Newton’s 2nd Law:
F = ma = - bx - kx
• Newton’s 2nd Law Equation of Motion:
F = ma = - bv - kx
Or:
m(d2x/dt2) = - b(dx/dt) - kx
Or:
mx + bx + kx = 0
• Definitions:
– Damping Parameter: β  [b/(2m)]
– Characteristic angular frequency: ω02  (k/m)
• Equation of motion becomes:
x + 2βx + (ω0)2x = 0
• Equation of motion:
x + 2βx + ω02x = 0
• A standard, homogeneous, 2nd order differential equation.
• GENERAL SOLUTION (Appendix C!) has the form:
where
x(t) = e-βt[A1 eαt + A2 e-αt]
α  [β2 - ω02]½
A1 , A2 are determined by initial conditions: (x(0), v(0)).
[A1 eαt + A2 e-αt] can be oscillatory or exponential
depending on the relative sizes of β2 & ω02.
x(t) = e-βt[A1 eαt + A2 e-αt] with α  [β2 - ω02]½
3 cases of interest (Figure): Underdamping  ω02 > β2
Critical damping  ω02 = β2, Overdamping  ω02 < β2
x(t) (qualitative) in the 3 cases
Underdamped Case
x(t) = e-βt[A1 eαt + A2 e-αt] with α  [β2 - ω02]½
• Underdamping  ω02 > β2
• Define: ω12  ω02 - β2 > 0
ω1  “Angular frequency” of the damped oscillator.
– Strictly speaking, we can’t define a frequency when we
have damping because the motion is NOT periodic!
• The oscillator never passes twice through a given point
with the same velocity (it is slowing down!)
– However we can define: ω1 = (2π)/(2T1), T1 = time
between two adjacent crossings of x = 0
– Note: ω1 = [ω02 - β2]½ < ω0
– If the damping is small, ω1  ω0
x(t) = e-βt[A1 eαt + A2 e-αt] with α  [β2 - ω02]½
• Underdamping  ω02 > β2  ω12  ω02 - β2 > 0
– The solution is an oscillatory function multiplied by an
exponential “envelope”.
x(t) = e-βt[A1 exp(iω1t) + A2 exp(-iω1t)]
Or, defining 2 new integration constants A & δ:
x(t) = A e-βt cos(ω1t - δ)
• The oscillatory part looks just like the undamped solution with
ω02
 ω12  ω02 - β2
• The maximum amplitude of motion decreases with time by a
factor e-βt. This function forms an “envelope” function for the
oscillatory part:
xen =  A e-βt
x(t) = A e-βt cos(ω1t - δ),
xen =  A e-βt
Underdamping! Shown in fig. for δ = 0. Clearly the period is
longer (the frequency is shorter) than for the undamped case!
x(t) = A e-βt cos(ω1t - δ)
Underdamping!
• Ratio of the amplitudes at 2 successive maxima is of interest.
– Define: T  Time at which a maximum occurs.
τ1  Time between 2 successive maxima.
τ1  (2π)/ω1
– The ratio of the amplitudes at 2 successive maxima:
D  [Aexp(-βT)]/[Aexp(-β{T+ τ1})] or
D = exp(βτ1)
D  The “Decrement” of the motion
ln(D) = βτ1  “Logarithmic Decrement” of the motion
x(t) = A e-βt cos(ω1t - δ)
Underdamping!
• Consider:
v(t) = x(t) = (dx/dt) =
- β[A e-βt cos(ω1t - δ) - ω1[A e-βt sin(ω1t – δ)]
• Consider the Mechanical Energy E:
– Due to damping, E is not a constant in time! E IS NOT
CONSERVED!
– Energy is continually given up to the damping medium.
Energy dissipation in terms of heat.
E = T + U (U is due to the restoring force -kx only, not
due to the retarding force -bv).
U = U(t) = (½)k[x(t)]2, T = T(t) = (½)m[v(t)]2.
E is clearly mess! Clearly, it decays in time as e-βt
• Energy for underdamped case. See figure. (Also see Prob. 3-11)
• Energy Loss Rate in the underdamped case. See figure.
(dE/dt)  [v(t)]2 (See Prob. 3-11) (dE/dt) = is a max when
v(t) = max. (near equilibrium position). (dE/dt) = 0 when v(t) = 0
• Example 3.2: Phase Diagram - Underdamped case. Use a
computer to construct a phase diagram for the underdamped
oscillator. A = 1 cm, ω0= 1 rad/s, β = 0.2 s-1, δ = (½)π.
Define: u = ω1x, w = βx + v. Polar coordinates: ρ = [u2+w2]½
φ = ω1t. Get a logarithmic
spiral for the phase
trajectory. w vs. u:
• Phase Diagram - Underdamped case. A spiral phase path.
The continually decreasing magnitude of the radius vector is
always an indication of damped oscillations. v vs. x:
x(t) & v(t) for the case just shown