* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 13: universal gravitation
Survey
Document related concepts
Centrifugal force wikipedia , lookup
Fictitious force wikipedia , lookup
Lorentz force wikipedia , lookup
Pioneer anomaly wikipedia , lookup
Potential energy wikipedia , lookup
N-body problem wikipedia , lookup
Negative mass wikipedia , lookup
Artificial gravity wikipedia , lookup
Roche limit wikipedia , lookup
Equivalence principle wikipedia , lookup
Introduction to general relativity wikipedia , lookup
Schiehallion experiment wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Centripetal force wikipedia , lookup
Transcript
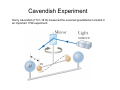
Chapter 13: universal gravitation Newton’s law of universal gravitation Newton’s law of universal gravitation: every particle in the Universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. where G ≈ 6.674×10-11 N m2 kg-2. Note that the masses are assumed to be point masses with no significant size relative to the distance the two points. The force of gravity is always an attractive force, where the gravitational force vectors of two particles are always pointed towards each other. For a spherically symmetric mass distribution, the force on a particle outside the distribution is the same as that for a point charge. Cavendish Experiment Henry Cavendish (1731–1810) measured the universal gravitational constant in an important 1798 experiment. Gravitational acceleration near the Earth’s surface The gravitational acceleration at the surface of the Earth is where and The gravitational acceleration at some height h is then . Gravitational acceleration near the Earth’s surface (cont.) For h < RE we can do a geometric expansion of the denominator about h/RE, which gives When h << RE, then Work due to universal gravitation From earlier we learned the relationship between the work due to a force and the distance If we are concerned with being outside a spherical mass, and we are interested in great distances such that the force is not approximated as a constant, and displacements along the radial direction, Work due to universal gravitation (cont.) We know that the work due to gravity is related to the potential energy, . Setting , we find In general for a small object and a mass of any distribution, the gravitational potential energy from Newton’s universal law of gravity is given by where is the mass of the small test object. Example with potential energy Potential energy of a point mass along the principal axis of the center of a ring of uniform mass density and radius R Example #2 with potential energy Potential of a point mass in a semicircle of uniform mass density Satellites in orbit - Remember that centripetal acceleration is - The magnitude of the force is which gives - Newtons law of gravity is - Determine the sum of the forces, - The only acceleration is , so A - We know the circumference of a circle and that velocity, therefore is a constant B - Find the radius of orbit by plugging in B into A and solving for radius of the orbit, . gives the Work and circular orbits How much work is done on a satellite to have it orbit 1 period? NO WORK DONE!!! and therefore Thus, Kepler's laws of planetary motion Kepler's first law: planets are orbiting the sun in a path described as an ellipse, where the sun is at one focus of the ellipse. Kepler's second law: The radius vector sweeps equal areas in equal times for a planet in motion around the sun. Kepler's third law: The period of a planet's orbit squared is proportional to its average distance from the sun cubed. The circular orbit solution for the period can be extended to an elliptical orbit by replacing the “r” by the semi-major axis “a” Gauss's law for the gravitational field Gauss's law for gravitation in integral form is The left-hand-side of the equation is the flux, flux through an arbitrary surface is defined as , through a closed surface. The In differential form, Gauss’s law for gravitation becomes