Download Ch. 1: Introduction of Mechanical Vibrations Modeling

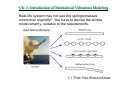
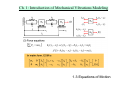
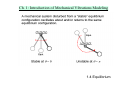
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.0 Outline
„ That You Should Know
„ Newton’s Second Law
„ Equations of Motion
„ Equilibrium, Stability
1.0 Outline
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.1 That You Should Know
Vibration is the repetitive motion of the system relative
to a stationary frame of reference or nominal position.
Principles of Motion Æ Vibration Modeling
Math Æ Vibration Analysis
*** design the system to have a particular response ***
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Spring-Mass Model
Mechanical Energy = Potential + Kinetic
From the energy point of view, vibration is caused by
the exchange of potential and kinetic energy.
When all energy goes into PE, the motion stops.
When all energy goes into KE, max velocity happens.
Spring stores potential energy by its deformation (kx2/2).
Mass stores kinetic energy by its motion (mv2/2).
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Springs and Masses connection as the way to model
the vibrating system.
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Real-life system may not see the springs/masses
connection explicitly! You have to devise the simple
model smartly, suitable to the requirements.
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Various forms of springs: linear, traverse, torsion spring
Gravity force can make up the spring!
Because work done by the gravity force is a kind of PE.
When the altitude change, PE change Æ KE change.
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Spring Æ Stiffness (N/m or Nm/rad)
Spring has the characteristic that force is the function
of deformation: F = k(x). If k is constant, the spring
is linear. Practically it is not constant. k is generally
slope of the F-x curve, and is known as the stiffness.
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Stiffness is the property of the object which depends
mainly on its shape and material properties, e.g. E.
Equivalent massless spring constants
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Equivalent massless spring constants (cont.)
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Equivalent massless spring constants (cont.)
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Equivalent massless spring constants (cont.)
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Equivalent massless spring constants (cont.)
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Spring connection: series or parallel
Forces add up
Disp. add up
The calculated stiffness value, keff, is used in the
modeling system.
keff
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 1
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 2
Derive the equivalent spring constant for the system
in the figure.
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
let the system be deviated by torque τ
F
at that point
k=
Δ
at distance l = a, Feq =
at distance l = b, Feq =
τ
a
and Δ =δ ⇒ kl = a =
τ
b
and Δ = δ ⇒ kl =b
b
a
τ
aδ
τa
= 2 = k2
bδ
k 2b 2
τ k2b 2
=
∴ kl = a = 2
δ
a
a
kl = a
k1k2b 2
=
is in series with k1 ∴ keq =
1 k1a 2 + k2b 2
1
+
kl = a k1
1
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Perturb the system by force F and observe the displacement x
F
keq =
but F = k1 ( x − aθ )
x
k ( x − aθ )
∴ keq = 1
⇒ need to find relation between x and θ
x
⎡⎣ ∑ M O = 0 ⎤⎦ k2bθ × b − k1 ( x − aθ ) × a = 0
k1ax
k1k2b 2
θ= 2
∴ keq =
2
k1a + k2b
k1a 2 + k2b 2
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 3
The system shown in the figure consists of two gears A
and B mounted on uniform circular shafts of equal
Stiffness GJ/L; the gears are capable of rolling on
each other without slip. Derive an expression for the
Equivalent spring constant of the system for the
radii ratio Ra / Rb = n.
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Apply torque M at gear A, then gear A rotates θ A .
Shaft exerts resistant moment M A and gear B exerts reaction force F .
In turns, at gear B, opposite reaction force − F happens and
shaft exerts moment M B to resist rotation θ B .
keq@A =
M
θA
⇒ need to write M and θ A as functions of given parameters.
⎡⎣ ∑ M = 0 ⎤⎦ M = M A + FRA and M B = FRB
GJ
GJ
by spring stiffness, M A =
θ A and M B =
θB
L
L
θ
R
by geometry, n = A = B
RB θ A
GJ
θB
GJ
GJ
L
θA +
∴M =
RA =
1 + n2 )θA
(
RB
L
L
∴ keq@A =
M
θA
=
GJ
1 + n2 )
(
L
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
θB ⎛ M A ⎞
=⎜
⎟ =n
θ A ⎝ M B ⎠ trans
torsional spring at gear B is connected to gear A
M
GJ 1 M A
kB = B =
= 2
⇒ gear A sees stiffness at gear B = n 2 kB
L
n θA
θB
∵ springs are connected in parallel, equivalent stiffness at gear A
GJ
keq@A = kA + n 2 kB =
1 + n2 )
(
L
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 4
The two gears of the system have mass polar moment
of inertia IA and IB. Derive an expression for the
equivalent mass polar moment of inertia for the radii
ratio RA / RB = n.
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ignore the torsional spring and write the equation of motion at gear A
⎡⎣ ∑ M = Iθ ⎤⎦ M − FRA = I Aθ A
to eliminate F , consider motion at gear B
FRB = I Bθ B
Employ the geometric constraints:
θB
R
=n= A
θA
RB
I B n 2θ A
RA = I Aθ A ⇒ M = ( I A + n 2 I B )θ A
M−
RA
∴ I eq@A = I A + n 2 I B
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Mass, Inertia
To store / release kinetic energy
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
Damper Æ viscous coefficient (Ns/m or Nms/rad)
To dissipate energy
f d = − F = −cx
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.1 That You Should Know
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.2 Newton’s Second Law
Many ways to derive the equations of motions
Newton-Euler is one, which is suitable for situations…
• system in planar motion
• force and motion have constant direction
• system is simple
1.2 Newton’s Second Law
Ch. 1: Introduction of Mechanical Vibrations Modeling
Relative Velocity
v A = v B + ω × rA/B + v rel
v A = velocity of the particle A
v B = velocity of the particle B
v A/B = velocity of A relative to B
= ω × rA/B + v rel ≠ velocity of A as seen from the observer
v rel = xi + yj
= velocity of A as seen from an observer
at anywhere fixed to the rotating x-y axes
ω × rA/B = ( v rel observed from nonrotating x-y )
− ( v rel observed from rotating x-y )
If we use nonrotating axes, there will be no ω × rA/B term.
This makes v rel = v A/B , which means the velocity seen by
the observer is the velocity of A relative to B.
If B coincides with A, rA/B = 0. This makes v rel = v A/B ,
which means the velocity seen by the observer is the
velocity of A relative to B, even the observer is rotating.
1.2 Newton’s Second Law
Ch. 1: Introduction of Mechanical Vibrations Modeling
Relative Acceleration
Differentiating the relative velocity equation results in
the relative acceleration equation:
a A = a B + ω × rA/B + ω × rA/B + v rel
V
Recall the vector differentiation relation,
rA/B = v rel + ω × rA/B
ω
v rel = a rel + ω × v rel
⎛ dω ⎞
⎛ dω ⎞
⎛ dω ⎞
,
+
ω
×
ω
∴
=
⎟
⎜
⎟
⎜
⎟
⎝ dt ⎠ xy
⎝ dt ⎠XY ⎝ dt ⎠ xy
ω =⎜
→ angular acceleration observed in fixed frame = that observed in the rotating frame
Note: rA/B = xi + yj v rel = xi + yj a rel = xi + yj
( v rel
and a rel = velocity and acceleration seen by the rotating observer )
∴ a A = a B + ω × rA/B + ω × (ω × rA/B ) + 2ω × v rel + a rel
1.2 Newton’s Second Law
Ch. 1: Introduction of Mechanical Vibrations Modeling
Newton formula for translational motion of the rigid body
∑ F = ma
G
∑F =
the resultant of the external forces
= forces applied to the rigid body
m = total mass
aG = the acceleration of the center of mass G
FBD
1.2 Newton’s Second Law
Ch. 1: Introduction of Mechanical Vibrations Modeling
Euler formula for planar rotational motion of the rigid
body
∑M
Gz
= I Gω
∑M
Gz
= moment of the external forces about CM (G) in z − direction
I G = centroidal mass moment of inertia about z − axis through CM (G)
ω = rate of change of the angular velocity
FBD
1.2 Newton’s Second Law
Ch. 1: Introduction of Mechanical Vibrations Modeling
Pure rotation Æ stationary point in the body
∑M
Oz
= I Oω
∑M
Gz
= moment of the external forces about O in z − direction
I O = mass moment of inertia about z − axis through axis of rotation (O)
ω = rate of change of the angular velocity
I O = I G + md 2
FBD
With this formula, the constraint force is eliminated
1.2 Newton’s Second Law
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 5 Simple 1 DOF m-k system
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 6 Simple 2 DOF m-k system
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 7 Simple 1 DOF pendulum
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 8 Compound 2 DOF pendulum
A uniform rigid bar of total mass m and length L2,
suspended at point O by a string of length L1, is acted
upon by the horizontal force F. Use the angular
displacement θ1 and θ2 to define the position, velocity,
and acceleration of the mass center C in terms of
body axes and then derive the EOM for the translation
of C and the rotation about C.
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
L
⎡
⎤
F s θ 2 + mg c θ 2 − T c θ 2−1 = m ⎢ L1θ1 s θ 2−1 − L1θ12 c θ 2−1 − 2 θ 22 ⎥
2 ⎦
⎣
L ⎤
⎡
Fcθ 2 − mgsθ 2 + Tsθ 2−1 = m ⎢ L1θ1cθ 2−1 + L1θ12sθ 2−1 + 2 θ 2 ⎥
2 ⎦
⎣
L2
L2
mL22
θ2
F c θ 2 − T s θ 2−1 =
2
2
12
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
eliminate the constraint force T
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 9 Washing machine
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 9 Washing machine
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
y measured from unstrained spring position
My + cy + ky = − Mg
x measured from static equilibrium position
static displacement equilibrium δ st = Mg / k
y = x − δ st
Mx + cx + kx = 0 Weight is balanced at all times by spring force kδ st
Imbalance in the washer
Mx + cx + kx = F = meω 2 sin ωt
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 10 Pitch & Vertical motion simple model of a car
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
(
F − ksf ( xb − aθ − x f ) − csf xb − aθ − x f
)
(
)
Fc + ⎡⎣ k ( x − aθ − x ) + c ( x − aθ − x ) ⎤⎦ a
− ⎡⎣ k ( x + bθ − x ) + c ( x + bθ − x ) ⎤⎦ b = I θ
k ( x − aθ − x ) + c ( x − aθ − x ) − k x = m x
k ( x + bθ − x ) + c ( x + bθ − x ) − k x = m x
−k sr ( xb + bθ − xr ) − csr xb + bθ − xr = mb xb
sf
sr
b
f
b
r
sf
sr
sf
b
f
sf
sr
b
r
sr
b
f
b
r
b
b
f
r
C
f
r r
f
f
f
r r
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
−csf a + csr b −csf
0 ⎤ ⎡ xb ⎤ ⎡ csf + csr
IC 0
0 ⎥⎥ ⎢⎢ θ ⎥⎥ ⎢⎢ −csf a + csr b csf a 2 + csr b 2 csf a
+
⎢ −csf
⎥
⎢
⎥
csf a
csf
0 mf 0 xf
⎥⎢ ⎥ ⎢
0
−csr b
0
0 mr ⎦ ⎣ xr ⎦ ⎣ −csr
−k sf a + k sr b − ksf −k sr ⎤ ⎡ xb ⎤ ⎡ F ⎤
⎡ k sf + k sr
⎢ − k a + k b k a 2 + k b 2 k a − k b ⎥ ⎢ θ ⎥ ⎢ Fc ⎥
sr
sf
sr
sf
sr ⎥ ⎢
⎥=⎢ ⎥
+ ⎢ sf
⎢ −ksf
k sf a
k sf
0 ⎥ ⎢xf ⎥ ⎢ 0 ⎥
⎢
⎥⎢ ⎥ ⎢ ⎥
−
−
k
k
b
k
0
⎣0⎦
sr
sr
sr ⎦ ⎣ xr ⎦
⎣
⎡ mb
⎢0
⎢
⎢0
⎢
⎣0
0
0
−csr ⎤ ⎡ xb ⎤
−csr b ⎥⎥ ⎢⎢ θ ⎥⎥
0 ⎥ ⎢xf ⎥
⎥⎢ ⎥
csr ⎦ ⎣ xr ⎦
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 11 EOM w/ springs in series
A mass m is suspended on a massless beam of uniform
flexural rigidity EI. Derive the differential EOM.
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
192 EI
L3
From the arrangement, it is connected in series with the spring k
equivalent stiffness of the beam at the midspan is
192kEI
192 EI + kL3
192kEI
x=0
∴ mx +
192 EI + kL3
∴ keq =
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 12 EOM w/ springs in parallel
Devise a lumped model for the n-storey building
subjected to a horizontal earthquake excitation.
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
xi +1 > xi > xi −1
ki ( xi − xi −1 )
ki +1 ( xi +1 − xi )
xi > xi +1 and xi > xi −1
ki ( xi − xi −1 )
ki +1 ( xi − xi +1 )
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
Each column acts as clamped-clamped beam
12 EI
.
H3
Two columns for each storey behave like spring in parallel.
24 EI i
∴ keqi =
H i3
with an end in horizontal deflection ⇒ k =
Schematic model is a string of spring/mass.
At each mass
⎡⎣ ∑ F = ma ⎤⎦ mi xi = ki +1 ( xi +1 − xi ) − ki ( xi − xi −1 ) , xi +1 > xi > xi −1
or
⎡⎣ ∑ F = ma ⎤⎦ mi xi = − ki +1 ( xi − xi +1 ) − ki ( xi − xi −1 ) , xi > xi +1 and xi > xi −1
t t
with the constraint xo ( t ) = xo ( 0 ) + ∫ ∫ a ( t ) dt
0 0
1.3 Equations of Motion
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.4 Equilibrium and Linearization
Linear Time Invariant (LTI) system is convenient to
understand and analyzed. It can be described as the
system of ordinary differential equations with constant
coefficients of the form:
dmx
d m −1 x
d 2x
dx
+ ami x = f ( t )
a0i m + a1i m −1 + … + a( m − 2)i 2 + a( m −1)i
dt
dt
dt
dt
Very often, the EOM is nonlinear which is difficult to
manipulate. Linearization makes the system become
LTI using the Taylor’s series expansion around an
interested point. The equilibrium point is commonly
chosen.
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
How to find the equilibrium point?
The solution does not change if the system is at the
equilibrium. Let that point be x = xe and at that point
x = x = … = 0. Substitute into EOM and solve for xe .
How to linearize the model?
Apply the Taylor’s series expansion to any nonlinear
expressions around xe . Assume small motion, which
allows one to ignore the nonlinear terms in the series.
In other words, only the constant and linear terms are
remained.
d
1 d2
2
−
+…
f ( x ) = f ( xe ) +
f ( x)
f
x
x
x
( x − xe ) +
(
)
(
)
e
2
2! dx
dx
x = xe
x= x
e
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 13 Inverted pendulum
Determine the EOM and linearize it.
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
l
l
⎡⎣ ∑ M O = I Oα ⎤⎦ − 2k sθ × cθ + mglsθ = ml 2θ
2
2
Find the equilibrium position θ = θ e
kl 2
2mg
sθ e cθ e + mglsθ e = 0, sθ e = 0 or cθ e =
−
kl
2
Linearize about θ e = 0 for which θ = θ e + φ
mg
⎛ kl 2
⎞
l
l
−2k sθ × cθ + mglsθ = 0 + ⎜ −
+ mgl ⎟ φ
2
2
⎝ 2
⎠
2k(l/2)sθ
(l/2)cθ
⎛ kl 2
⎞
∴ ml φ + ⎜
− mgl ⎟ φ = 0, φ measured from θ = 0
⎝ 2
⎠
2
2mg
4m 2 g 2
Linearize about θ e such that cθ e =
, sθ e = 1 − 2 2 for which θ = θ e + φ
kl
k l
⎛ kl 2 6m 2 g 2 ⎞
l
l
−2k sθ × cθ + mglsθ = 0 + ⎜ −
+
⎟φ
2
2
2
k
⎝
⎠
⎛ kl 2 6m 2 g 2 ⎞
−1 ⎛ 2mg ⎞
∴ ml φ + ⎜
−
⎟ φ = 0, φ measured from θ = cos ⎜
⎟
k ⎠
⎝ kl ⎠
⎝ 2
2
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
l
l
⎡⎣ ∑ M O = I Oα ⎤⎦ − 2k θ × + mglθ = ml 2θ
2
2
⎛ kl 2
⎞
∴ ml θ + ⎜
− mgl ⎟ θ = 0
⎝ 2
⎠
2
mg
2k(l/2)θ
(l/2)
small angle approx.
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 14
Determine the EOM and linearize it.
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
kl1θ
mg
small angle approx.
⎡⎣ ∑ M O = I Oα ⎤⎦ − mgl2θ − kl1θ × l1 = ml 2θ
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
Ex. 15
Determine the EOM and linearize it.
equilibrium position
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
Let the equilibrium position the spring deforms by δ eq .
⎡⎣ ∑ Fy = 0 ⎤⎦ mg − kδ eq cα = 0 _____________________ (1)
Let y be the displacement measured from the equilibrium,
corresponding to the spring being deflected by angle θ .
⎡⎣ ∑ Fy = my ⎤⎦ mg − cy − k ( Δ + δ eq ) c (α − θ ) = my ____ ( 2 )
From the geometry, Δ is the difference of the spring length
between two postures.
Δ=
( h tan α ) + ( h + y )
2
2
h
h2
h
−
= 2 + 2hy + y 2 −
cα
cα
cα
From the geometry,
h
h+ y
h tan α
sα =
s (α − θ ) ⇒ tan (α − θ ) =
cα
c (α − θ )
h+ y
⎡ 2
⎤
1
=
β
c
c (α − θ ) =
⎢
⎥
2
1 + tan β ⎦
⎣
h+ y
h2
+ 2hy + y 2
2
cα
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
Subs. the findings into ( 2 ) and recognize (1) :
⎛ h2
⎞
h
+ δ eq ⎟
mg − cy − k ⎜ 2 + 2hy + y 2 −
⎜ cα
⎟
cα
⎝
⎠
EOM: my + cy + k ( h + y ) −
h+ y
2
= my
h
+ 2hy + y 2
2
cα
h+ y
mg
= mg −
cα
h2
2
2
+
+
hy
y
c 2α
kh
cα
I
h+ y
h2
2
2
+
+
hy
y
c 2α
II
Linearization about equilibrium y = 0
⎧
⎪
⎪
2
⎪⎪
kh
kh
I = kh −
+ ⎨k −
h ⎪ cα
cα
cα ⎪
⎪
⎪⎩
( h + y )( 2h + 2 y )
h2
2
+
2
hy
+
y
−
c 2α
h2
2 2 + 2hy + y 2
cα
2
h
+ 2hy + y 2
2
cα
⎫
⎪
⎪
⎪⎪
2
⎬ ( y − 0) + O ( y )
⎪
⎪
⎪
⎪⎭ y =0
I ≈ kc 2α ⋅ y
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
⎧ h2
( h + y )( 2h + 2 y )
2
⎪ 2 + 2hy + y −
h2
⎪ cα
2
2
2
+
+
hy
y
2
mgh mg ⎪⎪
cα
II = mg −
−
⎨
h cα ⎪
h2
cα
+ 2hy + y 2
2
cα
⎪
cα
⎪
⎪⎩
⎫
⎪
⎪
⎪⎪
2
⎬ ( y − 0) + O ( y )
⎪
⎪
⎪
⎪⎭ y =0
mg 2
s α⋅y
h
Subs. I and II into EOM,
II ≈
mg 2 ⎞
⎛
my + cy + ⎜ kc 2α −
s α⎟y=0
h
⎝
⎠
If α − θ ≈ α , i.e. θ is very small, which requires small enough α , then ( 2 ) becomes
mg − cy − k ( Δ + δ eq ) cα = my
Make use of (1) , it becomes my + cy + k Δcα = 0
Subs. Δ and linearize about y = 0 to get
my + cy + kc 2α ⋅ y = 0
Note that the linearized Δ = ycα which makes sense from the figure
by projecting y onto the line of spring.
1.4 Equilibrium
Ch. 1: Introduction of Mechanical Vibrations Modeling
1.4 Equilibrium