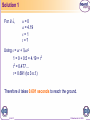Download Connected Particles

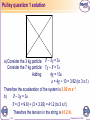
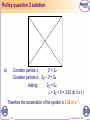
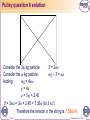
AS-Level Maths:
Mechanics 1
for Edexcel
M1.5 Dynamics 2
These icons indicate that teacher’s notes or useful web addresses are available in the Notes Page.
This icon indicates the slide contains activities created in Flash. These activities are not editable.
For more detailed instructions, see the Getting Started presentation.
11 of
of 67
67
© Boardworks Ltd 2005
Contents
Pulleys
Pulleys
Internal and external forces
Towing
Friction on a moving particle
Examination style questions
22 of
of 67
67
© Boardworks Ltd 2005
Connected particles
We talk about connected particles when we are considering
situations where two objects are joined together.
There are two types of situations that involve connected
particles.
1. In the first situation, two masses are connected by a
string which passes over a pulley.
2. In the second situation, is one mass tows another;
for example, a car towing a caravan or a train
engine pulling a carriage.
3 of 67
© Boardworks Ltd 2005
Pulleys
This example
shows how to find
the acceleration
of connected
masses passing
over a pulley.
Applying Newton’s second law:
m1g – T = m1a
T – m2g = m2a
Adding:
4 of 67
T = tension in Newtons
a = acceleration
m = mass
Force = mass × acceleration
F = ma
m1g – m2g = m1a + m2a
m1  m2
a 
g
m1  m2
© Boardworks Ltd 2005
Pulleys
This example shows
how to find the
acceleration of
connected masses
passing over a pulley,
when the masses are
not acting vertically.
Applying Newton’s second law:
m2g – T = m2a
T – m1gcos(90 – ) = m1a
Adding:
m2g – m1gsin = m1a + m2a
a 
5 of 67
90 – θ is the angle
between the direction of
the force, and the vertical.
m2  m1 sin
m1  m2
g
© Boardworks Ltd 2005
Pulley question 1
Particles of mass 3 kg and 7 kg are attached to each end of
a light inextensible string which passes over a smooth fixed
pulley.
The system is released from rest.
a) Find the acceleration of the system.
b) Find the tension in the string.
6 of 67
© Boardworks Ltd 2005
Pulley question 1 solution
a) Consider the 3 kg particle: T – 3g = 3a
Consider the 7 kg particle: 7g – T = 7a
Adding:
4g = 10a
a = 4g ÷ 10 = 3.92 (to 3 s.f.)
Therefore the acceleration of the system is 3.92 m s–2.
b)
T – 3g = 3a
T = (3 × 9.8) + (3 × 3.92) = 41.2 (to 3 s.f.)
Therefore the tension in the string is 41.2 N.
7 of 67
© Boardworks Ltd 2005
Pulley question 2
A particle A of mass 3 kg is resting on a smooth,
horizontal table top, which is 2 m above the floor. This
particle is connected to a particle B of mass 2 kg by a
light inextensible string which hangs freely over a smooth
fixed pulley at the edge of the table.
Particle A is held at rest at a point 1 m from the pulley.
The system is then released from rest.
a) Find the acceleration of the system before A
reaches the pulley.
b) Find the time taken for A to reach the pulley.
8 of 67
© Boardworks Ltd 2005
Pulley question 2 solution
a)
Consider particle A:
T = 3a
Consider particle B: 2g – T = 2a
Adding:
2g = 5a
a = 2g ÷ 5 = 3.92 (to 3 s.f.)
Therefore the acceleration of the system is 3.92 m s–2.
9 of 67
© Boardworks Ltd 2005
Pulley question 2 solution cont.
b) Consider particle A:
distance (m)
initial velocity (m s–1)
acceleration (m s–2)
time (sec)
s=1
u=0
a = 3.92
t is unknown
Constant acceleration formula
Using s = ut + ½at2:
1 = 0 + 1.96t2
t = 0.714 (to 3 s.f.)
It takes 0.714 seconds for particle A to reach the pulley.
10 of 67
© Boardworks Ltd 2005
Pulley question 3
A particle A of mass 4 kg is resting on a rough plane
inclined at an angle of 30° to the horizontal. The particle is
connected by a light inextensible string to a particle B of
mass 6 kg, which hangs freely over a smooth fixed pulley
at the top of the inclined plane.
The coefficient of friction between the particle and the
plane is 0.15.
The system is released from rest.
Find the acceleration of the system.
11 of 67
© Boardworks Ltd 2005
Pulley question 3 solution
Resolve perpendicular to the plane:
R = 4gcos30° = 33.9 (to 3 s.f.)
F = R = 0.15 × 33.9 = 5.09 (to 3 s.f.)
Consider particle A: T – 5.09 – 4gcos60° = 4a
Consider particle B: 6g – T = 6a
Adding:
6g – 5.09 – 4gcos60° = 10a
1
a=
(6g – 5.09 – 4gcos60°) = 3.41 (to 3 s.f.)
10
Therefore the acceleration of the system is 3.41 m s–2.
12 of 67
© Boardworks Ltd 2005
Pulley question 4
Example 4: A particle A of mass 3 kg is resting on a sloping
surface. It is connected to another particle B of mass 5 kg,
which hangs freely by a light inextensible string that passes
over a smooth pulley at the bottom of the slope.
The sloping surface is assumed to be smooth and is inclined
at an angle of 20° to the horizontal.
Find the acceleration when the system is released
from rest.
13 of 67
© Boardworks Ltd 2005
Pulley question 4 solution
In this example, gravity and the
tension in the string are pulling
particle A in the same direction.
Consider particle A:
Consider particle B:
Adding:
T + 3gcos70° = 3a
5g – T = 5a
5g + 3gcos70° = 8a
1
a = (5g + 3gcos70°)
8
Therefore the acceleration of the system is 7.38 m s–2.
14 of 67
© Boardworks Ltd 2005
Pulley question 5
Example 5: Two particles of mass 2 kg and 5 kg are
resting either side of a rough inclined slope. The side that
the 2 kg particle rests on is inclined at an angle of 25° to
the horizontal and the other side is inclined at an angle of
30° to the horizontal.
The coefficients of friction between the particles and the
surface of each side of the slope are equal.
The acceleration when the system is released from rest is
2 m s–2.
a) Find the coefficient of friction between the particles
and the slope.
b) Find the tension in the string.
15 of 67
© Boardworks Ltd 2005
Pulley question 5 Solution
a) Resolve perpendicular to the plane:
Resolve perpendicular to the plane:
Consider the 2 kg particle:
T – 2gcos65° – F1 = 2 × 2
T – 2gcos65° – 2gcos25° = 4
Consider the 5 kg particle:
5gcos60° – F2 – T = 5 × 2
5gcos60° – 5gcos30° – T = 10
16 of 67
R1 = 2gcos25°
R2 = 5gcos30°
mass × acceleration
Remember, F = R
© Boardworks Ltd 2005
Pulley question 5 solution
Adding: 5gcos60° – 5gcos30° – 2gcos65° – 2gcos25° = 14
5gcos30° + 2gcos25° = 5gcos60° – 2gcos65° – 14
Therefore,  
5 gcos60° – 2 gcos65° – 14
 0.0368 (to 3 s.f.)
5 gcos30°  2 gcos25°
b) Consider the 2 kg particle: T – 2gcos65° – 2gcos25° = 4
Therefore, T = 2gcos65° + 4 + 2gcos25° × 0.0368
T = 12.9 (to 3 s.f.)
The tension in the string is 12.9 N.
17 of 67
© Boardworks Ltd 2005
Pulley question 6
Example 6: Two particles A and B are connected by a light
inextensible string which passes over a smooth peg. Particle
A has mass 3m kg and is resting on a smooth horizontal
table. Particle B of mass m kg is hanging freely over the peg
which is positioned on the edge of the table.
The system is released from rest.
Find the tension in the string in terms of m.
18 of 67
© Boardworks Ltd 2005
Pulley question 6 solution
Consider the 3m kg particle:
T = 3ma
Consider the m kg particle:
mg – T = ma
Adding:
mg = 4ma
g = 4a
a = ¼g = 2.45
T = 3ma = 3m × 2.45 = 7.35m (to 3 s.f.)
Therefore the tension in the string is 7.35m N.
19 of 67
© Boardworks Ltd 2005
Contents
Pulleys
Pulleys
Internal and external forces
Towing
Friction on a moving particle
Examination style questions
20
20 of
of 67
67
© Boardworks Ltd 2005
Internal and external forces
Whether a force is internal or external has nothing to do with
the force itself, but rather the system under consideration.
So, whether a force is internal or external is not an intrinsic
property of the force.
The next two examples illustrate the distinction between
internal and external forces.
21 of 67
© Boardworks Ltd 2005
Towing example
Example: A car of mass m1 pulls a trailer of mass m2 along a
straight horizontal road. The resistance to the motion of the
car is F1 and the resistance to the motion of the trailer is F2.
The engine of the car produces a driving force of magnitude
R.
Find, in terms of m1, m2, F1, F2 and R,
a) The acceleration of the system.
b) The tension in the coupling between the car and the
trailer.
22 of 67
© Boardworks Ltd 2005
Towing example solution
a) When considering the motion of the car and trailer as a
single entity, the tension in the coupling is an internal
force and does not appear on the diagram.
Applying Newton’s second law:
R – F1 – F2 = (m1 + m2)a
a 
R  F1  F2
m  m2
1
23 of 67
© Boardworks Ltd 2005
Towing example solution
In order to calculate the tension in the coupling, the motion of
the car and trailer must be considered separately. In this
system, the tension is now an external force. The tension can
be calculated by looking at either the motion of the car or the
trailer. You could use the unused method to check the answer.
Forces acting on the trailer:
T is now an external force and must appear on the diagram.
24 of 67
© Boardworks Ltd 2005
Towing example solution
Applying Newton’s second law:
T – F2 = m2a
Substituting in
 T = F2 + m2a
answer to part a).
R  F1  F2
T  F2  m2
m1  m2
m F m F m Rm F m F
2 2
2
2 1
2 2
T 1 2
m m
1
T
25 of 67
m F m Rm F
1 2
2
m m
1
2
2
2 2
© Boardworks Ltd 2005
Towing example solution
Forces acting on the car:
Applying Newton’s second law:
R – T – F1 = m1a

T = R – F1 – m1a
R  F1  F2
T  R  F  m1
1
m1  m2
m R  m R  m F  m F  m1R  m1F1  m1F2
2
1 1
2 2
T 1
m m
1
2
m F m Rm F
2
2 2
T 1 2
m m
1
26 of 67
2
© Boardworks Ltd 2005
Lift example
Example: A man of mass m1 is travelling upwards in a lift of
mass m2 which has constant acceleration a. The tension in
the cable of the lift is T.
Find in terms of m1, m2, g and T,
a) The acceleration of the lift.
b) The normal contact force, R, between the man
and the floor of the lift.
27 of 67
© Boardworks Ltd 2005
Lift example solution
When considering the motion of the man and the lift together
the normal contact force is an internal force and does not
appear on the diagram.
a) Applying Newton’s second law:
T – m1g – m2g = (m1 + m2)a
a 
28 of 67
T  m1g  m2 g
m1  m2
© Boardworks Ltd 2005
Lift example solution
In order to calculate the normal contact force between the man
and the floor of the lift, the motion of the man and the lift must
be considered separately. The normal contact force can be
calculated by looking at either the man or the lift. You could
use the unused method to check the answer.
b) Forces acting on the man:
R is now an external force
and must appear on the
diagram.
29 of 67
© Boardworks Ltd 2005
Lift example solution
Applying Newton’s second law:
R – m1g = m1a
R = m1a + m1g
Substituting in
answer to part a).
R  m1
R
R
30 of 67
T  m1g  m2 g
m1  m2
 m1g
m1T  m12 g  m1m2 g  m12 g  m1m2 g
m1  m2
m1T
m1  m2
© Boardworks Ltd 2005
Lift example solution
Forces acting on the lift:
Newton’s third law dictates that
the force that the man exerts on
the floor of the lift is equal and
opposite to the force on the man.
Applying Newton’s second law:
T – N – m2g = m2a
N = T – m2g – m2a
N T m g m
2
N
N
31 of 67
2
So, N = R
T  m1g  m2 g
m1  m2
m1T  m T  m1m2 g  m22 g  m T  m1m2 g  m 2 g
2
m1T
m1  m2
m1  m2
2
2
© Boardworks Ltd 2005
Contents
Pulleys
Pulleys
Internal and external forces
Towing
Friction on a moving particle
Examination style questions
32
32 of
of 67
67
© Boardworks Ltd 2005
Towing question 1
A car is pulling a caravan along a straight horizontal road.
The mass of the car is 1200 kg and the mass of the caravan
is 900 kg.
The car and caravan are subject to resistive forces of 600 N
and 550 N respectively.
There is a constant driving force of 2200 N acting on the car.
a) Find the magnitude of the acceleration of the car
and caravan.
b) Find the tension in the towbar.
33 of 67
© Boardworks Ltd 2005
Towing question solution
a) Applying Newton’s second law to the whole system:
2200 – 600 – 550 = (900 + 1200) × a
2100a = 1050
a = 0.5
Therefore the acceleration of the car
and caravan is 0.5 m s–2.
34 of 67
© Boardworks Ltd 2005
Towing question solution
b) Applying Newton’s second Law to the car only,
2200 – 600 – T = 1200 × 0.5
T = 2200 – 600 – 600
T = 1000
Therefore the tension in the towbar is 1000 N.
35 of 67
© Boardworks Ltd 2005
Towing question 2
A train comprises an engine of mass 40,000 kg coupled to two
trucks, each of mass 8000 kg. The train moves along a
horizontal road. The resistances to the motion of the engine,
middle truck and last truck are 15,000 N, 5000 N and 2000 N
respectively. The tension in the coupling between the two
trucks is 0.
a) Show that the train is decelerating and find the
magnitude of this deceleration.
b) Find the tension in the coupling between the engine
and the middle truck.
c) Determine whether the engine is exerting a braking or
driving force, and find the magnitude of this force.
36 of 67
© Boardworks Ltd 2005
Towing question solution
a) Applying Newton’s second law to the last truck:
0 – 2000 = 8000a
–2000
a=
= –0.25
8000
Therefore the train is decelerating at a rate of 0.25 m s–2.
37 of 67
© Boardworks Ltd 2005
Towing question solution
b) Applying Newton’s second law to the middle truck:
T – 5000 = 8000 × –0.25
T = 5000 – 2000
T = 3000
Therefore the tension in the towbar is 3000 N.
38 of 67
© Boardworks Ltd 2005
Towing question solution
Use F = ma on the whole train:
E – 15,000 – 5000 – 2000 = 56,000 × –0.25
E = 15,000 + 5000 + 2000 – 14,000
E = 8000
Therefore the engine is exerting a driving force of 8000 N.
39 of 67
© Boardworks Ltd 2005
Contents
Pulleys
Pulleys
Internal and external forces
Towing
Friction on a moving particle
Examination style questions
40
40 of
of 67
67
© Boardworks Ltd 2005
The coefficient of friction
Friction is a very common force that acts on objects moving
relative to each other (for example a block sliding along a
table) to eventually slow them down.
Many of the examples involving moving objects have
involved a resistive force. This is often due to friction.
Friction depends on the roughness of the bodies touching
and on the normal contact force. The roughness is
characterised by the coefficient of friction, μ, and the
frictional force is then F = μR.
As μ gets closer to 1, the rougher the contact between the
surfaces. As μ gets closer to 0, the smoother the contact.
41 of 67
© Boardworks Ltd 2005
Question 5
A children’s slide is inclined at an angle of 25° to the
horizontal. A child of mass 30 kg goes down the slide with a
constant speed.
a) Draw a diagram showing all the forces.
b) Calculate R, the normal contact force.
c) Calculate the coefficient of friction between the child and
the slide.
a)
R
a=0
F
25°
42 of 67
30g
© Boardworks Ltd 2005
Question 5 Solution
b) Resolving perpendicular to the plane,
R = 30g cos25°
R = 266 (to 3 s.f.)
Therefore R is 266 N.
c) Applying Newton’s Second Law down the plane,
30g cos65° – F = 0
F = 124 (to 3 s.f.)
but, F = R
  = 124 ÷ 266 = 0.466 (to 3 s.f.)
43 of 67
© Boardworks Ltd 2005
Question 6
A children’s slide is inclined at an angle  to the horizontal. A
child of mass 25 kg goes down the slide with a constant
speed.
Calculate  given that  = 0.5.
a=0
R
 = 0.5
F
θ
44 of 67
25g
© Boardworks Ltd 2005
Question 6 Solution
Resolving perpendicular to the plane, R = 25g cos
Applying Newton’s Second Law down the slope,
25g cos(90 – )° – F = 0
 F = 25g cos(90 – )°
We know that cos(90 – )° = sin, so F = 25g sin.
=F
R
 0.5= 25g sin
25g cos
We know that sin ÷ cos = tan, so cancelling gives us:
tan = 0.5

45 of 67
 = 26.6° (to 3 s.f.)
© Boardworks Ltd 2005
Question 7
A small wooden block is projected across a horizontal floor.
Initially it has a speed of 3 ms–1, and it comes to rest after
travelling 2 m.
a) Find the acceleration of the block.
b) Find the coefficient of friction between the block and
the floor.
R
m
a
F
mg
46 of 67
© Boardworks Ltd 2005
Question 7 Solution
a) Using v2 = u2 + 2as with s = 2, u = 3 and v = 0:
R
m
a = –2.25
F
0 = 9 + 4a  a = –2.25
The block is therefore
decelerating at 2.25 ms–2.
mg
b) Resolving perpendicularly, R = mg
Applying Newton’s Second Law: 
–F = m × –2.25  F = 2.25m
m = 0.230 (to 3 s.f.)
μ = F = 2.25
mg
R
47 of 67
© Boardworks Ltd 2005
Question 8
A lift is accelerating upwards at 2 ms–2. A woman of mass 60
kg is standing in the lift.
Find the normal contact force between the woman and the
floor of the lift.
Applying Newton’s Second Law: 
R – 60g = 60 × 2
R
60g
48 of 67
a = 2 ms–2
R = 60g + 120
R = 708
Therefore the normal contact force
is 708 N.
© Boardworks Ltd 2005
Question 9
A particle of mass m kg is sliding down a rough plane inclined
at 20° to the horizontal. The coefficient of friction between
the particle and the surface of the plane is 0.2.
Find the acceleration of the particle down the slope.
a=0
μ = 0.2
R
F
20°
49 of 67
mg
© Boardworks Ltd 2005
Question 9 Solution
Resolving perpendicular to the plane, R = mg cos20°
F = R = 0.2mg cos20°
Applying Newton’s Second Law down the plane:
mg cos70° – F = mga

F = mg cos70° – mga = 0.2mg cos20°
mg cos70  0.2mg cos 20
a=
= cos 70° – 0.2 cos 20°
mg
= 0.154 (to 3 s.f.)
 the particle is accelerating at 0.154 ms–2.
50 of 67
© Boardworks Ltd 2005
Contents
Examination-style questions
Pulleys
Internal and external forces
Towing
Friction on a moving particle
Examination-style questions
51
51 of
of 67
67
© Boardworks Ltd 2005
Examination-style question 1
Two particles, A and B, of masses 1 kg and 2 kg respectively,
are connected by a light, inextensible string which passes
over a smooth, fixed pulley.
This pulley is at the top of a rough plane inclined at an angle
of 30° to the horizontal.
A is resting on the plane 2.5 m from the pulley. B is hanging
freely over the pulley 1 m above the ground. The coefficient
of friction between particle A and the slope is 0.25.
a) Find the acceleration of the system when it is released
from rest.
b) Find the time taken for B to reach the ground.
c) Find the distance travelled by A up the slope after B has
reached the ground.
52 of 67
© Boardworks Ltd 2005
Solution 1
a) Resolving perpendicular to the plane, R = gcos30°
Using F = R:
F = ¼gcos30° = 2.12 (to 3 s.f.)
Consider A: T – 2.12 – gcos60° = a
Consider B: 2g – T = 2a
Adding:
2g – 2.12 – gcos60° = 3a
1
a = (2g – 2.12 – gcos60°) = 4.19 (to 3 s.f.)
3
Therefore the acceleration of the system is 4.19 m s–2.
53 of 67
© Boardworks Ltd 2005
Solution 1
For B ,
u=0
a = 4.19
s=1
t=?
Using s = ut + ½at2
1 = 0 + 0.5 × 4.19 × t2
t2 = 0.477…
t = 0.691 (to 3 s.f.)
Therefore B takes 0.691 seconds to reach the ground.
54 of 67
© Boardworks Ltd 2005
Solution 1
55 of 67
© Boardworks Ltd 2005
Solution 1
Consider A until B reaches the ground:
u=0
a = 4.19
v = velocity
t = 0.691
v=?
Using v = u + at:
v = 0 + 4.19 × 0.691
= 2.90 (to 3 s.f.)
So, the velocity of particle A at the moment that B reaches
the ground, is 2.90 m s–1.
56 of 67
© Boardworks Ltd 2005
Solution 1
When B reaches the ground the
string becomes slack and there is no
longer a force pulling A up the slope.
Using F = ma up the slope:
–2.12 – gcos60° = a

a = –7.02 (to 3 s.f.)
For A:
u = 2.90
a = –7.02
v=0
s=?
Using v2 = u2 + 2as:
(v 2  u 2 ) 2.902

s=
2a
14.04
s = 0.599 (to 3 s.f.)
Therefore, A travels a further 0.599 m up the
slope after B stops.
57 of 67
© Boardworks Ltd 2005
Examination-style question 2
Two particles, A and B, have masses 3m kg and km kg
respectively, where k>3. The particles are connected by a
light, inextensible string which passes over a smooth, fixed
pulley.
g
The system has an acceleration of m s–2 when it is
5
released from rest.
a) Find the tension in the string in terms of m and g.
b) Find the value of k.
58 of 67
© Boardworks Ltd 2005
Solution 2
3mg
T – 3mg =
18mg 5
T=
5
b) Consider particle B:
kmg – 18mg  kmg
5
5
4kmg 18mg so, 4kmg = 18mg

5
5
4k = 18
Therefore, k = 4.5
a) Consider particle A:
59 of 67
© Boardworks Ltd 2005
Examination-style question 3
A car of mass 850 kg is being towed by a tow-truck of mass
1500 kg. The car and the tow-truck are joined by a light
towbar, which is at an angle of 20° to the ground.
The car and the tow-truck experience resistances to motion
of 250 N and 600 N respectively.
The driving force exerted by the tow-truck is 3200 N.
a) Find the acceleration of the car and tow-truck.
b) Find the tension in the towbar.
60 of 67
© Boardworks Ltd 2005
Solution 3
Applying Newton’s second law to the whole system:
3200 – 600 – 250 = 2350 × a
2350a = 2350
a=1
Therefore the acceleration of the system is 1 m s–2.
61 of 67
© Boardworks Ltd 2005
Solution 3
Applying Newton’s second law to the car:
Tcos20° – 250 = 850 × 1
850  250
T=
cos20
T = 1170 (to 3 s.f.)
Therefore the tension in the towbar is 1170 N.
62 of 67
© Boardworks Ltd 2005
Examination-style question 4
A particle of mass m kg slides down a rough plane inclined at
25° to the horizontal.
The particle passes through a point A with speed 3 ms–1, and
2 seconds later passes a point B with speed 9 ms–1.
a) Find the acceleration of the particle.
b) Find F in terms of m.
c) Find the coefficient of friction between the particle and the
surface of the slope.
63 of 67
© Boardworks Ltd 2005
Solution 4
93
a) Acceleration =
= 3 ms–2
2
a = 3 ms–2
b)
R
F
25°
mg
Applying Newton’s Second Law down the plane:
mg cos65° – F = m × 3
F = mg cos65° – 3m
c) Resolving perpendicular to the plane:
R = mg cos25°
mg cos65  3m
F
= =
= 0.129 (to 3 s.f.)
R
mg cos25
64 of 67
© Boardworks Ltd 2005
Examination-style Question 5
A sledge of mass 70 kg is pulled up a slope inclined at an
7.
angle  to the horizontal where tan = 40
The slope is modelled as a rough inclined plane and the rope
as a light, inextensible string acting parallel to the line of
greatest slope.
The coefficient of friction between the sledge and the slope is
0.3 and the sledge is accelerating up the slope with an
acceleration of 0.4 ms–2.
Find the tension in the rope.
65 of 67
© Boardworks Ltd 2005
Solution 5
a = 0.4 ms–2
R
T
 = 0.3
F
θ
70g
Before we resolve the forces, look at tan =
7
40 .
From the right-angled triangle with smaller sides of length 7
and 40, which has hypotenuse length 402 + 72 ≈ 41, we can
deduce the values of sin and cos :
sin ≈ 7 ÷ 41
66 of 67
and
cos ≈ 40 ÷ 41
© Boardworks Ltd 2005
Solution 5
Resolving perpendicular to the plane,
R = 70g cos  R = 669.3
F = R = 0.3 × 669.3 = 200.8
Applying Newton’s Second Law up the plane,
T – 200.8 – 70g cos(90 – )° = 70 × 0.4
T – 200.8 – 70g sin = 70 × 0.4
T = 200.8 + 117.1 + 28
 T = 346 (to 3 s.f.)
Therefore the tension in the rope is 346 N.
67 of 67
© Boardworks Ltd 2005