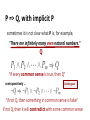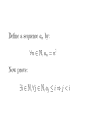Download Lecture slides (full content)

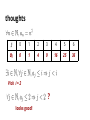
CSC165
Larry Zhang, October 7, 2014
If you did bad,
then it is not bad.
Proof:
assume you left all questions blank
# that’s pretty bad!
then you get 20% # rule on test paper
assume class average is 70% # pretty high!
then you are 50% below average
in this term test # 70% - 20% = 50%
then this term test weighs 6% of final grade
# according course info sheet
then you are 3% below average
in term of final grade # 6%x50%=3%
then it is below are the acceptable
margin of error # 5% in physics
then it is totally acceptable
then it is not bad even if you left everything blank and others did well!
Today’s outline
➔ proof using contrapositive
➔ proof using contradiction
➔ proof for existence
➔ proof about a sequence
Lecture 5.1
contrapositive, contradiction
Course Notes: Chapter 3
Last week
direct proof for universally quantified
implication
as example, we proved
The proof
write comments to
explain each step
# n is a generic natural number
# definition of odd
# square of both sides
# some algebra
# some algebra
# definition of odd
# introduce =>
# introduce ∀
Now, we want to prove...
“not odd”
“not odd”
is the contrapositive of
what we knew
The proof for P => Q also proves ¬Q => ¬P
The proof
# n is a generic natural number
# definition of odd
...
same proof for n odd => n² odd
# definition of odd
# introduce =>
# contrapositive
# introduce ∀
Proof using contrapositive
General idea:
Instead of proving P => Q,
prove ¬Q => ¬P (equivalent to P => Q)
Chain of implication:
When is this useful?
when the reverse direction is easier
to prove than the original.
sometimes the reverse direction is easier to prove
Try the original direction P => Q
# definition of odd
stuck!
?
Try the contrapositive ¬Q => ¬P
# definition of even
# algebra
easy!
# definition of even
takeaway
When it’s not easy to prove P => Q,
try proving ¬Q => ¬P
contradiction
a special case of contrapositive
P => Q, with implicit P
sometimes it is not clear what P is, for example,
“There are infinitely many even natural numbers.”
Q
“If every common sense is true, then Q”
contrapositively ...
De Morgan’s
“if not Q, then something in common sense is false”
if not Q, then it will contradict with some common sense
thoughts
“There are infinitely many even natural numbers.”
Suppose there is a finite number of even numbers…
then there must be a largest one, call it X...
but if I double X…
I get a larger number, a larger even number…
so X is NOT the largest one…
Contradiction!
“There are infinitely many even natural numbers.”
Proof:
assume there are a finite number of even numbers
# assuming ¬Q
then there exists a largest even number, m
then let m’ = 2m
then m’ is an even number, and larger than m
# contradiction, since m is the largest even number
then there are infinitely many even numbers
# assuming ¬Q leads to contradiction, so Q.
There are 5 boxes in which there are in
total 51 balls. Prove that there is a box
with at least 11 balls in it.
Proof:
assume there is not a box with at least 11 balls # not Q
then all boxes have at most 10 balls
# ¬ (∃x, P(x)) ⇔ ∀x, ¬P(x)
then 5 boxes have at most 50 balls
# contradiction with that there are in total 51 balls
then there is a box with at least 11 balls. # Q is true
getting ready for a more challenging one...
Prime number
A prime number is a natural number greater
than 1 that has no positive divisors other
than 1 and itself.
Prime numbers: 2, 3, 5, 7, 11, …, 997, …
Not prime numbers: 0, 1, 4, 6, 8, …, 1000, ...
except 0 and 1, all non-primes ( >2 ) can be divided by a prime.
“There are infinitely many prime numbers.”
thoughts
“There are infinitely many prime numbers.”
Suppose there are finitely many prime numbers…
feels like a prime,
but can’t just say that
Alright, suppose it’s not prime...
then it can be divided by a prime
absurd!
Proof:
# negation of S
# q is the product of all primes
# q is at least 2 x 3 = 6
# every integer > 2
has a prime divisor
# q is the product of all primes
# px divides both q+1 and q
# only 1 divides 1
# contradiction! 1 is not a prime number!
# assume ¬S leads to contradiction
takeaway
When the assumptions are implicit,
try assuming ¬Q, and see whether it leads
somewhere, hunting for a contradiction.
Lecture 5.2 existential, sequence
Course Notes: Chapter 3
direct proof of the existential
How to prove: find a single example.
Prove: There exists a car that is red.
Proof:
pick a car x
then x is red # by human visual checking
then there exists a car that is red # introduce ∃
thoughts
just find a valid x!
Proof:
# choose an example
# well known fact: 2 is real
# plug in x = 2
# example given
prove a claim about a sequence
thoughts
j
0
1
2
3
4
5
6
aj
0
1
4
9
16
25
36
Pick i = 1
?
not good, counter-example: j=1
thoughts
j
0
1
2
3
4
5
6
aj
0
1
4
9
16
25
36
Pick i = 2
?
looks good!
thoughts
j
0
1
2
3
4
5
6
aj
0
1
4
9
16
25
36
Pick i = 4
?
Also good! Ok, let’s use it.
Proof
# a generic element of N
# negate consequent for contrapositive
#i=4
# def of sequence
#i=4
# introduce assumption
# contrapositive, knowing j derive aj
# introduce “for all”
# introduce “exists”
takeaway
➔ one proof may consist of several different
structures
➔ with multiple quantifiers, zoom into
smaller and smaller part of the statement,
layer by layer
next week
➔ more proofs...