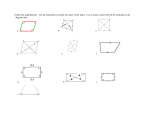
Download Chapter 8: Quadrilaterals

Notes
Quadrilaterals
and Circles
Introduction
In this unit students focus on
quadrilaterals, transformations,
and circles. They learn the properties of the various quadrilaterals
and continue to use coordinate
proofs to prove theorems.
Students explore reflections, translations, rotations, and dilations.
Vectors and transformations with
matrices are introduced.
Students learn the special properties of circles, including the form
of their equations. They also learn
about inscribed and circumscribed
polygons, tangents, and secants.
Two-dimensional
shapes such as
quadrilaterals and
circles can be used to
describe and model
the world around us.
In this unit, you will
learn about the
properties of
quadrilaterals and
circles and how these
two-dimensional
figures can be
transformed.
Assessment Options
Unit 3 Test Pages 609–610
of the Chapter 10 Resource Masters
may be used as a test or review
for Unit 3. This assessment contains both multiple-choice and
short answer items.
ExamView® Pro
Chapter 8
This CD-ROM can be used to
create additional unit tests and
review worksheets.
Quadrilaterals
Chapter 9
Transformations
Chapter 10
Circles
An online, research-based,
instructional, assessment, and
intervention tool that provides
specific feedback on student
mastery of state and national
standards, instant remediation,
and a data management system
to track performance. For more
information, contact
mhdigitallearning.com.
400
Unit 3 Quadrilaterals and Circles
400 Unit 3 Quadrilaterals and Circles
Real-Life Geometry Videos
What’s Math Got to Do With It? Real-Life Geometry
Videos engage students, showing them how math is
used in everyday situations. Use Video 3 with this unit.
Teaching
Suggestions
Have students study the
USA TODAY Snapshot.
• Ask them what the most
popular leisure-time activity
is. reading
• Have volunteers share their
favorite leisure-time activities.
• Tell students that this
WebQuest will send them on
a scavenger hunt of their own.
“Geocaching” Sends Folks
on a Scavenger Hunt
USA TODAY Snapshots®
Source: USA TODAY, July 26, 2001
“N42 DEGREES 02.054 W88 DEGREES 12.329 –
Forget the poison ivy and needle-sharp brambles.
Dave April is a man on a mission. Clutching a
palm-size Global Positioning System (GPS) receiver in
one hand and a computer printout with latitude and
longitude coordinates in the other, the 37-year-old
software developer trudges doggedly through a
suburban Chicago forest preserve, intent on finding
a geek’s version of buried treasure.” Geocaching is
one of the many new ways that people are spending
their leisure time. In this project, you will use
quadrilaterals, circles, and geometric transformations
to give clues for a treasure hunt.
Reading up on leisure activities
What adults say are their top two or
three favorite leisure activities:
31%
Reading
Watching TV
23%
Spending
time with
family/kids
14%
Gardening
Fishing
Walking
Additional USA TODAY
Snapshots appearing in Unit 3:
Chapter 8 Large companies
have increased
using the Internet
to find employees
(p. 411)
Chapter 9 Kids would rather
be smart (p. 474)
Chapter 10 Majority
microwave
leftovers (p. 531)
13%
9%
8%
Source: Harris Interactive
By Cindy Hall and Peter Photikoe, USA TODAY
Log on to www.geometryonline.com/webquest.
Begin your WebQuest by reading the Task.
Then continue working
on your WebQuest as
you study Unit 3.
Lesson
Page
8-6
444
9-1
469
10-1
527
Unit 3 Quadrilaterals and Circles 401
Internet Project
Problem-Based Learning A WebQuest is an online project in which
students do research on the Internet, gather data, and make presentations
using word processing, graphing, page-making, or presentation software. In
each chapter, students advance to the next step in their WebQuest. At the end
of Chapter 10, the project culminates with a presentation of their findings.
Teaching notes and sample answers are available in the WebQuest and
Project Resources.
Unit 3 Quadrilaterals and Circles 401
Quadrilaterals
Chapter Overview and Pacing
Year-long pacing: pages T20–T21.
PACING (days)
Regular
Block
LESSON OBJECTIVES
Basic/
Average
Advanced
Basic/
Average
Advanced
Angles of Polygons (pp. 404–410)
• Find the sum of the measures of the interior angles of a polygon.
• Find the sum of the measures of the exterior angles of a polygon.
Follow-Up: Use a spreadsheet to find interior and exterior angle measurements of a
regular polygon.
1
2 (with 8-1
Follow-Up)
0.5
1 (with 8-1
Follow-Up)
Parallelograms (pp. 411–416)
• Recognize and apply properties of the sides and angles of parallelograms.
• Recognize and apply properties of the diagonals of parallelograms.
2
2
1
1
Tests for Parallelograms (pp. 417–423)
• Recognize the conditions that ensure a quadrilateral is a parallelogram.
• Prove that a set of points forms a parallelogram in the coordinate plane.
2
2
1
1
Rectangles (pp. 424–430)
• Recognize and apply properties of rectangles.
• Determine whether parallelograms are rectangles.
1
1
0.5
0.5
2 (with 8-5 2 (with 8-5 1 (with 8-5 1 (with 8-5
Follow-Up) Follow-Up) Follow-Up) Follow-Up)
Rhombi and Squares (pp. 431–438)
• Recognize and apply the properties of rhombi.
• Recognize and apply the properties of squares.
Follow-Up: Construct a kite.
Trapezoids (pp. 439–445)
• Recognize and apply the properties of trapezoids.
• Solve problems involving the medians of trapezoids.
2
1
1
0.5
Coordinate Proof with Quadrilaterals (pp. 447–451)
• Position and label quadrilaterals for use in coordinate proofs.
• Prove theorems using coordinate proofs.
2
2
1
1
Study Guide and Practice Test (pp. 452–457)
Standardized Test Practice (pp. 458–459)
1
1
0.5
0.5
Chapter Assessment
1
1
0.5
0.5
14
14
7
7
TOTAL
An electronic version of this chapter is available on StudentWorksTM. This backpack solution CD-ROM
allows students instant access to the Student Edition, lesson worksheet pages, and web resources.
402A Chapter 8 Quadrilaterals
Timesaving Tools
™
All-In-One Planner
and Resource Center
Chapter Resource Manager
See pages T5 and T21.
417–418
419–420
421
422
423–424
425–426
427
428
429–430
431–432
433
434
435–436
437–438
439
440
441–442
443–444
445
446
447–448
449–450
451
452
474
453–454
455–456
457
458
474
473
Ap
plic
atio
ns*
5-M
Tra inute
nsp
C
are heck
nci
es
Int
e
Cha racti
lkb ve
oar
Ge
d
om
PA
Plu SS:
s (l
T
ess utori
ons al
)
Ass
ess
me
nt
Pre
req
u
Wo isite
rkb Ski
ook lls
Enr
ich
me
nt
S
and tudy
Int Guid
erv
e
ent
ion
(Sk Pra
c
ills
and tice
Ave
rag
e)
Rea
di
Ma ng to
the
ma Learn
tics
CHAPTER 8 RESOURCE MASTERS
Materials
5–6
8-1
8-1
straightedge, protractor
81–82
8-2
8-2
patty paper, ruler
SC 15
8-3
8-3
straw, scissors, pipe cleaners,
protractors
GCC 31, 32
8-4
8-4
straightedge, compass
8-5
8-5
straightedge, compass, ruler,
protractor
(Follow-Up: compass)
8-6
8-6
8-7
8-7
473, 475
41–42
SC 16
17
ruler, compass
459–472,
476–478
*Key to Abbreviations: GCC Graphing Calculator and Computer Masters
SC School-to-Career Masters
Chapter 8 Quadrilaterals
402B
Mathematical Connections
and Background
Continuity of Instruction
Prior Knowledge
In Chapter 1, students used the Distance
Formula. In Chapter 3, they found the slope
of a line and proved that lines are perpendicular. They also identified the types of
angles formed when a transversal intersects
a pair of parallel lines. Chapter 4 challenged
students to find the measure of a
missing angle.
This Chapter
In this chapter, students explore quadrilaterals.
They begin by investigating the interior and
exterior angles of polygons. Then students
learn to recognize and apply the properties
of parallelograms. Students’ knowledge of
parallelograms is extended as they explore
rectangles, rhombi, and squares and their
special properties. Trapezoids are also
explored. Finally, students position
quadrilaterals on the coordinate plane for
use in coordinate proofs.
Future Connections
In Chapter 11, students find the area of
quadrilaterals. In Chapter 12, they again extend
their knowledge of quadrilaterals by finding
the surface area of prisms. Understanding the
properties of quadrilaterals is essential to
success in engineering, architecture, or design.
402C Chapter 8 Quadrilaterals
Angles of Polygons
The Interior Angle Sum Theorem states that if a
convex polygon has n sides and S is the sum of the
measures of its interior angles, then S 180(n 2). This
equation can also be used to find the measure of each
interior angle in a regular polygon. Moreover, it can be
used to find the number of sides in a polygon if the sum
of the interior angle measures is known.
The sum of the exterior angles of a convex
polygon is always 360, no matter the number of sides.
This is called the Exterior Angle Sum Theorem.
Parallelograms
A parallelogram is a quadrilateral with both
pairs of opposite sides parallel. Parallelograms have
several special properties that help to define them. First,
opposite sides of a parallelogram are congruent, and
opposite angles of a parallelogram are congruent.
Second, consecutive angles in a parallelogram are
supplementary. Third, if a parallelogram has one right
angle, it has four right angles. Finally, the diagonals of
a parallelogram bisect each other, and each diagonal
separates the parallelogram into two congruent
triangles.
Tests for Parallelograms
In addition to the basic definition of a parallelogram as having opposite sides parallel, there are other
tests to determine whether a quadrilateral is a parallelogram. If both pairs of opposite sides of a quadrilateral
are congruent, then the quadrilateral is a parallelogram.
If both pairs of opposite angles of a quadrilateral are
congruent, then it is a parallelogram. If the diagonals of
a quadrilateral bisect each other, the quadrilateral is a
parallelogram. If one pair of opposite sides of a
quadrilateral is both parallel and congruent, then it is a
parallelogram.
A quadrilateral needs to pass only one of these
five tests to be proved a parallelogram. All of the
properties of a parallelogram do not need to be proved.
If a quadrilateral is graphed on the coordinate
plane, you can use the Distance Formula and the Slope
Formula to determine if it is a parallelogram. The Slope
Formula is used to determine whether opposite sides
are parallel. The Distance Formula is used to test
opposite sides for congruence.
Rectangles
A rectangle is a quadrilateral with four right
angles. Since both pairs of opposite sides are congruent,
a rectangle has all the properties of a parallelogram. A
rectangle has special properties of its own as well. For
example, the diagonals of a rectangle are congruent.
Congruent diagonals, in fact, can be used to prove
that a parallelogram is a rectangle.
If a quadrilateral is graphed on a coordinate
plane, the Slope Formula can be used to find out
whether consecutive sides are perpendicular. If they
are, then the quadrilateral is a rectangle. The Distance
Formula can also be used to prove that a quadrilateral
is a rectangle. You can use the Distance Formula to
calculate the measures of the diagonals. If the
diagonals are congruent, then the parallelogram is
a rectangle.
Rhombi and Squares
A rhombus is a quadrilateral with all four
sides congruent. Since opposite sides are congruent,
the rhombus is a parallelogram. Therefore, all the
properties of parallelograms can be applied to rhombi.
Rhombi also have special properties of their own. The
diagonals of a rhombus are perpendicular. The converse
of this theorem also holds true: If the diagonals of a
parallelogram are perpendicular, then the parallelogram
is a rhombus. Each diagonal of a rhombus bisects a
pair of opposite angles.
If a quadrilateral is both a rhombus and a
rectangle, then it is a square. A square is extremely
specialized, having all the properties of a parallelogram, a rectangle, and a rhombus. It is important to
note that while a square is a rhombus, a rhombus is
not necessarily a square.
Coordinate geometry can be used to prove
whether a parallelogram is a rhombus, a rectangle, a
square, or none of those.
Trapezoids
A trapezoid is a quadrilateral with exactly one
pair of parallel sides. The parallel sides are called bases,
and the nonparallel sides are called legs. A base and
a leg form a base angle. If the legs are congruent, then
the trapezoid is an isosceles trapezoid. Both pairs of
base angles of an isosceles trapezoid are congruent.
The diagonals of an isosceles trapezoid are also
congruent.
The segment that joins the midpoints of the
legs of a trapezoid is the median. The median of a
trapezoid is parallel to the bases, and its measure is
one-half the sum of the measures of the bases. This is
true for all trapezoids, not only isosceles trapezoids.
Coordinate Proof with
Quadrilaterals
A coordinate proof is easier to write if the
quadrilateral is correctly placed on the coordinate
plane. Quadrilaterals should be placed so that the
coordinates of the vertices are as simple as possible.
In general, this means placing the quadrilateral in the
first quadrant with one of its vertices at the origin.
The base of the quadrilateral should run along the
x-axis.
Once a figure has been placed on the coordinate plane, theorems can be proved using the Slope,
Midpoint, and Distance Formulas.
Chapter 8 Quadrilaterals
402D
and Assessment
Key to Abbreviations:
TWE = Teacher Wraparound Edition; CRM = Chapter Resource Masters
ASSESSMENT
INTERVENTION
Type
Student Edition
Teacher Resources
Ongoing
Prerequisite Skills, pp. 403, 409,
416, 423, 430, 437, 445
Practice Quiz 1, p. 423
Practice Quiz 2, p. 445
5-Minute Check Transparencies
Prerequisite Skills Workbook, pp. 5–6, 41–42,
81–82
Quizzes, CRM pp. 473–474
Mid-Chapter Test, CRM p. 475
Study Guide and Intervention, CRM pp. 417–418,
423–424, 429–430, 435–436, 441–442,
447–448, 453–454
Mixed
Review
pp. 409, 416, 423, 430, 437,
445, 451
Cumulative Review, CRM p. 476
Error
Analysis
Find the Error, pp. 420, 427
Common Misconceptions, p. 419
Find the Error, TWE pp. 421, 427
Unlocking Misconceptions, TWE p. 434
Tips for New Teachers, TWE p. 406
Standardized
Test Practice
pp. 409, 413, 414, 416, 423,
430, 437, 444, 445, 451, 457,
458, 459
TWE pp. 458–459
Standardized Test Practice, CRM pp. 477–478
Open-Ended
Assessment
Writing in Math, pp. 409, 416,
422, 430, 436, 444, 451
Open Ended, pp. 407, 414, 420,
427, 434, 442, 449
Standardized Test, p. 459
Modeling: TWE pp. 423, 437
Speaking: TWE pp. 409, 445
Writing: TWE pp. 416, 430, 451
Open-Ended Assessment, CRM p. 471
Chapter
Assessment
Study Guide, pp. 452–456
Practice Test, p. 457
Multiple-Choice Tests (Forms 1, 2A, 2B),
CRM pp. 459–464
Free-Response Tests (Forms 2C, 2D, 3),
CRM pp. 465–470
Vocabulary Test/Review, CRM p. 472
For more information on
Yearly ProgressPro, see p. 400.
Geometry Lesson
8-1
8-2
8-3
8-4
8-5
8-6
8-7
Yearly ProgressPro Skill Lesson
Angles of Polygons
Parallelograms
Tests for Parallelograms
Rectangles
Rhombi and Squares
Trapezoids
Coordinate Proof and Quadrilaterals
GeomPASS: Tutorial Plus,
Lesson 17
www.geometryonline.com/
self_check_quiz
www.geometryonline.com/
extra_examples
Standardized Test Practice
CD-ROM
www.geometryonline.com/
standardized_test
ExamView® Pro (see below)
MindJogger Videoquizzes
www.geometryonline.com/
vocabulary_review
www.geometryonline.com/
chapter_test
ExamView® Pro
Use the networkable ExamView® Pro to:
• Create multiple versions of tests.
• Create modified tests for Inclusion students.
• Edit existing questions and add your own questions.
• Use built-in state curriculum correlations to create
tests aligned with state standards.
• Apply art to your test from a program bank of artwork.
For more information on Intervention and Assessment, see pp. T8–T11.
402E Chapter 8 Quadrilaterals
Technology/Internet
Reading and Writing in Mathematics
Glencoe Geometry provides numerous opportunities to incorporate reading and writing
into the mathematics classroom.
Student Edition
Additional Resources
• Foldables Study Organizer, p. 403
• Concept Check questions require students to verbalize
and write about what they have learned in the lesson.
(pp. 407, 414, 420, 427, 434, 442, 449)
• Reading Mathematics, p. 446
• Writing in Math questions in every lesson, pp. 409, 416,
422, 430, 436, 444, 451
• Reading Study Tip, pp. 411, 432
• WebQuest, p. 444
Teacher Wraparound Edition
• Foldables Study Organizer, pp. 403, 452
• Study Notebook suggestions, pp. 404, 414, 421, 427,
434, 438, 442, 446, 449
• Modeling activities, pp. 423, 437
• Speaking activities, pp. 409, 445
• Writing activities, pp. 416, 430, 451
• ELL Resources, pp. 402, 408, 415, 422, 428, 435,
443, 446, 450, 452
• Vocabulary Builder worksheets require students to
define and give examples for key vocabulary terms as
they progress through the chapter. (Chapter 8 Resource
Masters, pp. vii-viii)
• Proof Builder helps students learn and understand
theorems and postulates from the chapter. (Chapter 8
Resource Masters, pp. ix–x)
• Reading to Learn Mathematics master for each lesson
(Chapter 8 Resource Masters, pp. 421, 427, 433, 439,
445, 451, 457)
• Vocabulary PuzzleMaker software creates crossword,
jumble, and word search puzzles using vocabulary lists
that you can customize.
• Teaching Mathematics with Foldables provides
suggestions for promoting cognition and language.
• Reading Strategies for the Mathematics Classroom
• WebQuest and Project Resources
For more information on Reading and Writing in Mathematics, see pp. T6–T7.
Lesson 8-2
Lesson 8-5
Lesson 8-6
Reading and Writing
Reading and Writing
Prior Knowledge
Help students to organize their notes
about quadrilaterals. Students can divide
a piece of notebook paper into three
columns: one with the name of the
quadrilateral, the next with a sketch of the
quadrilateral, and the last with a summary
of the properties of each quadrilateral.
Encourage students to add on to their
charts throughout their study of the
chapter.
Allow the students time to work in pairs
to complete the Writing In Math exercises
as well as the activity and construction.
This enables the English Language
Learners to practice their writing and
speaking skills while fostering a deeper
understanding of the concepts.
Draw a trapezoid on the board.
Demonstrate to students that the legs of
a trapezoid extend to form a triangle. Have
the class list properties of isosceles triangles.
Let the students discover the common
properties between isosceles triangles and
isosceles trapezoids.
Chapter 8 Quadrilaterals
402F
Notes
Have students read over the list
of objectives and make a list of
any words with which they are
not familiar.
Point out to students that this is
only one of many reasons why
each objective is important.
Others are provided in the
introduction to each lesson.
Quadrilaterals
• Lesson 8-1 Investigate interior and exterior
angles of polygons.
• Lessons 8-2 and 8-3 Recognize and apply the
properties of parallelograms.
• Lessons 8-4 through 8-6 Recognize and apply
the properties of rectangles, rhombi, squares,
and trapezoids.
• Lesson 8-7 Position quadrilaterals for use in
coordinate proof.
Key Vocabulary
•
•
•
•
•
parallelogram (p. 411)
rectangle (p. 424)
rhombus (p. 431)
square (p. 432)
trapezoid (p. 439)
Several different geometric shapes are
examples of quadrilaterals. These shapes each
have individual characteristics. A rectangle is a type
of quadrilateral. Tennis courts are rectangles, and the
properties of the rectangular court are used in the
game. You will learn more about tennis courts in Lesson 8-4.
Lesson
8-1
8-1
Follow-Up
8-2
8-3
8-4
8-5
8-5
Follow-Up
8-6
8-7
NCTM
Standards
Local
Objectives
2, 3, 6, 8, 9, 10
2, 3, 6
2, 3, 6, 8, 9, 10
2, 3, 6, 7, 8, 9,
10
2, 3, 6, 8, 9, 10
2, 3, 6, 7, 8, 9,
10
3, 6
402 Chapter 8
2, 3, 6, 7, 8, 9,
10
2, 3, 6, 7, 8, 9,
10
Key to NCTM Standards:
1=Number & Operations, 2=Algebra,
3=Geometry, 4=Measurement,
5=Data Analysis & Probability, 6=Problem
Solving, 7=Reasoning & Proof,
8=Communication, 9=Connections,
10=Representation
402
Chapter 8 Quadrilaterals
Quadrilaterals
Michael Newman/PhotoEdit
Vocabulary Builder
ELL
The Key Vocabulary list introduces students to some of the main vocabulary terms
included in this chapter. For a more thorough vocabulary list with pronunciations of
new words, give students the Vocabulary Builder worksheets found on pages vii and
viii of the Chapter 8 Resource Masters. Encourage them to complete the definition
of each term as they progress through the chapter. You may suggest that they add
these sheets to their study notebooks for future reference when studying for the
Chapter 8 test.
Prerequisite Skills To be successful in this chapter, you’ll need to master
these skills and be able to apply them in problem-solving situations. Review
these skills before beginning Chapter 8.
For Lesson 8-1
Exterior Angles of Triangles
Find x for each figure. (For review, see Lesson 4-2.)
130 2.
1.
x˚
45 3.
25˚
x˚
50˚
120
20˚
This section provides a review of
the basic concepts needed before
beginning Chapter 8. Page
references are included for
additional student help.
Additional review is provided in
the Prerequisite Skills Workbook,
pages 5–6, 41–42, 81–82.
x˚
7 5
1
4.⫺ ᎏᎏ, ᎏᎏ; perpendicular 5. ᎏᎏ,⫺6; perpendicular
5 7
6
For Lessons 8-4 and 8-5
Perpendicular Lines
S and T
RS
Find the slopes of 苶
R苶
苶S
苶 for the given points, R, T, and S. Determine whether 苶
苶
and T
苶S
苶 are perpendicular or not perpendicular. (For review, see Lesson 3-6.)
4. R(4, 3), S(1, 10), T(13, 20)
5. R(9, 6), S(3, 8), T(1, 20)
6. R(6, 1), S(5, 3), T(2, 5)
4
2
ᎏᎏ, ⫺ ᎏᎏ; not perpendicular
11
3
For Lesson 8-7
7. R(6, 4), S(3, 8), T(5, 2)
4
3
ᎏᎏ, ⫺ ᎏᎏ; perpendicular
3
4
Slope
Prerequisite Skills in the Getting
Ready for the Next Lesson section
at the end of each exercise set
review a skill needed in the next
lesson.
For
Lesson
Prerequisite
Skill
8-2
Angles formed by parallel lines
and a transversal, p. 409
Slope, p. 416
Using slope to determine
perpendicularity, p. 423
Distance Formula, p. 430
Solving equations, p. 437
Slope, p. 445
Write an expression for the slope of a segment given the coordinates of the endpoints.
(For review, see Lesson 3-3.)
d
c d
8. 冢, 冣, (c, d) ⫺ ᎏᎏ
2 2
3c
a
9. (0, a), (b, 0) ⫺ ᎏᎏ
b
10. (a, c), (c, a) 1
Quadrilaterals Make this Foldable to help you organize your notes. Begin with a
sheet of notebook paper.
Fold
8-3
8-4
8-5
8-6
8-7
Cut
Fold lengthwise to the left
margin.
Cut 4 tabs.
Label
Label the tabs using the
lesson concepts.
s
logram
paralle
gles
rectan
and
squares bi
rhom
ds
trapezoi
Reading and Writing As you read and study the chapter, use your Foldable to take notes, define terms,
and record concepts about quadrilaterals.
Chapter 8 Quadrilaterals 403
TM
For more information
about Foldables, see
Teaching Mathematics
with Foldables.
Organization of Data for Comparing and Contrasting Use this
Foldable to organize data about quadrilaterals. After students make
their Foldable, have them label the tabs as illustrated. Students can
use their Foldable to take notes, define terms, record concepts, and
apply properties of quadrilaterals. Use the data recorded to compare
and contrast the four quadrilaterals studied. For example, how are
parallelograms and rectangles similar? different?
Chapter 8 Quadrilaterals 403
Lesson
Notes
Angles of Polygons
B
• Find the sum of the measures of the interior angles of a polygon.
1 Focus
5-Minute Check
Transparency 8-1 Use as a
quiz or review of Chapter 7.
• Find the sum of the measures of the exterior angles of a polygon.
Vocabulary
• diagonal
Mathematical Background notes
are available for this lesson on
p. 402C.
does a scallop shell
illustrate the angles of
polygons?
Ask students:
• How many diagonals can be
drawn from one vertex of a
12-sided polygon? 9
• What other polygons are
represented in nature? Sample
answer: Honeycombs resemble
hexagons.
does a scallop shell illustrate
the angles of polygons?
This scallop shell resembles a 12-sided polygon with
diagonals drawn from one of the vertices. A diagonal
of a polygon is a segment that connects any two
nonconsecutive vertices. For example, A
B
is one of
the diagonals of this polygon.
A
SUM OF MEASURES OF INTERIOR ANGLES
Polygons with more than
three sides have diagonals. The polygons below show all of the possible diagonals
drawn from one vertex.
quadrilateral
Study Tip
Look Back
To review the sum of
the measures of the
angles of a triangle,
see Lesson 4-2.
pentagon
hexagon
heptagon
octagon
In each case, the polygon is separated into triangles. Each angle of the polygon is
made up of one or more angles of triangles. The sum of the measures of the angles of
each polygon can be found by adding the measures of the angles of the triangles. Since
the sum of the measures of the angles in a triangle is 180, we can easily find this sum.
Make a table to find the sum of the angle measures for several convex polygons.
Convex
Polygon
Number of
Sides
Number of
Triangle
Sum of Angle
Measures
triangle
3
1
quadrilateral
4
2
(2 180) or 360
pentagon
5
3
(3 180) or 540
hexagon
6
4
(4 180) or 720
heptagon
7
5
(5 180) or 900
octagon
8
6
(6 180) or 1080
(1 180) or 180
Look for a pattern in the sum of the angle measures. In each case, the sum of the
angle measures is 2 less than the number of sides in the polygon times 180. So in an
n-gon, the sum of the angle measures will be (n 2)180 or 180(n 2).
Theorem 8.1
Interior Angle Sum Theorem If a convex
polygon has n sides and S is the sum of
the measures of its interior angles, then
S 180(n 2).
404
Example:
n 5
S 180(n 2)
180(5 2) or 540
Chapter 8 Quadrilaterals
Glencoe photo
Resource Manager
Workbook and Reproducible Masters
Chapter 8 Resource Masters
• Study Guide and Intervention, pp. 417–418
• Skills Practice, p. 419
• Practice, p. 420
• Reading to Learn Mathematics, p. 421
• Enrichment, p. 422
Prerequisite Skills Workbook, pp. 5–6
Teaching Geometry With Manipulatives
Masters, pp. 16, 127, 128
Transparencies
5-Minute Check Transparency 8-1
Answer Key Transparencies
Technology
Interactive Chalkboard
Example 1 Interior Angles of Regular Polygons
CHEMISTRY The benzene molecule, C6H6, consists of six carbon atoms in a
regular hexagonal pattern with a hydrogen atom attached to each carbon atom.
Find the sum of the measures of the interior angles of the hexagon.
Since the molecule is a convex polygon, we can use
H
H
the Interior Angle Sum Theorem.
S 180(n 2)
Interior Angle Sum Theorem
180(6 2)
n6
180(4) or 720
Simplify.
H
C
C
C
C
C
C
H
2 Teach
SUM OF MEASURES OF
INTERIOR ANGLES
Teaching Tip
The proof of the
Interior Angle Sum Theorem uses
induction, which is not covered in
this book.
H
H
The sum of the measures of the interior angles is 720.
The Interior Angle Sum Theorem can also be used to find the number of sides in a
regular polygon if you are given the measure of one interior angle.
In-Class Examples
Power
Point®
Teaching Tip
Example 2 Sides of a Polygon
The measure of an interior angle of a regular polygon is 108. Find the number of
sides in the polygon.
Use the Interior Angle Sum Theorem to write an equation to solve for n, the
number of sides.
S 180(n 2)
(108)n 180(n 2)
108n 180n 360
0 72n 360
Interior Angle Sum Theorem
S108n
Distributive Property
Subtract 108n from each side.
360 72n
Add 360 to each side.
5n
Divide each side by 72.
Point out that
while a polygon can be made
up of any number of sides, the
Interior Angle Sum Theorem
applies to convex polygons. That
means that a segment connecting
two points in the interior of the
polygon is entirely contained
within the polygon. Their
diagonals separate the polygon
into countable triangles.
1 ARCHITECTURE A mall is
designed so that five
walkways meet at a food court
that is in the shape of a regular
pentagon. Find the sum of the
measures of the interior angles
of the pentagon. 540
The polygon has 5 sides.
In Example 2, the Interior Angle Sum Theorem was applied to a regular
polygon. In Example 3, we will apply this theorem to a quadrilateral that is
not a regular polygon.
Example 3 Interior Angles
ALGEBRA Find the measure of each interior angle.
Since n 4, the sum of the measures of the interior
angles is 180(4 2) or 360. Write an equation to
express the sum of the measures of the interior angles
of the polygon.
B
2x˚
x˚
A
Food
Court
C
2x˚
x˚
D
Teaching Tip
360 m⬔A m⬔B m⬔C m⬔D Sum of measures of angles
360 x 2x 2x x
Substitution
360 6x
Combine like terms.
60 x
In Example 2,
point out that you could not use
this method to find the number
of sides if the polygon was not
regular.
Divide each side by 6.
Use the value of x to find the measure of each angle.
2 The measure of an interior
m⬔A 60, m⬔B 2 60 or 120, m⬔C 2 60 or 120, and m⬔D 60.
www.geometryonline.com/extra_examples
Lesson 8-1 Angles of Polygons
405
angle of a regular polygon is
135. Find the number of sides
in the polygon. 8
3 Find the measure of each
Teacher to Teacher
Monique Siedschlag, Thoreau High School
interior angle.
S
Thoreau, NM
I ask students "If the sum of the measures of the angles in a triangle is 180, what
would a quadrilateral angle measure sum be? pentagon angle measure sum?" Then I
pass out pre-cut polygons (4 to 9 sides) and have students measure the angles. The
students soon discover that the sum is not 180, as many thought it would be. We list
the results and students start to see a pattern. I then have them create a workable
formula. Many do come up with the Interior Angle Sum Theorem.
R
5x 5x (11x 4)
T
(11x 4)
U
mR mT 55;
mS mU 125
Lesson 8-1 Angles of Polygons 405
SUM OF MEASURES OF EXTERIOR ANGLES The Interior Angle Sum
Theorem relates the interior angles of a convex polygon to the number of sides. Is
there a relationship among the exterior angles of a convex polygon?
SUM OF MEASURES OF
EXTERIOR ANGLES
Study Tip
Intervention
The Geometry
New
Activity gives
students
experience
with discovering patterns by
collecting and analyzing data.
Students should recognize
that in a polygon, the number
of sides equals the number of
exterior angles.
In-Class Example
Look Back
Sum of the Exterior Angles of a Polygon
To review exterior angles,
see Lesson 4-2.
Collect Data
• Draw a triangle, a convex quadrilateral, a convex
pentagon, a convex hexagon, and a convex heptagon.
• Extend the sides of each polygon to form exactly
one exterior angle at each vertex.
• Use a protractor to measure each exterior angle
of each polygon and record it on your drawing.
Analyze the Data
1. Copy and complete the table.
Polygon
number of
exterior angles
Power
Point®
sum of measure
of exterior angles
4 Find the measures of an
quadrilateral
pentagon
hexagon
heptagon
3
4
5
6
7
360
360
360
360
360
is 360.
The Geometry Activity suggests Theorem 8.2.
D
B
Theorem 8.2
E
A
Exterior Angle Sum Theorem If a
polygon is convex, then the sum of the
measures of the exterior angles, one at
each vertex, is 360.
F
J
H
triangle
2. What conjecture can you make? The sum of the measures of exterior angles
exterior angle and an interior
angle of convex regular
nonagon ABCDEFGHJ.
C
72°
G
Example:
2
1
3
5
4
40; 140
m⬔1m⬔2 m⬔3 m⬔4 m⬔5 360
You will prove Theorem 8.2 in Exercise 42.
Example 4 Exterior Angles
Find the measures of an exterior angle and an interior
angle of convex regular octagon ABCDEFGH.
At each vertex, extend a side to form one exterior angle.
The sum of the measures of the exterior angles is 360.
A convex regular octagon has 8 congruent exterior angles.
8n 360
n45
Interactive
n = measure of each exterior angle
B
D
H
E
G
PowerPoint®
Presentations
Divide each side by 8.
406 Chapter 8 Quadrilaterals
406
Chapter 8 Quadrilaterals
F
The measure of each exterior angle is 45. Since each exterior angle and its
corresponding interior angle form a linear pair, the measure of the interior
angle is 180 45 or 135.
Chalkboard
This CD-ROM is a customizable
Microsoft® PowerPoint®
presentation that includes:
• Step-by-step, dynamic solutions of
each In-Class Example from the
Teacher Wraparound Edition
• Additional, Try These exercises for
each example
• The 5-Minute Check Transparencies
• Hot links to Glencoe Online
Study Tools
C
A
Geometry Activity
Materials: straightedge, protractor
It may help students see the relationship between the interior angles and the
exterior angles if you have them add a row to the bottom of the table in the
activity. Have it include the measures of the exterior angles of the polygon if
the polygon is regular.
Concept Check
Guided Practice
GUIDED PRACTICE KEY
Exercises
Examples
4–5, 12
6–7
8–9
10–11
1
2
3
4
8. mT mV 46,
mU mW 134
9. mJ mM 30, mK mL mP mN 165
1. Explain why the Interior Angle Sum Theorem and the Exterior Angle Sum
Theorem only apply to convex polygons. 1–2. See margin.
2. Determine whether the Interior Angle Sum Theorem and the Exterior Angle
Sum Theorem apply to polygons that are not regular. Explain.
3. OPEN ENDED Draw a regular convex polygon and a convex polygon that is not
regular with the same number of sides. Find the sum of the interior angles for each.
See p. 459A.
Find the sum of the measures of the interior angles of each convex polygon.
5. dodecagon 1800
4. pentagon 540
The measure of an interior angle of a regular polygon is given. Find the number
of sides in each polygon.
7. 90 4
6. 60 3
ALGEBRA Find the measure of each interior angle.
U
V
8.
9.
(3x 4)˚
x˚
J
K
2x˚
x˚
T
(3x 4)˚
L
(9x 30)˚ (9x 30)˚
(9x 30)˚ (9x 30)˚
P
2x˚
M
N
W
Find the measures of an exterior angle and an interior angle given the number of
sides of each regular polygon.
11. 18 20, 160
10. 6 60, 120
Application
12. AQUARIUMS The regular polygon at the right is the
base of a fish tank. Find the sum of the measures of the
interior angles of the pentagon. 540
13–20
21–26
27–34
35–44
1
2
3
4
Odd/Even Assignments
Exercises 13–44 are structured
so that students practice the
same concepts whether they
are assigned odd or even
problems.
Find the sum of the measures of the interior angles of each convex polygon.
14. 18-gon 2880
15. 19-gon 3060
13. 32-gon 5400
16. 27-gon 4500
★ 17. 4y-gon 360(2y 1) ★ 18. 2x-gon 360(x 1)
19. GARDENING Carlotta is designing a garden for her backyard. She wants a
flower bed shaped like a regular octagon. Find the sum of the measures of the
interior angles of the octagon. 1080
Extra Practice
See page 769.
Have students—
• add the definitions/examples of
the vocabulary terms to their
Vocabulary Builder worksheets for
Chapter 8.
• include a table that shows the sum
of the measures of the interior
angles for polygons with 3, 4, 5, 6, 7,
and 8 sides as shown on p. 404.
• include any other item(s) that they
find helpful in mastering the skills
in this lesson.
Organization by Objective
• Sum of Measures of
Interior Angles: 13–34
• Sum of Measures of
Exterior Angles: 35–44
Practice and Apply
See
Examples
Study Notebook
About the Exercises…
★ indicates increased difficulty
For
Exercises
3 Practice/Apply
20. GAZEBOS A company is building regular hexagonal gazebos. Find the sum of
the measures of the interior angles of the hexagon. 720
The measure of an interior angle of a regular polygon is given. Find the number
of sides in each polygon.
22. 170 36
23. 160 18
21. 140 9
1
2
24. 165 24
25. 157 16
26. 176 100
2
Assignment Guide
Basic: 13–15 odd, 19–31 odd,
35–45 odd, 46–65
Average: 13–45 odd, 46–65
Advanced: 14–44 even, 45–61
(optional: 62–65)
5
Lesson 8-1 Angles of Polygons
407
Differentiated Instruction
Logical Students should reason that as the number of sides in a regular
convex polygon increases, the measure of each interior angle increases and
the measure of each exterior angle decreases. For example, a regular
polygon with 360 sides will have an interior angle of 179 and an exterior
angle of 1. Make the connection that as the number sides increases
without bound, there is a limit to the measure that each interior angle can
reach, which happens when the length of the side becomes infinitely small
so that the polygon looks like a circle and the exterior angles disappear.
Answers
1. A concave polygon has at least one
obtuse angle, which means the sum
will be different from the formula.
2. Yes; an irregular polygon can be
separated by the diagonals into
triangles so the theorems apply.
Lesson 8-1 Angles of Polygons 407
NAME ______________________________________________ DATE
p. 417
Angles(shown)
of Polygons and p. 418
Sum of Measures of Interior Angles
The segments that connect the
nonconsecutive sides of a polygon are called diagonals. Drawing all of the diagonals from
one vertex of an n-gon separates the polygon into n 2 triangles. The sum of the measures
of the interior angles of the polygon can be found by adding the measures of the interior
angles of those n 2 triangles.
If a convex polygon has n sides, and S is the sum of the measures of its interior angles,
then S 180(n 2).
Example 1 A convex polygon has
13 sides. Find the sum of the measures
of the interior angles.
S 180(n 2)
180(13 2)
180(11)
1980
Example 2 The measure of an
interior angle of a regular polygon is
120. Find the number of sides.
The number of sides is n, so the sum of the
measures of the interior angles is 120n.
S 180(n 2)
120n 180(n 2)
120n 180n 360
60n 360
n6
Exercises
Find the sum of the measures of the interior angles of each convex polygon.
1. 10-gon
2. 16-gon
1440
3. 30-gon
2520
4. 8-gon
5040
5. 12-gon
1080
6. 3x-gon
The measure of an interior angle of a regular polygon is given. Find the number
of sides in each polygon.
8. 160
12
9. 175
18
10. 165
72
11. 168.75
24
12. 135
32
13. Find x.
8
D
(4x 5)
20
E 7x (5x 5) C
(6x 10)
(4x 10)
A
Gl
27. mM 30, mP
120, mQ 60,
mR 150
28. mE 102,
mF 122, mG 107, mH 97,
mJ 112
29. mM 60, mN
120, mP 60,
mQ 120
30. mT 72, mW
72, mY 108,
mZ 108
J
29. parallelogram MNPQ with
mM 10x and mN 20x
M
180(3x 2)
1800
7. 150
Lesson 8-1
Interior Angle
Sum Theorem
ALGEBRA Find the measure of each interior angle using the given information.
27. M
28.
P
F
G
(x 20)˚ (x 5)˚
x˚
4x˚
E x˚
(x 5)˚
5x˚
2x˚
H
(
x
10)˚
R
Q
____________ PERIOD _____
Study
Guide
andIntervention
Intervention,
8-1
Study
Guide and
B
NAME
______________________________________________
DATE
/M
G
Hill
417
____________
Gl PERIOD
G _____
Skills
Practice,
8-1
Practice
(Average)
p. 419 and
Practice,
p. 420 (shown)
Angles of Polygons
2. 14-gon
1620
2700
The measure of an interior angle of a regular polygon is given. Find the number
of sides in each polygon.
4. 144
5. 156
10
J
(2x 15)
(3x 20)
8. quadrilateral RSTU with
mR 6x 4, mS 2x 8
K
(x 15)
x
U
★ 42.
T
mR 128, mS 52,
mT 128, mU 52
10. 24-gon
11. 30-gon
165, 15
PROOF
Use algebra to prove the Exterior Angle Sum Theorem. See margin.
43. ARCHITECTURE The Pentagon building
in Washington, D.C., was designed to
resemble a regular pentagon. Find the
measure of an interior angle and an
exterior angle of the courtyard. 108, 72
Find the measures of an interior angle and an exterior angle for each regular
polygon. Round to the nearest tenth if necessary.
157.5, 22.5
Sample answer: 36, 72, 108, 144
quadrilateral in which the measure of each consecutive angle increases by 10
S
R
M
mJ 115, mK 130,
mM 50, mN 65
9. 16-gon
decagon in which the measures of the interior angles are x 5, x 10, x 20,
x 30, x 35, x 40, x 60, x 70, x 80, and x 90
polygon ABCDE with mA6x, mB4x13, mC x9, mD2x 8, and
mE4x 1
quadrilateral in which the measures of the angles are consecutive multiples of x
Find the measures of an interior angle and an exterior angle given the number of
sides of each regular polygon. Round to the nearest tenth if necessary.
40. 7 128.6, 51.4
41. 12 150, 30
39. 11 147.3, 32.7
18
Find the measure of each interior angle using the given information.
N
Y
6. 160
15
7.
Z
75, 85, 95, 105
3. 17-gon
2160
P
W
Find the measures of each exterior angle and each interior angle for each
regular polygon.
36. hexagon 60, 120
35. decagon 36, 144
37. nonagon 40, 140
38. octagon 45, 135
Find the sum of the measures of the interior angles of each convex polygon.
1. 11-gon
T
N
Q
31. 105, 110, 120, 130, 31.
135, 140, 160, 170,
180, 190
32.
32. mA186,
mB137, mC ★ 33.
40, mD54,
mE 123
★ 34.
30. isosceles trapezoid TWYZ
with Z Y, mZ 30x,
T W, and mT 20x
168, 12
Find the measures of an interior angle and an exterior angle given the number of
sides of each regular polygon. Round to the nearest tenth if necessary.
12. 14
13. 22
154.3, 25.7
14. 40
163.6, 16.4
171, 9
15. CRYSTALLOGRAPHY Crystals are classified according to seven crystal systems. The
basis of the classification is the shapes of the faces of the crystal. Turquoise belongs to
the triclinic system. Each of the six faces of turquoise is in the shape of a parallelogram.
Find the sum of the measures of the interior angles of one such face.
360
NAME
______________________________________________
DATE
/M
G
Hill
420
Gl
____________
Gl PERIOD
G _____
Reading
8-1
Readingto
to Learn
Learn Mathematics
Mathematics,
p. 421
Angles of Polygons
Pre-Activity
ELL
How does a scallop shell illustrate the angles of polygons?
Read the introduction to Lesson 8-1 at the top of page 404 in your textbook.
• How many diagonals of the scallop shell shown in your textbook can be
drawn from vertex A? 9
Architecture
Thomas Jefferson’s home,
Monticello, features a
dome on an octagonal
base. The architectural
elements on either side
of the dome were based
on a regular octagon.
Source: www.monticello.org
• How many diagonals can be drawn from one vertex of an n-gon? Explain
your reasoning. n 3; Sample answer: An n-gon has n vertices,
45. CRITICAL THINKING Two formulas can be used to find the measure of an
360
180(n 2)
interior angle of a regular polygon: s and s180 . Show that
n
n
these are equivalent. See margin.
but diagonals cannot be drawn from a vertex to itself or to
either of the two adjacent vertices. Therefore, the number of
diagonals from one vertex is 3 less than the number of
vertices.
Reading the Lesson
1. Write an expression that describes each of the following quantities for a regular n-gon. If
the expression applies to regular polygons only, write regular. If it applies to all convex
polygons, write all.
a. the sum of the measures of the interior angles 180(n 2); all
180(n 2)
n
b. the measure of each interior angle ; regular
44. ARCHITECTURE Compare the dome to the architectural elements on each side
of the dome. Are the interior and exterior angles the same? Find the measures of
the interior and exterior angles. yes; 135, 45
408
Chapter 8 Quadrilaterals
(l)Monticello/Thomas Jefferson Foundation, Inc., (r)SpaceImaging.com/Getty Images
c. the sum of the measures of the exterior angles (one at each vertex) 360; all
360
n
d. the measure of each exterior angle ; regular
2. Give the measure of an interior angle and the measure of an exterior angle of each polygon.
a. equilateral triangle 60; 120
c. square 90; 90
b. regular hexagon 120; 60
d. regular octagon 135; 45
3. Underline the correct word or phrase to form a true statement about regular polygons.
a. As the number of sides increases, the sum of the measures of the interior angles
(increases/decreases/stays the same).
b. As the number of sides increases, the measure of each interior angle
(increases/decreases/stays the same).
c. As the number of sides increases, the sum of the measures of the exterior angles
(increases/decreases/stays the same).
d. As the number of sides increases, the measure of each exterior angle
(increases/decreases/stays the same).
e. If a regular polygon has more than four sides, each interior angle will be a(n)
(acute/right/obtuse) angle, and each exterior angle will be a(n) (acute/right/obtuse) angle.
Helping You Remember
4. A good way to remember a new mathematical idea or formula is to relate it to something
you already know. How can you use your knowledge of the Angle Sum Theorem (for a
triangle) to help you remember the Interior Angle Sum Theorem? Sample answer:
The sum of the measures of the (interior) angles of a triangle is 180.
Each time another side is added, the polygon can be subdivided into one
more triangle, so 180 is added to the interior angle sum.
408
Chapter 8 Quadrilaterals
NAME ______________________________________________ DATE
8-1
Enrichment
Enrichment,
p. 422
Tangrams
The tangram puzzle is composed of seven
pieces that form a square, as shown at the
right. This puzzle has been a popular
amusement for Chinese students for
hundreds and perhaps thousands of years.
____________ PERIOD _____
Answer the question that was posed at the beginning of
the lesson. See margin.
How does a scallop shell illustrate the angles of polygons?
46. WRITING IN MATH
4 Assess
Include the following in your answer:
• explain how triangles are related to the Interior Angle Sum Theorem, and
• describe how to find the measure of an exterior angle of a polygon.
Standardized
Test Practice
47. A regular pentagon and a square share a mutual vertex X.
The sides XY
and X
Z
are sides of a third regular polygon with
a vertex at X. How many sides does this polygon have? B
A 19
B 20
C
28
D
Open-Ended Assessment
Speaking Have students describe
how to find the sum of the
measures of the interior angles of
a polygon.
Y
X
Getting Ready for
Lesson 8-2
Z
32
9y
2x
48. GRID IN If 6x 3y 48 and 9, then x ? 4
Maintain Your Skills
Mixed Review
53. mG ⬇ 66,
mH ⬇ 60, h ⬇ 16.1
54. mG 55,
f ⬇ 27.7, h ⬇ 37.0
55. mF 57, f ⬇
63.7, h ⬇ 70.0
56. mH ⬇ 73,
mF ⬇ 42, f ⬇ 22.7
In ABC, given the lengths of the sides, find the measure of the given angle to
the nearest tenth. (Lesson 7-7)
49. a 6, b 9, c 11; mC 92.1
50. a 15.5, b 23.6, c 25.1; mB 66.3
51. a 47, b 53, c 56; mA 51.0
52. a 12, b 14, c 16; mC 75.5
Solve each FGH described below. Round angle measures to the nearest degree
and side measures to the nearest tenth. (Lesson 7-6)
53. f 15, g 17, mF 54
54. mF 47, mH 78, g 31
55. mG56, mH 67, g 63
56. g 30.7, h 32.4, mG 65
57. PROOF Write a two-column proof. (Lesson 4-5) See p. 459A.
KM
Given: JL
㛳
J
K
K㛳 LM
J
Prove: JKL MLK
L
State the transversal that forms each pair of angles.
Then identify the special name for the angle pair.
(Lesson 3-1)
58.
59.
60.
61.
Getting Ready for
the Next Lesson
62. 1 and 4, 1
and 2, 2 and 3,
3 and 4
3 and 11 b; corr.
6 and 7 m; cons. int.
8 and 10 c; alt. int.
12 and 16 n; alt. ext.
M
4 5
3 6
12 13
11 14
10 15
9 16
2 7
1 8
m
b
c
n
PREREQUISITE SKILL In the figure, A
AD
DC
BC
苶B
苶㛳苶
苶 and 苶
苶㛳苶
苶. Name all pairs of
angles for each type indicated. (To review angles formed by parallel lines and a
transversal, see Lesson 3-1.)
62.
63.
64.
65.
consecutive interior angles
alternate interior angles 3 and 5, 2 and 6
corresponding angles 1 and 5, 4 and 6
alternate exterior angles none
www.geometryonline.com/self_check_quiz
A
B
1
D 4
5
2
3 6
C
Lesson 8-1 Angles of Polygons
409
Prerequisite Skill Students will
learn about parallelograms in
Lesson 8-2. They will use the
angles formed by parallel lines
and a transversal to find the
angles in a quadrilateral with
parallel sides. Use Exercises 62–65
to determine your students’
familiarity with the angles formed
by parallel lines and a transversal.
Answer
46. Sample answer: The outline of a
scallop shell is a convex polygon
that is not regular. The lines in the
shell resemble diagonals drawn
from one vertex of a polygon.
These diagonals separate the
polygon into triangles. Answers
should include the following.
• The Interior Angle Sum Theorem
is derived from the pattern
between the number of sides in
a polygon and the number of
triangles. The formula is the
product of the sum of the
measures of the angles in a
triangle, 180, and the number of
triangles the polygon contains.
• The exterior angle and the
interior angle of a polygon are a
linear pair. So, the measure of
an exterior angle is the
difference between 180 and the
measure of the interior angle.
Answers (p. 408)
42. Consider the sum of the measures of the exterior angles, N, for an n-gon.
N sum of measures of linear pairs sum of measures of interior angles
180n 180(n 2)
180n 180n 360
360
So, the sum of the exterior angle measures is 360 for any convex polygon.
180(n 2)
n
180n 360
n
180n
360
n
n
360
180 n
45. Lesson 8-1 Angles of Polygons 409
Spreadsheet
Investigation
A Follow-Up of Lesson 8-1
Getting Started
Students may use the “Fill-down”
feature of a spreadsheet to enter
the data in columns one and two.
For example, if the cell reference
for 3 sides is A2, then enter
“A2 1” in cell A3. Then
highlight cell A3 and drag to
“fill down” the column with the
same pattern. Students should
notice that they can find the sum
of the interior angles for a
many-sided polygon this way,
including a polygon with 110
sides (Exercise 7).
A Follow-Up of Lesson 8-1
Angles of Polygons
It is possible to find the interior and exterior measurements along with the sum of
the interior angles of any regular polygon with n number of sides using a spreadsheet.
Example
Design a spreadsheet using the following steps.
• Label the columns as shown in the spreadsheet below.
• Enter the digits 3–10 in the first column.
• The number of triangles formed by diagonals from the same vertex in a polygon is
2 less than the number of sides. Write a formula for Cell B2 to subtract 2 from each
number in Cell A2.
• Enter a formula for Cell C2 so the spreadsheet will find the sum of the measures of
the interior angles. Remember that the formula is S (n 2)180.
• Continue to enter formulas so that the indicated computation is performed. Then,
copy each formula through Row 9. The final spreadsheet will appear as below.
Teach
• You may want students to do
this activity in pairs, especially
if there is limited availability of
computers. Ask one student to
enter the data into the computer
while another student reads
the information to be entered.
Ask the pairs of students to
discuss which formulas should
be used for Exercises 1–2.
Assess
The answers for Exercises 5–7
will be correct only if students
entered their formulas correctly
into the spreadsheet.
Exercises
1.
2.
3.
4.
Write the formula to find the measure of each interior angle in the polygon. C2/A2
Write the formula to find the sum of the measures of the exterior angles. A2*E2
What is the measure of each interior angle if the number of sides is 1? 2? 180, 0
Is it possible to have values of 1 and 2 for the number of sides? Explain. No, a
polygon is a closed figure formed by coplanar segments.
For Exercises 5 – 8, use the spreadsheet.
5. How many triangles are in a polygon with 15 sides? 13
6. Find the measure of the exterior angle of a polygon with 15 sides. 24
7. Find the measure of the interior angle of a polygon with 110 sides. 176.7
8. If the measure of the exterior angles is 0, find the measure of the interior angles.
Is this possible? Explain. Each interior angle measures 180. This is not possible
410 Chapter 8 Quadrilaterals
410 Chapter 8 Quadrilaterals
for a polygon.
Lesson
Notes
Parallelograms
• Recognize and apply properties
USA TODAY Snapshots®
of the sides and angles of
parallelograms.
Vocabulary
• parallelogram
Large companies have increased using the
Internet to attract and hire employees
• Recognize and apply properties of
the diagonals of parallelograms.
More than three-quarters of Global 5001 companies use
their Web sites to recruit potential employees:
are parallelograms
used to represent
data?
29%
1998
60%
79%
1999
2000
The graphic shows the percent
of Global 500 companies that use the
Internet to find potential employees.
The top surfaces of the wedges of
cheese are all polygons with a similar
shape. However, the size of the
polygon changes to reflect the data.
What polygon is this?
1 — Largest companies in the world, by gross revenue
Source: recruitsoft.com/iLogos Research
By Darryl Haralson and Marcy E. Mullins, USA TODAY
SIDES AND ANGLES OF PARALLELOGRAMS
A quadrilateral with
parallel opposite sides is called a parallelogram.
Study Tip
Parallelogram
Reading Math
Recall that the matching
arrow marks on the
segments mean that the
sides are parallel.
• Words
A parallelogram is a
quadrilateral with both pairs
of opposite sides parallel.
A
D
• Example
B
C08-026C
• Symbols ABCD
There are two pairs
of parallel sides.
AB and DC
AD and BC
C
1 Focus
5-Minute Check
Transparency 8-2 Use as a
quiz or review of Lesson 8-1.
Mathematical Background notes
are available for this lesson on
p. 402C.
are parallelograms used
to represent data?
Ask students:
• Why are parallelograms the
shape used in this graphic?
A wedge can be sliced into
parallelograms.
• Why use cheese in this graphic?
Sample answer: A “mouse” likes
cheese.
• How would you describe the
increase in Internet use to
attract and hire employees in
these companies? Sample
answer: it has more than doubled
from 1998 to 2000.
This activity will help you make conjectures about the sides and angles of a
parallelogram.
Properties of Parallelograms
Make a model
Step 1
G
Draw two sets of intersecting parallel lines
on patty paper. Label the vertices FGHJ.
H
F
J
(continued on the next page)
Lesson 8-2 Parallelograms 411
Resource Manager
Workbook and Reproducible Masters
Chapter 8 Resource Masters
• Study Guide and Intervention, pp. 423–424
• Skills Practice, p. 425
• Practice, p. 426
• Reading to Learn Mathematics, p. 427
• Enrichment, p. 428
• Assessment, p. 473
Prerequisite Skills Workbook, pp. 81–82
Teaching Geometry With Manipulatives
Masters, pp. 8, 129
Transparencies
5-Minute Check Transparency 8-2
Answer Key Transparencies
Technology
Interactive Chalkboard
Lesson x-x Lesson Title 411
2 Teach
Step 2 Trace FGHJ. Label the second parallelogram
PQRS so F and P are congruent.
SIDES AND ANGLES OF
PARALLELOGRAMS
Step 3 Rotate PQRS on FGHJ to compare
sides and angles.
In-Class Example
Analyze
Power
Point®
1 Prove that if a parallelogram
has two consecutive sides
congruent, it has four sides
congruent.
A
D
B
C
Q
R
P
S
1. List all of the segments that are congruent.
2. List all of the angles that are congruent.
3. Describe the angle relationships you observed.
1. FG
HJ PQ
RS, FJ GH
PS Q
R
2. F P H R , J
G Q S
3. Opposite angles
are congruent;
consecutive angles
are supplementary.
The Geometry Activity leads to four properties of parallelograms.
Properties of Parallelograms
Theorem
AB
Given: ABCD; AD
Prove: AD
AB
BC
CD
Statements (Reasons)
1. ABCD (Given)
2. AD
AB
(Given)
3. CD
AB
, BC
AD
(Opposite
sides of a are .)
4. AD
AB
BC
CD
(Transitive property)
8.3
8.4
Opposite sides of a parallelogram
are congruent.
Abbreviation: Opp. sides of are .
A
B
D
C
A
D
B
C
Opposite angles in a
A C
B D
parallelogram are congruent.
Abbreviation: Opp. of are .
8.5
Consecutive angles in a
parallelogram are supplementary.
Abbreviation: Cons. in are suppl.
8.6
Example
If a parallelogram has one right
angle, it has four right angles.
Abbreviation: If has 1 rt. , it has
4 rt. .
A
B
mA mB 180
mB mC 180
mC mD 180
mD mA 180
D
mG 90
mH 90
mJ 90
mK 90
H
J
G
K
C
You will prove Theorems 8.3, 8.5, and 8.6 in Exercises 41, 42, and 43, respectively.
Study Tip
Example 1 Proof of Theorem 8.4
Including
a Figure
Theorems are presented
in general terms. In a
proof, you must include a
drawing so that you can
refer to segments and
angles specifically.
A
B
Write a two-column proof of Theorem 8.4.
Given: ABCD
Prove: A C
D B
D
C
Proof:
Statements
Reasons
1. ABCD
1. Given
DC
BC
2. A
2. Definition of parallelogram
B
㛳 , A
D
㛳
3. A and D are supplementary.
3. If parallel lines are cut by a
D and C are supplementary.
transversal, consecutive interior
C and B are supplementary.
angles are supplementary.
4. A C
4. Supplements of the same angles
D B
are congruent.
412 Chapter 8 Quadrilaterals
Geometry Activity
Materials: ruler
Ask students to recall what they know about the angles formed by parallel lines
and transversals before you do this activity.
412
Chapter 8 Quadrilaterals
Example 2 Properties of Parallelograms
In-Class Example
ALGEBRA Quadrilateral LMNP is a parallelogram.
Find mPLM, mLMN, and d.
mMNP 66 42 or 108 Angle Addition Theorem
PLM MNP
mPLM mMNP
mPLM 108
L
M
LM 2d d
P
N
PN
22
11
M
2d
2 RSTU is a parallelogram.
L
Find mURT, mRST, and y.
66˚
Opp. of are .
Definition of congruent angles
Substitution
mPLM mLMN 180
108 mLMN 180
mLMN 72
Power
Point®
42˚
3y
R
N
S
22
P
Cons. of are suppl.
Substitution
Subtract 108 from each side.
U
18
18
40
T
40; 122, 6
Opp. sides of are .
Definition of congruent segments
Substitution
Substitution
Building on Prior
Knowledge
DIAGONALS OF PARALLELOGRAMS
J
In parallelogram JKLM, JL
and K
M
are diagonals.
Theorem 8.7 states the relationship between
diagonals of a parallelogram.
K
M
L
Theorem 8.7
The diagonals of a parallelogram bisect each other.
R
S
Abbreviation: Diag. of bisect each other.
Q
In Chapter 3, students learned that
if two parallel lines are cut by a
transversal, the alternate interior
angles are congruent. In this
lesson, emphasize that the
diagonals of a parallelogram are
transversals, and therefore the
alternate interior angles are
congruent.
Example: RQ
QT
QU
and SQ
U
T
DIAGONALS OF
PARALLELOGRAMS
You will prove Theorem 8.7 in Exercise 44.
Teaching Tip
Standardized Example 3 Diagonals of a Parallelogram
Test Practice
Multiple-Choice Test Item
What are the coordinates of the intersection of the diagonals of parallelogram
ABCD with vertices A(2, 5), B(6, 6), C(4, 0), and D(0, 1)?
A
Test-Taking Tip
Check Answers Always
check your answer. To check
the answer to this problem,
find the coordinates of the
midpoint of BD
.
(4, 2)
(4.5, 2)
B
C
76, 25 D
(3, 2.5)
Read the Test Item
Since the diagonals of a parallelogram bisect each other, the intersection point is
the midpoint of AC
and B
D
.
x x
y y
Midpoint Formula
(3, 2.5)
The coordinates of the intersection of the diagonals of parallelogram ABCD are
(3, 2.5). The answer is D.
www.geometryonline.com/extra_examples
In-Class Example
Power
Point®
3 What are the coordinates of
the intersection of the
diagonals of parallelogram
MNPR, with vertices
M(3, 0), N(1, 3), P(5, 4),
and R(3, 1)? C
Solve the Test Item
Find the midpoint of AC
.
24 50
1
2
1
2
,
, 2
2 2
2
Make sure students
understand that if diagonals bisect
each other, it implies that they have
the same midpoint. It does not
imply that all four segments created
by the intersection of the diagonals
are congruent.
A (2, 4)
C (1, 2)
92 52 3
D 2, 2
B , Lesson 8-2 Parallelograms 413
Differentiated Instruction
Visual/Spatial Stress that in some parallelograms, the diagonals appear
to bisect the opposite angles, but this is not a property of parallelograms.
Caution students not to assume that angles are bisected. In Lesson 8-5,
students will study rhombi and squares. The diagonals do bisect the
opposite angles in these parallelograms.
Lesson 8-2 Parallelograms 413
Theorem 8.8 describes another characteristic of the diagonals of a parallelogram.
3 Practice/Apply
Theorem 8.8
Each diagonal of a parallelogram separates the
parallelogram into two congruent triangles.
Example: ACD CAB
Concept Check
Odd/Even Assignments
Exercises 16–47 are structured
so that students practice the
same concepts whether they
are assigned odd or even
problems.
1. Describe the characteristics of the sides and angles of a parallelogram.
3. OPEN ENDED Draw a parallelogram with one side twice as long
as another side. 1–3. See margin.
Exercises
Examples
4–12
13–14
15
2
1
3
R
Complete each statement about QRST.
Justify your answer.
V ? V
4. S
Q
; Diag. of bisect each other.
5. VRS 5. VTQ, SSS; diag.
bisect each other
and opp. sides of
are .
Use JKLM to find each measure or value if
JK 2b 3 and JM 3a.
8. mJML 80
7. mMJK 100
9. mJKL 80
T
2b 3
J
K
R
3a
21
10. mKJL 30
11. a 7
30˚
45
M
12. b 21
70˚
L
PROOF
Write the indicated type of proof. 13–14. See p. 459A.
13. two-column
14. paragraph
Given: VZRQ and WQST
Prove: Z T
Q
R
Given: XYRZ, W
Z
W
S
Prove: XYR S
W
S
W
X
Y
T
V
Standardized
Test Practice
414 Chapter 8 Quadrilaterals
3. Sample answer:
x
2x
Z
Z
R
S
15. MULTIPLE CHOICE Find the coordinates of the intersection of the diagonals of
parallelogram GHJK with vertices G(3, 4), H(1, 1), J(3, 5), and K(1, 2). C
A
414 Chapter 8 Quadrilaterals
Q
? .
STQ and SRQ; Consec. in are suppl.
Basic: 17–33 odd, 37–47 odd,
48–63
Average: 17–47 odd, 48–63
Advanced: 16–46 even, 48–60
(optional: 61–63)
1. Opposite sides are congruent;
opposite angles are congruent;
consecutive angles are
supplementary; and if there is
one right angle, there are four
right angles.
2. Diagonals bisect each other; each
diagonal forms two congruent
triangles.
S
V
?
6. TSR is supplementary to
Assignment Guide
Answers
C
2. Describe the properties of the diagonals of a parallelogram.
GUIDED PRACTICE KEY
Organization by Objective
• Sides and Angles of
Parallelograms: 16–33, 41–47
• Diagonals of Parallelograms:
34–40
D
You will prove Theorem 8.8 in Exercise 45.
Guided Practice
About the Exercises…
B
Abbreviation: Diag. separates into 2 s.
Study Notebook
Have students—
• add the definitions/examples of
the vocabulary terms to their
Vocabulary Builder worksheets for
Chapter 8.
• include the parallelogram
theorems studied in this lesson.
• include any other item(s) that they
find helpful in mastering the skills
in this lesson.
A
(0, 0.5)
B
(6, 1)
C
(0, 0.5)
D
(5, 0)
★ indicates increased difficulty
NAME ______________________________________________ DATE
Practice and Apply
16–33
34–40
41–47
2
3
1
A
B
Sides and Angles of Parallelograms A quadrilateral with
both pairs of opposite sides parallel is a parallelogram. Here are four
important properties of parallelograms.
G
D
See page 769.
C
The opposite sides of a
parallelogram are congruent.
Q
SR
and P
S
Q
R
P
The opposite angles of a
parallelogram are congruent.
P R and S Q
The consecutive angles of a
parallelogram are supplementary.
P and S are supplementary; S and R are supplementary;
R and Q are supplementary; Q and P are supplementary.
If a parallelogram has one right
angle, then it has four right angles.
If mP 90, then mQ 90, mR 90, and mS 90.
Example
If ABCD is a parallelogram, find a and b.
AB
and C
D
are opposite sides, so AB
CD
.
2a 34
a 17
DRAWING For Exercises 32 and 33, use the following information.
The frame of a pantograph is a parallelogram.
C
Exercises
Find x and y in each parallelogram.
1.
2.
3x 8y
6x x 30; y 22.5
3.
1
1
33. Find y and FH if HJ y 2 and JF y .
2
2
6x
88
x 15; y 11
4.
3y
x 2; y 4
y 5, FH 9
5.
6.
60
2y
30x
2y 34. DESIGN The chest of drawers shown at the right
is called Side 2. It was designed by Shiro Kuramata.
Describe the properties of parallelograms the artist
used to place each drawer pull.
150
72x
x 13; y 32.5
Gl
12x x 10; y 40
5x 55
3y 6x 12
x 5; y 180
NAME
______________________________________________
DATE
/M
G
Hill
423
Skills
Practice,
8-2
Practice
(Average)
____________
Gl PERIOD
G _____
p. 425 and
Practice,
p. 426 (shown)
Parallelograms
Complete each statement about LMNP. Justify your answer.
★ 35. ALGEBRA Parallelogram ABCD has diagonals
1. L
Q
C and D
A
B
that intersect at point P. If AP 3a 18,
AC 12a, PB a 2b, and PD 3b 1, find a, b,
and DB. a 6, b 5, DB 32
G
?
NPL; opp. of are .
3. LMP ?
NPM; diag. of separates into 2 s.
The pantograph was
used as a primitive copy
machine. The device
makes an exact replica
as the user traces over
a figure.
? . MNP or PLM; cons. in are suppl.
ALGEBRA Use RSTU to find each measure or value.
6. mRST 125
Source: www.infoplease.com
COORDINATE GEOMETRY For Exercises 37–39,
refer to EFGH.
37. Use the Distance Formula to verify that the
diagonals bisect each other.
38. Determine whether the diagonals of this
parallelogram are congruent. no
39. Find the slopes of E
H
and E
F. Are the
consecutive sides perpendicular? Explain.
7. mSTU 9. b R
S
25
B
30
4b 1
55
23
U
6
T
E y
COORDINATE GEOMETRY Find the coordinates of the intersection of the
F
diagonals of parallelogram PRYZ given each set of vertices.
10. P(2, 5), R(3, 3), Y(2, 3), Z(3, 1)
11. P(2, 3), R(1, 2), Y(5, 7), Z(4, 2)
(1.5, 2)
(0, 1)
Q
x
O
12. PROOF Write a paragraph proof of the following.
Given: PRST and PQVU
Prove: V S
G
40. Determine the relationship among
ACBX, ABYC, and ABCZ if XYZ
is equilateral and A, B, and C are
midpoints of X
Z
, X
Y
, and Z
Y
,
respectively. See p. 459A.
slopes of the sides
are not negative
reciprocals of each
other.
Write the indicated type of proof. 41–45. See p. 459A.
41. two-column proof of Theorem 8.3
42. two-column proof of Theorem 8.5
43. paragraph proof of Theorem 8.6
44. paragraph proof of Theorem 8.7
45. two-column proof of Theorem 8.8
R
V
T
13. CONSTRUCTION Mr. Rodriquez used the parallelogram at the right to
design a herringbone pattern for a paving stone. He will use the paving
stone for a sidewalk. If m1 is 130, find m2, m3, and m4.
Y
Q
P
U
Proof: We are given PRST and PQVU. Since opposite
angles of a parallelogram are congruent, P V and
P S. Since congruence of angles is transitive,
V S by the Transitive Property of Congruence.
H
37. EQ 5, QG 5,
HQ 13
,
QF 13
39. Slope of EH
is
undefined, slope of
1
EF ; no, the
S
1
4
2
3
50, 130, 50
B
C
Gl
NAME
______________________________________________
DATE
/M
G
Hill
426
____________
Gl PERIOD
G _____
Reading
8-2
Readingto
to Learn
Learn Mathematics
Mathematics,
p. 427
Parallelograms
X
N
P
N
; opp. sides of are .
?
8. mTUR 125
Drawing
M
Q
P
2. LMN 5. L
M
mBAC 2y, mB 120, mCAD 21, and
CD 21. Find x and y. x 8, y 19.5
L
Q
N
; diag. of bisect each other.
?
4. NPL is supplementary to
★ 36. ALGEBRA In parallelogram ABCD, AB 2x 5,
H
B
112
34
A and C are opposite angles, so A C.
8b 112
b 14
32. Find x and EG if EJ 2x 1 and JG 3x. x 1, EG 6
F
J
2a
A 8b
D
4y 34. Since the
diagonals of a
bisect each other,
the drawer pulls are
at the intersection
point of the diagonals.
E
Q
R
If PQRS is a parallelogram, then
ALGEBRA Use MNPR to find each measure or value.
3x 4
M
N
23. mNRP 33
22. mMNP 71
4w 3 33˚
15.4
24. mRNP 38
25. mRMN 109
17.9
Q 83˚
2y 5
26. mMQN 97
27. mMQR 83
38˚ 3z 3 11.1
28. x 8
29. y 6.45
R
P
20
30. w 3.5
31. z 6.1
Extra Practice
P
S
Lesson 8-2
See
Examples
p. 423
(shown) and p. 424
Parallelograms
Complete each statement about ABCD.
Justify your answer. 16–21. See margin for justifications.
16. DAB ? BCD 17. ABD ? CDB
18. A
B ? D
19. B
G ? G
C
D
20. ABD ? CDB 21. ACD ? BAC
A
Z
Pre-Activity
ELL
How are parallelograms used to represent data?
Read the introduction to Lesson 8-2 at the top of page 411 in your textbook.
3
• What is the name of the shape of the top surface of each wedge of cheese?
parallelogram
PROOF
www.geometryonline.com/self_check_quiz
Lesson 8-2 Parallelograms 415
(l)Pictures Unlimited, (r)Museum of Modern Art/Licensed by SCALA/Art Resource, NY
• Are the three polygons shown in the drawing similar polygons? Explain your
reasoning. No; sample answer: Their sides are not proportional.
Reading the Lesson
1. Underline words or phrases that can complete the following sentences to make statements
that are always true. (There may be more than one correct choice for some of the sentences.)
a. Opposite sides of a parallelogram are (congruent/perpendicular/parallel).
b. Consecutive angles of a parallelogram are (complementary/supplementary/congruent).
c. A diagonal of a parallelogram divides the parallelogram into two
(acute/right/obtuse/congruent) triangles.
d. Opposite angles of a parallelogram are (complementary/supplementary/congruent).
e. The diagonals of a parallelogram (bisect each other/are perpendicular/are congruent).
f. If a parallelogram has one right angle, then all of its other angles are
(acute/right/obtuse) angles.
NAME ______________________________________________ DATE
Answers
16. Opp. of are .
17. Alt. int. are .
18. Opp. sides of are ||.
19. Diag. of bisect each other.
20. Diag. of separates into 2 s.
21. Alt. int. are .
8-2
Enrichment
Enrichment,
____________ PERIOD _____
p. 428
2. Let ABCD be a parallelogram with AB BC and with no right angles.
a. Sketch a parallelogram that matches the description
above and draw diagonal BD
.
Sample answer:
In parts b–f, complete each sentence.
A
Tessellations
B
||
b. A
A tessellation is a tiling pattern made of polygons. The pattern can
be extended so that the polygonal tiles cover the plane completely with
no gaps. A checkerboard and a honeycomb pattern are examples of
tessellations. Sometimes the same polygon can make more than one
tessellation pattern. Both patterns below can be formed from an
isosceles triangle.
B
c. A
D
C
D
and B
C
B A
d. A C
and ABC CDA .
D
C
and A
D
||
C
B
.
angles formed by the two parallel lines
BD
C
D
.
e. ADB CBD because these two angles are
transversal
B
AD
alternate
interior
and the
BC
and
.
f. ABD CDB .
Helping You Remember
3. A good way to remember new theorems in geometry is to relate them to theorems you
learned earlier. Name a theorem about parallel lines that can be used to remember the
theorem that says, “If a parallelogram has one right angle, it has four right angles.”
Perpendicular Transversal Theorem
D
t
ll ti
i
h
l
Lesson 8-2 Parallelograms 415
Lesson 8-2
For
Exercises
____________ PERIOD _____
Study
Guide
andIntervention
Intervention,
8-2
Study
Guide and
PROOF
Write a two-column proof. 46– 47. See margin.
46. Given: DGHK, FH
GD
DJ HK
HD
FD
, 47. Given: BCGH, Prove: DJK HFG
Prove: F GCB
4 Assess
Open-Ended Assessment
G
F
D
H
B
Writing Ask students to list all
the properties of parallelograms
they have learned.
G
H
J
K
D
48. CRITICAL THINKING Find the ratio of MS to SP, given
1
1
that MNPQ is a parallelogram with MR MN. 4
2
Getting Ready for
Lesson 8-3
Prerequisite Skill Students will
learn about the tests for
parallelograms in Lesson 8-3.
They will use slope to prove that
opposite sides of a quadrilateral
are parallel. Use Exercises 61–63
to determine your students’
familiarity with finding slope.
C
F
M
R
N
S
Q
T
P
Answer the question that was posed at the beginning of
the lesson. See margin.
How are parallelograms used to represent data?
49. WRITING IN MATH
Include the following in your answer:
• properties of parallelograms, and
• a display of the data in the graphic with a different parallelogram.
Standardized
Test Practice
Assessment Options
50. SHORT RESPONSE Two consecutive angles of a parallelogram measure
(3x 42)° and (9x 18)°. Find the measures of the angles. 81, 99
51. ALGEBRA The perimeter of the rectangle ABCD is equal
y
to p and x . What is the value of y in terms of p? B
Quiz (Lessons 8-1 and 8-2) is
available on p. 473 of the Chapter 8
Resource Masters.
A
p
3
5
B
5p
12
C
5p
8
D
5p
6
A
y
x
D
B
x
y
C
Maintain Your Skills
Mixed Review
(Lesson 8-1)
46. Given: DGHK is a parallelogram.
FH
⊥
GD
J ⊥ D
HK
Prove: DJK HFG
G F
H
D
J K
Proof:
Statements (Reasons)
1. DGHK is a parallelogram;
FH
⊥
GD
, DJ ⊥ HK
. (Given)
2. G K (Opp. of .)
3. GH
DK
(Opp. sides of .)
4. HFG and DJK are rt. .
(⊥ lines form four rt. .)
5. HFG and DJK are rt. s.
(Def. of rt. s)
6. HFG DJK (HA)
47. Given: BCGH,
H
B
HD
FD
G
Prove: F GCB
D
F
Proof:
C
Statements (Reasons)
1. BCGH, HD
FD
(Given)
2. F H (Isosceles Thm.)
3. H GCB (Opp. of .)
4. F GCB (Congruence of is transitive.)
416 Chapter 8 Quadrilaterals
Find the sum of the measures of the interior angles of each convex polygon.
52. 14-gon 2160
53. 22-gon 3600
54. 17-gon 2700
55. 36-gon 6120
Determine whether the Law of Sines or the Law of Cosines should be used
to solve each triangle. Then solve each triangle. Round to the nearest tenth.
(Lesson 7-7)
A
C
57. B
58.
14
56. Cosines; a 8.8, 56.
A
57˚
mB 56.8, mC 78˚ 24
21
42˚
81.2
13
a
A
12.5
11
c
57. Sines; mC B
69.9, mA 53.1,
C
B
a
a 11.9
C
58. Cosines; c 28.4,
Use Pascal’s Triangle for Exercises 59 and 60. (Lesson 6-6) 59. 30
mA 46.3, mB 59. Find the sum of the first 30 numbers in the outside diagonal of Pascal’s triangle.
55.7
60. Find the sum of the first 70 numbers in the second diagonal. 2485
Getting Ready for
the Next Lesson
PREREQUISITE SKILL The vertices of a quadrilateral are A(5, 2),
B(2, 5), C(2, 2), and D(1, 9). Determine whether each segment is a
side or a diagonal of the quadrilateral, and find the slope of each segment.
(To review slope, see Lesson 3-3.)
7
61. A
B
side, 3
62. B
D
diagonal, 14
416 Chapter 8 Quadrilaterals
49. Sample answer: The graphic uses the
illustration of wedges shaped like
parallelograms to display the data.
Answers should include the following.
• The opposite sides are parallel and
congruent, the opposite angles are
congruent, and the consecutive
angles are supplementary.
• Sample answer:
100
Percent That
Use the Web
Answers
79%
80
60%
60
40 29%
20
0
1998 1999 2000
Year
7
63. C
D
side, 3
Lesson
Notes
Tests for Parallelograms
• Recognize the conditions that ensure a
1 Focus
quadrilateral is a parallelogram.
• Prove that a set of points forms a
parallelogram in the coordinate plane.
5-Minute Check
Transparency 8-3 Use as a
quiz or review of Lesson 8-2.
are parallelograms
used in architecture?
The roof of the covered bridge
appears to be a parallelogram. Each
pair of opposite sides looks like they
are the same length. How can we
know for sure if this shape is really
a parallelogram?
Mathematical Background notes
are available for this lesson on
p. 402C.
CONDITIONS FOR A PARALLELOGRAM By definition, the opposite sides
of a parallelogram are parallel. So, if a quadrilateral has each pair of opposite sides
parallel it is a parallelogram. Other tests can be used to determine if a quadrilateral
is a parallelogram.
Testing for a Parallelogram
Model
• Cut two straws to one length and two other
straws to a different length.
• Connect the straws by inserting a pipe cleaner
in one end of each size of straw to form a
quadrilateral like the one shown at the right.
• Shift the sides to form quadrilaterals of
different shapes.
are parallelograms used
in architecture?
Ask students:
• Which geometric shape is used
most often in the construction of
the roof of a house? parallelogram
• Why is this shape used for
roofs? Sample answer: It is easy
to build or construct.
• What is another structure that
uses this shape in its
construction? Sample answer:
doors and doorways
Analyze
4. Opposite angles are
congruent, and
consecutive angles
are supplementary.
5. Opposite sides are
parallel and
congruent, opposite
angles are congruent,
or consecutive angles
are supplementary.
1. Measure the distance between the opposite sides of the quadrilateral in
at least three places. Repeat this process for several figures. What can you
conclude about opposite sides? They appear to be parallel.
2. Classify the quadrilaterals that you formed. parallelograms
3. Compare the measures of pairs of opposite sides. They are equal.
4. Measure the four angles in several of the quadrilaterals. What relationships
do you find?
Make a Conjecture
5. What conditions are necessary to verify that a quadrilateral is a
parallelogram?
Lesson 8-3 Tests for Parallelograms 417
Neil Rabinowitz/CORBIS
Resource Manager
Workbook and Reproducible Masters
Chapter 8 Resource Masters
• Study Guide and Intervention, pp. 429–430
• Skills Practice, p. 431
• Practice, p. 432
• Reading to Learn Mathematics, p. 433
• Enrichment, p. 434
School-to-Career Masters, p. 15
Teaching Geometry With Manipulatives
Masters, pp. 2, 16, 130, 132
Transparencies
5-Minute Check Transparency 8-3
Answer Key Transparencies
Technology
Interactive Chalkboard
Lesson x-x Lesson Title 417
Proving Parallelograms
2 Teach
Theorem
CONDITIONS FOR A
PARALLELOGRAM
Teaching Tip
Note that Theorems
8.9, 8.10, and 8.11 are converses of
the theorems in Lesson 8-2.
In-Class Examples
8.9
If both pairs of opposite sides of a quadrilateral are congruent, then the
quadrilateral is a parallelogram.
Abbreviation: If both pairs of opp. sides are , then quad. is .
8.10
If both pairs of opposite angles of a quadrilateral are congruent, then the
quadrilateral is a parallelogram.
Abbreviation: If both pairs of opp. are , then quad. is .
8.11
If the diagonals of a quadrilateral bisect each other, then the quadrilateral
is a parallelogram.
Abbreviation: If diag. bisect each other, then quad. is .
8.12
If one pair of opposite sides of a quadrilateral is both parallel and
congruent, then the quadrilateral is a parallelogram.
Abbreviation: If one pair of opp. sides is and , then the quad. is a .
Power
Point®
Teaching Tip
Emphasize that
the theorems on this page are
used in proofs. In this lesson,
students learn that to prove that
a quadrilateral is a parallelogram,
they must establish that one of
these theorems applies to the
quadrilateral.
You will prove Theorems 8.9, 8.11, and 8.12 in Exercises 39, 40, and 41, respectively.
Example 1 Write a Proof
PROOF
1 Write a paragraph proof of
A
Paragraph Proof:
Bavarian crest appear to be
parallelograms. Describe the
information needed to
determine whether the shapes
are parallelograms.
A
Likewise, 2mA 2mD 360, or mA mD 180. These consecutive
DC
supplementary angles verify that AB
. Opposite sides are parallel, so
ABCD is a parallelogram.
Art
Ellsworth Kelly created
Sculpture for a Large Wall
in 1957. The sculpture is
made of 104 aluminum
panels. The piece is over
65 feet long, 11 feet high,
and 2 feet deep.
Example 2 Properties of Parallelograms
ART Some panels in the sculpture appear to be parallelograms. Describe the
information needed to determine whether these panels are parallelograms.
Source: www.moma.org
A panel is a parallelogram if both pairs of opposite sides are congruent, or if one
pair of opposite sides is congruent and parallel. If the diagonals bisect each other,
or if both pairs of opposite angles are congruent, then the panel is a parallelogram.
Chapter 8 Quadrilaterals
(l)Richard Schulman/CORBIS, (r)Museum of Modern Art/Licensed by SCALA/Art Resource, NY
418
Chapter 8 Quadrilaterals
D
Since A C and B D, mA mC and mB mD. Substitute to
find that mA mA mB mB 360, or 2(mA) 2(mB) 360.
Dividing each side of the equation by 2 yields mA mB 180. This means
BC
.
that consecutive angles are supplementary and AD
418
If both pairs of opposite sides are
the same length or if one pair of
opposite sides is congruent and
parallel, the quadrilateral is a
parallelogram. If both pairs of
opposite angles are congruent or
if the diagonals bisect each
other, the quadrilateral is a
parallelogram.
C
. We now have two triangles.
Because two points determine a line, we can draw AC
We know the sum of the angle measures of a triangle is 180, so the sum of the angle
measures of two triangles is 360. Therefore, mA mB mC mD 360.
D
2 Some of the shapes in this
B
Prove: ABCD is a parallelogram.
C
Given: ABD CDB
Prove: ABCD is a
parallelogram.
Since ABD CDB, AB
CD
,
and B
C
DA
by CPCTC.
Therefore ABCD is a parallelogram
because if a quadrilateral has
both pairs of opposite sides
congruent, it is a parallelogram.
Write a paragraph proof for Theorem 8.10
Given: A C, B D
the statement: If a diagonal of
a quadrilateral divides the
quadrilateral into two congruent
triangles, then the quadrilateral
is a parallelogram.
B
Example
Geometry Activity
Materials: straws, scissors, pipe cleaners, protractors
You may want to do this activity in groups of four students. Ask one student
to cut the straws. Ask a second student in the group to construct the
parallelogram and a third student to measure the opposite sides. Ask the
fourth student to measure the opposite angles. Then ask students to rotate
roles and repeat the activity with different length straws.
Building on Prior
Knowledge
Example 3 Properties of Parallelograms
Determine whether the quadrilateral is a
parallelogram. Justify your answer.
Each pair of opposite angles have the same
measure. Therefore, they are congruent. If both
pairs of opposite angles are congruent, the
quadrilateral is a parallelogram.
115˚
65˚
65˚
115˚
A quadrilateral is a parallelogram if any one of the following is true.
Tests for a Parallelogram
1. Both pairs of opposite sides are parallel. (Definition)
In Lesson 3-3, students learned
how to find the slope of parallel
lines. In this lesson, they will use
slope to show that a quadrilateral
in the coordinate plane is or is
not a parallelogram.
In-Class Examples
3 Determine whether the
2. Both pairs of opposite sides are congruent. (Theorem 8.9)
quadrilateral is a
parallelogram. Justify your
answer.
3. Both pairs of opposite angles are congruent. (Theorem 8.10)
4. Diagonals bisect each other. (Theorem 8.11)
35
5. A pair of opposite sides is both parallel and congruent. (Theorem 8.12)
20
Study Tip
Common
Misconceptions
If a quadrilateral meets
one of the five tests, it
is a parallelogram. All
of the properties of
parallelograms need
not be shown.
Each pair of opposite sides have
the same measure. Therefore,
they are congruent. If both pairs
of opposite sides are congruent,
the quadrilateral is a
parallelogram.
ALGEBRA Find x and y so that each quadrilateral is a parallelogram.
a.
4y
E
F
2x 36
6y 42
D
G
Opposite sides of a parallelogram are congruent.
E
D
F
G
D
G
Opp. sides of are .
EF
DE FG
EF DG
Def. of segments
6x 12 2x 36
4y 6y 42 Substitution
4x 48
2y 42
Subtract 6y.
x 12
y 21
Divide by 2.
So, when x is 12 and y is 21, DEFG is a parallelogram.
b.
R
x
2y 12
Opp. sides of
are .
4 Find x and y so that each
quadrilateral is a
parallelogram.
Def. of segments
Substitution
Subtract 2x and add 12.
a.
4x 1
Divide by 4.
3(x 2)
S
x7
T
b.
5y
Q
20
35
Example 4 Find Measures
6x 12
(5y 28)
5x 28 P
(6y 14)
Diagonals in a parallelogram bisect each other.
QT
T
S
QT TS
5y 2y 12
3y 12
y4
Power
Point®
Opp. sides of
are .
Def. of segments
Substitution
Subtract 2y.
Divide by 3.
RT
T
P
RT TP
x 5x 28
4x 28
x7
Opp. sides of
are .
y 14
Def. of segments
Substitution
Subtract 5x.
Divide by 4.
PQRS is a parallelogram when x 7 and y 4.
www.geometryonline.com/extra_examples
Lesson 8-3 Tests for Parallelograms 419
Differentiated Instruction
Intrapersonal Have students choose a partner. Ask one student to draw
a parallelogram in the plane. Then ask the partner to prove that the
quadrilateral is a parallelogram. Next switch roles and do the activity again.
Lesson 8-3 Tests for Parallelograms 419
PARALLELOGRAMS ON THE COORDINATE PLANE We can use the
Distance Formula and the Slope Formula to determine if a quadrilateral is a
parallelogram in the coordinate plane.
PARALLELOGRAMS ON
THE COORDINATE PLANE
In-Class Example
Power
Point®
5 COORDINATE GEOMETRY
Determine whether the figure
with the given vertices is a
parallelogram. Use the
method indicated.
Study Tip
Example 5 Use Slope and Distance
Coordinate
Geometry
COORDINATE GEOMETRY Determine whether the figure with the given
vertices is a parallelogram. Use the method indicated.
a. A(3, 3), B(8, 2), C(6, 1), D(1, 0); Slope Formula
y
If the opposite sides of a quadrilateral are parallel,
A
then it is a parallelogram.
The Midpoint Formula
can also be used to
show that a
quadrilateral is a
parallelogram by
Theorem 8.11.
2 3 1
1 0 1
or slope of DC
or slope of AB
83
5
61
5
30 3
3
1 2
slope of AD
or slope of BC
or 68
31 2
2
a. A(3, 0), B(1, 3), C(3, 2),
D(1, 1); Slope Formula
y
C(3, 2)
x
D(1, –1)
(
2)]2 (3 7
)2
PS [5
3
2
Slope of A
B ; slope of C
D ;
8 64 2O
R
(1)]2
72 (
4)2 or 65
the same slope, A
B
|| C
D
and
||
AD
B
C
. Therefore, ABCD is a
parallelogram.
P
2 4 6 8x
4
6 Q
8
QR [1 [5 (6)]2
y
4
2
72 (
4)2 or 65
1
slope of A
D ; slope of B
C
4
1
. Since opposite sides have
4
Since PS QR, PS
Q
R
.
Next, use the Slope Formula to determine whether P
QR
S
.
b. P(3, 1), Q(1, 3), R(3, 1),
S(1, 3); Distance and Slope
Formulas
37
5 (2)
4
7
or slope of PS
5 (1)
1 (6)
4
7
slope of Q
R
or S
P
and Q
R
have the same slope, so they are parallel. Since one pair of opposite
sides is congruent and parallel, PQRS is a parallelogram.
y
Q (–1, 3)
C
b. P(5, 3), Q(1, 5), R(6, 1), S(2, 7); Distance and Slope Formulas
First use the Distance Formula to determine whether
S 8
the opposite sides are congruent.
6
O
3
2
x
O D
Since opposite sides have the same slope, AB
and
DC
A
BC
D
. Therefore, ABCD is a parallelogram by definition.
B(–1, 3)
A(–3, 0)
B
R(3, 1)
x
O
Concept Check
P(–3, –1)
2. OPEN ENDED
S(1, –3)
Carter
1
2
P
S
; slope of QR
.
A quadrilateral is a parallelogram
if one pair of opposite sides
is congruent and one pair of
opposite sides is parallel.
Since opposite sides have the
same slope, P
S
|| Q
R
. Since one
pair of opposite sides is congruent
and parallel, PQRS is a
parallelogram.
Answers
420
Chapter 8 Quadrilaterals
Shaniqua
A quadrilateral is a parallelogram
if one pair of opposite sides is
congruent and parallel.
Who is correct? Explain your reasoning. Shaniqua; Carter’s description could
420 Chapter 8 Quadrilaterals
1. Both pairs of opposite sides are
congruent; both pairs of opposite
angles are congruent; diagonals
bisect each other; one pair of
opposite sides is parallel and
congruent.
Draw a parallelogram. Label the congruent angles.
3. FIND THE ERROR Carter and Shaniqua are describing ways to show that a
quadrilateral is a parallelogram.
PS 20; QR 20; therefore
PS QR, and PS
QR
. Slope of
1
2
1. List and describe four tests for parallelograms. 1–2. See margin.
2. Sample answer:
B
A
C
D
result in a shape that is not a parallelogram.
Guided Practice
GUIDED PRACTICE KEY
Exercises
Examples
4–5
6–7
8–10
11
12
3
4
5
1
2
Determine whether each quadrilateral is a parallelogram. Justify your answer.
4.
5. 78˚
No; one pair of
Yes; each
102˚
opp. sides are
not parallel and
congruent.
ALGEBRA
6.
102˚
102˚
Find x and y so that each quadrilateral is a parallelogram.
5y
x 13, y 4
7.
(3x 17)˚
(y 58)˚
2x 5
3x 18
(5y 6)˚
pair of opp.
is .
x 41,
y 16
(2x 24)˚
2y 12
COORDINATE GEOMETRY Determine whether the figure with the given vertices
is a parallelogram. Use the method indicated.
8. B(0, 0), C(4, 1), D(6, 5), E(2, 4); Slope Formula yes
9. A(4, 0), B(3, 1), C(1, 4), D(6, 3); Distance and Slope Formulas yes
10. E(4, 3), F(4, 1), G(2, 3), H(6, 2); Midpoint Formula no
11. PROOF Write a two-column proof to prove that
TR
and
PQRS is a parallelogram given that PT
TSP TQR. See p. 459A–459B.
S
Application
P
Q
T
R
12. TANGRAMS A tangram set consists of seven pieces:
a small square, two small congruent right triangles, two
large congruent right triangles, a medium-sized right
triangle, and a quadrilateral. How can you determine
the shape of the quadrilateral? Explain. See margin.
★ indicates increased difficulty
Practice and Apply
For
Exercises
See
Examples
13–18
19–24
25–36
37–38
39–42
3
4
5
2
1
Determine whether each quadrilateral is a parallelogram. Justify your answer.
yes
14.
yes 15. yes
13.
155˚ 25˚
3
3
25˚
no
16.
yes
17.
155˚
no
18.
3 Practice/Apply
Study Notebook
Have students—
• add the definitions/examples of
the vocabulary terms to their
Vocabulary Builder worksheets for
Chapter 8.
• write the four theorems to prove
that a quadrilateral is a
parallelogram in their notes. Ask
them to include an example of each.
• include any other item(s) that they
find helpful in mastering the skills
in this lesson.
FIND THE ERROR
In Exercise 3,
caution students that
the same pair of opposite sides
needs to be congruent and parallel
in order to use the theorem that
applies. Otherwise the
quadrilateral could be an isosceles
trapezoid (studied in Lesson 8-6).
Extra Practice
See page 769.
13– 18. See margin
for justifications.
19. x 6, y 24
20. x 1, y 9
21. x 1, y 2
ALGEBRA
19.
Find x and y so that each quadrilateral is a parallelogram.
2x 3
3y
20.
21.
y 2x
4y
8y 36
2x
About the Exercises…
5x
5x 18
3y 2x
5y 2x
96 y
4
22. x 4, y 4
23. x 34, y 44
1
24. x 8, y 1
3
22.
25x˚
40˚
★ 23.
(x 12)˚
(3y 4)˚
10y˚
100˚
(4x 8)˚
★ 24.
1
2 y˚
4y
x
3y 4
2
3x
Lesson 8-3 Tests for Parallelograms 421
Odd/Even Assignments
Exercises 13–42 are structured
so that students practice the
same concepts whether they
are assigned odd or even
problems.
Assignment Guide
Answers
12. If one pair of opposite sides are
congruent and parallel, the quadrilateral
is a parallelogram.
13. Each pair of opposite angles is
congruent.
14. The diagonals bisect each other.
15. Opposite angles are congruent.
Organization by Objective
• Conditions for a
Parallelogram: 13–24, 37–42
• Parallelograms on the
Coordinate Plane: 25–36
16. None of the tests for parallelograms are
fulfilled.
17. One pair of opposite sides is parallel and
congruent.
18. None of the tests for parallelograms are
fulfilled.
Basic: 13–21 odd, 25–31 odd,
37–43 odd, 44–63
Average: 13–43 odd, 44–63
Advanced: 14–42 even, 43–59
(optional: 60–63)
All: Quiz 1 (1–5)
Lesson 8-3 Tests for Parallelograms 421
NAME ______________________________________________ DATE
COORDINATE GEOMETRY Determine whether a figure with the given vertices is
a parallelogram. Use the method indicated.
25. B(6, 3), C(2, 3), E(4, 4), G(4, 4); Slope Formula yes
26. Q(3, 6), R(2, 2), S(1, 6), T(5, 2); Slope Formula no
27. A(5, 4), B(3, 2), C(4, 4), D(4, 2); Distance Formula yes
28. W(6, 5), X(1, 4), Y(0, 1), Z(5, 2); Midpoint Formula yes
29. G(2, 8), H(4, 4), J(6, 3), K(1, 7); Distance and Slope Formulas no
30. H(5, 6), J(9, 0), K(8, 5), L(3, 2); Distance Formula no
31. S(1, 9), T(3, 8), V(6, 2), W(2, 3); Midpoint Formula yes
32. C(7, 3), D(3, 2), F(0, 4), G(4, 3); Distance and Slope Formulas yes
____________ PERIOD _____
Study
Guide
andIntervention
Intervention,
8-3
Study
Guide and
p. 429
(shown)
and p. 430
Tests for
Parallelograms
Conditions for a Parallelogram There are many ways to
establish that a quadrilateral is a parallelogram.
A
B
E
D
If:
C
If:
|| D
C
and A
D
|| B
C
,
both pairs of opposite sides are parallel,
A
B
both pairs of opposite sides are congruent,
A
B
DC
and AD
BC
,
both pairs of opposite angles are congruent,
ABC ADC and DAB BCD,
A
E
CE
and D
E
BE
,
the diagonals bisect each other,
A
B
one pair of opposite sides is congruent and parallel,
then: the figure is a parallelogram.
|| C
D
and A
B
, or A
D
|| B
C
and A
D
B
C
,
CD
then: ABCD is a parallelogram.
Example
Find x and y so that FGHJ is a
parallelogram.
FGHJ is a parallelogram if the lengths of the opposite
sides are equal.
4x 2y 4(2) 2y 8 2y 2y y
G
2
J
15
H
2
2
2
6
3
Exercises
Find x and y so that each quadrilateral is a parallelogram.
1.
x 7; y 4
2x 2
2y
2.
5y R(5, 2). Determine how to move one vertex to make MNPR a parallelogram.
Move M to (4, 1), N to (3, 4), P to (0, 9), or R to (7, 3).
★ 34. Quadrilateral QSTW has vertices Q(3, 3), S(4, 1), T(1, 2), and W(5, 1).
8
11x 12
3.
25
5y 5.
x 31; y 5 4.
5x x 5; y 3
18
x 15; y 9
(x y)
2x 9x 45
6.
3x NAME
______________________________________________
DATE
/M
G
Hill
429
Move Q to (0, 2), S to (1, 2), T to (2, 3), or W to (8, 0).
COORDINATE GEOMETRY The coordinates of three of the vertices of a
parallelogram are given. Find the possible coordinates for the fourth vertex.
★ 35. A(1, 4), B(7, 5), and C(4, 1). (2, 2), (4, 10), or (10, 0)
★ 36. Q(2, 2), R(1, 1), and S(1, 1). (2, 2), (4, 0), or (0, 4)
6y
Skills
Practice,
8-3
Practice
(Average)
Determine how to move one vertex to make QSTW a parallelogram.
More About . . .
x 30; y 15
6y 30
24
Gl
x 5; y 25
55
★ 33. Quadrilateral MNPR has vertices M(6, 6), N(1, 1), P(2, 4), and
Lesson 8-3
6x 3 15
6x 12
x2
6x 3
F
4x 2y
____________
Gl PERIOD
G _____
37. STORAGE Songan purchased an expandable
hat rack that has 11 pegs. In the figure, H is the
midpoint of K
M
and JL
. What type of figure is
JKLM? Explain. Parallelogram; KM
and JL are
p. 431 and
Practice,
p. 432 (shown)
Tests for Parallelograms
Determine whether each quadrilateral is a parallelogram. Justify your answer.
1.
2.
Yes; the diagonals bisect
each other.
3.
118
4.
62
62
No; none of the tests for
parallelograms is fulfilled.
118
Yes; both pairs of opposite
angles are congruent.
No; none of the tests for
parallelograms is fulfilled.
COORDINATE GEOMETRY Determine whether a figure with the given vertices is a
parallelogram. Use the method indicated.
Atmospheric
Scientist
diagonals that bisect each other.
no
ALGEBRA Find x and y so that each quadrilateral is a parallelogram.
7.
(5x 29)
(3y 15)
(5y 9)
8.
2x
y
4x 6
x 3, y 2
5
12y 7
7y 3
8
2y 3
x
4
2
x 6, y 13
10.
6x
x
3y x 20, y 12
9.
4
(7x 11)
6
23
2
4y
x
12
For information about
a career as an
atmospheric scientist,
visit:
www.geometryonline.
com/careers
PROOF
Write a two-column proof of each theorem. 39–41. See p. 459B.
39. Theorem 8.9
40. Theorem 8.11
41. Theorem 8.12
★ 42. Li-Cheng claims she invented a new geometry theorem. A diagonal of a
parallelogram bisects its angles. Determine whether this theorem is true. Find an
example or counterexample. See margin.
x 2, y 5
43. CRITICAL THINKING Write a proof to prove that FDCA is a
parallelogram if ABCDEF is a regular hexagon. See margin.
Sample answer: Confirm that both pairs of opposite s are .
NAME
______________________________________________
DATE
/M
G
Hill
432
____________
Gl PERIOD
G _____
Reading
8-3
Readingto
to Learn
Learn Mathematics
Mathematics,
p. 433
Tests for Parallelograms
Pre-Activity
ELL
Answer the question that was posed at
the beginning of the lesson. See margin.
How are parallelograms used in architecture?
44. WRITING IN MATH
How are parallelograms used in architecture?
Read the introduction to Lesson 8-3 at the top of page 417 in your textbook.
Make two observations about the angles in the roof of the covered bridge.
Sample answer: Opposite angles appear congruent.
Consecutive angles appear supplementary.
1. Which of the following conditions guarantee that a quadrilateral is a parallelogram?
B, D, G, H, J, L
2. Determine whether there is enough given information to know that each figure is a
parallelogram. If so, state the definition or theorem that justifies your conclusion.
a.
b.
422
Chapter 8 Quadrilaterals
(l)Aaron Haupt, (r)AFP/CORBIS
NAME ______________________________________________ DATE
8-3
Enrichment
Enrichment,
____________ PERIOD _____
p. 434
Tests for Parallelograms
no
c.
Yes; if the diagonals bisect each
other, then the quadrilateral is a
parallelogram.
d.
Yes; if both pairs of opposite
sides are , then quadrilateral
is .
no
By definition, a quadrilateral is a parallelogram if and only if both pairs of opposite sides
are parallel. What conditions other than both pairs of opposite sides parallel will guarantee
that a quadrilateral is a parallelogram? In this activity, several possibilities will be
investigated by drawing quadrilaterals to satisfy certain conditions. Remember that any
test that seems to work is not guaranteed to work unless it can be formally proven.
Complete.
1. Draw a quadrilateral with one pair of opposite sides congruent.
Must it be a parallelogram? no
Helping You Remember
3. A good way to remember a large number of mathematical ideas is to think of them in
groups. How can you state the conditions as one group about the sides of quadrilaterals
that guarantee that the quadrilateral is a parallelogram? Sample answer: both
pairs of opposite sides parallel, both pairs of opposite sides congruent,
or one pair of opposite sides both parallel and congruent
422
Chapter 8 Quadrilaterals
A
2. Draw a quadrilateral with both pairs of opposite sides congruent.
Must it be a parallelogram? yes
Answers
38. If both pairs of opposite sides are
parallel and congruent, then the
watchbox is a parallelogram.
B
F
C
E
Include the following in your answer:
• the information needed to prove that the roof of the covered bridge is a
parallelogram, and
• another example of parallelograms used in architecture.
Reading the Lesson
A. Two sides are parallel.
B. Both pairs of opposite sides are congruent.
C. The diagonals are perpendicular.
D. A pair of opposite sides is both parallel and congruent.
E. There are two right angles.
F. The sum of the measures of the interior angles is 360.
G. All four sides are congruent.
H. Both pairs of opposite angles are congruent.
I. Two angles are acute and the other two angles are obtuse.
J. The diagonals bisect each other.
K. The diagonals are congruent.
L. All four angles are right angles.
M
Data Update Each hurricane is assigned
a name as the storm develops. What is the name of the most
recent hurricane or tropical storm in the Atlantic or Pacific Oceans?
Visit www.geometryonline.com/data_update to learn more.
11. TILE DESIGN The pattern shown in the figure is to consist of congruent
parallelograms. How can the designer be certain that the shapes are
parallelograms?
Gl
H
L
Online Research
Online Research
yes
J
38. METEOROLOGY To show the center of a storm, television stations superimpose
a “watchbox” over the weather map. Describe how you know that the watchbox
is a parallelogram. See margin.
Atmospheric scientists, or
meteorologists, study
weather patterns. They can
work for private companies,
the Federal Government or
television stations.
5. P(5, 1), S(2, 2), F(1, 3), T(2, 2); Slope Formula
6. R(2, 5), O(1, 3), M(3, 4), Y(6, 2); Distance and Slope Formula
K
D
Standardized
Test Practice
45. A parallelogram has vertices at (2, 2), (1, 6), and (8, 2). Which ordered pair
could represent the fourth vertex? B
A (5, 6)
B (11, 6)
C (14, 3)
D (8, 8)
Open-Ended Assessment
46. ALGEBRA Find the distance between X(5, 7) and Y(3, 4). C
A B 315
C 185
D 529
19
Modeling Ask students to
demonstrate how to “build” a
parallelogram from straws of
various lengths.
Maintain Your Skills
Mixed Review
Use NQRM to find each measure
or value. (Lesson 8-2)
47. w 12
48. x 4
49. NQ 14 units
50. QR 15 units
3x 2
N
Q
12
2y 5
w
L
Getting Ready for
Lesson 8-4
3y
4x 2
M
R
The measure of an interior angle of a regular polygon is given. Find the number
of sides in each polygon. (Lesson 8-1)
51. 135 8
52. 144 10
53. 168 30
54. 162 20
55. 175 72
56. 175.5 80
Find x and y. (Lesson 7-3)
57.
45, 122 58.
y
103
, 30
x
59.
y˚
12
y
32
20
x
60˚
x˚
12
163
, 16
10
Getting Ready for
the Next Lesson
3
2
61. 5, ; not B and BC
PREREQUISITE SKILL Use slope to determine whether A
are
perpendicular or not perpendicular. (To review slope and perpendicularity, see Lesson 3-3.)
60. A(2, 5), B(6, 3), C(8, 7) 1, 2; 61. A(1, 2), B(0, 7), C(4, 1)
2
62. A(0, 4), B(5, 7), C(8, 3)
63. A(2, 5), B(1, 3), C(1, 0)
3
4
2
3
, ; not , ; 5
3
3
2
P ractice Quiz 1
Lessons 8-1 through 8-3
3
1. The measure of an interior angle of a regular polygon is 147.
11
3. mXYZ 42 x
X
(Lesson 8-2)
Y
Answers
A
D
B
54˚
x2
Z
ALGEBRA Find x and y so that each quadrilateral is a parallelogram. (Lesson 8-3)
3y 2
4.
x 14, y 31
5.
x 8, y 6
(6y 57)˚ (5x 19)˚
C
43. Given: ABCDEF is a regular
hexagon.
Prove: FDCA is a parallelogram.
A
x4
2x 4
B
F
4y 8
www.geometryonline.com/self_check_quiz
Practice Quiz 1 The quiz
provides students with a brief
review of the concepts and skills
in Lessons 8-1 through 8-3.
Lesson numbers are given to the
right of the exercises or instruction
lines so students can review
concepts not yet mastered.
P
? . 66
(3y 36)˚
Assessment Options
60˚
W
(3x 9)˚
Prerequisite Skill Students will
learn about rectangles in Lesson
8-4. They will find the slopes of
adjacent sides of a quadrilateral
to determine if they are
perpendicular. Use Exercises 60–63
to determine your students’
familiarity with finding slope.
42. This theorem is not true. ABCD is
a parallelogram with diagonal BD
,
ABD CBD.
Find the number of sides in the polygon. (Lesson 8-1) 11
Use WXYZ to find each measure.
2. WZ ? . 36 or 49
4 Assess
C
E
Lesson 8-3 Tests for Parallelograms 423
44. Sample answer: The roofs of some
covered bridges are parallelograms. The
opposite sides are congruent and parallel.
Answers should include the following.
• We need to know the length of the sides,
or the measures of the angles formed.
• Sample answer: windows or tiles
D
Proof:
Statements (Reasons)
1. ABCDEF is a regular hexagon.
(Given)
2. A
B
DE, B
C
EF, E B,
F
A
C
D (Def. regular hexagon)
3. ABC DEF (SAS)
4. AC
DF (CPCTC}
5. FDCA is a . (If both pairs of
opp. sides are , then the
quad. is a .)
Lesson 8-3 Tests for Parallelograms 423
Lesson
Notes
Rectangles
• Recognize and apply properties of rectangles.
1 Focus
5-Minute Check
Transparency 8-4 Use as a
quiz or review of Lesson 8-3.
• Determine whether parallelograms are rectangles.
Vocabulary
• rectangle
Mathematical Background notes
are available for this lesson on
p. 402D.
are rectangles used in
tennis?
Ask students:
• What kind of lines frequently
are used to make up tennis
courts? parallel and perpendicular
lines
• What other sports playing
fields include parallel and
perpendicular lines? Sample
answers: football, soccer, basketball
Study Tip
Rectangles and
Parallelograms
A rectangle is a
parallelogram, but a
parallelogram is not
necessarily a rectangle.
are rectangles used in tennis?
Many sports are played on fields marked by
parallel lines. A tennis court has parallel lines at
half-court for each player. Parallel lines divide
the court for singles and doubles play. The
service box is marked by perpendicular lines.
PROPERTIES OF RECTANGLES A rectangle is a quadrilateral with four
right angles. Since both pairs of opposite angles are congruent, it follows that it
is a special type of parallelogram. Thus, a rectangle has all the properties of a
parallelogram. Because the right angles make a rectangle a rigid figure, the
diagonals are also congruent.
Theorem 8.13
If a parallelogram is a rectangle, then the
diagonals are congruent.
A
B
A
C
B
D
Abbreviation: If is rectangle, diag. are .
D
C
You will prove Theorem 8.13 in Exercise 40.
If a quadrilateral is a rectangle, then the following properties are true.
Rectangle
Words A rectangle is a quadrilateral with four right angles.
Properties
Examples
1. Opposite sides are congruent
and parallel.
424
A
B
D
C
B
C
A
D
A
B
D
C
B
C
A
D
2. Opposite angles are
congruent.
A C
B D
3. Consecutive angles
are supplementary.
mA mB 180
mB mC 180
mC mD 180
mD mA 180
4. Diagonals are congruent
and bisect each other.
A
C
and B
D
bisect each other.
A
C
B
D
5. All four angles are
right angles.
mDAB mBCD mABC mADC 90
Chapter 8 Quadrilaterals
Simon Bruty/Getty Images
Resource Manager
Workbook and Reproducible Masters
Chapter 8 Resource Masters
• Study Guide and Intervention, pp. 435–436
• Skills Practice, p. 437
• Practice, p. 438
• Reading to Learn Mathematics, p. 439
• Enrichment, p. 440
• Assessment, pp. 473, 475
Graphing Calculator and
Computer Masters, pp. 31, 32
Teaching Geometry With Manipulatives
Masters, pp. 2, 8, 133
Transparencies
5-Minute Check Transparency 8-4
Real-World Transparency 8
Answer Key Transparencies
Technology
Interactive Chalkboard
A
B
D
C
Example 1 Diagonals of a Rectangle
ALGEBRA Quadrilateral MNOP is a rectangle.
If MO 6x 14 and PN 9x 5, find x.
The diagonals of a rectangle are congruent,
P
N
.
so MO
Diagonals of a rectangle are .
MO PN
Definition of congruent segments
2 Teach
O
PROPERTIES OF
RECTANGLES
M
MO
P
N
6x 14 9x 5
P
N
In-Class Examples
Teaching Tip
In Example 1,
remind students that all other
properties of parallelograms
apply to rectangles as well. Since
the diagonals of a parallelogram
bisect each other, students could
1
1
also show that MO PN.
Substitution
14 3x 5
Power
Point®
Subtract 6x from each side.
9 3x
Subtract 5 from each side.
3x
Divide each side by 3.
2
Rectangles can be constructed using perpendicular lines.
2
1 Quadrilateral RSTU is a
rectangle. If RT 6x 4 and
SU 7x 4, find x.
Rectangle
Study Tip
Look Back
To review constructing
perpendicular lines
through a point, see
Lesson 3-6.
1 Use a straightedge to
draw 1
line ᐉ. Label a
Example
point P on ᐉ. Place
the point at P and
locate point Q on ᐉ.
Now construct lines
perpendicular to ᐉ
through P and
through Q. Label
them m and n .
m
n
2 Place the compass
3 Locate the compass
point at P and mark
off a segment on m .
Using the same
compass setting,
place the compass at
Q and mark a segment
on n. Label these
points R and S.
Draw R
S
.
R m
setting that represents
PR and compare to
the setting for QS.
The measures should
be the same.
S
T
R
U
8
2 Quadrilateral LMNP is a
rectangle.
nS
R m
M
nS
N
(6y 2)
P
Q
ᐉ
Q
P
ᐉ
P
ᐉ
Q
(5x 8)
(3x 2)
L
a. Find x. 10
Example 2 Angles of a Rectangle
ALGEBRA Quadrilateral ABCD is a rectangle.
A
a. Find x.
(9x 20)˚
DAB is a right angle, so mDAB 90.
(4x 5)˚
B
(4y 4)˚
mDAC mBAC mDAB
4x 5 9x 20 90
13x 25 90
13x 65
x5
www.geometryonline.com/extra_examples
P
D
b. Find y. 5
(y 2 1)˚
C
Angle Addition Theorem
Substitution
Simplify.
Subtract 25 from each side.
Divide each side by 13.
Lesson 8-4 Rectangles 425
Lesson 8-4 Rectangles 425
b. Find y.
Since a rectangle is a parallelogram, opposite sides are parallel. So, alternate
interior angles are congruent.
PROVE THAT
PARALLELOGRAMS ARE
RECTANGLES
ADB CBD
mADB mCBD
y2 1 4y 4
2
y 4y 5 0
(y 5)(y 1) 0
Teaching Tip
Watch for students
who think that any quadrilateral with
congruent diagonals is a rectangle.
Isosceles trapezoids have congruent
diagonals. Remind them that if the
diagonals of a parallelogram are
congruent, then the parallelogram is
a rectangle.
In-Class Examples
y50
y5
If the diagonals of a parallelogram are congruent,
then the parallelogram is a rectangle.
Abbreviation: If diagonals of are , is a rectangle.
x
O
C
Diagonals of a Parallelogram
First draw a diagram and label the vertices. We know
Z
Y
W
Z
, and W
Y
X
Z
.
that WX
Y
, X
Z
Y
W
X
X
Z
Y
W
Z
, WXYZ is a parallelogram.
Because W
Y
and X
and W
Y
are diagonals and they are congruent. A
XZ
parallelogram with congruent diagonals is a rectangle.
So, the corners are 90° angles.
Windows
It is important to square
the window frame
because over time
the opening may have
become “out-of-square.”
If the window is not
properly situated in
the framed opening, air
and moisture can leak
through cracks.
Example 4 Rectangle on a Coordinate Plane
Source:
www.supersealwindows.com/
guide/measurement
D(–1, –2)
D
WINDOWS Trent is building a tree house for his younger brother. He has
measured the window opening to be sure that the opposite sides are congruent.
He measures the diagonals to make sure that they are congruent. This is called
squaring the frame. How does he know that the corners are 90° angles?
4 Quadrilateral ABCD has
C(5, 0)
B
You will prove Theorem 8.14 in Exercise 41.
C
A
and B
D
are congruent
diagonals. A parallelogram with
congruent diagonals is a rectangle.
A(–2, 1)
A
A
C
B
D
D
B(4, 3)
Factor.
Theorem 8.14
Example 3
y
Subtract 4y and 4 from each side.
y10
y 1 Disregard y 1 because it yields angle measures of 0.
C
vertices A(2, 1), B(4, 3),
C(5, 0), and D(1, 2).
Determine whether ABCD is
a rectangle using the Slope
formula.
Substitution
Theorem 8.13 is also true.
his horse. He measures the
diagonals of the door opening
to make sure they bisect each
other and they are congruent.
How does he know that the
measure of each corner is 90?
A
Definition of angles
PROVE THAT PARALLELOGRAMS ARE RECTANGLES The converse of
Power
Point®
3 Kyle is building a barn for
B
Alternate Interior Angles Theorem
COORDINATE GEOMETRY Quadrilateral FGHJ has
vertices F(4, 1), G(2, 5), H(4, 2), and J(2, 2).
Determine whether FGHJ is a rectangle.
Method 1:
y2 y1
,
Use the Slope Formula, m x2 x1
y
O
F
1
426
Chapter 8 Quadrilaterals
2 (1)
2 (4)
1
2
slope of FJ or 426
x
H
to see if consecutive sides are perpendicular.
slope of A
B
, slope of AD
3
3, slope of BC
3, slope of
1
C
D
. The product of
3
consecutive slopes is 1 so
AB
⊥
BC
, BC
⊥
CD
, CD
⊥
AD
, and
AD
⊥
AB
. The perpendicular
segments create 4 right angles.
Therefore ABCD is a rectangle.
J
G
Chapter 8 Quadrilaterals
Emma Lee/Life File/PhotoDisc
Differentiated Instruction
Kinesthetic Have your students use string, masking tape, and a tiled
floor to mark off congruent diagonals that intersect at their midpoint.
Use the string to show that a rectangle is the polygon with those
diagonals.
2 (5)
1
4 (2)
2
5 (1)
slope of FG
or 2
2 (4)
2 (2)
or 2
slope of JH
24
slope of GH
or 3 Practice/Apply
GH
Because FJ and F
G
JH
, quadrilateral FGHJ is a parallelogram.
The product of the slopes of consecutive sides is 1. This means that F
J FG
,
J JH
, JH
GH
, and F
G
GH
. The perpendicular segments create four right
F
angles. Therefore, by definition FGHJ is a rectangle.
Method 2: Use the Distance Formula, d (x2 x1)2 (y2 y1)2, to determine
whether opposite sides are congruent.
First, we must show that quadrilateral FGHJ is a parallelogram.
FJ (4
2)2 (1 2)2
GH (2 4)2 [5 (2)]2
36 9
36 9
45
45
FG [4 (2)]2
[
1 (
5)]2
Have students—
• add the definitions/examples of
the vocabulary terms to their
Vocabulary Builder worksheets for
Chapter 8.
• include the properties of a rectangle.
• include any other item(s) that they
find helpful in mastering the skills
in this lesson.
JH (2 4
)2 [2
(2
)]2
4 16
4 16
20
20
Since each pair of opposite sides of the quadrilateral have the same measure, they
are congruent. Quadrilateral FGHJ is a parallelogram.
4)2 [1 (2)]2
FH (4
Study Notebook
GJ (2
2)2 (5 2)2
64 1
16 49
65
65
The length of each diagonal is 65
. Since the diagonals are congruent, FGHJ is a
rectangle by Theorem 8.14.
FIND THE ERROR
Exercise 3 gives
students the
opportunity for critical thinking.
This new definition is valid.
Students should recognize that
they can prove that one right
angle in a parallelogram is
sufficient to prove it a rectangle.
About the Exercises…
Concept Check
1. How can you determine whether a parallelogram is a rectangle?
1 – 2. See margin.
2. OPEN ENDED Draw two congruent right triangles with a common hypotenuse.
Do the legs form a rectangle?
3. FIND THE ERROR McKenna and Consuelo are defining a rectangle for an
assignment.
McKenna
Consuelo
A rectangle is a
parallelogram with one
right angle.
A rectangle has a pair of
parallel opposite sides
and a right angle.
Who is correct? Explain. McKenna; Consuelo’s definition is correct if one pair of
opposite sides is parallel and congruent.
Lesson 8-4 Rectangles 427
Odd/Even Assignments
Exercises 10–46 are structured
so that students practice the
same concepts whether they
are assigned odd or even
problems.
Alert! Exercise 37 requires the
Internet or other research
materials.
Assignment Guide
Answers
1. If consecutive sides are
perpendicular or diagonals
are congruent, then the
parallelogram is a
rectangle.
Organization by Objective
• Properties of Rectangles:
10–24, 36–37
• Prove That Parallelograms
Are Rectangles: 25–35, 38–46
2. Sample answer: sometimes
rectangle
not rectangle
Basic: 11–41 odd, 44, 45, 47,
48–63
Average: 11–43 odd, 44, 45, 47,
48–63
Advanced: 10–48 even, 49–60
(optional: 61–63)
Lesson 8-4 Rectangles 427
NAME ______________________________________________ DATE
Guided Practice
____________ PERIOD _____
Study
Guide
andIntervention
Intervention,
8-4
Study
Guide and
p. 435
(shown) and p. 436
Rectangles
GUIDED PRACTICE KEY
Properties of Rectangles A rectangle is a quadrilateral with four
right angles. Here are the properties of rectangles.
T
A rectangle has all the properties of a parallelogram.
•
•
•
•
•
S
Q
U
R
Opposite sides are parallel.
Opposite angles are congruent.
Opposite sides are congruent.
Consecutive angles are supplementary.
The diagonals bisect each other.
Also:
• All four angles are right angles.
• The diagonals are congruent.
UTS, TSR, SRU, and RUT are right angles.
TR
US
Example 1
Exercises
Examples
4–5
6–7
8
9
1
2
4
3
4. ALGEBRA ABCD is a rectangle.
If AC 30 x and BD 4x 60,
find x. 18
D
C
In rectangle RSTU
above, mSTR 8x 3 and mUTR 16x 9. Find mSTR.
UTS is a right angle, so
mSTR mUTR 90.
6x 3 7x 2
3x2
5x
8x 3 16x 9
24x 6
24x
x
A
B
ALGEBRA Quadrilateral QRST is a rectangle.
Find each measure or value.
6. x 5 or 2
7. mRPS 52 or 10
90
90
96
4
mSTR 8x 3 8(4) 3 or 35
Exercises
ABCD is a rectangle.
B
C
E
1. If AE 36 and CE 2x 4, find x. 20
A
2. If BE 6y 2 and CE 4y 6, find y. 2
Lesson 8-4
4. If mBEA 62, find mBAC. 59
5. If mAED 12x and mBEC 10x 20, find mAED. 120
6. If BD 8y 4 and AC 7y 3, find BD. 52
R
(x 2 1)˚ R
Q
P
(3x 11)˚
9. In rectangle MNOP, m1 40. Find the measure of each
numbered angle.
M
6
4
5
1
P
2
3
O
____________
Gl PERIOD
G _____
Skills
Practice,
p. 437 and
8-4
Practice
(Average)
Practice,
Rectanglesp. 438 (shown)
R
Application
N
K
m2 40; m3 50; m4 50; m5 80; m6 100
S
Z
U
S
No; the lengths of the diagonals are not equal: EG 72
and HF 68
.
8. If AB 6y and BC 8y, find BD in terms of y. 10y
1. If UZ x 21 and ZS 3x 15, find US. 78
M
8. COORDINATE GEOMETRY Quadrilateral EFGH has vertices E(4, 3),
F(3, 1), G(2, 3), and H(5, 1). Determine whether EFGH is a rectangle.
7. If mDBC 10x and mACB 4x2 6, find m ACB. 30
ALGEBRA RSTU is a rectangle.
Q
T
D
3. If BC 24 and AD 5y 1, find y. 5
NAME
______________________________________________
DATE
/M
G
Hill
435
N
P
Example 2
In rectangle RSTU
above, US 6x 3 and RT 7x 2.
Find x.
The diagonals of a rectangle bisect each
other, so US RT.
Gl
5. ALGEBRA MNQR is a rectangle.
If NR 2x 10 and NP 2x 30,
find MP. 40
9. FRAMING Mrs. Walker has a rectangular picture that is 12 inches by 48 inches.
Because this is not a standard size, a special frame must be built. What can the
framer do to guarantee that the frame is a rectangle? Justify your reasoning.
Make sure that the angles measure 90 or that the diagonals are congruent.
★ indicates increased difficulty
Practice and Apply
T
2. If RZ 3x 8 and ZS 6x 28, find UZ. 44
3. If RT 5x 8 and RZ 4x 1, find ZT. 9
4. If mSUT 3x 6 and mRUS 5x 4, find mSUT. 39
5. If mSRT x2 9 and mUTR 2x 44, find x. 5 or 7
6. If mRSU x2 1 and mTUS 3x 9, find mRSU. 24 or 3
GHJK is a rectangle. Find each measure if m1 37.
7. m2 53
G
1
2
8. m3 37
9. m4 37
10. m5 53
11. m6 106
12. m7 74
5
6
3
K
7
4
H
J
COORDINATE GEOMETRY Determine whether BGHL is a rectangle given each set
of vertices. Justify your answer.
For
Exercises
See
Examples
10–15,
36–37
16–24
25–26,
35, 38–46
27–34
1
2
3
4
ALGEBRA Quadrilateral JKMN is a rectangle.
J
10. If NQ = 5x 3 and QM 4x 6, find NK. 84
Q
11. If NQ 2x 3 and QK 5x 9, find JQ. 11
2
12. If NM 8x 14 and JK x 1, find JK. 10 or 26
1
13. If mNJM 2x 3 and mKJM x 5, find x. 29 N
3
14. If mNKM x2 4 and mKNM x 30, find mJKN. 22 or 37
15. If mJKN 2x2 2 and mNKM 14x, find x. 4
K
M
Extra Practice
See page 770.
WXYZ is a rectangle. Find each measure if m1 30.
17. m2 60
18. m3 60
16. m1 30
19. m4 30
20. m5 30
21. m6 60
22. m7 60
23. m8 30
24. m9 60
13. B(4, 3), G(2, 4), H(1, 2), L(1, 3)
Yes; sample answer: Opposite sides are parallel and consecutive sides
are perpendicular.
14. B(4, 5), G(6, 0), H(3, 6), L(7, 1)
Yes; sample answer: Opposite sides are congruent and diagonals are
congruent.
15. B(0, 5), G(4, 7), H(5, 4), L(1, 2)
No; sample answer: Diagonals are not congruent.
W
7
X
8
9
6
5
Z
11
12
1
2
4
3
10
Y
16. LANDSCAPING Huntington Park officials approved a rectangular plot of land for a
Japanese Zen garden. Is it sufficient to know that opposite sides of the garden plot are
congruent and parallel to determine that the garden plot is rectangular? Explain.
25. PATIOS A contractor has been hired to pour a rectangular concrete patio. How
can he be sure that the frame in which to pour the concrete is rectangular?
No; if you only know that opposite sides are congruent and parallel, the
most you can conclude is that the plot is a parallelogram.
NAME
______________________________________________
DATE
/M
G
Hill
438
Gl
____________
Gl PERIOD
G _____
Reading
8-4
Readingto
to Learn
Learn Mathematics
Mathematics,
p. 439
Rectangles
Pre-Activity
Measure the opposite sides and the diagonals to make sure they are congruent.
ELL
26. TELEVISION Television screens are
measured on the diagonal. What is the
measure of the diagonal of this screen?
How are rectangles used in tennis?
Read the introduction to Lesson 8-4 at the top of page 424 in your textbook.
Are the singles court and doubles court similar rectangles? Explain your
answer. No; sample answer: All of their angles are congruent,
but their sides are not proportional. The doubles court is wider
in relation to its length.
21 in.
about 42 in.
Reading the Lesson
1. Determine whether each sentence is always, sometimes, or never true.
a. If a quadrilateral has four congruent angles, it is a rectangle. always
36 in.
b. If consecutive angles of a quadrilateral are supplementary, then the quadrilateral
is a rectangle. sometimes
c. The diagonals of a rectangle bisect each other. always
d. If the diagonals of a quadrilateral bisect each other, the quadrilateral is a
rectangle. sometimes
428 Chapter 8 Quadrilaterals
e. Consecutive angles of a rectangle are complementary. never
f. Consecutive angles of a rectangle are congruent. always
g. If the diagonals of a quadrilateral are congruent, the quadrilateral is a
rectangle. sometimes
h. A diagonal of a rectangle bisects two of its angles. sometimes
NAME ______________________________________________ DATE
i. A diagonal of a rectangle divides the rectangle into two congruent right
triangles. always
8-4
Enrichment
Enrichment,
____________ PERIOD _____
p. 440
j. If the diagonals of a quadrilateral bisect each other and are congruent, the
quadrilateral is a rectangle. always
Counting Squares and Rectangles
k. If a parallelogram has one right angle, it is a rectangle. always
l. If a parallelogram has four congruent sides, it is a rectangle. sometimes
2. ABCD is a rectangle with AD AB.
Name each of the following in this figure.
E
A
E
, CE
, DE
a. all segments that are congruent to B
b. all angles congruent to 1 2, 5, 6
B
A
2
3
1
8
E
4
5
7
6
C
D
c. all angles congruent to 7 3, 4, 8
d. two pairs of congruent triangles AED BEC, AEB DEC,
BCD DAB, ABC CDA
Helping You Remember
Each puzzle below contains many squares and/or rectangles.
Count them carefully. You may want to label each region so you
can list all possibilities.
Example
How many rectangles are in the figure
at the right?
Label each small region with a letter. Then list each rectangle
by writing the letters of regions it contains.
A, B, C, D, AB, CD, AC, BD, ABCD
There are 9 rectangles.
3. It is easier to remember a large number of geometric relationships and theorems if you
are able to combine some of them. How can you combine the two theorems about
diagonals that you studied in this lesson? Sample answer: A parallelogram is a
rectangle if and only if its diagonals are congruent.
How many squares are in each figure?
428
Chapter 8 Quadrilaterals
A
B
C
D
COORDINATE GEOMETRY Determine whether DFGH is a rectangle given each
set of vertices. Justify your answer.
27. D(9, 1), F(9, 5), G(6, 5), H(6, 1) No; D
H
and FG
are not parallel.
28. D(6, 2), F(8, 1), G(10, 6), H(12, 3) No; this is not a quadrilateral.
29. D(4, 3), F(5, 8), G(6, 9), H(7, 2) Yes; opp. sides are , diag. are .
COORDINATE GEOMETRY The vertices of WXYZ are W(2, 4), X(2, 0),
Y(1, 7), and Z(9, 3).
30. Find WY and XZ. WY 130
; XZ 130
1
3
7 3
31. Find the coordinates of the midpoints of W
Y
and X
Z
. , , , 2
2
2 2
32. Is WXYZ a rectangle? Explain. No; the midpoints of the diagonals are not the
same, so the diagonals do not bisect each other.
COORDINATE GEOMETRY The vertices of parallelogram ABCD are A(4, 4),
B(2, 1), C(0, 3), and D(6, 0).
33. Determine whether ABCD is a rectangle. Yes; consec. sides are .
34. If ABCD is a rectangle and E, F, G, and H are midpoints of its sides, what can
you conclude about EFGH? It is a parallelogram with all sides congruent.
F
G
35. MINIATURE GOLF The windmill section of a
miniature golf course will be a rectangle 10 feet
B
long and 6 feet wide. Suppose the contractor placed
E A
H
stakes and strings to mark the boundaries with the
6 ft
corners at A, B, C and D. The contractor measured
D
C
D
and A
C
and found that A
C
BD
. Describe
B
10 ft
where to move the stakes L and K to make ABCD a
M
J
rectangle. Explain. Move L and K until the length of
L
K
the diagonals is the same.
Golden
Rectangles
The Parthenon in ancient
Greece is an example
of how the golden
rectangle was applied
to architecture. The ratio
of the length to the
height is the golden ratio.
Source: www.enc.org
GOLDEN RECTANGLES For Exercises 36 and 37, use the following information.
Many artists have used golden rectangles in their work. In a golden rectangle, the
ratio of the length to the width is about 1.618. This ratio is known as the golden ratio.
36. A rectangle has dimensions of 19.42 feet and 12.01 feet. Determine if the
rectangle is a golden rectangle. Then find the length of the diagonal.
37. RESEARCH Use the Internet or other sources to find examples of golden
rectangles. See students’ work.
38. What are the minimal requirements to justify that a parallelogram is a rectangle?
diagonals are congruent or one right angle
39. Draw a counterexample to the statement If the diagonals are congruent, the
quadrilateral is a rectangle. See margin.
PROOF
Write a two-column proof. 40– 41. See margin.
40. Theorem 8.13
★ 42. Given: PQST is a rectangle.
R
V
T
Q
Prove:
41. Theorem 8.14
★ 43. Given: DEAC and FEAB are rectangles.
GKH JHK
G
J and H
K
intersect at L.
P
R
V
S
Prove:
36. Yes, the ratio
of sides is 1.617;
22.83 ft.
42–43. See p. 459B.
Q
R
GHJK is a parallelogram.
S
N
MA
BC
D
G
K
P
V
J
T
E
F
H
L
44. CRITICAL THINKING Using four of the twelve points
as corners, how many rectangles can be drawn? 20
www.geometryonline.com/self_check_quiz
Lesson 8-4 Rectangles 429
Izzet Keribar/Lonely Planet Images
Answers
39. Sample answer: A
C
but
BD
ABCD is not a rectangle.
A
D
40. Given: WXYZ is a rectangle with
diagonals W
Y
and XZ.
Prove: WY
XZ
X
Y
W
Z
Proof:
1. WXYZ is a rectangle with
diagonals W
Y
and X
Z. (Given)
2. W
X
ZY
(Opp. sides of are .)
3. WZ WZ (Reflexive Property)
4. XWZ and YZW are right
angles. (Def. of rectangle)
5. XWZ YZW (All right are .)
6. XWZ YZW (SAS)
7. WY
XZ (CPCTC)
41. Given: WX
YZ, XY
WZ, and
W
Y
XZ
Prove: WXYZ is a rectangle.
W
X
Z
Y
Proof:
1. WX
XY
YZ, WZ, and
WY
XZ (Given)
2. WX
(Reflexive Prop.)
WX
3. WZX XYW (SSS)
4. ZWX YXW (CPCTC)
5. mZWX mYXW (Def.
of )
6. WXYZ is a parallelogram. (If
both pairs of opp. sides are
, then quad. is .)
7. ZWX and YXW are
supplementary. (Cons. of
are suppl.)
8. mZWX mYXW 180
(Def of suppl.)
9. ZWX and YXW are right
angles. (If 2 are and
suppl., each is a rt. .)
10. WZY and XYZ are right
angles. (If has 1 rt. , it
has 4 rt..)
11. WXYZ is a rectangle. (Def. of
rectangle)
B
C
Lesson 8-4 Rectangles 429
4 Assess
Open-Ended Assessment
Writing Have students explain
how to prove that a quadrilateral
with congruent diagonals is a
rectangle.
45. No; there are
no parallel lines in
spherical geometry.
47. No; the sides are
not parallel.
C
A
T
R
Answer the question that was posed at the beginning
of the lesson. See margin.
How are rectangles used in tennis?
48. WRITING IN MATH
Include the following in your answer:
• the number of rectangles on one side of a tennis court, and
• a method to ensure the lines on the court are parallel
Getting Ready for
Lesson 8-5
Prerequisite Skill Students will
learn about the properties of
rhombi and squares in Lesson 8-5.
They will use the Distance
Formula to find information
about rhombi and squares. Use
Exercises 61–63 to determine
your students’ familiarity with
the Distance Formula.
SPHERICAL GEOMETRY The figure shows a Saccheri
quadrilateral on a sphere. Note that it has four sides with
T
T
R, A
R
T
R, and C
T
A
R.
C
45. Is C
T parallel to A
R? Explain.
46. How does AC compare to TR? AC TR
47. Can a rectangle exist in spherical geometry? Explain.
Standardized
Test Practice
CE
B
. If DA 6, what is DB? A
49. In the figure, A
A 6
B 7
C 8
D 9
A
B
6
x˚
E
Note : Figure not
drawn to scale
x˚
D
C
50. ALGEBRA A rectangular playground is surrounded by an 80-foot long fence.
One side of the playground is 10 feet longer than the other. Which of the
following equations could be used to find s, the shorter side of the playground? D
A 10s s 80
B 4s 10 80
C s(s 10) 80
D 2(s 10) 2s 80
Assessment Options
Quiz (Lessons 8-3 and 8-4) is
available on p. 473 of the Chapter 8
Resource Masters.
Mid-Chapter Test (Lessons 8-1
through 8-4) is available on
p. 475 of the Chapter 8 Resource
Masters.
Maintain Your Skills
Mixed Review
For Exercises 52–57, use ABCD. Find each measure
or value. (Lesson 8-2)
52. mAFD 97
53. mCDF 43
54. mFBC 34
55. mBCF 49
56. y 11
57. x 5
Answers
48. Sample answer: The tennis court
is divided into rectangular
sections. The players use the
rectangles to establish the playing
area. Answers should include the
following.
• Not counting overlap, there are
5 rectangles on each side of a
tennis court.
• Measure each diagonal to make
sure they are the same length
and measure each angle to
make sure they measure 90.
3y 4
B
C
54˚
5x
25
F
49˚
A
34˚
29
D
Find the measure of the altitude drawn to the hypotenuse. (Lesson 7-1)
58. Q 612
59.
60. 336
N
18.3 B
24.7
14
18
T
24
34
M
S
Getting Ready for
the Next Lesson
430 Chapter 8 Quadrilaterals
430 Chapter 8 Quadrilaterals
51. TEXTILE ARTS The Navajo people are well
known for their skill in weaving. The design
at the right, known as the Eye-Dazzler, became
popular with Navajo weavers in the 1880s.
How many parallelograms, not including
rectangles, are in the pattern? (Lesson 8-3) 31
R
11
P
27
17.2
297
O
A
C
PREREQUISITE SKILL Find the distance between each pair of points.
(To review the Distance Formula, see Lesson 1-4.)
61. (1, 2), (3, 1) 5
62. (5, 9), (5, 12)
10.4
109
63. (1, 4), (22, 24) 29
Lesson
Notes
Rhombi and Squares
• Recognize and apply the properties of rhombi.
1 Focus
• Recognize and apply the properties of squares.
can you ride a bicycle with
square wheels?
Vocabulary
• rhombus
• square
5-Minute Check
Transparency 8-5 Use as a
quiz or review of Lesson 8-4.
Professor Stan Wagon at Macalester College
in St. Paul, Minnesota, developed a bicycle
with square wheels. There are two front
wheels so the rider can balance without
turning the handlebars. Riding over a
specially curved road ensures a smooth ride.
Mathematical Background notes
are available for this lesson on
p. 402D.
PROPERTIES OF RHOMBI
A square is a special type of parallelogram
called a rhombus. A rhombus is a quadrilateral with all four sides congruent.
All of the properties of parallelograms can be applied to rhombi. There are three
other characteristics of rhombi described in the following theorems.
Rhombus
Theorem
Example
B
8.15
The diagonals of a rhombus are perpendicular.
AC
B
D
8.16
If the diagonals of a parallelogram are
perpendicular, then the parallelogram is
a rhombus. (Converse of Theorem 8.15)
If BD
A
C
, then
ABCD is a rhombus.
Each diagonal of a rhombus bisects a pair of
opposite angles.
DAC BAC DCA BCA
ABD CBD ADB CDB
8.17
A
C
D
can you ride a bicycle
with square wheels?
Ask students:
• Where is the frame of the bicycle
attached to the square wheels?
where the diagonals of the square
intersect
• How can Mr. Wagon get a
smooth ride with this bicycle?
He rides over a specially curved
road.
• How does the curved road
produce a smooth ride? Accept
all reasonable answers.
You will prove Theorems 8.16 and 8.17 in Exercises 35 and 36, respectively.
Example 1 Proof of Theorem 8.15
Study Tip
Given: PQRS is a rhombus.
Proof
Since a rhombus has four
congruent sides, one
diagonal separates the
rhombus into two
congruent isosceles
triangles. Drawing two
diagonals separates the
rhombus into four
congruent right triangles.
Prove:
P
SQ
PR
Q
T
S
R
Proof:
Q
QR
RS
PS
. A rhombus is a
By the definition of a rhombus, P
S
bisects
parallelogram and the diagonals of a parallelogram bisect each other, so Q
at T. Thus, P
T
RT
. Q
T
QT
because congruence of segments is reflexive.
PR
Thus, PQT RQT by SSS. QTP QTR by CPCTC. QTP and QTR also
form a linear pair. Two congruent angles that form a linear pair are right angles.
SQ
by the definition of perpendicular lines.
QTP is a right angle, so PR
Lesson 8-5 Rhombi and Squares 431
Courtesy Professor Stan Wagon/Photo by Deanna Haunsperger
Resource Manager
Workbook and Reproducible Masters
Chapter 8 Resource Masters
• Study Guide and Intervention, pp. 441–442
• Skills Practice, p. 443
• Practice, p. 444
• Reading to Learn Mathematics, p. 445
• Enrichment, p. 446
Prerequisite Skills Workbook, pp. 41–42
Teaching Geometry With Manipulatives
Masters, pp. 8, 16, 134, 135
Transparencies
5-Minute Check Transparency 8-5
Answer Key Transparencies
Technology
Interactive Chalkboard
Lesson x-x Lesson Title 431
Study Tip
2 Teach
Example 2 Measures of a Rhombus
Reading Math
PROPERTIES OF RHOMBI
In-Class Examples
ALGEBRA Use rhombus QRST and the given
information to find the value of each variable.
The plural form of
rhombus is rhombi,
pronounced ROM-bye.
y2
Students may
not believe that a rhombus has
perpendicular diagonals. Ask
groups of students to cut out 4
congruent right triangles. Make
sure each group’s triangles are
unique to that group. Ask them
to join them so they share the
common right angle vertex.
They should form a rhombus.
Share the results with the class.
31 90
Substitution
mTQR mRST Opposite angles are congruent.
mTQR 56
1
2
PROPERTIES OF SQUARES If a quadrilateral is both a rhombus and a
rectangle, then it is a square. All of the properties of parallelograms and rectangles
can be applied to squares.
Example 3 Squares
COORDINATE GEOMETRY Determine whether
parallelogram ABCD is a rhombus, a rectangle,
or a square. List all that apply. Explain.
D
E
432
Chapter 8 Quadrilaterals
Plan
If the diagonals are perpendicular, then
ABCD is either a rhombus or a square.
The diagonals of a rectangle are congruent.
If the diagonals are congruent and
perpendicular, then ABCD is a square.
x
D (3, –1)
C (–1, –3)
Use the Distance Formula to compare the lengths of the diagonals.
AC (1 1
)2 (3
3)2
36 4
4 36
40
40
Use slope to determine whether the diagonals are perpendicular.
1 (1)
3 3
1
3
slope of DB
or 3 3
1 1
slope of A
C
or 3
DB
Since the slope of AC
is the negative reciprocal of the slope of , the
diagonals are perpendicular. The lengths of DB
and A
C
are the same
so the diagonals are congruent. ABCD is a rhombus, a rectangle, and
a square.
Examine You can verify that ABCD is a square by finding the measure and slope
of each side. All four sides are congruent and consecutive sides are
perpendicular.
432 Chapter 8 Quadrilaterals
b. Find mPNL if mMLP 64.
32
Plot the vertices on a coordinate plane.
[3 (
3)] 2 (1
1)2
DB Use rhombus LMNP and the
given information to find
each value.
a. Find y if m1 y2 54.
12 or 12
A (1, 3)
B (–3, 1)
Explore
Solve
2 MEASURES OF A RHOMBUS
P
y
O
Because opposite angles of a
rhombus are congruent and the
diagonals of a rhombus bisect
the angles, BEC DEC DCE BCE and mBEC mDEC mDCE mBCE.
Because EC
bisects BCD,
1
mBCE mBCD. By
2
substitution, mBCE mAEB
and thus, BCE AEB. BE BE by the Reflexive Property and
it is given that AE CE.
Therefore ABE CBE by SAS.
N
Substitution
The diagonals of a rhombus bisect the angles. So, mTQS is (56) or 28.
C
1
Add 31 to each side.
b. Find mTQS if mRST 56.
B
Q
S
The value of y can be 11 or 11.
1
mAEB mBCD
2
L
T
y 11 Take the square root of each side.
1 Given: BCDE is a rhombus,
M
3
The diagonals of a rhombus are perpendicular.
y2 121
R
2
P
m3 90
Teaching Tip
A
1
a. Find y if m3 y2 31.
Power
Point®
E
CE
.
A
Prove: ABE CBE
Q
PROPERTIES OF SQUARES
Rhombus
A
D.
1 Draw any segment Place the compass
point at A, open to
the width of AD, and
D.
draw an arc above A
2 Label any point on the
3 Place the compass
arc as B. Using the
same setting, place
the compass at B,
and draw an arc to
the right of B.
4 Use a straightedge to
at D, and draw an
arc to intersect the
arc drawn from B.
Label the point of
intersection C.
B
B
draw AB
BC
, ,
and CD
.
parallelogram ABCD is a
rhombus, a rectangle, or a
square for A(2, 1), B(1, 3),
C(3, 2), and D(2, 2). List all
that apply.
C
AC 34
; BD 34
; slope of
3
A
D
D
Conclusion: Since all of the sides are congruent, quadrilateral ABCD is a rhombus.
Example 4 Diagonals of a Square
BASEBALL The infield of a baseball
diamond is a square, as shown at the
right. Is the pitcher’s mound located
in the center of the infield? Explain.
Since a square is a parallelogram, the
diagonals bisect each other. Since a square
is a rhombus, the diagonals are congruent.
Therefore, the distance from first base to
third base is equal to the distance between
home plate and second base.
5
A
C ; slope of B
D . Since
5
3
the slope of A
C
is the negative
reciprocal of the slope of B
D
, the
diagonals are perpendicular. The
lengths of A
C
and B
D
are the
same. ABCD is a rhombus, a
rectangle, and a square.
D
A
D
A
A
Power
Point®
3 Determine whether
B
C
In-Class Examples
4 A square table has four legs
that are 2 feet apart. The
table is placed over an
umbrella stand so that the
hole in the center of the table
lines up with the hole in the
stand. How far away from a
leg is the center of the hole?
about 1.4 ft
2nd
90 ft
3rd
Pitcher
127 ft 3 3 in.
1st
8
60 ft 6 in.
Home
Thus, the distance from home plate to the
Teaching Tip
3
8
center of the infield is 127 feet 3 inches
11
divided by 2 or 63 feet 7 inches. This distance is longer than the distance from
16
home plate to the pitcher’s mound so the pitcher’s mound is not located in the
center of the field. It is about 3 feet closer to home.
This construction
for a rhombus can be adapted
to construct a parallellogram. In
Step 1, have students draw an
arc that is not the same length
D
.
as A
If a quadrilateral is a rhombus or a square, then the following properties are true.
Study Tip
Square and
Rhombus
A square is a rhombus,
but a rhombus is not
necessarily a square.
Properties of Rhombi and Squares
Rhombi
Squares
1. A rhombus has all the properties
of a parallelogram.
1. A square has all the properties of a
parallelogram.
2. All sides are congruent.
2. A square has all the properties of
a rectangle.
3. Diagonals are perpendicular.
4. Diagonals bisect the angles of
the rhombus.
www.geometryonline.com/extra_examples
3. A square has all the properties of
a rhombus.
Lesson 8-5 Rhombi and Squares
433
Differentiated Instruction
Auditory/Musical Ask students to name the similarities and the
differences between rhombi, rectangles, and squares.
Lesson 8-5 Rhombi and Squares 433
3 Practice/Apply
Concept Check
2. OPEN ENDED Draw a quadrilateral that has the characteristics of a rectangle,
a rhombus, and a square.
Study Notebook
Have students—
• add the definitions/examples of
the vocabulary terms to their
Vocabulary Builder worksheets for
Chapter 8.
• include a list of properties of
rhombi and squares.
• include any other item(s) that they
find helpful in mastering the skills
in this lesson.
1. Draw a diagram to demonstrate the relationship among parallelograms,
rectangles, rhombi, and squares. 1–2. See margin.
3. Explain the difference between a square and a rectangle.
A square is a rectangle with all sides congruent.
Guided Practice
GUIDED PRACTICE KEY
Exercises
Examples
4–7
8–9
10
11
2
3
1
4
ALGEBRA In rhombus ABCD, AB 2x 3 and BC 5x.
5. Find AD. 5
4. Find x. 1
6. Find mAEB. 90 7. Find mBCD if mABC 83.2. 96.8
B
A
E
D
C
COORDINATE GEOMETRY Given each set of vertices, determine whether MNPQ
is a rhombus, a rectangle, or a square. List all that apply. Explain your reasoning.
8. M(0, 3), N(3, 0), P(0, 3), Q(3, 0)
9. M(4, 0), N(3, 3), P(2, 2), Q(1, 1) None; the diagonals are not congruent or
8. rectangle, rhombus,
square; consecutive
perpendicular.
sides are perpendicular;
all sides are congruent. 10. PROOF Write a two-column proof. See p. 459B.
G
H
Given: KGH, HJK, GHJ, and JKG are isosceles.
Prove: GHJK is a rhombus.
About the Exercises…
Organization by Objective
• Properties of Rhombi: 12–19,
37–42
• Properties of Squares: 20–36
Odd/Even Assignments
Exercises 12–43 are structured
so that students practice the
same concepts whether they
are assigned odd or even
problems.
Assignment Guide
Basic: 13–33 odd, 39, 41, 43–67
Average: 13–43 odd, 44–67
Advanced: 12–44 even, 45–63
(optional: 64–67)
1. Sample answer:
Square
(rectangle
with 4 sides)
Rhombus
( with 4
sides)
Parallelogram
(opposite sides || )
2. Sample answer:
434
Application
Chapter 8 Quadrilaterals
J
11. REMODELING The Steiner family is remodeling their kitchen. Each side of the
floor measures 10 feet. What other measurements should be made to determine
whether the floor is a square? If the measure of each angle is 90 or if the
diagonals are congruent, then the floor is a square.
★ indicates increased difficulty
Practice and Apply
For
Exercises
See
Examples
12–19
20–23
24–36
37–42
2
3
4
1
Extra Practice
See page 770.
22. Square, rectangle,
rhombus; all sides
are congruent and
perpendicular.
Answers
Rectangle
( with
1 right )
K
434 Chapter 8 Quadrilaterals
In rhombus ABCD, mDAB 2mADC and CB 6.
13. Find mDAB. 120
12. Find mACD. 60
14. Find DA. 6
15. Find mADB. 30
C
D
6
E
A
ALGEBRA Use rhombus XYZW with mWYZ 53, VW 3,
5a 1
XV 2a 2, and ZV .
4
16. Find mYZV. 37
17. Find mXYW. 53
18. Find XZ. 8
19. Find XW. 5
B
Y
X
53˚
V
W
Z
COORDINATE GEOMETRY Given each set of vertices, determine whether EFGH
is a rhombus, a rectangle, or a square. List all that apply. Explain your reasoning.
20. E(1, 10), F(4, 0), G(7, 2), H(12, 12) Rhombus; the diagonals are perpendicular.
21. E(7, 3), F(2, 3), G(1, 7), H(4, 7) Rhombus; the diagonals are perpendicular.
22. E(1, 5), F(6, 5), G(6, 10), H(1, 10)
23. E(2, 1), F(4, 3), G(1, 5), H(3, 1) None; the diagonals are not congruent
or perpendicular.
Unlocking Misconceptions
A common error is to believe that all rectangles are squares and that all
squares are rectangles. It is true that all squares are rectangles, but the
converse is not true. Ask students to verify this by giving several
counterexamples.
CONSTRUCTION
NAME ______________________________________________ DATE
Construct each figure using a compass and ruler.
____________ PERIOD _____
Study
Guide
andIntervention
Intervention,
8-5
Study
Guide and
p. 441
Rhombi(shown)
and Squares and p. 442
24. a square with one side 3 centimeters long 24– 25. See margin.
Properties of Rhombi A rhombus is a quadrilateral with four
congruent sides. Opposite sides are congruent, so a rhombus is also a
parallelogram and has all of the properties of a parallelogram. Rhombi
also have the following properties.
25. a square with a diagonal 5 centimeters long
Use the Venn diagram to determine
whether each statement is always,
sometimes, or never true.
26. A parallelogram is a square. sometimes
Quadrilaterals
Rectangles
Rhombi
H
B
The diagonals are perpendicular.
MH
⊥
RO
Each diagonal bisects a pair of opposite angles.
MH
bisects RMO and RHO.
O
R
bisects MRH and MOH.
If the diagonals of a parallelogram are
perpendicular, then the figure is a rhombus.
O
⊥
MH
,
If RHOM is a parallelogram and R
then RHOM is a rhombus.
Example
In rhombus ABCD, mBAC 32. Find the
measure of each numbered angle.
ABCD is a rhombus, so the diagonals are perpendicular and ABE
is a right triangle. Thus m4 90 and m1 90 32 or 58. The
diagonals in a rhombus bisect the vertex angles, so m1 m2.
Thus, m2 58.
Parallelograms
27. A square is a rhombus. always
R
M
O
B
12
32 4
A
E
3
C
D
A rhombus is a parallelogram, so the opposite sides are parallel. BAC and 3 are
alternate interior angles for parallel lines, so m3 32.
Exercises
28. A rectangle is a parallelogram. always
ABCD is a rhombus.
Squares
29. A rhombus is a rectangle. sometimes
B
C
E
1. If mABD 60, find mBDC. 60
2. If AE 8, find AC. 16
3. If AB 26 and BD 20, find AE. 24
4. Find mCEB. 90
5. If mCBD 58, find mACB. 32
6. If AE 3x 1 and AC 16, find x. 3
30. A rhombus is a square. sometimes
7. If mCDB 6y and mACB 2y 10, find y. 10
31. A square is a rectangle. always
9. a. What is the midpoint of FH
? (5, 5)
A
D
8. If AD 2x 4 and CD 4x 4, find x. 4
y
J
H
b. What is the midpoint of GJ
? (5, 5)
c. What kind of figure is FGHJ? Explain.
1
d. What is the slope of F
H ? 2
e. What is the slope of G
J
? 2
f. Based on parts c, d, and e, what kind of figure is FGHJ ? Explain.
FGHJ is a parallelogram with perpendicular diagonals,
so it is a rhombus.
Gl
NAME
______________________________________________
DATE
/M
G
Hill
441
Skills
Practice,
8-5
Practice
(Average)
1. Find PY.
40
The plant stand is
constructed from painted
wood and metal. The
overall dimensions are
1
36 inches tall by
2
3
15 inches wide.
4
3
8. Find PM.
6
is a rhombus, a rectangle, or a square. List all that apply. Explain your reasoning.
9. B(9, 1), E(2, 3), F(12, 2), G(1, 4)
K
Rhombus; all sides are congruent and the diagonals are perpendicular,
but not congruent.
M
L
10. B(1, 3), E(7, 3), F(1, 9), G(5, 3)
Rhombus, rectangle, square; all sides are congruent and the diagonals
are perpendicular and congruent.
Write a paragraph proof for each theorem. 35–36. See p. 459C.
★ 35. Theorem 8.16
Q
COORDINATE GEOMETRY Given each set of vertices, determine whether BEFG
D
PROOF
P
A
M
45
90
C
N
6. Find mAPQ.
7. Find mMNP.
H
J
A
is a rhombus; EFGH and JKLM are
congruent squares.
Source: www.metmuseum.org
90
5. Find AQ.
G
Z
4. Find mYKZ.
Use rhombus MNPQ with PQ 32
, PA 4x 1, and
AM 9x 6.
F
E
K
P
42
29
B
Y
R
2. Find RZ.
3. Find RY.
Design
____________
Gl PERIOD
G _____
p. 443 and
Practice,
p.Squares
444 (shown)
Rhombi and
Use rhombus PRYZ with RK 4y 1, ZK 7y 14,
PK 3x 1, and YK 2x 6.
33. PERIMETER The diagonals of a rhombus are 12 centimeters and
16 centimeters long. Find the perimeter of the rhombus. 40 cm
34. ART This piece of art is Dorthea
Rockburne’s Egyptian Painting:
Scribe. The diagram shows three of
the shapes shown in the piece. Use
a ruler or a protractor to determine
which type of quadrilateral is
represented by each figure. ABCD
x
O
Lesson 8-5
32. DESIGN Otto Prutscher designed the plant stand at the left in 1903.
The base is a square, and the base of each of the five boxes is also a
square. Suppose each smaller box is one half as wide as the base.
Use the information at the left to find the dimensions of the base of
one of the smaller boxes. 77in. by 7 7 in.
8
8
G
F
FGHJ is a parallelogram because
the diagonals bisect each other.
11. B(4, 5), E(1, 5), F(7, 1), G(2, 1)
None; two of the opposite sides are not congruent.
★ 36. Theorem 8.17
12. TESSELATIONS The figure is an example of a tessellation. Use a ruler
or protractor to measure the shapes and then name the quadrilaterals
used to form the figure.
SQUASH For Exercises 37 and 38,
use the diagram of the court for squash,
a game similar to racquetball and
tennis.
★ 37. The diagram labels the diagonal as
11,665 millimeters. Is this correct?
Explain. No; it is about 11,662.9 mm.
The figure consists of 6 congruent rhombi.
Gl
NAME
______________________________________________
DATE
/M
G
Hill
444
____________
Gl PERIOD
G _____
Reading
8-5
Readingto
to Learn
Learn Mathematics
Service
Boxes
5640 mm
Mathematics,
p. 445
Rhombi and Squares
Pre-Activity
ELL
How can you ride a bicycle with square wheels?
Read the introduction to Lesson 8-5 at the top of page 431 in your textbook.
If you draw a diagonal on the surface of one of the square wheels shown in
the picture in your textbook, how can you describe the two triangles that are
formed? Sample answer: two congruent isosceles right triangles
6400 mm
11,665 mm
Reading the Lesson
★ 38. The service boxes are squares.
1. Sketch each of the following. Sample answers are given.
Find the length of the diagonal.
1600 mm
9750 mm
about 2263 mm or 2.263 m
a. a quadrilateral with perpendicular
diagonals that is not a rhombus
b. a quadrilateral with congruent
diagonals that is not a rectangle
Lesson 8-5 Rhombi and Squares 435
(l)Metropolitan Museum of Art. Purchase, Lila Acheson Wallace Gift, 1993 (1993.303a-f), (r)courtesy Dorothea Rockburne and Artists Rights Society
NAME ______________________________________________ DATE
Answers
8-5
Enrichment
Enrichment,
25. Sample answer:
a. The diagonals are congruent. rectangle, square
p. 446
b. Opposite sides are congruent. parallelogram, rectangle, rhombus, square
c. The diagonals are perpendicular. rhombus, square
d. Consecutive angles are supplementary. parallelogram, rectangle, rhombus,
Creating Pythagorean Puzzles
e. The quadrilateral is equilateral. rhombus, square
By drawing two squares and cutting them in a certain way, you
can make a puzzle that demonstrates the Pythagorean Theorem.
A sample puzzle is shown. You can create your own puzzle by
following the instructions below.
square
f. The quadrilateral is equiangular. rectangle, square
g. The diagonals are perpendicular and congruent. square
h. A pair of opposite sides is both parallel and congruent. parallelogram, rectangle,
rhombus, square
a
3. What is the common name for a regular quadrilateral? Explain your answer. Square;
3 cm
3 cm
2. List all of the following special quadrilaterals that have each listed property:
parallelogram, rectangle, rhombus, square.
sample answer: All four sides of a square are congruent and all four
angles are congruent.
b
5 cm
Helping You Remember
a
b
b
X
4. A good way to remember something is to explain it to someone else. Suppose that your
classmate Luis is having trouble remembering which of the properties he has learned in
this chapter apply to squares. How can you help him? Sample answer: A square is
a parallelogram that is both a rectangle and a rhombus, so all properties
of parallelograms, rectangles, and rhombi apply to squares.
See students’ work A sample answer is shown
Lesson 8-5 Rhombi and Squares 435
Lesson 8-5
24. Sample answer:
____________ PERIOD _____
c. a quadrilateral whose diagonals are
perpendicular and bisect each other,
but are not congruent
39. FLAGS Study the flags shown below. Use a ruler and protractor to determine if
any of the flags contain parallelograms, rectangles, rhombi, or squares. See margin.
Answers
39. The flag of Denmark contains four
red rectangles. The flag of St.
Vincent and the Grenadines
contains a blue rectangle, a green
rectangle, a yellow rectangle, a
blue and yellow rectangle, a
yellow and green rectangle, and
three green rhombi. The flag of
Trinidad and Tobago contains two
white parallelograms and one
black parallelogram.
40. Given: WZY WXY
WZY and XYZ are
isosceles.
Prove: WXYZ is a rhombus.
W
Flags
The state of Ohio has
the only state flag in
the United States that
is not rectangular.
Source: World Almanac
Denmark
PROOF
St. Vincent and
The Grenadines
Trinidad and Tobago
Write a two-column proof. 40 – 43. See margin.
40. Given:
Prove:
WZY WXY, WZY
and XYZ are isosceles.
WXYZ is a rhombus.
W
41. Given: TPX QPX QRX TRX
Prove:
TPQR is a rhombus.
X
P
X
P
X
Z
Q
Y
T
R
P
Z
Y
42. Given:
Proof:
Statements (Reasons)
1. WZY WXY; WZY and
XYZ are isosceles. (Given)
2. WZ
, ZY
(CPCTC)
WX
XY
3. WZ ZY
, WX
XY
(Def. of isosceles )
4. WZ ZY
WX
XY
(Substitution Property)
5. WXYZ is a rhombus. (Def. of
rhombus)
41. Given: TPX QPX QRX TRX
Prove: TPQR is a rhombus.
P
Prove:
LGK MJK
GHJK is a parallelogram.
GHJK is a rhombus.
QRT is equilateral.
Q
R
M
L
V
G
44. CRITICAL THINKING
The pattern at the right
is a series of rhombi
that continue to form a
hexagon that increases
in size. Copy and
complete the table.
H
Hexagon
3
2
12
3
27
4
48
5
75
108
3x 2
x
T
Number of
rhombi
1
6
X
R
Proof:
Statements (Reasons)
1. TPX QPX QRX TRX (Given)
2. TP
PQ
QR
TR
(CPCTC)
3. TPQR is a rhombus. (Def. of
rhombus)
42. Given: LGK MJK
GHJK is a parallelogram.
Prove: GHJK is a rhombus.
J
K
M
L
G
436
Prove:
J
K
Q
T
43. Given: QRST and QRTV are
rhombi.
H
Chapter 8 Quadrilaterals
Answer the question that was posed at the beginning of
the lesson. See margin.
How can you ride a bicycle with square wheels?
45. WRITING IN MATH
Include the following in your answer:
• difference between squares and rhombi, and
• how nonsquare rhombus-shaped wheels would work with the curved road.
436 Chapter 8 Quadrilaterals
Proof:
Statements (Reasons)
1. LGK MJK; GHJK is a parallelogram. (Given)
2. KG
KJ (CPCTC)
3. KJ GH
, KG
JH
(Opp. sides of are .)
4. KG
JH
GH
JK
(Substitution Property)
5. GHJK is a rhombus. (Def. of rhombus)
S
Standardized
Test Practice
46. Points A, B, C, and D are on a square. The area of the square is 36 square units.
Which of the following statements is true? B
A The perimeter of rectangle ABCD is
greater than 24 units.
C
B
B The perimeter of rectangle ABCD is
less than 24 units.
A
D
C The perimeter of rectangle ABCD is
equal to 24 units.
D The perimeter of rectangle ABCD cannot
be determined from the information given.
1x
47. ALGEBRA For all integers x 2, let <x> . Which of the following has
x2
the greatest value? C
A <0>
B <1>
C <3>
D <4>
Maintain Your Skills
Mixed Review
ALGEBRA Use rectangle LMNP, parallelogram LKMJ, and
the given information to solve each problem. (Lesson 8-4)
48. If LN 10, LJ 2x 1, and PJ 3x 1, find x. 2
49. If mPLK 110, find mLKM. 140
50. If mMJN 35, find mMPN. 17.5
51. If MK 6x, KL 3x 2y, and JN 14 x,
find x and y. x 2, y 3
52. If mLMP mPMN, find mPJL. 90
P
Open-Ended Assessment
Modeling Have students
construct a square by connecting
the vertices of two congruent
straws that intersect at their
midpoints. Ask them if they can
construct a rhombus from the
same two straws. Ask them to
describe the rhombus.
Getting Ready for
Lesson 8-6
L
K
J
N
4 Assess
M
Prerequisite Skill Students will
learn about trapezoids in Lesson
8-6. They will solve equations to
find the measures of angles and
sides of trapezoids. Use Exercises
64–67 to determine your students’
familiarity with solving equations.
COORDINATE GEOMETRY Determine whether the points are the vertices
of a parallelogram. Use the method indicated. (Lesson 8-3)
53. P(0, 2), Q(6, 4), R(4, 0), S(2, 2); Distance Formula yes
54. F(1, 1), G(4, 1), H(3, 4), J(2, 1); Distance Formula no
55. K(3, 7), L(3, 2), M(1, 7), N(3, 1); Slope Formula no
56. A(4, 1), B(2, 5), C(1, 7), D(3, 3); Slope Formula yes
Refer to PQS. (Lesson 6-4)
57. If RT 16, QP 24, and ST 9, find PS. 13.5
58. If PT y 3, PS y 2, RS 12, and QS 16,
solve for y. 4 2
3
59. If RT 15, QP 21, and PT 8, find TS. 20
Q
R
P
Refer to the figure. (Lesson 4-6)
60. If A
AC
G
, name two congruent angles. AGC ACG
61. If A
J
A
H
, name two congruent angles. AJH AHJ
62. If AFD ADF, name two congruent segments. A
AD
F
63. If AKB ABK, name two congruent segments. A
AB
K
Getting Ready for
the Next Lesson
S
T
A
K
G
J H
F
D
B
C
PREREQUISITE SKILL Solve each equation.
(To review solving equations, see pages 737 and 738.)
1
64. (8x 6x 7) 5 8.5
1
65. (7x 3x 1) 12.5 2.4
1
66. (4x 6 2x 13) 15.5 2
1
67. (7x 2 3x 3) 25.5 5
2
2
www.geometryonline.com/self_check_quiz
2
2
Lesson 8-5 Rhombi and Squares
437
Answers
43. Given: QRST and QRTV are rhombi.
Prove: QRT is equilateral.
Q
V
R
T
S
Proof:
Statements (Reasons)
1. QRST and QRTV are rhombi. (Given)
2. QV
VT TR
QR
, QR
TS
RS
Q
T
(Def. of rhombus)
3. TR
QR
Q
T (Transitive Property)
4. QRT is equilateral. (Def. of equilateral triangle)
45. Sample answer: You can ride a
bicycle with square wheels over a
curved road. Answers should
include the following.
• Rhombi and squares both have
all four sides congruent, but the
diagonals of a square are
congruent. A square has four
right angles and rhombi have
each pair of opposite angles
congruent, but not all angles
are necessarily congruent.
• Sample answer: Since the
angles of a rhombus are not all
congruent, riding over the same
road would not be smooth.
Lesson 8-5 Rhombi and Squares 437
Geometry
Activity
A Follow-Up to Lesson 8-5
A Follow-Up of Lesson 8-5
Getting Started
Objective Construct a kite
Materials compass
Discuss why the compass setting
has to be increased (or decreased)
when drawing the second pair of
sides for the kite. (If the compass
setting is the same, the figure will
have four congruent sides and be
a rhombus.)
Kites
A kite is a quadrilateral with exactly two distinct pairs
of adjacent congruent sides. In kite ABCD, diagonal B
D
separates the kite into two congruent triangles. Diagonal
A
C
separates the kite into two noncongruent isosceles
triangles.
B
A
C
D
Activity
Construct a kite QRST.
T
.
1 Draw R
R
T
Teach
You may want students to do
this activity in groups of four.
Ask one student to construct the
kite. Ask another student to
measure each of the angles in the
kite and make a conjecture. Ask
a third student to measure the
distance from the vertices of the
kite to the intersection of the
diagonals of the kite and make a
conjecture. Ask the fourth
student to make conjectures
about the triangles formed by
the diagonals of the kite.
1
2
2 Choose a compass setting greater than R
T
. Place
the compass at point R and draw an arc above R
T
.
Then without changing the compass setting, move the
compass to point T and draw an arc that intersects the
first one. Label the intersection point Q. Increase the
compass setting. Place the compass at R and draw an arc
below R
T
. Then, without changing the compass setting,
draw an arc from point T to intersect the other arc.
Label the intersection point S.
3 Draw QRST.
Q
R
T
S
Q
R
T
S
Model
Assess
As students complete Exercise 6,
list their conjectures on the board
and discuss as a class.
1. Draw Q
S in kite QRST. Use a protractor to measure the angles formed by the
intersection of Q
S and R
T
. The diagonals intersect at a right angle.
2. Measure the interior angles of kite QRST. Are any congruent? QRS QTS
3. Label the intersection of Q
S and R
T
as point N. Find the lengths of Q
N
, N
S, T
N
,
and N
R
. How are they related? See students’ work; N
R
TN
, but QN
NS.
4. How many pairs of congruent triangles can be found in kite QRST?
5. Construct another kite JKLM. Repeat Exercises 1–4. See p. 459C.
4. 3 pairs: QRN QTN, RNS TNS, QRS QTS
Analyze
6. Use your observations and measurements of kites QRST and JKLM to make
conjectures about the angles, sides, and diagonals of kites. See p. 459C.
438 Chapter 8 Quadrilaterals
Resource Manager
Study Notebook
Ask students to summarize what
they have learned about the
properties of a kite.
438 Chapter 8 Quadrilaterals
Teaching Geometry with
Manipulatives
Glencoe Mathematics Classroom
Manipulative Kit
• p. 136 (student recording sheet)
• compass
Lesson
Notes
Trapezoids
• Recognize and apply the properties of trapezoids.
1 Focus
• Solve problems involving the medians of trapezoids.
are trapezoids used in architecture?
Vocabulary
• trapezoid
• isosceles trapezoid
• median
5-Minute Check
Transparency 8-6 Use as a
quiz or review of Lesson 8-5.
The Washington Monument in Washington, D.C., is
an obelisk made of white marble. The width of the
base is longer than the width at the top. Each face of
the monument is an example of a trapezoid.
PROPERTIES OF TRAPEZOIDS A trapezoid is a quadrilateral with exactly
one pair of parallel sides. The parallel sides are called bases. The base angles are
formed by a base and one of the legs. The nonparallel sides are called legs.
A and B are base angles.
A
base
B
leg
leg
D
C
C and D are base angles.
base
If the legs are congruent, then the trapezoid is an isosceles trapezoid. Theorems
8.18 and 8.19 describe two characteristics of isosceles trapezoids.
Theorems
Study Tip
Isosceles
Trapezoid
If you extend the legs of
an isosceles trapezoid
until they meet, you will
have an isosceles triangle.
Recall that the base angles
of an isosceles triangle
are congruent.
8.18
Both pairs of base angles
of an isosceles trapezoid
are congruent.
Example:
DAB CBA
ADC BCD
8.19
The diagonals of an isosceles
trapezoid are congruent.
AC
BD
A
B
D
Mathematical Background notes
are available for this lesson on
p. 402D.
are trapezoids used in
architecture?
Ask students:
• What is the shape of the base
of the obelisk? square
• How many sides does the base
of the obelisk have? 4
• How is a trapezoid different
from other shapes you have
studied? Accept all reasonable
answers.
C
You will prove Theorem 8.18 in Exercise 36.
Example 1 Proof of Theorem 8.19
Write a flow proof of Theorem 8.19.
Given: MNOP is an isosceles trapezoid.
Prove:
M
O
NP
M
Proof:
MP NO
MPO NOP
Base s of isos.
O
P
Def. of isos. trapezoid
MNOP is an
isosceles trapezoid.
Given
N
MPO NOP
MO NP
SAS
CPCTC
trap. are .
PO PO
Reflexive Property
Lesson 8-6 Trapezoids 439
Bill Bachmann/PhotoEdit
Resource Manager
Workbook and Reproducible Masters
Chapter 8 Resource Masters
• Study Guide and Intervention, pp. 447–448
• Skills Practice, p. 449
• Practice, p. 450
• Reading to Learn Mathematics, p. 451
• Enrichment, p. 452
• Assessment, p. 474
School-to-Career Masters, p. 16
Teaching Geometry With Manipulatives
Masters, pp. 8, 137
Transparencies
5-Minute Check Transparency 8-6
Answer Key Transparencies
Technology
GeomPASS: Tutorial Plus, Lesson 17
Interactive Chalkboard
Lesson x-x Lesson Title 439
Example 2 Identify Isoceles Trapezoids
2 Teach
ART The sculpture pictured is Zim Zum I by
Barnett Newman. The walls are connected at right
angles. In perspective, the rectangular panels
appear to be trapezoids. Use a ruler and protractor
to determine if the images of the front panels are
isosceles trapezoids. Explain.
The panel on the left is an isosceles trapezoid. The
bases are parallel and are different lengths. The legs
are not parallel and they are the same length.
PROPERTIES OF
TRAPEZOIDS
In-Class Examples
Power
Point®
1 Write a flow proof.
Given: KLMN is an isosceles
trapezoid.
Prove: LKM MNL
L
K
M
The panel on the right is not an isosceles trapezoid.
Each side is a different length.
Art
N
See bottom of page for flow proof.
2 The top of this work station
appears to be two adjacent
trapezoids. Use a ruler and
protractor to determine if
they are isosceles trapezoids.
Barnett Newman designed
this piece to be 50% larger.
This piece was built for an
exhibition in Japan but it
could not be built as large
as the artist wanted
because of size limitations
on cargo from New York
to Japan.
Example 3 Identify Trapezoids
Source: www.sfmoma.org
K (6, 8)
J (18, 1)
20 10 O
10 20
10
x
A quadrilateral is a trapezoid if exactly one pair of
opposite sides are parallel. Use the Slope Formula.
M (18, 26)
1 8
slope of JK
1 (26)
slope of M
L
1 (26)
slope of JM
18
slope of K
L
30
18 (18)
27
3
or 36
4
18 (6)
7
24
b. Determine whether JKLM is an isosceles trapezoid. Explain.
First use the Distance Formula to show that the legs are congruent.
a. Verify that ABCD is a
trapezoid.
JM [18 (18)
]2 [
1 (
26)]2
1
1
Slope of A
B ; slope of C
D ;
4
4
slope of A
D
1; slope of B
C
4. Since A
B and C
D have the
same slope, AB
|| C
D. Exactly one
pair of opposite sides is parallel.
Therefore, ABCD is a trapezoid.
KL (6
18)2 (8 1
)2
0 625
576 49
625
or 25
625
or 25
Since the legs are congruent, JKLM is an isosceles trapezoid.
MEDIANS OF TRAPEZOIDS The segment that
median
joins midpoints of the legs of a trapezoid is the median .
The median of a trapezoid can also be called a midsegment.
Recall from Lesson 6-4 that the midsegment of a triangle is
the segment joining the midpoints of two sides. The median
of a trapezoid has the same properties as the midsegment of a triangle. You
can construct the median of a trapezoid using a compass and a straightedge.
440
Chapter 8 Quadrilaterals
(l)Bernard Gotfryd/Woodfin Camp & Associates, (r)San Francisco Museum of Modern Art. Purchased through a gift of Phyllis Wattis/©Barnett Newman Foundation/Artists Rights Society, New York
Proof:
KLMN is an
isosceles
trapezoid.
Given
KM NL
Diag.of an
isos. trap. are .
KL NM
KLM NML
LKM MNL
Def. of isos. trap.
SSS
CPCTC
LM ML
Reflexive Prop.
Chapter 8 Quadrilaterals
L(18, 1)
Exactly one pair of opposite sides are parallel, JK
and M
L
.
So, JKLM is a trapezoid.
vertices A(5, 1), B(3, 1),
C(2, 3), and D(2, 4).
440
10
20
a. Verify that JKLM is a trapezoid.
18 (18)
25
or undefined
0
3 ABCD is a quadrilateral with
b. Determine whether ABCD is
an isosceles trapezoid. Explain.
BC 17
, and AD 18
;
since the legs are not congruent,
ABCD is not an isosceles
trapezoid.
COORDINATE GEOMETRY JKLM is a quadrilateral
with vertices J(18, 1), K(6, 8), L(18, 1), and
M(18, 26).
18 (6)
9
3
or 12
4
yes
y
20
MEDIANS OF TRAPEZOIDS
Study Tip
Reading Math
The word median means
middle. The median of a
trapezoid is the segment
that is parallel to and
equidistant from
each base.
Median of a Trapezoid
In-Class Examples
Model
1 Draw trapezoid
WXYZ with legs XY
and W
Z
.
W
MN
.
3 Draw 2 Construct the
perpendicular
bisectors of X
Y
and W
Z
. Label the
midpoints M and N.
X
W
X
Teaching Tip
X
W
N
N
M
Y
Z
Z
M
Y
Y
Z
Analyze
1. Measure WX
ZY
MN
, , and to the nearest millimeter. See students’ work.
1
2. Make a conjecture based on your observations. MN (WX ZY )
2
You may want to
stress the differences between a
trapezoid and a parallelogram. A
trapezoid has exactly one pair of
opposite sides parallel, while a
parallelogram has exactly two.
Caution students that they should
not assume all trapezoids are
isosceles.
4 DEFG is an isosceles
N
.
trapezoid with median M
E
M
The results of the Geometry Activity suggest Theorem 8.20.
D
1
Example: EF (AB DC)
A
B
E
D
C
2
Example 4 Median of a Trapezoid
1
XY (QR TS)
2
1
15 (22 TS)
2
30 22 TS
8 TS
R
1
Theorem 8.20
2
X
Y
3
Substitution
T
4
F
N
2
G
b. Find m1, m2, m3, and
m4 if m1 3x 5 and
m3 6x 5. m1 65,
m2 65, m3 115, and
m4 115
F
ALGEBRA QRST is an isosceles trapezoid with median X
Y
.
Q
a. Find TS if QR 22 and XY 15.
1
3
a. Find DG if EF 20 and
MN 30. 40
Theorem 8.20
The median of a trapezoid is parallel to the bases,
and its measure is one-half the sum of the measures
of the bases.
Power
Point®
4
S
Multiply each side by 2.
Subtract 22 from each side.
b. Find m1, m2, m3, and m4 if m1 4a 10 and m3 3a 32.5.
Since QR
TS
, 1 and 3 are supplementary. Because this is an isosceles
trapezoid, 1 2 and 3 4.
Concept Check
Ask students to describe the
properties of an isosceles
trapezoid.
Exactly one pair of opposite sides is
parallel; the legs are congruent; each
pair of base angles is congruent; the
diagonals are congruent.
Consecutive Interior Angles Theorem
m1 m3 180
4a 10 3a 32.5 180
Substitution
7a 22.5 180
Combine like terms.
7a 157.5 Subtract 22.5 from each side.
a 22.5 Divide each side by 7.
If a 22.5, then m1 80 and m3 100.
Because 1 2 and 3 4, m2 80 and m4 100.
www.geometryonline.com/extra_examples
Lesson 8-6 Trapezoids 441
Geometry Activity
Materials: ruler, compass
Group students in pairs. Have each group draw a differently shaped trapezoid,
or provide pairs of different trapezoids for them to use.
Lesson 8-6 Trapezoids 441
3 Practice/Apply
Study Notebook
Have students—
• add the definitions/examples of
the vocabulary terms to their
Vocabulary Builder worksheets for
Chapter 8.
• include an example of a trapezoid
with the bases, legs, and median
labeled.
• include any other item(s) that they
find helpful in mastering the skills
in this lesson.
Concept Check
1. Exactly one pair
of opposite sides is
parallel.
2–3. See p. 459C.
Guided Practice
GUIDED PRACTICE KEY
Exercises
Examples
4–5
6
7
8
3
1
4
2
Assignment Guide
COORDINATE GEOMETRY QRST is a quadrilateral with vertices Q(3, 2),
R(1, 6), S(4, 6), T(6, 2).
QT
4. Verify that QRST is a trapezoid. R
S
and Q
R
S
T
, QRST is a trapezoid.
5. Determine whether QRST is an isosceles trapezoid. Explain.
isosceles, QR 20
, ST 20
6.
PROOF
CDFG is an isosceles trapezoid with bases CD
and F
G
.
Write a flow proof to prove DGF CFG. See p. 459C.
C
7. ALGEBRA EFGH is an isosceles trapezoid with bases E
F
and
H
and median Y
G
Z
. If EF 3x 8, HG 4x 10, and YZ 13,
find x. 4
About the Exercises…
Odd/Even Assignments
Exercises 9–38 are structured
so that students practice the
same concepts whether they
are assigned odd or even
problems.
2. Make a chart comparing the characteristics of the diagonals of a trapezoid, a
rectangle, a square, and a rhombus. (Hint: Use the types of quadrilaterals as
column headings and the properties of diagonals as row headings.)
3. OPEN ENDED Draw an isosceles trapezoid and a trapezoid that is not isosceles.
Draw the median for each. Is the median parallel to the bases in both trapezoids?
Application
Organization by Objective
• Properties of Trapezoids:
9–12, 20–38
• Medians of Trapezoids:
13–19, 39
1. List the minimum requirements to show that a quadrilateral is a trapezoid.
G
8. PHOTOGRAPHY Photographs can
show a building in a perspective that
makes it appear to be a different shape.
Identify the types of quadrilaterals in
the photograph. trapezoids,
★ indicates increased difficulty
Practice and Apply
For
Exercises
See
Examples
9–12, 23–32
13–19, 39
20–22, 38
33–37
3
4
2
1
Extra Practice
COORDINATE GEOMETRY For each quadrilateral whose vertices are given,
a. verify that the quadrilateral is a trapezoid, and
b. determine whether the figure is an isosceles trapezoid. 9–12. See margin.
9. A(3, 3), B(4, 1), C(5, 1), D(2, 3)
10. G(5, 4), H(5, 4), J(0, 5), K(5, 1)
11. C(1, 1), D(5, 3), E(4, 10), F(6, 0)
12. Q(12, 1), R(9, 4), S(4, 3), T(11, 4)
See page 770.
ALGEBRA Find the missing measure(s) for the given trapezoid.
13. For trapezoid DEGH, X and Y are
14. For trapezoid RSTV, A and B are
midpoints of the legs. Find VT. 4
midpoints of the legs. Find DE. 8
D
X
E
20
26
R
Y
S
15
A
B
32
Answers
442
Chapter 8 Quadrilaterals
F
parallelograms
Basic: 9–17 odd, 21–33 odd,
37, 39–61
Average: 9–39 odd, 40–61
Advanced: 10–38 even, 39–55
(optional: 56–61)
9a. A
D
|| BC
, CD ||⁄ AB
9b. not isosceles, AB 17
and
CD 5
10a. KJ || G
H
, KG ||⁄ JH
10b. not isosceles, GK 5, JH 26
11a. DC
|| FE, DE ||⁄ FC
11b. isosceles, DE 50, CF 50
12a. QR
|| TS
, QT ||⁄ RS
12b. isosceles, QT 26, RS 26
D
H
442
G
V
Chapter 8 Quadrilaterals
Tim Hall/PhotoDisc
Differentiated Instruction
Naturalist Challenge students to think of where they have seen
trapezoids in nature. Encourage students to research shapes of cells,
scales, and crystal faces for examples.
T
16. For trapezoid QRST, A and B are
midpoints of the legs. Find AB,
mQ, and mS. 16, 60, 135
W8Z
T
70˚
X
20
p. 447
(shown) and p. 448
Trapezoids
B
45˚
Q
R
2
1 (3)
1 (1)
0
slope of AD
0
7
4 (3)
0
33
slope of BC
0
3
2 (1)
1 3
4
slope of C
D
2
42
2
S
54
U
STUR is an isosceles trapezoid.
R
S
TU
; R U, S T
y
B
C
O
CD (2 4
)2 (
3 (
1))2
x
D
A
4 16
20
25
D
and BC
, so ABCD is a trapezoid. AB CD, so ABCD is
Exactly two sides are parallel, A
an isosceles trapezoid.
B
A
Q
T
leg
base
Example
Y
For Exercises 17 and 18, use trapezoid QRST.
17. Let G
H
be the median of RSBA. Find GH. 62
18. Let J
K be the median of ABTQ. Find JK. 78
base
S
R
The vertices of ABCD are A(3, 1), B(1, 3),
C(2, 3), and D(4, 1). Verify that ABCD is a trapezoid.2
AB (3 (1))
(
1 3
)2
3 (1)
4
slope of AB
2
4 16
20
25
R
20
____________ PERIOD _____
Properties of Trapezoids A trapezoid is a quadrilateral with
exactly one pair of parallel sides. The parallel sides are called bases
and the nonparallel sides are called legs. If the legs are congruent,
the trapezoid is an isosceles trapezoid. In an isosceles trapezoid
both pairs of base angles are congruent.
S
12
120˚
A
NAME ______________________________________________ DATE
Study
Guide
andIntervention
Intervention,
8-6
Study
Guide and
Lesson 8-6
15. For isosceles trapezoid XYZW,
find the length of the median,
mW, and mZ. 14, 110, 110
Exercises
In Exercises 1– 3, determine whether ABCD is a trapezoid. If so, determine
whether it is an isosceles trapezoid. Explain.
T
86
1. A(1, 1), B(2, 1), C(3, 2), and D(2, 2)
Slope of AB
0, slope of D
C
0, slope of A
D
1, slope of BC
3.
Exactly two sides are parallel, so ABCD is a trapezoid. AD 32
and
BC 10; AD BC, so ABCD is not isosceles.
★ 19. ALGEBRA JKLM is a trapezoid with JK
RP
L
M
and median .
1
Find RP if JK 2(x 3), RP 5 x, and ML x 1. 15
2. A(3, 3), B(3, 3), C(2, 3), and D(2, 3)
2
Slope of AB
0, slope of D
C
0, slope of B
C
6, slope of AD
6.
Exactly 2 sides are ||, so ABCD is a trapezoid. BC 37
and AD 37
;
BC AD, so ABCD is isosceles.
20. DESIGN The bagua is a tool used in Feng Shui design. This bagua consists
of two regular octagons centered around a yin-yang symbol. How can you
determine the type of quadrilaterals in the bagua? See margin.
3. A(1, 4), B(3, 3), C(2, 3), and D(2, 2)
1
4
1
4
Slope of AB
, slope of DC
, slope of BC
6, slope of AD
6.
Both pairs of opposite sides are parallel, so ABCD is not a trapezoid.
4. The vertices of an isosceles trapezoid are R(2, 2), S(2, 2), T(4, 1), and U(4, 1).
Verify that the diagonals are congruent.
Design
Feng Shui is an ancient
Chinese theory of design.
The goal is to create
spaces that enhance
creativity and balance.
Source: www.fengshui2000.com
RT ((4 (2))2
(
1 2
)2) 45
21. SEWING Madison is making a valance
for a window treatment. She is using
striped fabric cut on the bias, or diagonal,
to create a chevron pattern. Identify the
polygons formed in the fabric.
SU ((4 (2))2 (1
2)2) 45
Gl
NAME
______________________________________________
DATE
/M
G
Hill
447
Skills
Practice,
8-6
Practice
(Average)
____________
Gl PERIOD
G _____
p. 449 and
Practice,
Trapezoidsp. 450 (shown)
COORDINATE GEOMETRY RSTU is a quadrilateral with vertices R(3, 3), S(5, 1),
T(10, 2), U(4, 9).
parallelograms, trapezoids, hexagons, rectangles
1. Verify that RSTU is a trapezoid.
|| T
U
S
R
COORDINATE GEOMETRY Determine whether each figure is a trapezoid, a
parallelogram, a square, a rhombus, or a quadrilateral. Choose the most specific
term. Explain.
2. Determine whether RSTU is an isosceles trapezoid. Explain.
not isosceles; RU 37
and ST 34
COORDINATE GEOMETRY BGHJ is a quadrilateral with vertices B(9, 1), G(2, 3),
H(12, 2), J(10, 6).
parallelogram,
opp. sides ,
no rt. , no
cons. sides y
22.
C (4, 4)
B (1, 2)
23.
y
3. Verify that BGHJ is a trapezoid.
H (4, 2)
not isosceles; BJ 50
and GH 125
ALGEBRA Find the missing measure(s) for the given trapezoid.
D (5, 1)
O
4. Determine whether BGHJ is an isosceles trapezoid. Explain.
O
x
5. For trapezoid CDEF, V and Y are
midpoints of the legs. Find CD. 38
J (6, 1)
K (4, 1)
x
24.
y N (1, 3)
M (3, 1)
P (2, 2)
E
V
quadrilateral, 25.
opp. sides not
or y
Y
R (0, 3)
H
21
140
8. For isosceles trapezoid TVZY, find the
length of the median, mT, and mZ.
19.5, 60, 120
34
60
V
M
F
I
S (3, 0)
Y 5Z
9. CONSTRUCTION A set of stairs leading to the entrance of a building is designed in the
shape of an isosceles trapezoid with the longer base at the bottom of the stairs and the
shorter base at the top. If the bottom of the stairs is 21 feet wide and the top is 14, find
the width of the stairs halfway to the top. 17.5 ft
x
O
L
T
125
36
R
C
P
7. For trapezoid FGHI, K and M are
midpoints of the legs. Find FI, mF,
and mI. 51, 40, 55
G
66
42
B
D
K
Q (3, 0)
6. For trapezoid WRLP, B and C are
midpoints of the legs. Find LP. 18
W
28
C
x
O
18
F
E (2, 1)
23. trapezoid, exactly
one pair opp.
sides 25. square, all sides
, consecutive
sides || H
J
G
B
G (2, 2)
O (3, 1)
10. DESK TOPS A carpenter needs to replace several trapezoid-shaped desktops in a
classroom. The carpenter knows the lengths of both bases of the desktop. What other
measurements, if any, does the carpenter need?
T (0, 3)
Sample answer: the measures of the base angles
COORDINATE GEOMETRY For Exercises 26–28, refer
P (4, 3)
to quadrilateral PQRS.
26. Determine whether the figure is a trapezoid. If so,
is it isosceles? Explain. Q
R
PS, not isosceles, PQ RS
27. Find the coordinates of the midpoints of PQ
and R
S
,
and label them A and B. A(2, 3.5), B(4, 1)
28. Find AB without using the Distance Formula. 7.5
NAME
______________________________________________
DATE
/M
G
Hill
450
____________
Gl PERIOD
G _____
Reading
8-6
Readingto
to Learn
Learn Mathematics
y
Mathematics,
p. 451
Trapezoids
Q (0, 4)
Pre-Activity
R (4, 1)
ELL
How are trapezoids used in architecture?
Read the introduction to Lesson 8-6 at the top of page 439 in your textbook.
How might trapezoids be used in the interior design of a home?
Sample answer: floor tiles for a kitchen or bathroom
x
O
S (4, 3)
Reading the Lesson
1. In the figure at the right, EFGH is a trapezoid, I is the
midpoint of F
E
, and J is the midpoint of G
H
. Identify each
of the following segments or angles in the figure.
G
, EH
a. the bases of trapezoid EFGH F
F
I
E
G
J
H
b. the two pairs of base angles of trapezoid EFGH E and H; F and G
c. the legs of trapezoid EFGH F
E
, G
H
Lesson 8-6 Trapezoids 443
d. the median of trapezoid EFGH I
J
2. Determine whether each statement is true or false. If the statement is false, explain why.
a. A trapezoid is a special kind of parallelogram. False; sample answer: A
parallelogram has two pairs of parallel sides, but a trapezoid has only
one pair of parallel sides.
b. The diagonals of a trapezoid are congruent. False; sample answer: This is only
NAME ______________________________________________ DATE
Answers
20. Since the two octagons are regular
polygons with the same center, the
quadrilaterals are trapezoids with one pair
of opposite sides parallel.
8-6
Enrichment
Enrichment,
____________ PERIOD _____
true for isosceles trapezoids.
c. The median of a trapezoid is parallel to the legs. False; sample answer: The
p. 452
median is parallel to the bases.
d. The length of the median of a trapezoid is the average of the length of the bases.
true
Quadrilaterals in Construction
e. A trapezoid has three medians. False; sample answer: A trapezoid has only
one median.
Quadrilaterals are often used in construction work.
1. The diagram at the right represents a roof
frame and shows many quadrilaterals. Find
the following shapes in the diagram and
shade in their edges. See students’ work.
f. The bases of an isosceles trapezoid are congruent. False: sample answer: The
g. An isosceles trapezoid has two pairs of congruent angles.
ridge board
true
hip rafter
jack rafters
plate
a. isosceles triangle
b. scalene triangle
c. rectangle
d. rhombus
e. trapezoid (not isosceles)
f. isosceles trapezoid
legs are congruent.
valley rafter
common rafters
h. The median of an isosceles trapezoid divides the trapezoid into two smaller isosceles
trapezoids. true
Helping You Remember
Roof Frame
3. A good way to remember a new geometric theorem is to relate it to one you already
know. Name and state in words a theorem about triangles that is similar to the theorem
in this lesson about the median of a trapezoid. Triangle Midsegment Theorem; a
midsegment of a triangle is parallel to one side of the triangle, and its
length is one-half the length of that side.
Lesson 8-6 Trapezoids 443
Lesson 8-6
Gl
Answers
36. Given: ABCD is an isosceles
trapezoid.
C
B
|| A
D
B
A
CD
Prove: A D
ABC DCB
A
F
B
C
E
D
Proof: Draw auxiliary segments so
that BF ⊥ AD
and C
E ⊥ AD
. Since
B
C
|| A
D
and parallel lines are
everywhere equidistant, B
F CE.
Perpendicular lines form right
angles, so BFA and CED are
right angles. BFA and CED are
right triangles by definition.
Therefore, BFA CED by HL.
A D by CPCTC. Since CBF
and BCE are right angles and all
right angles are congruent,
CBF BCE. ABF DCE
by CPCTC. So, ABC DCB by
angle addition.
37. Sample answer:
D
29. DG
EF, D
E GF, COORDINATE GEOMETRY For Exercises 29–31, refer
to quadrilateral DEFG.
not isosceles,
DE GF
29. Determine whether the figure is a trapezoid. If so, is
it isosceles? Explain.
E and
30. Find the coordinates of the midpoints of D
F, and label them W and V.W(1.5, 3.5),V (1.5, 2.5)
G
31. Find WV without using the Distance Formula.
D (2, 2)
O
x
G (2, 2)
F (5, 3)
Write a flow proof. 32–35. See pp. 459C–459D.
G
K, HGK JKG, HG
JK
33. Given: TZX YXZ, W
X
Z
Y
32. Given: HJ Prove: GHJK is an isosceles trapezoid.
Prove: XYZW is a trapezoid.
PROOF
J
H
T
W
Z
1
G
2
K
Y
X
34. Given: ZYXP is an isosceles
trapezoid.
Prove: PWX is isosceles.
Y
X
★ 35. Given: E and C are midpoints
AD
DB
of A
D
and D
B
. Prove: ABCE is an isosceles
trapezoid.
W
D
P
E
Z
1 3
2
A
C
4
B
★ 36. Write a paragraph proof of Theorem 8.18. See margin.
CONSTRUCTION
Use a compass and ruler to construct each figure.
37. an isosceles trapezoid 37–38. See margin.
★ 38. trapezoid with a median 2 centimeters long
C
A
WV 6
You can use a map of
Seattle to locate and
draw a quadrilateral
that will help you begin
to find the hidden
treasure. Visit
www.geometry
online.com/webquest
to continue work on
your WebQuest project.
E (5, 5)
y
39. CRITICAL THINKING In RSTV, RS 6, VT 3,
and RX is twice the length of XV. Find XY. 4
B
38. Sample answer:
V
41. WRITING IN MATH
444 Chapter 8 Quadrilaterals
S
X
40. CRITICAL THINKING Is it possible for an isosceles
trapezoid to have two right base angles? Explain. See margin.
2 cm
40. It is not possible. Since pairs of
base angles of an isosceles
trapezoid are congruent, if two
angles are right, all four angles
will be right. Then the
quadrilateral would be a
rectangle, not a trapezoid.
41. Sample answer: Trapezoids are
used in monuments as well as
other buildings. Answers should
include the following.
• Trapezoids have exactly one
pair of opposite sides parallel.
• Trapezoids can be used as
window panes.
6
R
Y
T
3
Answer the question that was posed at the beginning of
the lesson. See margin.
How are trapezoids used in architecture?
Include the following in your answer:
• the characteristics of a trapezoid, and
• other examples of trapezoids in architecture.
Standardized
Test Practice
42. SHORT RESPONSE What type of quadrilateral is WXYZ?
Justify your answer.
W
Trapezoid; one pair of opp. sides is parallel.
Z
444 Chapter 8 Quadrilaterals
X
Y
43. ALGEBRA In the figure, which point lies within
the shaded region? B
A (2, 4)
B (1, 3)
C
(1, 3)
D
y
4 Assess
5
(2, 4)
–3 O
Open-Ended Assessment
X
Maintain Your Skills
Mixed Review
ALGEBRA In rhombus LMPQ, mQLM 2x2 10,
mQPM 8x, and MP 10. (Lesson 8-5)
44. Find mLPQ. 20
45. Find QL. 10
46. Find mLQP. 140 47. Find mLQM. 70
48. Find the perimeter of LMPQ. 40
Q
P
R
10
L
M
S y
COORDINATE GEOMETRY For Exercises 49–51,
refer to quadrilateral RSTV. (Lesson 8-4)
49. Find RS and TV. RS 72
, TV 113
50. (2, 1);
2, 32
Getting Ready for
Lesson 8-7
T
50. Find the coordinates of the midpoints of RT
and S
V
.
O
51. Is RSTV a rectangle? Explain. No; opposite sides
x
R
are not congruent and the diagonals do not bisect
each other.
V
Solve each proportion.
16
24
52. y 57
38
Getting Ready for
the Next Lesson
(Lesson 6-1)
y
17 17
53. 30 5
6
5
20
54. 3
y4
28
2y
52 13
55. 9
36 2
PREREQUISITE SKILL Write an expression for the slope of the segment given the
coordinates of the endpoints. (To review slope, see Lesson 3-3.)
56. (0, a), (a, 2a) 1
57. (a, b), (a, b) 0
58. (c, c), (c, d) undefined
2b
c
a 2b
59. (a, b), (2a, b) 60. (3a, 2b), (b, a) 61. (b, c), (b, c) a
b
3a b
P ractice Quiz 2
Quadrilateral ABCD is a rectangle.
1. Find x. 12
2. Find y. 5
Lessons 8-4 through 8-6
(Lesson 8-4)
A
(5x 5)˚
D
B
(2x 1)˚
(y 2 )˚
(3y 10)˚
Speaking Ask students to
describe each type of
quadrilateral. Ask them the
difference between
parallelograms, trapezoids, and
kites. Also ask them to
differentiate rectangles, rhombi,
and squares.
C
Prerequisite Skill Students will
learn about coordinate proofs in
Lesson 8-7. They will find the
slopes of segments on coordinate
planes. Use Exercises 56–61 to
determine your students’
familiarity with finding slopes
on coordinate planes.
Assessment Options
Practice Quiz 2 The quiz
provides students with a brief
review of the concepts and skills
in Lessons 8-4 through 8-6. Lesson
numbers are given to the right of
the exercises or instruction lines
so students can review concepts
not yet mastered.
Quiz (Lessons 8-5 and 8-6) is
available on p. 474 of the Chapter 8
Resource Masters.
3. COORDINATE GEOMETRY Determine whether MNPQ is a rhombus, a rectangle, or a square for
M(5, 3), N(2, 3), P(1, 3), and Q(2, 9). List all that apply. Explain. (Lesson 8-5)
rhombus, opp. sides , diag. , consec. sides not For trapezoid TRSV, M and N are midpoints of the legs.
4. If VS 21 and TR 44, find MN. 32.5
5. If TR 32 and MN 25, find VS. 18
(Lesson 8-6)
T
R
N
M
V
www.geometryonline.com/self_check_quiz
S
Lesson 8-6 Trapezoids 445
Lesson 8-6 Trapezoids 445
Reading
Mathematics
Hierarchy of Polygons
Getting Started
A hierarchy is a ranking of classes or sets of things. Examples of some classes of
polygons are rectangles, rhombi, trapezoids, parallelograms, squares, and
quadrilaterals. These classes are arranged in the hierarchy below.
You may want to give groups of
students the categories detailed in
the hierarchy on the student page
as cutouts in an envelope before
referring to the textbook. Ask the
groups to agree on the
arrangement of the hierarchy, then
use the textbook to check their
result. Each group should be able
to justify the order they decide on.
Polygons
Quadrilaterals
Parallelograms
Teach
Rectangles
Hierarchy of Polygons In this
activity, students will learn that
each class is linked to the class
above it in the hierarchy. For
example, every square is a
rectangle, but not every rectangle
is a square. Also, rectangles,
rhombi, and squares are all
parallelograms. Make sure
students understand that they
should follow the direction of
the arrows on the chart.
Use the following information to help read the hierarchy diagram.
For example, polygons is the broadest class in the hierarchy diagram above, and
squares is a very specific class.
• Each class is contained within any class linked above it in the hierarchy. For example,
all squares are also rhombi, rectangles, parallelograms, quadrilaterals, and polygons.
However, an isosceles trapezoid is not a square or a kite.
• Some, but not all, elements of each class are contained within lower classes in the
hierarchy. For example, some trapezoids are isosceles trapezoids, and some rectangles
are squares.
Reading to Learn
Bips
Refer to the hierarchy diagram at the right. Write true, false, or
not enough information for each statement.
1. All mogs are jums. false
Mogs
2. Some jebs are jums. false
3. All lems are jums. true
Ask students to summarize what they
have learned about quadrilaterals,
parallelograms, trapezoids, and kites
in their notebooks.
4. Some wibs are jums. true
Jebs
Jums
5. All mogs are bips. true
6. Draw a hierarchy diagram to show these classes: equilateral
triangles, polygons, isosceles triangles, triangles, and scalene
triangles. See margin.
446 Chapter 8 Quadrilaterals
Answer
6.
Polygons
Triangles
Isosceles
Equilateral
Chapter 8 Quadrilaterals
Isosceles
Trapezoids
• The class that is the broadest is listed first, followed by the other classes in order.
Study Notebook
446
Rhombi
Trapezoids
Squares
Assess
ELL English Language
Learners may benefit from
writing key concepts from this
activity in their Study Notebooks
in their native language and then
in English.
Kites
Scalene
Wibs
Lems
446 Investigating
Coordinate Proof
With Quadrilaterals
Lesson
Notes
• Position and label quadrilaterals for use in coordinate proofs.
1 Focus
• Prove theorems using coordinate proofs.
can you use a coordinate plane to
prove theorems about quadrilaterals?
In Chapter 4, you learned that variable coordinates can
be assigned to the vertices of triangles. Then the Distance
and Midpoint Formulas and coordinate proofs were used
to prove theorems. The same is true for quadrilaterals.
5-Minute Check
Transparency 8-7 Use as a
quiz or review of Lesson 8-6.
y
Mathematical Background notes
are available for this lesson on
p. 402D.
x
O
POSITION FIGURES The first step to using a coordinate proof is to place the
figure on the coordinate plane. The placement of the figure can simplify the steps
of the proof.
Study Tip
Positioning a Square
Example 1
Look Back
To review placing a figure
on a coordinate plane,
see Lesson 4-7.
Position and label a square with sides a units long on the coordinate plane.
• Let A, B, C, and D be vertices of a square with sides a units long.
• Place the square with vertex A at the origin, A
B
along the positive x-axis, and
AD
along the y-axis. Label the vertices A, B, C, and D.
• The y-coordinate of B is 0 because the vertex is on the
x-axis. Since the side length is a, the x-coordinate is a.
y
C (a, a)
D (0, a)
• D is on the y-axis so the x-coordinate is 0. The
y-coordinate is 0 a or a.
• The x-coordinate of C is also a. The y-coordinate is 0 a
or a because the side B
C
is a units long.
O A(0, 0) B(a, 0) x
can you use a coordinate
plane to prove theorems
about quadrilaterals?
Ask students:
• What is a convenient location
to place a square on the
coordinate plane? with one
vertex at (0, 0) and one side along
the x-axis
• What is usually the best
position to place a figure on
the coordinate plane? Sample
answer: with one side parallel to
an axis and one vertex at (0, 0)
• What formulas have been used
in the past in coordinate proofs?
Distance Formula; Slope Formula;
Midpoint Formula
Some examples of quadrilaterals placed on the coordinate plane are given below.
Notice how the figures have been placed so the coordinates of the vertices are as
simple as possible.
y
(0, a)
y
y
(b, a)
a
O (0, 0) b (b, 0) x
rectangle
y
(a, b) (c – a, b)
(b, c) (a + b, c)
c
c
b
b
O (0, 0) (a, 0) x
b
a
O (0, 0)
parallelogram
b
a
(c, 0) x
isosceles trapezoid
(b, c) (a + b, c)
O (0, 0) (a, 0)
x
rhombus
Lesson 8-7 Coordinate Proof with Quadrilaterals 447
Resource Manager
Workbook and Reproducible Masters
Chapter 8 Resource Masters
• Study Guide and Intervention, pp. 453–454
• Skills Practice, p. 455
• Practice, p. 456
• Reading to Learn Mathematics, p. 457
• Enrichment, p. 458
• Assessment, p. 474
Teaching Geometry With Manipulatives
Masters, pp. 2, 8, 138
Transparencies
5-Minute Check Transparency 8-7
Answer Key Transparencies
Technology
Interactive Chalkboard
Multimedia Applications: Virtual Activities
Lesson x-x Lesson Title 447
Example 2 Find Missing Coordinates
2 Teach
The length of A
B
is b, and the length of D
C
is b.
So, the x-coordinate of D is (b c) b or c.
Power
Point®
Position and label a rectangle
with sides a and b units long
on the coordinate plane.
Sample
y
D(0, b) C(a, b)
answer:
O A(0, 0) B(a, 0) x
• Use The Geometer’s Sketchpad
to draw a quadrilateral ABCD
with no two sides parallel or
congruent.
• Construct the midpoints of
each side.
• Draw the quadrilateral
formed by the midpoints
of the segments.
for the isosceles trapezoid.
D(b, c)
y
D (?, ?) C (a 2b, c)
B(a, 0) x
M
Q
B (0, –2b)
Place rhombus ABCD on the
coordinate plane so that the origin
is the midpoint of the diagonals
and the diagonals are on the axes,
as shown.
Given: ABCD is a rhombus as
labeled. M, N, P, Q are
midpoints.
Prove: MNPQ is a rectangle.
The coordinates of M are
(a, b); the coordinates of N
are (a, b); the coordinates of P
are (a, b); the coordinates of Q
are (a, b). Slope of MQ
0;
slope of Q
P undefined; slope of
N 0; slope of N
M undefined.
P
A segment with slope 0 is perpendicular to a segment with undefined slope. Therefore, consecutive
sides of this quadrilateral are
perpendicular. Since consecutive
sides are perpendicular, MNPQ
is, by definition, a rectangle.
448
Chapter 8 Quadrilaterals
D
C
Parallelogram; the opposite sides are congruent.
In this activity, you discover that the quadrilateral formed from the midpoints of any
quadrilateral is a parallelogram. You will prove this in Exercise 22.
y
C (2a, 0) x
B
A
1. Measure each side of the quadrilateral determined by the midpoints
of ABCD. See students’ work.
2. What type of quadrilateral is formed by the midpoints? Justify your answer.
coordinate plane. Label the
midpoints of the sides M, N,
P, and Q. Write a coordinate
proof to prove that MNPQ is
a rectangle.
O
x
Analyze
3 Place a rhombus on the
A(–2a, 0)
B (b, 0)
Quadrilaterals
Model
2 Name the missing coordinates
N
O A (0, 0)
PROVE THEOREMS Once a figure has been placed on the coordinate plane,
we can prove theorems using the Slope, Midpoint, and Distance Formulas.
Quadrilaterals
D (0, 2b)
P
C (b + c, a)
The coordinates of D are (c, a).
1 POSITIONING A RECTANGLE
A(0, 0)
D (?, ?)
Name the missing coordinates for the parallelogram.
Opposite sides of a parallelogram are congruent and
parallel. So, the y-coordinate of D is a.
POSITION FIGURES
In-Class Examples
y
Example 3 Coordinate Proof
Study Tip
Place a square on a coordinate plane. Label the midpoints of the sides,
M, N, P, and Q. Write a coordinate proof to prove that MNPQ is a square.
Problem Solving
To prove that a
quadrilateral is a square,
you can also show that
all sides are congruent
and that the diagonals
bisect each other.
y
The first step is to position a square on the coordinate
plane. Label the vertices to make computations as
simple as possible.
D (0, 2a)
Given: ABCD is a square.
M, N, P, and Q are midpoints.
P (a, 2a)
Q (0, a)
C (2a, 2a)
N (2a, a)
Prove: MNPQ is a square.
A(0, 0)
M (a, 0) B (2a, 0) x
Proof:
By the Midpoint Formula, the coordinates of M, N, P, and Q are as follows.
2a 0 0 0
2
2
M , (a, 0)
0 2a 2a 2a
2
2
P , (a, 2a)
2a 2a 2a 0
2
2
N , (2a, a)
0 0 0 2a
2
2
Q , (0, a)
448 Chapter 8 Quadrilaterals
Geometry Software Investigation
• Have students drag one or more of the vertices to create a different
quadrilateral. Analyze the new quadrilateral.
• This activity can be repeated with different quadrilaterals. Investigate the
quadrilateral formed by the midpoints of the sides of a square, a
rhombus, or a trapezoid.
Find the slopes of QP
MN
, , Q
M
, and P
N
.
PROVE THEOREMS
a0
2a a
2a a
a0
slope of QP
or 1
slope of M
N
or 1
a0
0a
In-Class Example
2a a
a 2a
slope of QM
or 1
slope of PN
or 1
4 Write a coordinate proof to
Each pair of opposite sides is parallel, so they have the same slope. Consecutive
sides form right angles because their slopes are negative reciprocals.
prove that the supports of a
platform lift are parallel.
Use the Distance Formula to find the length of QP
and Q
M
.
(a (2
a QP 0)2
y
QM (a (0
a)2
0)2
a)2
a2 a2
a2 a2
or a2
or a2
2a2
C (5, 10)
D (0, 5)
2a2
MNPQ is a square because each pair of opposite sides is parallel, and consecutive
sides form right angles and are congruent.
PARKING Write a coordinate proof to prove that
the sides of the parking space are parallel.
y
Given: 14x 6y 0; 7x 3y 56
D
C
14x 6y 0
BC
Prove: AD
O
A
Proof: Rewrite both equations in slope-intercept form.
14x 6y 0
7x 3y 56
B
x
7x 3y 56
3y 7x 56
3
3
7
56
y x 3
3
7
y 3x
1. Explain how to position a quadrilateral to simplify the steps of the proof.
2. OPEN ENDED
Position and label a trapezoid with two vertices on the y-axis.
1– 2. See p. 459D.
Guided Practice
GUIDED PRACTICE KEY
Exercises
Examples
3
4–5
6–7
8
1
2
3
4
Position and label the quadrilateral on the coordinate plane.
3. rectangle with length a units and height a b units See p. 459D.
Name the missing coordinates for each quadrilateral.
y
(a, a)
5. y
4.
D (0, a)
D(?, ?)
C (?, ?)
A(5, 0) x
3 Practice/Apply
Study Notebook
Since AD
and B
C
have the same slope, they are parallel.
Concept Check
B(10, 5)
Given: A(5, 0), B(10, 5),
C(5, 10), and D(0, 5).
B
|| C
D
Prove: A
Slope of A
B 1. Slope of C
D1
Since AB
and CD
have the same
slope, they are parallel.
Example 4 Properties of Quadrilaterals
6y
14x
6
6
Power
Point®
Have students—
• add the definitions/examples of
the vocabulary terms to their
Vocabulary Builder worksheets for
Chapter 8.
• include any other item(s) that they
find helpful in mastering the skills
in this lesson.
(c, b)
C (a + c, b)
About the Exercises…
O A(0, 0) B(a, 0) x
O A (0, 0)
B (a, 0)
Organization by Objective
• Position Figures: 9–16, 23
• Prove Theorems: 17–22,
24–26
x
Write a coordinate proof for each statement. 6– 7. See p. 459D.
6. The diagonals of a parallelogram bisect each other.
7. The diagonals of a square are perpendicular.
www.geometryonline.com/extra_examples
Lesson 8-7 Coordinate Proof with Quadrilaterals 449
Differentiated Instruction
Interpersonal Students may benefit from going on a short walk
around the school campus with other geometry students to photograph
or sketch examples of quadrilaterals in the real world. As they discover
quadrilaterals, ask them to discuss how they can separate the
quadrilaterals into the classes studied in this chapter.
Odd/Even Assignments
Exercises 9–22 are structured
so that students practice the
same concepts whether they
are assigned odd or even
problems.
Assignment Guide
Basic: 9–19 odd, 23, 25, 27–39
Average: 9–27 odd, 28–39
Advanced: 10–22 even, 23, 24,
26, 27–39
Lesson 8-7 Coordinate Proof with Quadrilaterals 449
NAME ______________________________________________ DATE
Application
____________ PERIOD _____
Study
Guide
andIntervention
Intervention,
8-7
Study
Guide and
8. STATES The state of Tennessee can be separated into two shapes that resemble
quadrilaterals. Write a coordinate proof to prove that DEFG is a trapezoid. All
measures are approximate and given in kilometers. See p. 459D.
p. 453
(shown)
p. 454
Coordinate
Proof withand
Quadrilaterals
Position Figures Coordinate proofs use properties of lines and segments to prove
geometric properties. The first step in writing a coordinate proof is to place the figure on the
coordinate plane in a convenient way. Use the following guidelines for placing a figure on
the coordinate plane.
D
(195, 180)
1. Use the origin as a vertex, so one set of coordinates is (0, 0), or use the origin as the center of the figure.
(765, 180) E
2. Place at least one side of the quadrilateral on an axis so you will have some zero coordinates.
TENNESSEE
4. Use coordinates that make the computations as easy as possible. For example, use even numbers if you
are going to be finding midpoints.
Example
Position and label a rectangle with sides a
and b units long on the coordinate plane.
y
T (b, a)
S (0, a)
• Place one vertex at the origin for R, so one vertex is R(0, 0).
• Place side RU
along the x-axis and side RS
along the y-axis,
with the rectangle in the first quadrant.
• The sides are a and b units, so label two vertices S(0, a) and
U(b, 0).
• Vertex T is b units right and a units up, so the fourth vertex is T(b, a).
U(b, 0) x
R(0, 0)
Lesson 8-7
3. Try to keep the quadrilateral in the first quadrant so you will have positive coordinates.
G (195, 0)
★ indicates increased difficulty
Practice and Apply
Exercises
Position and label each quadrilateral on the coordinate plane. 9–10. See margin.
Name the missing coordinates for each quadrilateral.
1.
2.
y
x
A(0, 0) B (c, 0)
3.
y
N(?, ?)
C(?, ?)
D(0, c)
M(0, 0)
C(c, c)
y
B(b, ?)
P(a b, c)
Q(a, 0) x
C(?, c)
x
A(0, 0) D(a, 0)
B(b, c); C(a b, c)
N(b, c)
Position and label each quadrilateral on the coordinate plane. Sample answers
are given.
4. square STUV with
side s units
5. parallelogram PQRS
with congruent diagonals
6. rectangle ABCD with
length twice the width
y
y
T(0, s)
U(s, s)
y
Q (0, b)
R(a, b)
B(0, a)
For
Exercises
See
Examples
9–10
11–16, 23
17–22
24–26
1
2
3
4
9. isosceles trapezoid with height c units, bases a units and a 2b units
10. parallelogram with side length c units and height b units
Name the missing coordinates for each parallelogram or trapezoid.
y
B(b, c)
12.
A(b, b),
11.
y
Extra Practice
C (2a, a)
A (?, ?)
See page 771.
x
S(0, 0) V(s, 0)
P(0, 0)
F (533, 0)
S(a, 0) x
A(0, 0)
D(2a, 0) x
E(b, b)
C (b, b)
C (a, c)
B (?, ?)
x
O
NAME
______________________________________________
DATE
/M
G
Hill
453
Gl
____________
Gl PERIOD
G _____
Skills
Practice,
p. 455 and
8-7
Practice
(Average)
Practice,
456
Coordinatep.
Proof
with (shown)
Quadrilaterals
G (b, b)
O H (0, 0) G (a + b, 0) x
E (?, ?)
Position and label each quadrilateral on the coordinate plane.
1. parallelogram with side length b units
and height a units
13.
2. isosceles trapezoid with height b units,
bases 2c a units and 2c a units
G(a, 0),
E(b, c)
y
y
y
D(a, b) C(2c, b)
C(b c, a)
D(c, a)
F(a b, c)
E(?, ?)
Name the missing coordinates for each quadrilateral.
3. parallelogram
y
L(c, ?)
K(?, a)
O H(0, 0)
J (2b, 0) x
Y(?, ?)
x
Z(b, c)
X(?, ?) O
K(2b c, a), L(c, a)
L(a + b, c)
O J (0, 0) K (a, 0)
G(?, ?) x
O H(0, 0)
4. isosceles trapezoid
y
M(b, c)
y
M (?, ?)
B(a 2c, 0) x
O A(0, 0)
B(b, 0) x
O A(0, 0)
14.
15.
W(a, 0) x
X(a, 0), Y(b, c)
y
U (2a, c)
T (?, ?)
Position and label the figure on the coordinate plane. Then write a coordinate
proof for the following.
T(2a, c),
W(2a, c)
16.
y
(
1
Q 0, 2 a
)
R (a, a – c)
1
2
T 0, a ,
S(a, a c)
5. The opposite sides of a parallelogram are congruent.
Given: ABCD is a parallelogram.
CD
, AD
BC
Prove: AB
Proof:
C(a b, c)
D(b, c)
x
O
y
W (?, ?)
(a 0
)2 (
0 0
)2 a 2 or a
AB V (2a, –c)
O
T (?, ?)
B(a, 0) x
O A(0, 0)
x
S (?, ?)
[(a b) b
]2 (
c c
)2 a 2 or a
CD (b 0
)2 (
c 0
)2 b2 c2
AD AB [(a b) a
]2 (c
0)2 b2 c2
AB CD and AD BC, so AB
CD
and A
D
BC
6. THEATER A stage is in the shape of a trapezoid. Write a
coordinate proof to prove that T
R
and S
F
are parallel.
Position and label each figure on the coordinate plane. Then write a coordinate
proof for each of the following. 17–22. See pp. 459D– 459E.
y
S(30, 25)
F(0, 25)
Given: T(10, 0), R(20, 0), S(30, 25), F(0, 25)
|| S
F
Prove: TR
17. The diagonals of a rectangle are congruent.
00
0
20 10
10
25 25
0
the slope of SF . Since TR
and
30 0
30
Proof: The slope of TR
and
SF
both have a slope of 0, T
R
O T(10, 0) R(20, 0)
18. If the diagonals of a parallelogram are congruent, then it is a rectangle.
|| S
F
.
NAME
______________________________________________
DATE
/M
G
Hill
456
Gl
x
19. The diagonals of an isosceles trapezoid are congruent.
____________
Gl PERIOD
G _____
Reading
8-7
Readingto
to Learn
Learn Mathematics
20. The median of an isosceles trapezoid is parallel to the bases.
ELL
Mathematics,
p. 457
Coordinate Proof with Quadrilaterals
Pre-Activity
★ 21. The segments joining the midpoints of the sides of a rectangle form a rhombus.
★ 22. The segments joining the midpoints of the sides of a quadrilateral form a
How can you use a coordinate plane to prove theorems about
quadrilaterals?
Read the introduction to Lesson 8-7 at the top of page 447 in your textbook.
What special kinds of quadrilaterals can be placed on a coordinate system so
that two sides of the quadrilateral lie along the axes?
parallelogram.
rectangles and squares
Reading the Lesson
1. Find the missing coordinates in each figure. Then write the coordinates of the four
vertices of the quadrilateral.
a. isosceles trapezoid
★ 23. CRITICAL THINKING A has coordinates (0, 0), and B has coordinates (a, b).
b. parallelogram
y
y
S(?, c)
Find the coordinates of C and D so ABCD is an isosceles trapezoid.
P (?, c a)
T (b, ?)
N (?, a)
Q (b, ?)
R (?, ?)
U(a, ?) x
O
R(a, 0), S(b, c), T(b, c), U(a, 0)
O M (?, ?)
450 Chapter 8 Quadrilaterals
x
M(0, 0), N(0, a), P(b, c a), Q(b, c)
2. Refer to quadrilateral EFGH.
F
3,
a. Find the slope of each side. slope E
1
3
y
G
F
1
3
slope F
G
, slope GH
3, slope HE
NAME ______________________________________________ DATE
H
x
E
d.
e.
f.
EF 10
, FG 10
, GH 10
, HE 10
Find the slope of each diagonal. slope E
G
1, slope F
H
1
Find the length of each diagonal. EG 32, FH 8
What can you conclude about the sides of EFGH? All four sides are congruent
and both pairs of opposite sides are parallel.
What can you conclude about the diagonals of EFGH? The diagonals are
perpendicular and they are not congruent.
g. Classify EFGH as a parallelogram, a rhombus, or a square. Choose the most specific
term. Explain how your results from parts a-f support your conclusion.
EFGH is a rhombus. All four sides are congruent and the diagonals
are perpendicular. Since the diagonals are not congruent, EFGH is not
a square.
Helping You Remember
3. What is an easy way to remember how best to draw a diagram that will help you devise
a coordinate proof? Sample answer: A key point in the coordinate plane is
the origin. The everyday meaning of origin is place where something
begins. So look to see if there is a good way to begin by placing a vertex
of the figure at the origin.
450
Chapter 8 Quadrilaterals
____________ PERIOD _____
O
b. Find the length of each side.
c.
Sample answer: C(a c, b), D(2a c, 0)
8-7
Enrichment
Enrichment,
p. 458
Coordinate Proofs
An important part of planning a coordinate proof is correctly placing and labeling the
geometric figure on the coordinate plane.
Example
Draw a diagram you would use in a coordinate proof of the
following theorem.
The median of a trapezoid is parallel to the bases of the trapezoid.
y
In the diagram, note that one vertex, A, is placed at the origin. Also,
the coordinates of B, C, and D use 2a, 2b, and 2c in order to avoid
the use of fractions when finding the coordinates of the midpoints,
M and N.
M
When doing coordinate proofs, the following strategies may be helpful.
B(2b, 2c)
C(2d, 2c)
O A(0, 0)
1. If you are asked to prove that segments are parallel or perpendicular, use slopes.
2. If you are asked to prove that segments are congruent or have related measures,
use the distance formula.
3. If you are asked to prove that a segment is bisected, use the midpoint formula.
N
D(2a, 0) x
ARCHITECTURE For Exercises 24–26, use the following information.
The Leaning Tower of Pisa is approximately 60 meters tall, from base to belfry.
The tower leans about 5.5° so the top level is 4.5 meters over the first level.
4 Assess
24. Position and label the tower on a coordinate plane. 24–26. See margin.
25. Is it possible to write a coordinate proof to prove that the sides of the tower are
parallel? Explain.
26. From the given information, what conclusion can be drawn?
Open-Ended Assessment
Writing Ask students to describe
how to position each type of
quadrilateral on the coordinate
plane so that the coordinates of
the vertices are as simple as
possible.
Answer the question that was posed at the beginning of
the lesson. See margin.
How is the coordinate plane used in proofs?
27. WRITING IN MATH
Architecture
The tower is also sinking.
In 1838, the foundation
was excavated to reveal
the bases of the columns.
Include the following in your answer:
• guidelines for placing a figure on a coordinate grid, and
• an example of a theorem from this chapter that could be proved using the
coordinate plane.
Source: www.torre.duomo.pisa.it
Standardized
Test Practice
28. In the figure, ABCD is a parallelogram.
What are the coordinates of point D? D
A (a, c b)
B (c b, a)
C
(b c, a)
D
y
A (0, a)
D
D
C (c , 0 ) x
B (b, 0 )
O
10
Quiz (Lesson 8-7) is available on
p. 474 of the Chapter 8 Resource
Masters.
(c b, a)
29. ALGEBRA If p 5, then 5 p2 p A 15
B 5
C
Assessment Options
? . A
30
Maintain Your Skills
Mixed Review
30. PROOF Write a two-column proof. (Lesson 8-6)
Given: MNOP is a trapezoid with bases MN
and O
P
.
M
N
Q
O
Prove: MNOQ is a parallelogram. See margin.
P
Q
O
M
JKLM is a rectangle. MLPR is a rhombus. JMK RMP,
mJMK 55, and mMRP 70. (Lesson 8-5)
31. Find mMPR. 55
32. Find mKML. 35
33. Find mKLP. 160
N
J
K
M
L
R
P
Find the geometric mean between each pair of numbers. (Lesson 7-1)
34. 7 and 14 98
35. 25 and 65 60
9.9
7.7
Write an expression relating the given pair of angle
measures. (Lesson 5-5)
36. mWVX, mVXY mWVX mVXY
37. mXVZ, mVXZ mXVZ mVXZ
38. mXYV, mVXY mXYV mVXY
39. mXZY, mZXY mXZY mZXY
www.geometryonline.com/self_check_quiz
W
9
X
12
8
9
6
V
6
Z
6.1
27. Sample answer: The coordinate
plane is used in coordinate
proofs. The Distance Formula,
Midpoint Formula and Slope
Formula are used to prove
theorems. Answers should include
the following.
• Place the figure so one of the
vertices is at the origin. Place
at least one side of the figure on
the positive x-axis. Keep the
figure in the first quadrant if
possible and use coordinates
that will simplify calculations.
• Sample answer: Theorem 8.3
Opposite sides of a
parallelogram are congruent.
30. Given: MNOP is a trapezoid with
bases MN
and O
P
.
MN
QO
Prove: MNOQ is a parallelogram.
Y
Q
P
Lesson 8-7 Coordinate Proof with Quadrilaterals 451
O
Paul Trummer/Getty Images
M
Answers
24.
y
D(c, d )
C(a 4.5, b)
O
A(0, 0)
B(a, 0)
x
25. No, there is not enough information given to prove that the
sides of the tower are parallel.
26. From the information given, we can approximate the height
from the ground to the top level of the tower.
N
Proof:
Statements (Reasons)
1. MNOP is a trapezoid with bases
N
M
and O
P
; M
N
QO
(Given)
2. O
P
|| M
N
(Def. of a trapezoid.)
3. MNOQ is a parallelogram. (If
one pair of opp. sides are || and
, the quad. is a .)
Lesson 8-7 Coordinate Proof with Quadrilaterals 451
Study Guide
and Review
Vocabulary and Concept Check
Vocabulary and
Concept Check
• This alphabetical list of
vocabulary terms in Chapter 8
includes a page reference
where each term was
introduced.
• Assessment A vocabulary
test/review for Chapter 8 is
available on p. 472 of the
Chapter 8 Resource Masters.
Lesson-by-Lesson
Review
For each lesson,
• the main ideas are
summarized,
• additional examples review
concepts, and
• practice exercises are provided.
Vocabulary
PuzzleMaker
diagonal (p. 404)
isosceles trapezoid (p. 439)
kite (p. 438)
Exercises State whether each sentence is true or false. If false, replace the
underlined term to make a true sentence.
1. The diagonals of a rhombus are perpendicular. true
2. All squares are rectangles. true
3. If a parallelogram is a rhombus , then the diagonals are congruent. false; rectangle
4. Every parallelogram is a quadrilateral. true
5. A(n) rhombus is a quadrilateral with exactly one pair of parallel sides. false; trapezoid
6. Each diagonal of a rectangle bisects a pair of opposite angles. false; rhombus
7. If a quadrilateral is both a rhombus and a rectangle, then it is a square . true
8. Both pairs of base angles in a(n) isosceles trapezoid are congruent. true
8-1 Angles of Polygons
See pages
404–409.
Example
Find the measure of an interior angle of a regular decagon.
Interior Angle Sum Theorem
180(10 2)
n 10
180(8) or 1440
Simplify.
The measure of each interior angle is 1440 10, or 144.
Exercises Find the measure of each interior angle of a regular polygon given
the number of sides. See Example 1 on page 405.
9. 6 120
10. 15 156
11. 4 90
12. 20 162
ALGEBRA Find the measure of each interior angle. See Example 3 on page 405.
C (x 25)˚
X
mA 105,
13.
14.
mW 62,
a˚
mB 120,
Y mX 108,
D
(a 28)˚
mY
80,
(
)
B (1.5x 3)˚
2x 22 ˚ mC 103,
( 12 a 8((˚a 2)
mD 134,
mZ
110
˚
(x 27)˚ x
W
˚
mE 78
MindJogger
Videoquizzes
Z
452 Chapter 8 Quadrilaterals
Round 1 Concepts (5 questions)
Round 2 Skills (4 questions)
Round 3 Problem Solving (4 questions)
A
E
www.geometryonline.com/vocabulary_review
TM
For more information
about Foldables, see
Teaching Mathematics
with Foldables.
Chapter 8 Quadrilaterals
Concept Summary
• If a convex polygon has n sides and the sum of the measures of its interior
angles is S, then S 180(n 2).
• The sum of the measures of the exterior angles of a convex polygon is 360.
S 180(n 2)
The Vocabulary PuzzleMaker
software improves students’ mathematics
vocabulary using four puzzle formats—
crossword, scramble, word search using a
word list, and word search using clues.
Students can work on a computer screen
or from a printed handout.
452
rhombus (p. 431)
square (p. 432)
trapezoid (p. 439)
A complete list of postulates and theorems can be found on pages R1–R8.
ELL
ELL MindJogger Videoquizzes
provide an alternative review of concepts
presented in this chapter. Students work
in teams in a game show format to gain
points for correct answers. The questions
are presented in three rounds.
median (p. 440)
parallelogram (p. 411)
rectangle (p. 424)
Have students look through the chapter to make sure they have
included notes and examples in their Foldables for each lesson of
Chapter 8.
Encourage students to refer to their Foldables while completing
the Study Guide and Review and to use them in preparing for the
Chapter Test.
Chapter 8 Study Guide and Review
Study Guide and Review
8-2 Parallelograms
See pages
411–416.
Example
Concept Summary
• In a parallelogram, opposite sides are parallel and congruent, opposite
angles are congruent, and consecutive angles are supplementary.
• The diagonals of a parallelogram bisect each other.
WXYZ is a parallelogram.
Find mYZW and mXWZ.
mYZW mWXY
mYZW 82 33 or 115
mXWZ mWXY 180
mXWZ (82 33) 180
mXWZ 115 180
mXWZ 65
Exercises
X
Opp.
of are .
Y
33˚
82˚
W
Z
mWXY mWXZ mYXZ
Cons.
in are suppl.
mWXY mWXZ mYXZ
Simplify.
Subtract 115 from each side.
Use ABCD to find each measure.
20˚ A
See Example 2 on page 413.
9
15. mBCD 52
17. mBDC 87.9
19. CD 6
D
16. AF 6.86
18. BC 9
20. mADC 128
6
F
32˚
B
6.86
40.1˚
C
8-3 Tests for Parallelograms
See pages
417–423.
Concept Summary
A quadrilateral is a parallelogram if any one of the following is true.
•
•
•
•
Example
Both pairs of opposite sides are parallel and congruent.
Both pairs of opposite angles are congruent.
Diagonals bisect each other.
A pair of opposite sides is both parallel and congruent.
COORDINATE GEOMETRY Determine whether the figure with vertices
A(5, 3), B(1, 5), C(6, 1), and D(2, 1) is a parallelogram. Use the
Distance and Slope Formulas.
B y
[5 (1)]2
(3
5)2
AB A
2
(4)
(2
)2 or 20
CD (6 2
)2 [1
(1
)]2
C
42 22 or 20
x
O
D
Since AB CD, AB
CD
.
53
1 (5)
1
2
slope of AB
or 1 1
26
1
2
slope of CD
or A
B
and C
D
have the same slope, so they are parallel. Since one pair of
opposite sides is congruent and parallel, ABCD is a parallelogram.
Chapter 8 Study Guide and Review 453
Chapter 8 Study Guide and Review 453
Study Guide and Review
Chapter 8 Study Guide and Review
Exercises Determine whether the figure with the given vertices is a
parallelogram. Use the method indicated. See Example 5 on page 420.
21. A(2, 5), B(4, 4), C(6, 3), D(1, 2); Distance Formula no
22. H(0, 4), J(4, 6), K(5, 6), L(9, 4); Midpoint Formula yes
23. S(2, 1), T(2, 5), V(10, 13), W(14, 7); Slope Formula yes
8-4 Rectangles
See pages
424–430.
Example
Concept Summary
• A rectangle is a quadrilateral with four right angles and congruent
diagonals.
• If the diagonals of a parallelogram are congruent, then the parallelogram
is a rectangle.
Quadrilateral KLMN is a rectangle.
If PL x2 1 and PM 4x 11, find x.
The diagonals of a rectangle are congruent and
PM
bisect each other, so PL
.
L P
P
M
PL PM
x2
M
x 1
2
4x 11
P
K
N
Diag. are and bisect each other.
Def. of angles
1 4x 11 Substitution
x2 1 4x 11
Subtract 4x from each side.
4x 12 0
Subtract 11 from each side.
x2
L
(x 2)(x 6) 0
Factor.
x20
x60
x 2
x6
The value of x is 2 or 6.
Exercises
ABCD is a rectangle.
A
1
2
See Examples 1 and 2 on pages 425 and 426.
24. If AC 9x 1 and AF 2x 7, find AF. 13
25. If m1 12x 4 and m2 16x 12, find m2. 52 D
4
5
3
6
B
F
C
26. If CF 4x 1 and DF x 13, find x. 4
27. If m2 70 4x and m5 18x 8, find m5. 28
COORDINATE GEOMETRY Determine whether RSTV is a rectangle given each set
of vertices. Justify your answer. See Example 4 on pages 426 and 427.
28. R(3, 5), S(0, 5), T(3, 4), V(0, 4) No, consec. sides are not perpendicular.
29. R(0, 0), S(6, 3), T(4, 7), V(2, 4) Yes, opp. sides are parallel and diag. are congruent.
454 Chapter 8 Quadrilaterals
454
Chapter 8 Quadrilaterals
Chapter 8 Study Guide and Review
Study Guide and Review
8-5 Rhombi and Squares
See pages
431–437.
Example
Concept Summary
• A rhombus is a quadrilateral with each side congruent, diagonals that are
perpendicular, and each diagonal bisecting a pair of opposite angles.
• A quadrilateral that is both a rhombus and a rectangle is a square.
Use rhombus JKLM to find mJMK and mKJM.
The opposite sides of a rhombus are parallel,
so KL
JM
. JMK LKM because
alternate interior angles are congruent.
mJMK mLKM
28
K
L
28˚
J
Definition of congruence
M
Substitution
The diagonals of a rhombus bisect the angles, so JKM LKM.
mKJM mJKL 180 Cons. in are suppl.
mKJM (mJKM mLKM) 180
mKJM (28 28) 180
mKJM 56 180
mKJM 124
mJKL mJKM mLKM
Substitution
Add.
Subtract 56 from each side.
Exercises Use rhombus ABCD with m1 2x 20, m2 5x 4,
AC 15, and m3 y 2 26. See Example 2 on page 432.
30. Find x. 8
31. Find AF. 7.5
32. Find y. 8 or 8
B
A
2
5
1
3
4
F
6
C
D
8-6 Trapezoids
See pages
439–445.
Example
Concept Summary
• In an isosceles trapezoid, both pairs of base angles are congruent and the
diagonals are congruent.
• The median of a trapezoid is parallel to the bases, and its measure is
one-half the sum of the measures of the bases.
ST
RSTV is a trapezoid with bases R
V
and and median M
N
.
Find x if MN 60, ST 4x 1, and RV 6x 11.
1
2
1
60 [(4x 1) (6x 11)]
2
MN (ST RV)
120 4x 1 6x 11
120 10x 10
110 10x
11 x
R
V
M
S
N
T
Substitution
Multiply each side by 2.
Simplify.
Subtract 10 from each side.
Divide each side by 10.
Chapter 8 Study Guide and Review 455
Chapter 8 Study Guide and Review 455
Study Guide and Review
Chapter 8 Study Guide and Review
Exercises
Answers
Find the missing value for the given trapezoid.
See Example 4 on page 441.
33. For isosceles trapezoid ABCD,
X and Y are midpoints of the legs.
Find mXBC if mADY 78. 102
35. Given: ABCD is a square.
Prove: A
C
⊥
BD
y
D(0, a)
B
C(a, a)
C
X
a0
a0
Slope of BD or 1
0a
The slope of AC
is the negative
reciprocal of the slope of BD
.
Therefore, A
C
⊥
BD
.
36. Given: ABCD is a parallelogram.
Prove: ABC CDA
y
D(b, c)
C (a b, c)
21
K
Y
L
57
A
B
78˚
O A(0, 0) B(a, 0) x
Proof:
a0
Slope of AC
or 1
34. For trapezoid JKLM, A and B are
midpoints of the legs. If AB 57
and KL 21, find JM. 93
A
D
J
M
8-7 Coordinate Proof with Quadrilaterals
See pages
447–451.
Example
Concept Summary
• Position a quadrilateral so that a vertex is at the origin and at least one
side lies along an axis.
Position and label rhombus RSTV on the coordinate plane. Then write a
coordinate proof to prove that each pair of opposite sides is parallel.
First, draw rhombus RSTV on the coordinate plane.
y
V (b, c)
T (a b, c)
Label the coordinates of the vertices.
Given: RSTV is a rhombus.
ST
VT
RS
Prove: RV
, O R (0, 0)
Proof:
O A(0, 0) B(a, 0)
x
Proof:
(a 0
)2 (0
0)2
AB a2 02 or a
DC [(a b
) b]2
(c c)2
a2 02 or a
AD (b 0
)2 (c
0)2
b2 c2
BC [(a b
) a]2
(c 0)2
b2 c2
AB and DC have the same measure,
so AB
DC
. AD and BC have the
same measure, so A
D
BC
.
A
C
A
C by the Reflexive Property.
Therefore, ABC CDA by SSS.
c0
c
b0
b
00
slope of RS
or 0
a0
slope of RV
or c0
c
(a b) a
b
cc
slope of VT
or 0
(a b) b
ST
R
RV
V
and S
T
have the same slope. So . R
S
and V
T
have the same slope,
VT
and R
S
.
Exercises Position and label each figure on the coordinate plane. Then write a
coordinate proof for each of the following. See Example 3 on pages 448 and 449.
35. The diagonals of a square are perpendicular. 35– 36. See margin.
36. A diagonal separates a parallelogram into two congruent triangles.
Name the missing coordinates for each quadrilateral.
y
37.
P(3a, c)
38.
456
Chapter 8 Quadrilaterals
See Example 2 on page 448.
O M (0, 0) N(4a, 0)x
456 Chapter 8 Quadrilaterals
U(a b, c)
y
T (0, c) U (?, ?)
R(a, c) P (?, ?)
4. FG
; opp. sides of are .
5. HGJ; alt. int. s are .
6. FGH; opp. s of are .
7. FK
; opp. sides of are ||.
14. Rectangle, rhombus, square; all sides are , cons. sides are ⊥.
15. Rhombus; all sides are , diag. are ⊥.
3.
x
slope of S
T
or Answers (page 457)
2.
S (a, 0)
W (a, 0)O
V (b, 0) x
Practice Test
Vocabulary and Concepts
Assessment Options
Determine whether each conditional is true or false. If false, draw a
counterexample.
1. If a quadrilateral has four right angles, then it is a rectangle. true
2. If a quadrilateral has all four sides congruent, then it is a square. False; see margin.
3. If the diagonals of a quadrilateral are perpendicular, then it is a rhombus. False; see margin.
Vocabulary Test A vocabulary
test/review for Chapter 8 can be
found on p. 472 of the Chapter 8
Resource Masters.
Skills and Applications
Complete each statement about FGHK. Justify your answer. 4–7. See margin.
4. H
K ? .
5. FKJ ? .
6. FKH ?
7. GH
.
?
F
G
J
.
K
Determine whether the figure with the given vertices is a parallelogram.
Justify your answer. 8. Yes, diag. bisect each other. 9. Yes, opp. sides are and .
8. A(4, 3), B(6, 0), C(4, 8), D(2, 5)
9. S(2, 6), T(2, 11), V(3, 8), W(1, 3)
10. F(7, 3), G(4, 2), H(6, 4), J(12, 2)
H
11. W(4, 2), X(3, 6), Y(2, 7), Z(1, 3)
No, opp. sides are not .
Yes, both pairs of opp. sides are .
ALGEBRA QRST is a rectangle.
12. If QP 3x 11 and PS 4x 8, find QS. 40
Q
R
P
13. If mQTR 2x2 7 and mSRT x2 18, find mQTR. 43
T
S
COORDINATE GEOMETRY Determine whether ABCD is a rhombus, a
rectangle, or a square. List all that apply. Explain your reasoning. 14–15. See margin.
14. A(12, 0), B(6, 6), C(0, 0), D(6, 6)
15. A(2, 4), B(5, 6), C(12, 4), D(5, 2)
Name the missing coordinates for each quadrilateral.
y
P(a b, c)
17.
16.
N (0, c)
M (a, 0) O
P (?, ?)
y
D (?, ?)
C (?, ?)
Sample answer:
C(a b, c), D(b, c)
A(0, 0)
Q (b, 0) x
O
Chapter Tests There are six
Chapter 8 Tests and an OpenEnded Assessment task available
in the Chapter 8 Resource Masters.
Form
1
2A
2B
2C
2D
3
Chapter 8 Tests
Type
Level
MC
MC
MC
FR
FR
FR
basic
average
average
average
average
advanced
Pages
459–460
461–462
463–464
465–466
467–468
469–470
MC = multiple-choice questions
FR = free-response questions
Open-Ended Assessment
Performance tasks for Chapter 8
can be found on p. 471 of the
Chapter 8 Resource Masters. A
sample scoring rubric for these
tasks appears on p. A28.
B (a 2b, 0) x
18. Position and label a trapezoid on the coordinate plane. Write a
coordinate proof to prove that the median is parallel to each base. See p. 459F.
19. SAILING Many large sailboats have a keel to keep the boat stable in
high winds. A keel is shaped like a trapezoid with its top and bottom
parallel. If the root chord is 9.8 feet and the tip chord is 7.4 feet, find
the length of the mid-chord. 8.6 ft
20. STANDARDIZED TEST PRACTICE The measure of an interior angle of a
regular polygon is 108. Find the number of sides. C
A 8
B 6
C 5
D 3
www.geometryonline.com/chapter_test
ExamView® Pro
Root chord
Mid-chord
Tip chord
Chapter 8 Practice Test 457
Portfolio Suggestion
Introduction Rectangles, parallelograms, and other shapes are used in
architecture.
Ask Students Ask students to design the façade of a house that incorporates
as many of the shapes and concepts from this chapter as possible. For each
shape, have students write a sentence describing a feature of the shape that is
useful in this context. Have students add their designs and descriptions to their
portfolios.
Use the networkable
ExamView® Pro to:
• Create multiple versions of
tests.
• Create modified tests for
Inclusion students.
• Edit existing questions and
add your own questions.
• Use built-in state curriculum
correlations to create tests
aligned with state standards.
• Apply art to your tests from a
program bank of artwork.
Chapter 8 Practice Test 457
Standardized
Test Practice
These two pages contain practice
questions in the various formats
that can be found on the most
frequently given standardized
tests.
Part 1 Multiple Choice
Record your answers on the answer sheet
provided by your teacher or on a sheet of
paper.
1. A trucking company wants to purchase a
ramp to use when loading heavy objects onto
a truck. The closest that the truck can get to
the loading area is 5 meters. The height from
the ground to the bed of the truck is 3 meters.
To the nearest meter, what should the length
of the ramp be? (Lesson 1-3) C
A practice answer sheet for these
two pages can be found on p. A1
of the Chapter 8 Resource Masters.
NAME
DATE
PERIOD
Practice
8Standardized
Standardized Test
Test Practice
Student Record
Sheet (Use with Sheet,
pages 458–459 of
Student
Recording
p.the Student
A1 Edition.)
Part 1 Multiple Choice
A
B
C
D
4
A
B
C
D
2
A
B
C
D
5
A
B
C
D
3
A
B
C
D
6
A
B
C
D
7
A
B
C
Part 2 Short Response/Grid In
For Question 11, also enter your answer by writing each number or symbol in a
box. Then fill in the corresponding oval for that number or symbol.
11
10
11
(grid in)
.
/
.
/
.
.
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
Part 3 Extended Response
4m
C
6m
See pp. 477–478 in the Chapter 8
Resource Masters for additional
standardized test practice.
122 ft
C
123 ft
D
20 ft
A
5. In rectangle JKLM shown below, JL
and M
K
are diagonals. If JL 2x 5 and
KM4x 11, what is x? (Lesson 8-4) B
A
10
8
6
B
5m
D
5
D
7m
If an astronaut is weightless, then he or
she is in orbit.
B
If an astronaut is not in orbit, then he or
she is not weightless.
C
If an astronaut is on Earth, then he or she
is weightless.
D
If an astronaut is not weightless, then he
or she is not in orbit.
M
B
L
N
J
K
6. Joaquin bought a set of stencils for his younger
sister. One of the stencils is a quadrilateral
with perpendicular diagonals that bisect each
other, but are not congruent. What kind of
quadrilateral is this piece? (Lesson 8-5) C
A
square
B
rectangle
C
rhombus
D
trapezoid
7. In the diagram below, ABCD is a trapezoid
with diagonals A
C
and B
D
intersecting at
point E.
A
B
E
3. Rectangle QRST measures 7 centimeters
long and 4 centimeters wide. Which of the
following could be the dimensions of a
rectangle similar to rectangle QRST?
(Lesson 6-2)
24 ft
60˚
B
D
C
Which statement is true? (Lesson 8-6) A
A
28 cm by 14 cm
A
A
B is parallel to C
D
.
B
21 cm by 12 cm
B
ADC is congruent to BCD.
C
14 cm by 4 cm
C
DE
CE
is congruent to .
D
7 cm by 8 cm
D
AC
and B
D
bisect each other.
458 Chapter 8 Quadrilaterals
ExamView® Pro
Special banks of standardized test
questions similar to those on the SAT,
ACT, TIMSS 8, NAEP 8, and state
proficiency tests can be found on this
CD-ROM.
458 Chapter 8 Quadrilaterals
12 ft
B
C
If an astronaut is in orbit, then he or she is
weightless.
Record your answers for Questions 12–13 on the back of this paper.
Additional Practice
A
5m
2. Which of the following is the contrapositive
of the statement below? (Lesson 2-3) D
Answers
9
A
C
New SE page
to come
D
Solve the problem and write your answer in the blank.
8
(Lesson 7-3)
3m
Select the best answer from the choices given and fill in the corresponding oval.
1
4. A 24 foot ladder, leaning against a house,
forms a 60° angle with the ground. How far
up the side of the house does the ladder reach?
Preparing for Standardized Tests
For test-taking strategies and more
practice, see pages 795– 810.
Evaluating Extended
Response Questions
Part 2 Short Response/Grid In
Record your answers on the answer sheet
provided by your teacher or on a sheet of
paper.
8. At what point does the graph of
y 4x 5 cross the x-axis on a
5
coordinate plane? (Prerequisite Skill) , 0
4
9. Candace and Julio are planning to see a
movie together. They decide to meet at the
house that is closer to the theater. From the
locations shown on the diagram, whose
house is closer to the theater? (Lesson 5-3)
Julio’s house
Theatre
85˚
40˚
Candace
55˚
Test-Taking Tip
Question 10
Read the question carefully to check that you answered the
question that was asked. In question 10, you are asked to
write an equation, not to find the length of the mast.
Part 3 Extended Response
Record your answers on a sheet of paper.
Show your work.
12. On the tenth hole of a golf course, a sand
trap is located right before the green at
point M. Matt is standing 126 yards away
from the green at point N. Quintashia is
standing 120 yards away from the beginning
of the sand trap at point Q.
Julio
M a
P
10. In the diagram, CE
is the mast of a sailboat
with sail ABC.
126 yd
N
C
120 yd
Extended Response questions
are graded by using a multilevel
rubric that guides you in
assessing a student’s knowledge
of a particular concept.
Goal: In Exercise 12, students use
properties to find a distance. In
Exercise 13, students use a
coordinate proof to draw
conclusions about a quadrilateral.
Sample Scoring Rubric: The
following rubric is a sample
scoring device. You may wish to
add more detail to this sample to
meet your individual scoring
needs.
400 yd
Q
R
Score
Criteria
4
A correct solution that is
supported by well-developed,
accurate explanations
A generally correct solution,
but may contain minor flaws
in reasoning or computation
A partially correct interpretation
and/or solution to the problem
A correct solution with no
supporting evidence or
explanation
An incorrect solution indicating
no mathematical understanding
of the concept or task, or no
solution is given
a. Explain why MNR is similar to PQR.
(Lesson 6-3)
See margin.
3
A
4 ft
D
4 ft
E
B
25 ft
Marcia wants to calculate the length, in
feet, of the mast. Write an equation in which
the geometric mean is represented by x.
(Lesson 7-1) 4
x
x 25
11. AC
is a diagonal of rhombus ABCD.
If mCDE is 116, what is mACD?
(Lesson 8-4)
58
B
13. Quadrilateral ABCD has vertices with
coordinates: A(0, 0), B(a, 0), C(ab, c),
and D(b, c).
a. Position and label ABCD on the
coordinate plane. Prove that ABCD
is a parallelogram. (Lesson 8-2 and 8-7)
See p. 459F.
b. If a2 b 2 c 2, what can you determine
about the slopes of the diagonals A
C
and B
D
? (Lesson 8-7) See p. 459F.
C
c. What kind of parallelogram is ABCD?
116˚
A
b. Write and solve a proportion to find
the distance across the sand trap, a.
(Lesson 6-3) 400 a
400
; a 20 yd
126
120
D
E
www.geometryonline.com/standardized_test
Since the diagonals are
perpendicular, ABCD is a rhombus.
(Lesson 8-7)
Chapter 8 Standardized Test Practice 459
2
1
0
Answers
12a. MNR and PQR are both right
angles and all right angles are
congruent, so MNR PQR.
Since congruence of angles is
reflexive, R R. MNR
is similar to PQR because
two angles are congruent
(AA Similarity).
Chapter 8 Standardized Test Practice 459
Pages 407–409, Lesson 8-1
3. Sample answer: regular quadrilateral, 360°
42. Given: GKLM
Prove: G and K are supplementary.
K and L are supplementary.
L and M are supplementary.
M and G are supplementary.
;
quadrilateral that is not regular, 360°
G
M
57. Given: JL
|| K
M
, JK
|| L
M
Prove: JKL MLK
J
K
Proof:
Statements (Reasons)
L
M
Additional Answers for Chapter 8
1. JL
|| K
M
, JK
|| L
M
(Given)
2. MKL JLK, JKL MLK (Alt. int. s are .)
3. KL
K
L
(Reflexive Property)
4. JKL MLK (ASA)
Pages 414–416, Lesson 8-2
13. Given: VZRQ and WQST
Prove: Z T
Q
R
S
W
T
V
Proof:
Z
Statements (Reasons)
1. VZRQ and WQST (Given)
2. Z Q, Q T (Opp. s of a are .)
3. Z T (Transitive Prop.)
14. Given: XYRZ, WZ
WS
W
Prove: XYR S
Y
X
Proof: Opposite angles of a
parallelogram are congruent, so
Z
R
S
Z XYR. By the Isosceles Triangle
Theorem, since WZ
WS
, Z S.
By the Transitive Property, XYR S.
40. They are all congruent parallelograms. Since A, B and C
are midpoints, AC
, AB
, and B
C
are midsegments. The
midsegment is parallel to the third side and equal to half
the length of the third side. So, each pair of opposite
sides of ACBX, ABYC, and ABCZ are parallel.
41. Given: PQRS
P
Q
1 3
Prove: P
Q
RS
4 2
R
Q
SP
S
R
Proof:
Statements (Reasons)
1. PQRS (Given)
2. Draw an auxiliary segment PR
and label angles 1,
2, 3, and 4 as shown. (Diagonal of PQRS)
3. PQ
|| S
R
, PS
|| Q
R
(Opp. sides of are ||.)
4. 1 2, and 3 4 (Alt. int. s are .)
5. PR
P
R
(Reflexive Prop.)
6. QPR SRP (ASA)
7. PQ
RS
and QR
SP
(CPCTC)
459A
Chapter 8 Additional Answers
K
L
Proof:
Statements (Reasons)
1. GKLM (Given)
2. GK
|| M
L
, GM
|| K
L (Opp. sides of are ||.)
3. G and K are supplementary, K and L are
supplementary, L and M are supplementary,
M and G are supplementary. (Cons. int. are
suppl.)
43. Given: MNPQ
M
N
M is a right angle.
Prove: N, P and Q are right
Q
P
angles.
Proof: By definition of a parallelogram, MN
|| Q
P
.
Since M is a right angle, MQ
⊥
MN
. By the
Perpendicular Transversal Theorem, MQ
⊥
QP
. Q is
a right angle, because perpendicular lines form a right
angle. N Q and M P because opposite
angles in a parallelogram are congruent. P and N
are right angles, since all right angles are congruent.
44. Given: ACDE is a parallellogram.
A
C
B
Prove: EC
bisects AD
.
A
D
bisects EC
.
E
D
Proof: It is given that ACDE is a parallelogram. Since
opposite sides of a parallelogram are congruent,
E
A
. By definition of a parallelogram, EA
|| D
C
.
DC
AEB DCB and EAB CDB because
alternate interior angles are congruent. EBA CBD by ASA. EB
B
C
and A
B
BD
by CPCTC.
By the definition of segment bisector, E
C
bisects
D
A
and A
D
bisects E
C
.
45. Given: WXYZ
W
X
Prove: WXZ YZX
Proof:
Z
Y
Statements (Reasons)
1. WXYZ (Given)
2. WX
Z
Y
, WZ
XY
(Opp. sides of are .)
3. ZWX XYZ (Opp. of are .)
4. WXZ YZX (SAS)
Pages 420–423, Lesson 8-3
11. Given: PT
T
R
TSP TQR
Prove: PQRS is a
S
parallelogram.
P
Q
T
R
Proof:
Statements (Reasons)
1. PT
, TSP TQR (Given)
TR
2. PTS RTQ (Vertical are .)
3. PTS RTQ (AAS)
4. PS
QR
(CPCTC)
5. P
S
|| Q
R
(If alt. int. are , lines are ||.)
6. PQRS is a parallelogram. (If one pair of opp. sides
is || and , then the quad. is a .)
39. Given: AD
BC
A
B
3
2
B
A
DC
1
4
Prove: ABCD is a parallelogram.
D
C
Proof:
Statements (Reasons)
4
Proof:
Statements (Reasons)
D
C
1. AE
, DE
E
B
(Given)
EC
2. 1 2, 3 4 (Vertical are .)
3. ABE CDE, ADE CBE (SAS)
4. AB
DC
, AD
B
C
(CPCTC)
5. ABCD is a parallelogram. (If both pairs of opp. sides
are , then quad is a .)
41. Given: AB
DC
A
B
1
B
A
|| D
C
2
Prove: ABCD is a parallelogram.
D
C
Proof:
Statements (Reasons)
1. AB
DC
, AB
|| D
C
(Given)
2. Draw AC
(Two points determine a line.)
3. 1 2 (If two lines are ||, then alt. int. are .)
4. AC
A
C
(Reflexive Property)
5. ABC CDA (SAS)
6. AD
B
C
(CPCTC)
7. ABCD is a parallelogram. (If both pairs of opp. sides
are , then the quad. is .)
Q
R
S
Proof:
Statements (Reasons)
P
V
T
1. PQST is a rectangle; QR
VT
. (Given)
2. PQST is a parallelogram. (Def. of rectangle)
3. TS
PQ
(Opp. sides of are .)
4. T and Q are rt. . (Definition of rectangle)
5. T Q (All rt. are .)
6. RPQ VST (SAS)
7. PR
V
S
(CPCTC)
43. Given: DEAC and FEAB are
N
rectangles.
MA
E
GKH JHK
F
GJ and HK
intersect at L. B C
D
G
K
Prove: GHJK is a parallelogram.
J
H
L
Proof:
Statements (Reasons)
1. DEAC and FEAB are rectangles; GKH JHK;
GJ and HK
intersect at L. (Given)
2. D
E
|| A
C
and FE
|| A
B
(Def. of parallelogram)
||
3. plane N plane M (Def. of parallel plane)
4. G, J, H, K, L are in the same plane. (Def. of
intersecting lines)
5. GH
|| K
J (Def. of parallel lines)
6. GK
|| H
J (Alt. int. s are )
7. GHJK is a parallelogram. (Def. of parallelogram)
Pages 434–437, Lesson 8-5
10. Given: KGH, HJK, GHJ,
and JKG are isosceles.
Prove: GHJK is a rhombus.
G
H
Proof:
K
J
Statements (Reasons)
1. KGH, HJK, GHJ, and JKG are isosceles.
(Given)
2. KG
GH
, HJ KJ, GH
HJ, KG
KJ (Def. of
isosceles )
3. KG
HJ, GH
K
J (Transitive Property)
4. KG
, HJ K
J (Substitution)
GH
5. GHJK is a rhombus. (Def. of rhombus)
Chapter 8 Additional Answers 459B
Additional Answers for Chapter 8
1. AD
B
C
, AB
D
C
(Given)
2. Draw D
B
. (Two points determine a line.)
3. DB
D
B
(Reflexive Property)
4. ABD CDB (SSS)
5. 1 2, 3 4 (CPCTC)
6. AD
|| B
C
, AB
|| D
C
(If alt. int. are , lines are ||.)
7. ABCD is a parallelogram. (Def. of parallelogram)
40. Given: AE
EC
, DE
EB
A
B
E
3
Prove: ABCD is a parallelogram.
1
2
Pages 427–430, Lesson 8-4
42. Given: PQST is a rectangle.
Q
R
VT
Prove: PR
VS
Additional Answers for Chapter 8
35. Given: ABCD is a parallelogram.
A
B
C
A
⊥
BD
E
Prove: ABCD is a rhombus.
Proof: We are given that ABCD is a
parallelogram. The diagonals of a
D
C
parallelogram bisect each other, so
AE
EC
. BE
BE
because congruence of segments
is reflexive. We are also given that A
C
⊥
BD
. Thus,
AEB and BEC are right angles by the definition of
perpendicular lines. Then AEB BEC because all
right angles are congruent. Therefore, AEB CEB
by SAS. AB
C
B
by CPCTC. Opposite sides of
parallelograms are congruent, so A
B
CD
and
BC
AD
. Then since congruence of segments is
transitive, A
B
C
D
BC
AD
. All four sides of
ABCD are congruent, so ABCD is a rhombus by
definition.
36. Given: ABCD is a rhombus.
A
B
6
3
Prove: Each diagonal bisects a pair
4
5
of opposite angles.
1 2 7 8
Proof: We are given that ABCD is a
rhombus. By definition of rhombus,
D
C
ABCD is a parallelogram. Opposite
angles of a parallelogram are congruent,
so ABC ADC and BAD BCD.
AB
BC
C
D
DA
because all sides of a rhombus
are congruent. ABC ADC by SAS. 5 6 and
7 8 by CPCTC. BAD BCD by SAS.
1 2 and 3 4 by CPCTC. By definition of
angle bisector, each diagonal bisects a pair of
opposite angles.
3. Sample answer: The median of a trapezoid is parallel
to both bases.
trapezoid
isosceles trapezoid
6. Given: CDFG is an isosceles
and GF
.
trapezoid with bases CD
Prove: DGF CFG
Proof:
CDFG is an isosceles
trapezoid with
bases CD and GF.
D
C
G
F
CG DF
Def. isos. trap.
Given
CF DG
GF GF
Diag. of isos.
trap. are .
Reflex. Prop.
CGF DFG
SSS
DGF CFG
CPCTC
32. Given: H
J || G
K
, H
G ||⁄ JK,
HGK JKG
Prove: GHJK is an isosceles
trapezoid.
Proof:
HJ GK,
HG JK
H
J
K
G
HGK JKG
Given
Given
Page 438, Geometry Activity
5.
The diagonals intersect in a right angle;
J
JKL JML; KP
PM
, JP
PL
;
K
3
pairs:
JPK
JPM,
KPL
M
P
MPL, JKL JML.
Def. of trapezoid
HG JK
CPCTC
GHJK is an isosceles trapezoid.
Def. of isosceles trapezoid
L
6. One pair of opposite angles is congruent. The
diagonals are perpendicular. The longer diagonal
bisects the shorter diagonal. The short sides are
congruent and the long sides are congruent.
Pages 442–445, Lesson 8-6
2. Properties
Trapezoid Rectangle
459C
GHJK is a trapezoid.
TZX YXZ
Given
1 2
Square Rhombus
diagonals are
congruent
only
isosceles
yes
yes
no
diagonals are
perpendicular
no
no
yes
yes
diagonals bisect
each other
no
yes
yes
yes
diagonals bisect
angles
no
no
yes
yes
Chapter 8 Additional Answers
33. Given: TZX YXZ, W
X ||⁄ ZY
Prove: XYZW is a trapezoid.
Proof:
CPCTC
WZ || XY
If alt. int. are , then the
lines are ||.
WX || ZY
XYZW is a trapezoid.
Given
Def. of trapezoid
T W 1 Z
X
2
Y
34. Given: ZYXP is an isosceles trapezoid.
Prove: PWX is isosceles.
Proof:
X
Y
W
P
Z
ZYXP is an isosceles trapezoid.
WY WZ
Base of an
isos. trap. are .
WX XY WY,
WP PZ WZ
WY WZ
Def. of
isos. trap.
WX WP
Substitution
Subtraction
PWX is isosceles.
WX WP
Def. of isos. Def. of 1 3
2
4
A
EC || AB
B
O
E(765, 180)
G(195, 0)
F(533, 0)
x
Proof:
180 180
Slope of D
E
or 0
12DB
Def. of Midpt.
765 195
00
Slope of G
F
or 0
533 195
AE BC
180 0
765 533
45
58
Slope of E
F
or AE BC
Def. of 180 0
195 195
Slope of D
G
or undefined
DE
and G
F
have the same slope, so exactly one pair
of opposite sides are parallel. Therefore, DEFG is a
trapezoid.
y
9.
10.
y
ABCE is an isos.
trapezoid.
Def. of isos. trapezoid
Pages 449–451, Lesson 8-7
1. Place one vertex at the origin and position the figure
so another vertex lies on the positive x-axis.
2. Sample answer:
3.
y
D (0, a b)
C (a, a b)
C (b, c)
B(b, a)
O A(0, 0)
B(a, 0) x
AD DB
Substitution
(0, d )
O A(0, 0)
y
D (195, 180)
1
2 AD
A segment joining the
midpoints of two sides
of a triangle is parallel
to the third side.
C (a, a)
The slope of A
C
is the negative reciprocal of the slope
of DB
, so they are perpendicular.
8. Given: D(195, 180), E(765, 180), F(533, 0), G(195, 0)
Prove: DEFG is a trapezoid.
C
Given
Given
y
D (0, a)
a0
0a
Slope of A
C or 1
0a
D
E
B(a, 0) x
x
O A(0, 0)
B(a, 0) x
D (b, c)
O A(0, 0)
C (a b, c)
D (a, b)
B(a 2b, 0) x
O A(0, 0)
C (c a, b)
B(c, 0) x
y
17. Given: ABCD is a rectangle.
A(0, b) B(a, b)
Prove: AC
DB
Proof: Use the Distance Formula
2 b2
to find AC a
and
O D(0, 0) C (a, 0) x
2
2
BD a b . AC
and
D
B
have the same length, so they are congruent.
Chapter 8 Additional Answers 459D
Additional Answers for Chapter 8
35. Given: E and C are midpoints
of AD
and DB
.
A
D
DB
Prove: ABCE is an isosceles
trapezoid.
Proof:
E and C are midpoints
of AD and DB.
C
A
and D
B
bisect each other.
7. Given: ABCD is a square.
Prove: AC
⊥
DB
Proof:
0a
Slope of D
B
or 1
Def. of WX XY WP PZ
C (a b, c)
2
2 ab c
, 2
2
ab 0c
The midpoint of DB
, 2
2
ab c
, 2
2
XY PZ
Def. of y
D (b, c)
O A(0, 0)
XY PZ
If 2 of a are , the sides
opp. are .
Segment
Addition
D
y
Proof:
0 (a b) 0 c
The midpoint of AC
, Given
Y Z
6. Given: ABCD is a parallelogram.
Prove: A
C
and D
B
bisect
each other.
18. Given: ABCD and AC
BD
Prove: ABCD is a rectangle.
Proof:
AC (a b
0)2
(c 0)2
y
D (b, c)
C (a b, c)
B(a, 0) x
O A(0, 0)
Additional Answers for Chapter 8
(b a
)2 (c
0)2
BD But AC BD and
(a b
0)2
(c 0)2 (b a
)2 (c
0)2
2
2
2
(a b 0) (c 0) (b a) (c 0)2
(a b)2 c2 (b a)2 c2
a2 2ab b2 c2 b2 2ab a2 c2
2ab 2ab
4ab 0
a 0 or b 0
Because A and B are different points, a 0. Then
b 0. The slope of A
D
is undefined and the slope of
AB
0. Thus AD
⊥
AB
. DAB is a right angle and
ABCD is a rectangle.
y
19. Given: isosceles trapezoid
D (b, c) C (a b, c)
ABCD with AD
B
C
Prove: BD
AC
B(a, 0) x
O A(0, 0)
Proof:
BD (a b
)2 (0
c)2 (a b
)2 c2
(a b
)2 c2
AC ((a b) (c
BD AC and BD
AC
y
20. Given: ABCD is an
isosceles trapezoid A(b, c)
with median XY
.
X
Y
|| A
B
and
Prove: X
O D(0, 0)
X
Y
|| D
C
0)2
0)2
B(a b, c)
Y
C (a, 0) x
2a b c
, . The
2b , 2c. The midpoint of BC is Y 2
2
slope of A
B
0, the slope of X
Y
0 and the slope of
D
C
0. Thus, XY
|| A
B
and XY
|| D
C
.
C(a, b)
R
S
B(a, 0) x
T
2 2 2
a0 bb
a 2b
a
Midpoint R is , or , or , b.
2
2
2 2
2
aa b0
2a b
b
Midpoint S is , or , or a, .
2
2
2 2
2
a0 00
a
Midpoint T is , or , 0.
2
2
2
a2 0 b b2 a2 b2
RS a a2 b2 b
a2 b2 or a2 b2
QR 2
459E
2
2
2
2
2
Chapter 8 Additional Answers
2
2
2
2
2
2
2
2
2
2
2
2
2
2
QR RS ST QT
R
Q
S
T
Q
T
RS
QRST is a rhombus.
22. Given: RSTV is a quadrilateral.
A, B, C, and D are midpoints of sides
RS
, ST
, TV
, and V
R
, respectively.
Prove: ABCD is a parallelogram.
y
T (2d, 2b)
S(2a, 2e)
B
C
A
O
D
R(0, 0)
V(2c, 0) x
Proof: Place quadrilateral RSTV on the coordinate
plane and label coordinates as shown. (Using
coordinates that are multiples of 2 will make the
computation easier.) By the Midpoint Formula, the
22a
2e
2
coordinates of A, B, C, and D are A , (a, e);
2d 2a
B ,
2
2d 2c
C ,
2
2e 2b
(d a, e b);
2
2b
2c 0
(d c, b); and D , (c, 0).
2
2 2
Find the slopes of A
B
and DC
.
Slope of A
B
Slope of D
C
y2 y1
m
x x
2
Proof: The midpoint of A
D
is X. The coordinates are
21. Given: ABCD is a rectangle.
y
D(0, b)
Q, R, S, and T are
midpoints of their
Q
O
respective sides.
A(0, 0)
Prove: QRST is a rhombus.
Proof:
00 b0
b
Midpoint Q is , or 0, .
a a2 b2 0 a2 b2
QT a2 0 0 b2
a2 b2 or a2 b2
ST 1
(e b) e
(d a) a
b
d
y2 y1
m
x x
2
1
0b
c (d c)
b
b
or d
d
The slopes of A
B
and D
C
are the same so the
segments are parallel.
Use the Distance Formula to find AB and DC.
AB ((d a) a
)2 ((
e b
) e)2
2
2
d
b
DC ((d c) c
)2 (b
0)2
2 b2
d
Thus, A
B
DC
. Therefore, ABCD is a parallelogram
because if one pair of opposite sides of a quadrilateral
are both parallel and congruent, then the quadrilateral
is a parallelogram.
Page 457, Chapter 8 Practice Test
18. Given: isosceles trapezoid WXYZ with median ST
Prove: WX
|| S
T
|| Y
Z
y
W(0, 2d )
S(a, d )
Z(2a, 0) O
Pages 458–459, Chapter 8 Standardized Test Practice
13a. Given: quadrilateral ABCD
y
D (b, c) C (a b, c)
Prove: ABCD is a
parallelogram
X(b, 2d)
T(a b, d )
Y(2a b, 0) x
Proof: To prove lines parallel, show their slopes equal.
2d 2d
The slope of WX is or 0.
b0
dd
The slope of ST is or 0.
(a b) (a)
00
The slope of YZ is or 0.
(2a b) (2a)
Since WX, ST, and YZ all have zero slope, they are
parallel.
O A(0, 0)
c0
b0
B(a, 0) x
c
b
Proof: The slope of A
D
is or . The slope of
c0
aba
c
b
BC
is or . AD
and BC
have the same
slope so they are parallel.
2 c2
AD (b 0
)2 (c
0)2 b
.
BC (a b
a)2
(c 0)2 b 2 c 2.
Since one pair of opposite sides are parallel and
congruent, ABCD is a parallelogram.
c0
ab0
c
ab
13b. The slope of A
C
is or . The slope of
c0
c
ba
ba
c
c
c2
. Since c 2 a 2 b 2, the
2
ab
ba
b a2
a2 b2
or 1, so the
product of the slopes is b2 a2
B
D
is or . The product of the slopes is
Chapter 8 Additional Answers 459F
Additional Answers for Chapter 8
diagonals of ABCD are perpendicular.